|
|
|
发布时间: 2019-10-10 |
|
|
|
|
收稿日期: 2019-03-01
基金项目: 上海市科学技术委员会地方能力建设项目(18020500900);上海市自然科学基金(19ZR1420700);上海市电站自动化技术重点实验室项目(13DZ2273800)
中图法分类号: TM623
文献标识码: A
文章编号: 1006-4729(2019)05-0405-08
|
摘要
核电站凝汽器的健康度评价对设备运行维护具有重要的指导意义。提出了一种变权重模糊健康度评价方法。首先, 通过数据机理得到相关的评价参数集, 以评价参数作为失效依据, 利用隶属度函数对每个评价参数进行状态评分, 再利用状态评分计算参数集的模糊关系矩阵; 然后, 利用熵值法确定评价参数常权重系数, 在此基础上, 引入基于均衡函数的变权公式, 结合变权重矩阵和模糊关系矩阵进行模糊综合评判; 最后, 得到了其综合健康度。利用该方法对凝汽器进行了健康度评价, 结果表明, 当设备运行进入异常状态时, 可实现对故障的早期预报, 提高了核电站凝汽器运行的安全性与可靠性。
关键词
机理模型; 凝汽器; 变权重; 健康度评价
Abstract
The health evaluation of condenser in the nuclear power plant has important significance for the operation and maintenance of the equipment.A variable weight fuzzy health evaluation method is proposed.Firstly, the relevant evaluation parameter set is obtained through the data mechanism.Using the evaluation parameter as the failure criterion, the status of each evaluation parameter is firstly scored by using the membership function, and the fuzzy relation matrix of the parameter set is calculated by using the state score; then, the entropy method is used to determine the correlation parameter set.Based on the constant weights of the evaluation parameters, a variable weight formula based on the equalization function is introduced.Then the variable weight matrix and the fuzzy relation matrix are used for fuzzy comprehensive evaluation.And finally the comprehensive health degree is obtained.Using the method proposed to evaluate the health of the condenser, the results show that when the equipment is running into an abnormal state, it can realize early detection.This method improves the safety and reliability of condenser operation in nuclear power plants.
Key words
mechanism model; condenser; variable weight; health evaluation
凝汽器是核电站常规岛部分的重要换热设备, 能否正常运行直接影响整个汽轮机组运行安全和热经济效益。由于凝汽器结构较为复杂, 各参数间的耦合性也相对较强, 其多数故障诊断系统只能诊断出较严重的故障, 对故障早期的异常很难做出判断。因此, 有必要对凝汽器进行健康度评价的研究, 实现对故障的早期预警, 从而避免和减轻严重的设备损坏, 降低运行与维护费用, 提高凝汽系统运行的安全性和可靠性。健康度是通过综合分析凝汽系统设备运行中各种状态信息和现场设备的运行工况得到的单一数值。其值是对凝汽器健康状态的综合度量。
目前, 国内外关于设备健康度评价与预测的方法很多。文献[1]基于模糊集的数据融合方法对多数据进行融合计算得到了系统的健康度; 文献[2]提出了一种基于Dezert-Smarandache理论(DSmT)和模糊综合评判的健康状态评估模型; 文献[3]通过模糊数学和层次分析法对变压器的健康状态进行了评估; 文献[4]将退化隐式半马尔科夫模型用于诊断设备健康状态和预测有效剩余寿命; 文献[5]采用基于监测参数的专家系统的方法对设备的健康度进行了评估; 文献[6]提出了一种基于粗糙核距离度量的健康状态评估方法; 文献[7]提出了一种基于相似性度量的健康评估的变精度粗集决策方法。但以上健康状态评估方法中评估参数大多根据专家经验选自实时参数中的一部分参数, 具有一定的主观性, 不能保证这样的评估参数能快速准确地反映设备的运行状态。
本文从机理分析出发, 通过构建凝汽器的故障模型, 得到设备健康度评价参数集, 以理论分析选取合适的评价参数, 更加准确地反映凝汽器运行状态的健康程度。以评价参数作为失效依据, 首先计算各评价参数的阈值和限值, 然后利用引入均衡函数后的变权公式计算权重, 运用综合加权法建立单个设备多特征参数健康度评价模型, 实现对设备健康度的客观合理评价。
1 提取核电站凝汽器健康度评价参数
凝汽器的真空度是指汽轮机低压缸排汽端真空占当地大气压pdq的百分数, 能够间接反应凝汽器的运行状态, 其计算公式为
| $ \eta_{ \mathrm{zk}}=\left(1-\frac{p_{\mathrm{c}}}{p_{\mathrm{dq}}}\right) \times 100 \% $ | (1) |
式中:pc——凝汽器压力。
由于当地大气压一般趋于稳定, 可以通过凝汽器压力的变化来反应其运行状态。由于空气的漏入, 根据气体混合物的道尔顿分压定律, 混合物的总压力等于其各组成气体的分压力之和, 因此凝汽器压力公式[8]为
| $ \frac{\mathrm{d} p_{\mathrm{c}}}{\mathrm{d} \tau}=\frac{\mathrm{d} p_{\mathrm{s}}}{\mathrm{d} \tau}+\frac{\mathrm{d} p_{\mathrm{a}}}{\mathrm{d} \tau} $ | (2) |
式中:ps——蒸汽分压力;
pa——空气分压力。
低压蒸汽可视为理想气体, 根据蒸汽区凝汽器蒸汽质量平衡、理想气体状态方程, 微分得到凝汽器蒸汽分压力为
| $ \begin{aligned} \frac{\mathrm{d} p_{\mathrm{s}}}{\mathrm{d} \tau}=& \left[\left(F_{\mathrm{st}}+F_{\mathrm{si}}+F_{\mathrm{f}}+F_{\mathrm{v}}\right)\right.\\ & \left.-\left(F_{\mathrm{as}}+F_{\mathrm{c}}+F_{\mathrm{da}}+F_{\mathrm{ss}}+F_{\mathrm{rs}}\right)\right] \cdot \\ & \frac{R_{\mathrm{s}}\left(t_{\mathrm{v}}+273\right)}{V} \end{aligned} $ | (3) |
式中:Fst——汽轮机低压缸排汽量, kg/s;
Fsi——给水泵小汽机排入凝汽器的蒸汽量, kg/s;
Ff——凝汽器疏水闪蒸量, kg/s;
Fv——动态蒸发量, kg/s;
Fas——热井水面的动态凝结量, kg/s;
Fc——蒸汽主凝汽量, kg/s;
Fda——凝汽器向环境散热而折合的蒸汽凝结量, kg/s;
Fss——抽真空系统抽出的蒸汽量, kg/s;
Frs——超压装置动作时排出的蒸汽量, kg/s;
Rs——壳侧蒸汽的气体常数;
tv——蒸汽平均温度, ℃;
V——凝汽器内汽气空间体积, m3。
凝汽器中的空气类似蒸汽, 可视为理想气体, 根据进出凝汽器的空气量, 利用质量平衡原理可得
| $\frac{\mathrm{d} p_{\mathrm{a}}}{\mathrm{d} \tau}=\left[\left(F_{\mathrm{vb}}+F_{\mathrm{n}}+F_{\mathrm{g}}+F_{\mathrm{r}}\right)-\right. \\ \left.\left(F_{\mathrm{ao}} R+F_{\mathrm{R}} R\right)\right] \cdot \frac{R_{\mathrm{a}}\left(t_{\mathrm{a}}+273\right)}{V}$ | (4) |
式中:Fvb——真空破坏阀进入凝汽器的空气量, kg/s;
Fn——正常漏入凝汽器的空气量, kg/s;
Fg——由轴封漏入凝汽器的空气量, kg/s;
Fr——故障时漏入凝汽器的空气量, kg/s;
Fao——抽真空设备抽出的混合气体量, kg/s;
R——凝汽器内空气质量份额;
FR——超压排气量, kg/s;
Ra——空气气体常数;
ta——空气平均温度。
当tc > tr时,
| $ \left\{\begin{array}{l} F_{\mathrm{as}}=k_{\mathrm{as}} \cdot\left(t_{\mathrm{c}}-t_{\mathrm{r}}\right) \\ F_{\mathrm{v}}=0 \end{array}\right. $ | (5) |
当tc < tr时
| $ \left\{\begin{array}{l} F_{\mathrm{as}}=0 \\ F_{\mathrm{v}}=k_{\mathrm{v}} \cdot\left(t_{\mathrm{r}}-t_{\mathrm{c}}\right) \end{array}\right. $ | (6) |
| $ \begin{aligned} \mathrm{F}_{c}=& \frac{\mathrm{KA}_{n} \Delta \mathrm{t}_{m}}{\mathrm{H}_{s}-\mathrm{H}_{c w}}=\frac{\mathrm{K} \mathrm{A}_{n}}{\mathrm{H}_{s}-\mathrm{H}_{c w}} \cdot \\ & \frac{\Delta \mathrm{t}}{\ln \left[\frac{\Delta \mathrm{t}+\delta_{t}}{\delta_{t}}\right]}\end{aligned} $ | (7) |
| $A_{\mathrm{n}}=A \cdot \frac{h_{\mathrm{t}}-h_{\mathrm{h}}}{h_{\mathrm{t}}-h_{\mathrm{b}}}$ | (8) |
式中:kas——蒸汽动态凝结系数, kg/(s·℃);
tc——凝汽器蒸汽分压力对应的饱和温度, ℃;
tr——热井水温, ℃;
kv——热井水动态蒸发系数, kg/(s·℃);
K——凝汽器的换热系数, W/(m2·℃);
An——凝汽器传热面积, m2;
Δtm——凝结水温度的变化量, ℃;
Hs——凝汽器内蒸汽的汽焓, kJ/kg;
Hcw——饱和压力下对应的水焓, kJ/kg;
Δt——循环水温升, ℃;
δt——凝汽器端差, ℃;
A——凝汽器总换热面积, m2;
ht——冷却水管最上排管束至热井底部的距离, m;
hh——热井水实际水位, m;
hb——冷却水管最上排管束至热井底部的距离, m。
在凝汽器压力下的饱和温度ts与凝结水温度tm之差称为凝结水的过冷却度, 其公式如下
| $\Delta t_{\mathrm{n}}=t_{\mathrm{s}}-t_{\mathrm{m}}$ | (9) |
通过对凝汽器压力机理模型的分析, 并综合式(2)~式(8), 可将基于凝汽压力的机理模型描述为
| $p_{\mathrm{c}}=f_{1}\left(\Delta t, \delta_{\mathrm{t}}, t_{\mathrm{r}}, h_{\mathrm{h}}, \Delta t_{\mathrm{n}}\right)$ | (10) |
式(10)中循环水温升Δt、凝汽器端差δt、热井水温tr、热井水实际水位hh、凝结水的过冷却度Δtn分别为凝汽器压力机理模型中的影响因素, 因此选择pc, Δt, δt, tr, hh, Δtn作为凝汽器健康度评价的主要评价参数。分别对式(10)中的自变量求偏导数, 得到凝汽器压力下的故障模型如下(其中μ1, μ2, μ3, μ4, μ5为常数)
| $ \begin{aligned} \Delta p_{c}=& \mu_{1} \Delta(\Delta t)+\mu_{2} \Delta\left(\delta_{\mathrm{t}}\right)+\mu_{3} \Delta t_{\mathrm{r}}+\\ & \mu_{4} \Delta h_{\mathrm{h}}+\Delta\left(\Delta t_{\mathrm{n}}\right) \end{aligned} $ | (11) |
| $\mu_{1}=\frac{\partial f_{1}\left(\Delta t, \delta_{\mathrm{t}}, t_{\mathrm{r}}, h_{\mathrm{h}}, \Delta t_{\mathrm{n}}\right)}{\partial(\Delta t)}$ | (12) |
| $\mu_{2}=\frac{\partial f_{1}\left(\Delta t, \delta_{\mathrm{t}}, t_{\mathrm{r}}, h_{\mathrm{h}}, \Delta t_{\mathrm{n}}\right)}{\partial \delta_{\mathrm{t}}}$ | (13) |
| $\mu_{3}=\frac{\partial f_{1}\left(\Delta t, \delta_{\mathrm{t}}, t_{\mathrm{r}}, h_{\mathrm{h}}, \Delta t_{\mathrm{n}}\right)}{\partial t_{\mathrm{r}}}$ | (14) |
| $\mu_{4}=\frac{\partial f_{1}\left(\Delta t, \delta_{\mathrm{t}}, t_{\mathrm{r}}, h_{\mathrm{h}}, \Delta t_{\mathrm{n}}\right)}{\partial h_{\mathrm{h}}}$ | (15) |
| $\mu_{5}=\frac{\partial f_{1}\left(\Delta t, \delta_{\mathrm{t}}, t_{\mathrm{r}}, h_{\mathrm{h}}, \Delta t_{\mathrm{n}}\right)}{\partial \Delta t_{\mathrm{n}}}$ | (16) |
通过对凝汽器故障状态的分析, 针对凝汽器各故障状态下变化最大的参数, 选择循环冷却水压差Δp(循环水进出口压力之差)作为凝汽器健康度评价的辅助评价参数。
2 构建核电站凝汽器健康度评价模型
2.1 健康度评价参数集中单个因素的评分
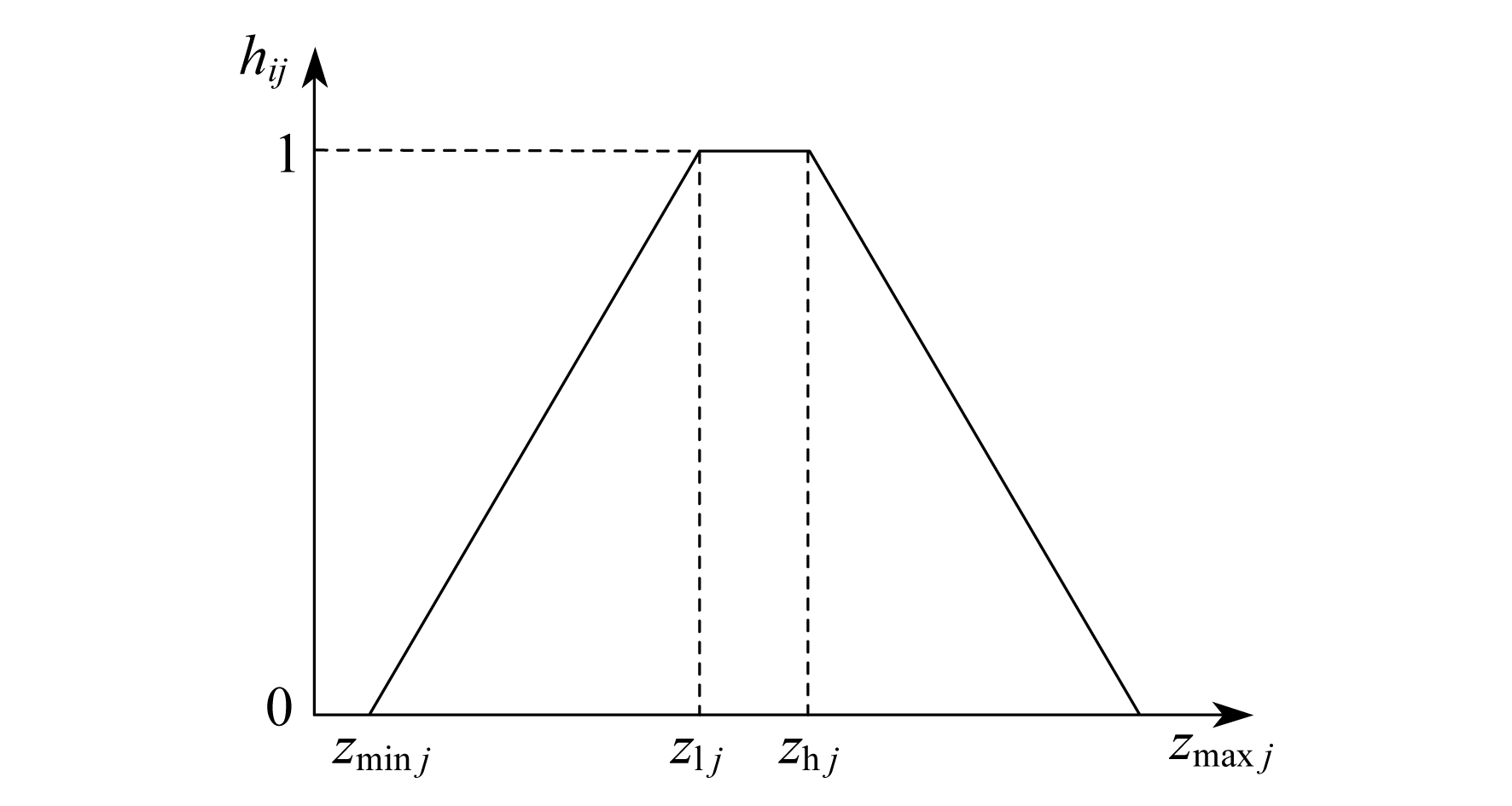
当核电机组处于稳定运行工况时, 凝汽器的各监视参数会在其对应的标准值上下一定的范围内波动。通过对设备的历史运行数据进行分析, 可以得到健康度评价参数集中第j个评价参数的标准值的上阈值zhj, 下阈值zlj, 最小极限值zmin j, 最大极限值zmax j。采用适当的方法对状态量进行定量描述的标准化处理。hij为第i种状态下对第j个评价参数的状态评分值, 状态评分值的取值范围为0~1, 当hij=0时表示此因素运行状态极差, 当hij=1时表示此因素运行状态极好。通过实际测量值zij偏离对应阈值的程度, 来度量因素运行状态的好坏。当实际的测量值偏离正常值的程度越小, 则对此因素的评价分值越高; 当实际的测量值偏离正常值的程度越大, 则对此因素的评价分值越低。实际测量值与其状态评分值的函数关系如图 1所示。
具体计算公式如下[9]
| $ h_{i j}=\left\{\begin{array}{cc} 0 & z_{i j} \lt z_{\min j} \\ \frac{z_{i j}-z_{\min j}}{z_{1 j}-z_{\min j}} & z_{i j} \in\left[z_{\min j}, z_{1 j}\right) \\ 1 & z_{i j} \in\left[z_{1 j}, z_{\mathrm{h} j}\right] \\ \frac{z_{\max j}-z_{i j}}{z_{\max j}-z_{\mathrm{h} j}} & z_{i j} \in\left(z_{\mathrm{h} j}, z_{\max j}\right] \\ 0 & z_{i j} \gt z_{\max j} \end{array}\right. $ | (17) |
通过对单个评价参数的运行状态评分, 能够提高健康度评价结果的客观性。综合凝汽器故障诊断中故障征兆阈值和限值的选取, 故障征兆参数值达到阈值, 认为征兆特征参数开始出现异常或者故障可能发生; 故障征兆参数值达到限值, 认为故障百分之百发生。核电机组处于稳定运行工况时, 凝汽器的各监视参数会在其对应的标准值上下一定的范围内波动。通过对设备的历史运行数据进行分析, 可以得到健康度评价参数的阈值和限值, 具体如表 1所示。
表 1
健康度评价模型中的阈值和限值
| 评价参数 | 上限值 zmax j |
上阈值 zhj |
下阈值 zlj |
下限值 zminj |
| 凝汽器压力Z1/kPa | 5.300 0 | 5.115 0 | — | — |
| 凝汽器液位Z2/m | 0.908 3 | 0.748 3 | — | — |
| 凝结水过冷却度Z3/℃ | 0.423 0 | 0.043 0 | — | — |
| 凝汽器端差Z4/℃ | 5.411 0 | 4.949 0 | — | — |
| 冷却水温升Z5/℃ | — | — | 8.30 | 8.10 |
| 冷却水压差Z6/kPa | 56.328 0 | 56.312 0 | 56.25 | 54.45 |
2.2 健康度评价参数权重系数的确定
对常权重系数的计算主要依赖系统运行异常与故障时刻的大量历史数据, 由此才能对系统的异常或故障状态进行客观准确的评价。对凝汽系统异常和故障状态进行分析, 不同的故障状态产生的过程中, 同一因素对应不同的故障会有不一样的变化程度, 且同一故障时刻, 不同的因素会有不同的变化程度, 而对应某些故障时, 有的因素可能是不变的。由于常权重的方法无法反应变化程度较大的因素对评判结果的影响程度, 因此本文引入基于变权重综合理论的变权原理。
2.2.1 评价参数常权重系数的确定
信息熵可以针对系统指标偏离正常值的程度进行度量。偏离程度越大, 信息熵越小, 该指标提供的信息量越大, 其权重也应越大; 反之, 信息熵越大, 其权重越小。因此, 可以利用信息熵计算出各指标的常权重系数, 为多指标综合评价提供比较客观的依据。
通过分析大量具有代表性的系统异常和故障时刻的数据, 形成原始评价参数数据矩阵
| $ \boldsymbol{Z}=\left(\begin{array}{cccccc} z_{11} & z_{12} & \cdots & z_{1 j} & \cdots & z_{1 n} \\ z_{21} & z_{22} & \cdots & z_{2 j} & \cdots & z_{2 n} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ z_{i 1} & z_{i 2} & \cdots & z_{i j} & \cdots & z_{i n} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ z_{m 1} & z_{m 2} & \cdots & z_{m j} & \cdots & z_{m n} \end{array}\right)_{m \times n} $ | (18) |
式中:zij——第i个异常或故障状态下第j个评价参数的实际数值, i=1, 2, 3, …, m; j=1, 2, 3, …, n。
在计算各评价参数的常权重系数时, 首先需要消除各评价参数状态量的量纲、数量级和因素类型的影响, 将各评价参数同度量化, 解决各项不同性质指标值的标准化问题。dj为第j个评价参数的正常值。当评价参数的变化趋势升高时, 即zij≥dj, 采用正向指标的计算公式对评价参数进行统一标准化; 当评价参数的变化趋势降低时, 即zij < dj, 采用负向指标的计算公式对评价参数进行统一标准化。其评价参数同度量化的具体方法如下[9]
| $ z_{i j}^{\prime}=\left\{\begin{array}{ll} \frac{z_{i j}-m i n\left(z_{j}\right)}{\max \left(z_{j}\right)-\min \left(z_{j}\right)} & z_{i j} \geqslant {d_j} \\ \frac{\max \left(z_{j}\right)-z_{i j}}{\max \left(z_{j}\right)-\min \left(z_{j}\right)} & z_{i j} \lt {d_j} \end{array}\right. $ | (19) |
第j个评价参数下第i个状态指标值的比重为
| $ p_{i j}=\frac{z_{i j}^{\prime}}{\sum\limits_{i=1}^{m} z_{i j}^{\prime}} $ | (20) |
第j个评价参数的熵值ej为
| $ e_{j}=-k \sum\limits_{i=1}^{m} p_{i j} \ln p_{i j} $ | (21) |
其中, k > 0且k=1/ln(n), ej > 0。
第j个评价参数的差异性系数为
| $g_{j}=1-e_{j}$ | (22) |
对差异性系数进行归一化, 第j个评价参数的常权重系数wj的计算公式为
| $ w_{j}=\frac{g_{j}}{\sum\limits_{j=1}^{n} g_{j}} $ | (23) |
其中, gj值越大表示指标越重要。
首先输入多组凝汽系统故障发生时刻的征兆参数历史数据, 结合熵值法计算凝汽系统健康度各评价参数的常权重系数, 结果如表 2所示。
表 2
凝汽器各评价参数的常权重系数
| 评价参数 | 常权重系数 | 评价参数 | 常权重系数 |
| $Z_{1}$ | 0.2401 | $Z_{4}$ | 0.2058 |
| $Z_{2}$ | 0.1543 | $Z_{5}$ | 0.0898 |
| $Z_{3}$ | 0.1762 | $Z_{6}$ | 0.1338 |
2.2.2 评价参数变权重系数的确定
变权法是指在综合评价中使得权重系数随各评价参数的评价值而改变的方法。文献[10]中给出的变权公式为
| $ w_{j}^{\prime}=\frac{w_{j}\left(y_{j}\right)^{-1}}{\sum\limits_{j=1}^{n} w_{j}\left(y_{j}\right)^{-1}} $ | (24) |
为了较为准确地反映设备状态各评价参数的权重大小, 引入均衡函数后的变权计算公式为
| $ W_{i j}=\frac{w_{j}\left(y_{i j}\right)^{\alpha-1}}{\sum\limits_{j=1}^{n} w_{j}\left(y_{i j}\right)^{\alpha-1}} $ | (25) |
式中:Wij——第i个状态下第j个评价参数的变权重系数, 0≤Wij≤1, ∑Wij=1;
yij——第i个状态下第j个评价参数所得评分值, 即对总体而言第j个评价参数的状态指标;
α——指数, 大小与各因素状态的均衡性有关, 根据对设备因素异常情况下变化程度的分析, 取α=0.5;
n——评价参数的个数。
因评价参数的评分值与状态量的劣化度对应, 评分值越高, 反映设备的状态越好, 所以可以用梯形隶属度函数推算得出其评分值。设yij的取值为0~1, 本文中yij为评价参数的评分值, 即yij=hij。
2.3 健康度评价参数模糊关系矩阵的建立
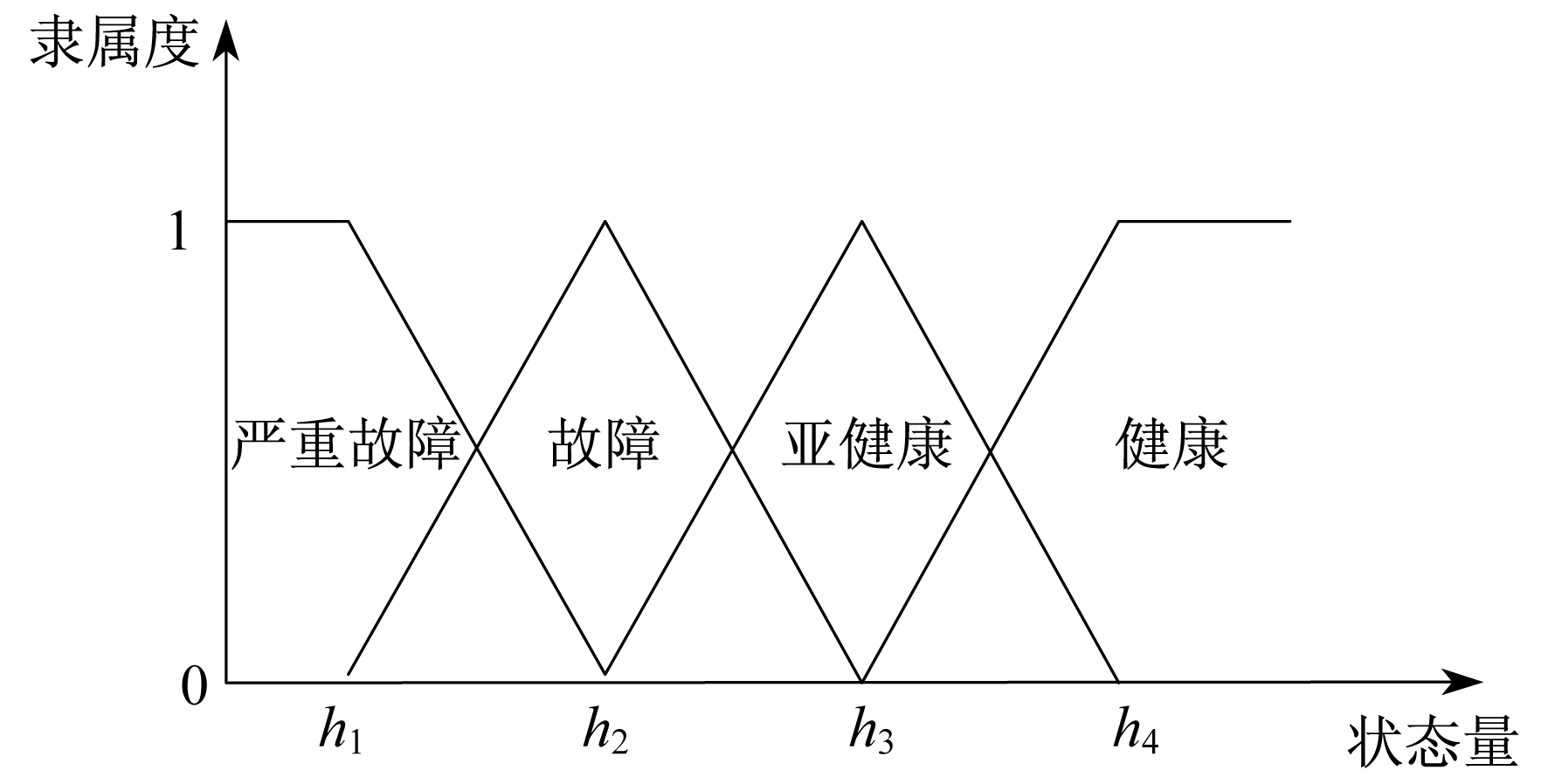
首先将各评价参数的实时值代入式(17), 计算得到各评价参数的状态评分值hij, 然后将单个评价参数的健康状况分为严重故障、故障、亚健康、健康4个等级。通过将评价参数的状态评分值代入隶属度函数计算公式, 算出单个评价参数评分值属于4个健康度等级的权重, 即可得到评价参数集的模糊关系矩阵。为了提高状态评价的合理性和准确性, 考虑到正态分布屏蔽掉了更多隶属度较低的信息, 三角梯形分布的两端分布隶属度无差异性不现实, 传统三角分布的两端分布没有梯形模糊集中心, 本文隶属度函数采用三角形分布和梯形分布相结合, 每个状态等级模糊集有中心, 即为隶属度分布中峰值最大点, 更准确地表达分布状态及隶属度。隶属分布如图 2所示。
隶属函数的表达式为
| $ r_{i 1}\left(h_{i j}\right)=\left\{\begin{array}{cc} 1 & h_{i j} \leqslant h_{1} \\ \frac{h_{2}-h_{i j}}{h_{2}-h_{1}} & h_{1} \lt h_{i j} \leqslant h_{2} \\ 0 & h_{2} \lt h_{i j} \end{array}\right. $ | (26) |
| $ r_{i 2}\left(h_{i j}\right)=\left\{\begin{array}{cc} \frac{h_{i j}-h_{1}}{h_{2}-h_{1}} & h_{1} \lt h_{i j} \leqslant h_{2} \\ \frac{h_{3}-h_{i j}}{h_{3}-h_{2}} & h_{2} \lt h_{i j} \leqslant h_{3} \\ 0 & h_{i j} \leqslant h_{1}, h_{3} \lt h_{i j} \end{array}\right. $ | (27) |
| $ r_{i 3}\left(h_{i j}\right)=\left\{\begin{array}{cc} \frac{h_{i j}-h_{2}}{h_{3}-h_{2}} & h_{2} \lt h_{i j} \leqslant h_{3} \\ \frac{h_{4}-h_{i j}}{h_{4}-h_{3}} & h_{3} \lt h_{i j} \leqslant h_{4} \\ 0 & h_{i j} \leqslant h_{2}, h_{4} \lt h_{i j} \end{array}\right. $ | (28) |
| $ r_{i 4}\left(h_{i j}\right)=\left\{\begin{array}{cc} 0 & h_{i j} \leqslant h_{3} \\ \frac{h_{i j}-h_{3}}{h_{4}-h_{3}} & h_{3} \lt h_{i j} \leqslant h_{4} \\ 1 & h_{4} \lt h_{i j} \end{array}\right. $ | (29) |
式中:rik(hij)——状态量对严重故障(k=1)、故障(k=2)、亚健康(k=3)、健康(k=4)4个状态级别的隶属度函数;
h1, h2, h3, h4——状态量的状态级别对应的模糊分界区间界线, 本文取h1=0.1, h2=0.3, h3=0.6, h4=0.9。
根据单个评价参数对于严重故障、故障、亚健康、健康4个状态级别的隶属度函数构成的模糊关系矩阵, 可得单因素评价矩阵为
| $ \boldsymbol{R}_{i}=\left[\begin{array}{cccc} r_{i 11} & r_{i 12} & r_{i 13} & r_{i 14} \\ r_{i 21} & r_{i 22} & r_{i 23} & r_{i 24} \\ \vdots & \vdots & \vdots & \vdots \\ r_{i m 1} & r_{i m 2} & r_{i m 3} & r_{i m 4} \end{array}\right] $ | (30) |
式中:Ri——i时刻对应的单因素评价矩阵;
rijk——i时刻第j个评价参数对于第k个健康状态级别的隶属度, 其中j=1, 2, 3, …, m, 且k=1, 2, 3, 4分别表示表示第k个评价参数对于严重故障、故障、亚健康、健康4个状态级别的权重;
m——健康度评价参数集中因素的个数。
2.4 健康度评价模型中评语集的构建
采用综合加权法对设备多特征参数健康状态进行评价, 通过变权理论得到各因素的变权重系数矩阵与单因素评价矩阵, 将两者相乘得到系统健康状态的模糊关系矩阵。其表达式如下[11]
| $\boldsymbol{S}_{i}=\left[\begin{array}{llll}s_{i 1} & s_{i 2} & s_{i 3} & s_{i 4}\end{array}\right]=\left[\begin{array}{llll}W_{i 1} & W_{i 2} & \cdots & W_{i m}\end{array}\right] \cdot \\ \left[\begin{array}{cccc}r_{i 11} & r_{i 12} & r_{i 13} & r_{i 14} \\ r_{i 21} & r_{i 22} & r_{i 23} & r_{i 24} \\ \vdots & \vdots & \vdots & \vdots \\ r_{i m 1} & r_{i m 2} & r_{i m 3} & r_{i m 4}\end{array}\right]$ | (31) |
式中:si1, si2, si3, si4——第i个状态下系统健康状态对于严重故障、故障、亚健康、健康4个状态级别的权重, 取值范围为0~1。
隶属度函数完成了从精确的测量值到健康状态等级的权重这一模糊量的模糊化过程, 而由隶属度计算健康度的公式则实现了从健康状态等级的权重这一模糊量到健康度精确量的去模糊化过程。通过对系统的具体情况进行分析, 确定由隶属度计算健康度的公式如下
| $ \begin{array}{l} H_{i}=f\left(\boldsymbol{S}_{i}\right)=f\left(s_{i 1}, s_{i 2}, s_{i 3}, s_{i 4}\right)= \\ \frac{k_{1} s_{i 1}+k_{2} s_{i 2}+k_{3} s_{i 3}+k_{4} s_{i 4}-k_{1}}{k_{1}-k_{4}} \end{array} $ | (32) |
式中:k1, k2, k3, k4——待定系数, 由系统的具体情况确定, k1≤k2≤k3≤k4。
k1, k2, k3, k4也可以理解为不同状态等级的分值, 系统劣化状态越严重, 得分越低。将系统总和的健康状态得分归一化得到系统的综合健康度, 其等级划分如表 3所示。
表 3
综合健康度等级划分
| 健康状况等级 | 健康度取值范围 | 健康状况描述 |
| 健康 | $0.9 < H_{i} \leqslant 1$ | 设备运行状态非常好 |
| 亚健康 | $0.5 < H_{i} \leqslant 0.9$ | 评价参数集出现异常参数, 设备不应长期连续运行 |
| 故障 | $0.2 < H_{i} \leqslant 0.5$ | 出现故障, 应在较短时间内对设备停机进行检修 |
| 严重故障 | $0 \leqslant H_{i} \leqslant 0.2$ | 设备不能运行, 应立即停机进行检修 |
3 凝汽器健康度计算实例
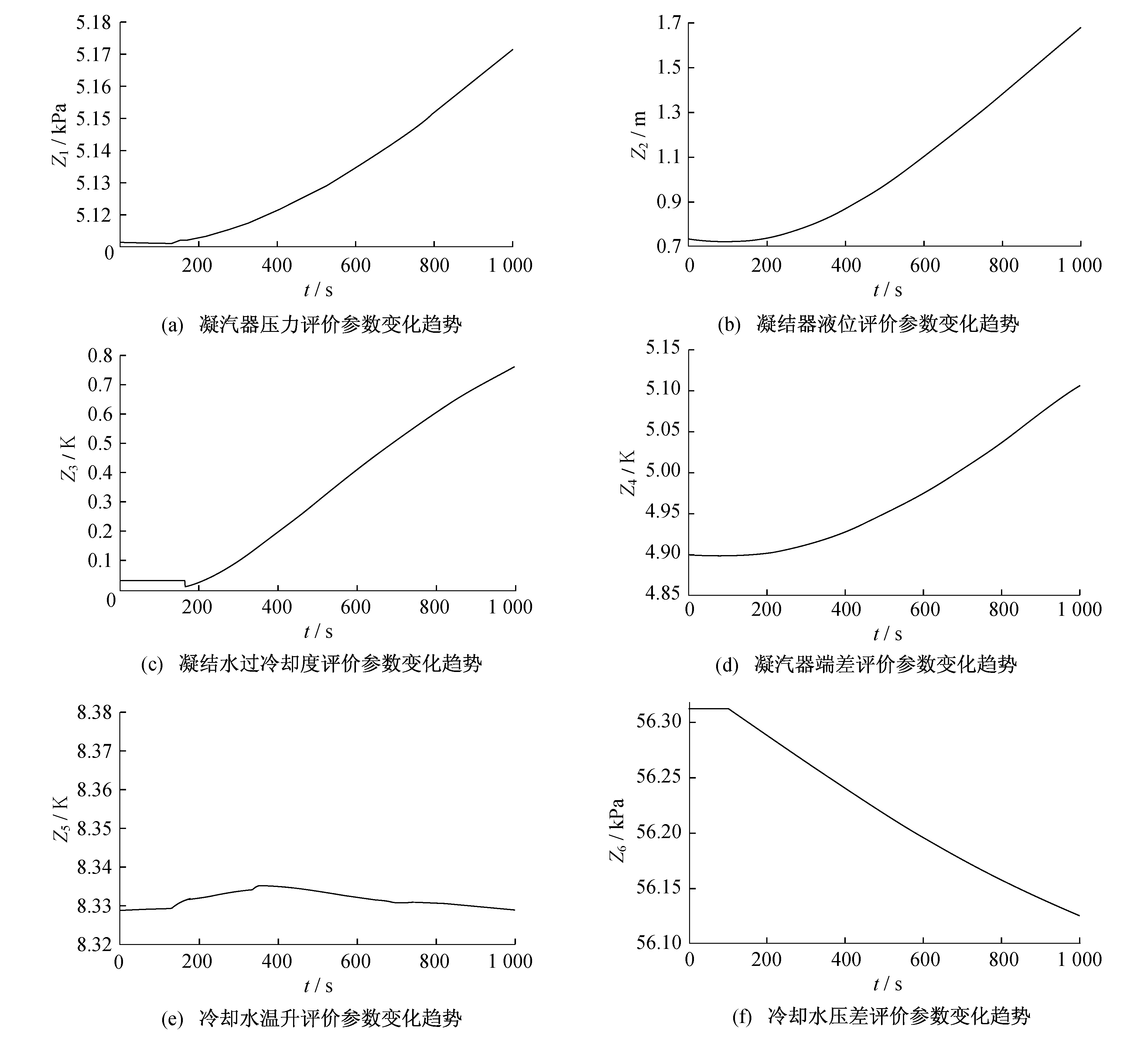
在实际运行中, 核电站凝汽器受高温高压的流体冲刷、侵蚀和振动等因素影响, 导致其泄漏故障的可能性很大, 因此选用凝汽器冷却水铜管泄漏故障的渐变过程来验证健康度评价模型的正确性。基于核电站凝汽器故障机理模型建立其仿真系统, 当核电仿真系统运行在100% FP(满负荷)工况时, 在核电站仿真系统的故障设置窗口引入凝汽器冷却水铜管泄漏故障, 且设置泄漏程度为0.3%, 取前1 000 s的数据即可反应从正常状态到故障状态的变化过程。凝汽器冷却水铜管泄漏故障渐变过程各评价参数的变化趋势如图 3所示。
由图 3可知, 除了冷却水温升在正常范围内波动外, 其他因素的变化程度都比较大。由故障反应过程可知, 冷却水温升存在延时性。根据每个评价参数的阈值限值和图 3对应各数据的输入数据, 利用式(11)可计算出不同时刻各评价参数的状态评分值。
通过式(11)、式(24)、式(25)对图 3中各评价参数实时值进行计算, 得到各评价参数不同时刻的变权重系数。由于健康度评价模型中同一时刻所有评价参数的变权重之和为1, 因此对应不同时刻的某评价参数的变权重会随着该评价参数相对其本身阈值限值的变化程度和其他评价参数相对其本身阈值限值的变化程度而变化。该方法更加客观地体现了实时值相对正常值的变化情况。各评价参数不同时刻的变权重系数如表 4所示, 其中表 4中的运行时间与图 3中的时间对应。
表 4
各评价参数不同时刻的变权重系数
| 运行时间/s | 变权重系数 | |||||
| Z1 | Z2 | Z3 | Z4 | Z5 | Z6 | |
| 1 | 0.240 1 | 0.154 3 | 0.176 2 | 0.205 8 | 0.089 8 | 0.133 8 |
| 100 | 0.240 0 | 0.154 6 | 0.176 1 | 0.205 7 | 0.089 8 | 0.133 8 |
| 200 | 0.238 6 | 0.155 5 | 0.175 1 | 0.204 5 | 0.089 2 | 0.137 1 |
| 300 | 0.234 5 | 0.157 0 | 0.183 2 | 0.197 4 | 0.086 1 | 0.141 7 |
| 400 | 0.235 4 | 0.158 2 | 0.202 7 | 0.182 4 | 0.079 6 | 0.141 6 |
| 500 | 0.234 0 | 0.159 8 | 0.244 1 | 0.159 8 | 0.069 7 | 0.135 6 |
| 600 | 0.177 0 | 0.130 0 | 0.446 9 | 0.105 4 | 0.044 7 | 0.096 0 |
| 700 | 0.222 6 | 0.202 4 | 0.344 9 | 0.095 9 | 0.039 3 | 0.094 8 |
| 800 | 0.344 2 | 0.221 2 | 0.252 6 | 0.073 3 | 0.028 8 | 0.079 8 |
| 900 | 0.337 8 | 0.217 0 | 0.247 9 | 0.075 6 | 0.028 2 | 0.093 4 |
| 1 000 | 0.328 3 | 0.211 0 | 0.240 9 | 0.077 5 | 0.027 5 | 0.114 8 |
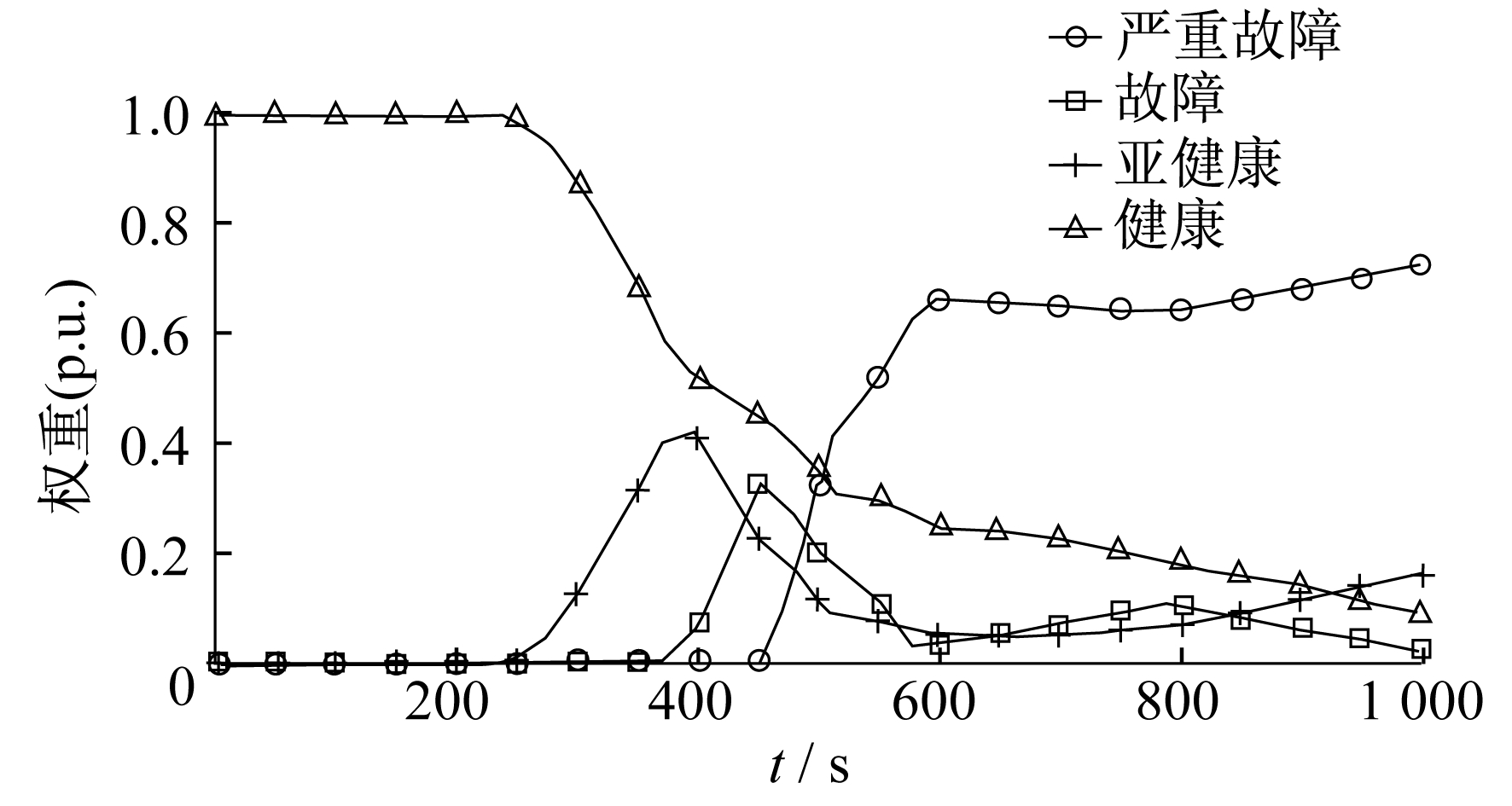
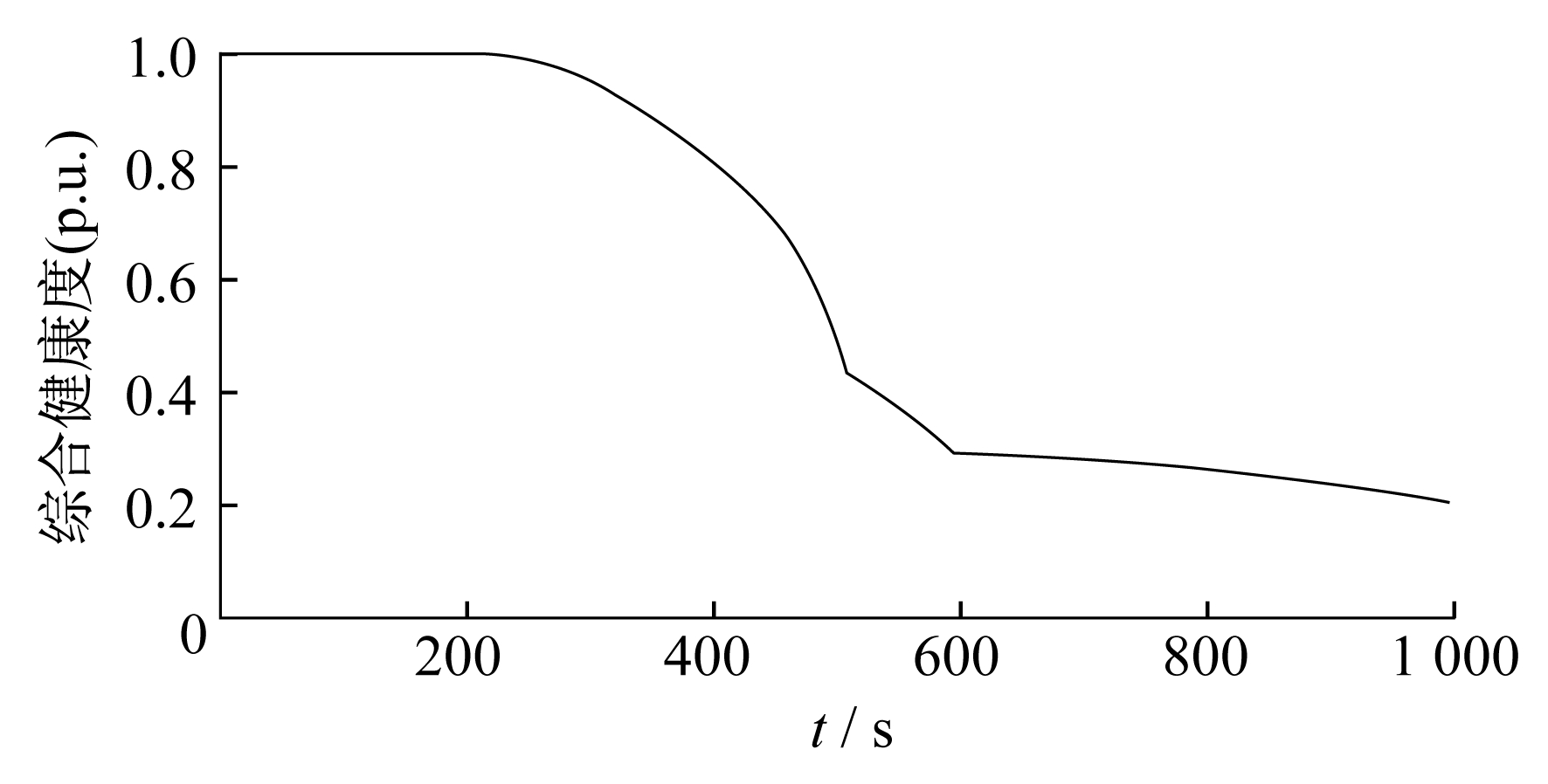
根据本文提出的方法得到凝汽器冷却水铜管泄漏故障发生过程中评价参数健康状态的权重曲线如图 4所示。利用式(32)计算得到系统综合健康度, 结果如图 5所示。
图 5的健康度曲线能够很好地反映凝汽器综合健康状态的变化, 为维修运行人员提供参考。当健康度进入异常状态时, 该方法能够实现故障的早期预报, 避免发生严重故障, 提高了核电站凝汽系统运行的安全性和可靠性。
4 结语
本文通过对以凝汽器机理故障模型为基础的数据来源进行分析, 得到设备健康状态评价参数集; 以评价参数作为失效依据, 先计算各评价参数的健康指数; 然后利用引入均衡函数后的变权公式计算权重, 运用综合加权法建立设备多参数健康度评价模型。凝汽器健康度评价模型对凝汽器健康度计算实例结果表明, 该方法通过对凝汽器评价参数的计算, 综合得到一个健康度的值, 将凝汽器的运行状态是否正常准确化, 能够准确反映凝汽器的运行状态。
参考文献
-
[1]基于模糊数据融合的健康评价方法[J]. 测试技术学报, 2006, 20(3): 264-269. DOI:10.3969/j.issn.1671-7449.2006.03.014
-
[2]基于DSmT和模糊综合评判的健康状态评估方法[J]. 计算机测量与控制, 2015, 23(11): 3697-3700.
-
[3]基于层次分析结构的变压器健康状态与综合寿命评估模型[J]. 电网技术, 2014, 38(10): 2845-2850.
-
[4]彭颖.基于退化隐式半马尔科夫模型的设备健康预测及系统性维护策略研究[D].上海: 上海交通大学, 2011.
-
[5]风力发电机组的健康评估[J]. 新能源进展, 2014(6): 430-433. DOI:10.3969/j.issn.2095-560X.2014.06.004
-
[6]复杂装备健康状态评估的粗糙核距离度量方法[J]. 计算机工程与设计, 2009, 30(18): 4269-4271.
-
[7]航空发动机健康评估变精度粗糙集决策方法[J]. 航空动力学报, 2013, 28(2): 283-289.
-
[8]600 MW机组凝汽器性能分析与循环水系统优化研究[J]. 电站系统工程, 2012(6): 59-62.
-
[9]基于健康指数的设备运行状态评价与预测[J]. 合肥工业大学学报(自然科学版), 2015(10): 1318-1323.
-
[10]基于变权综合理论和模糊综合评价的多结果输出输电线路运行状态评价方法[J]. 高电压技术, 2017, 43(4): 1289-1295.
-
[11]ZHENG H L, WANG R X, XU M Q. Study on the variable weight method for gearbox fuzzy state evaluation[J]. Applied Mechanics & Materials, 2014, 32(8): 651-653.