|
|
|
发布时间: 2019-10-10 |
|
|
|
|
收稿日期: 2019-04-02
基金项目: 国家自然科学基金(61573239);上海市重点科技攻关计划(14110500700);上海市电站自动化技术重点实验室项目(13DZ2273800)
中图法分类号: TM464
文献标识码: A
文章编号: 1006-4729(2019)05-0435-07
|
摘要
针对传统的双PI控制存在电流谐波高、系统稳定性差以及响应速度慢的不足, 提出了一种基于Lyapunov函数的T型并网逆变器的控制策略。在分析T型逆变器数学模型的基础上, 设计了电压-电流双闭环控制回路。从稳定性角度出发, 针对电流内环提出了基于Lyapunov函数的非线性控制策略, 以实现谐波参考电流的快速跟踪; 外环采用传统的PI控制, 以实现对直流侧电容电压的跟踪; 同时, 将电压外环输出的d轴期望电流作为电流内环的变量输入, 以提高双环的抗扰动性。最后, 将提出的新型双环控制策略与传统的双PI控制策略进行了仿真比较, 验证了所提策略在补偿谐波方面的优越性。
关键词
Lyapunov函数; T型逆变器; 电压-电流双闭环; 电流谐波; 稳定性
Abstract
In view of the disadvantages of high current harmonics, poor system stability and slow response speed in the traditional double PI control, this paper presents a control strategy for T-type grid-connected inverter based on the Lyapunov function.On the basis of analyzing the mathematical model of T-type inverter, a voltage-current double closed loop control circuit is designed.From the point of view of stability, a nonlinear control strategy based on Lyapunov function is proposed for the inner loop of current, which realizes the fast tracking of harmonic reference current.The outer loop adopts the traditional PI control to track the capacitor voltage of DC side.Meanwhile, the d-axis expected current from the outer loop is used as the variable input of the inner loop, which improves the anti-disturbance performance of the double loop.Finally, compare the new double loop control strategy proposed with the traditional double PI control strategy in simulation, and the comparison results verify the superiority of the new double loop control strategy in harmonic compensation.
Key words
Lyapunov function; T-type inverter; voltage-current double closed loop; current harmonic; stability
随着能源危机与环境污染的日趋严重, 利用太阳能、风能等分布式能源的发电技术一直是国内外学者的研究热点[1]。并网逆变器作为光伏发电系统与电网之间的接口设备, 其控制性能直接影响整个并网系统的可靠性与稳定性[2]。传统的两电平逆变器存在谐波电流高、电压等级低等不足, T型三电平逆变器的提出, 解决了上述存在的问题。与传统的NPC型三电平相比, T型逆变器具有导通损耗小、效率高等优点[3]。
目前, 并网逆变器的控制策略普遍采用传统比例积分(PI)控制、比例谐振(PR)控制、预测控制等。其中, 传统PI控制受比例参数和积分参数影响较大, 故控制系统的稳定性差且控制输出电流谐波高[4]。PR控制可以对特定频率的正弦信号实现无静差跟踪, 但是对非线性负载的高次谐波抑制较差[5-6]。当系统受到外在变量的瞬时扰动时, 无差拍控制对其具有较好的抑制效果, 但系统受到周期性扰动之时, 这种控制的抑制效果并不理想[7]。文献[8]提出了一种电流内环采用重复PR控制的新型电流双环控制策略, 可以有效抑制电网电压波动和非线性负载对并网电流的影响, 但闭环传递函数的求解比较复杂, 且阻尼参数的选取不够精确。文献[9]指出, 滑模变结构具有良好的自适应性、较强的鲁棒性、良好的动态和稳态性能, 但是滑模变结构中滑模控制规律设计的参数较多, 难以选择。为了更好地实现逆变器的非线性控制, 文献[10]将Lyapunov函数应用到逆变器系统的并网控制之中, 能够提高系统的稳定性, 降低输出电流谐波。文献[11-12]将Lyapunov函数控制方法与传统的PI控制策略相比, 该方法具有更好的稳态谐波电流跟踪精度。文献[13]将Lyapunov函数控制与PR控制相结合, 在保证系统全局稳定性的同时, 能够对电网电流进行无静差追踪, 并可确定逆变器的参考电流值。
本文将Lyapunov函数应用于T型三电平并网逆变器的控制中。首先, 介绍了T型三电平逆变器的数学模型; 其次, 根据逆变器的数学模型推导具有开关函数的数学表达式, 并依据Lyapunov函数的能量函数表达式进行电流内环的设计, 其中的电压外环采用传统的PI控制, 以实现直流侧电容电压的跟踪, 且电压外环的输出作为电流内环的输入; 最后, 通过仿真实验, 验证了本文所提策略的优越性。
1 T型三电平逆变器的结构
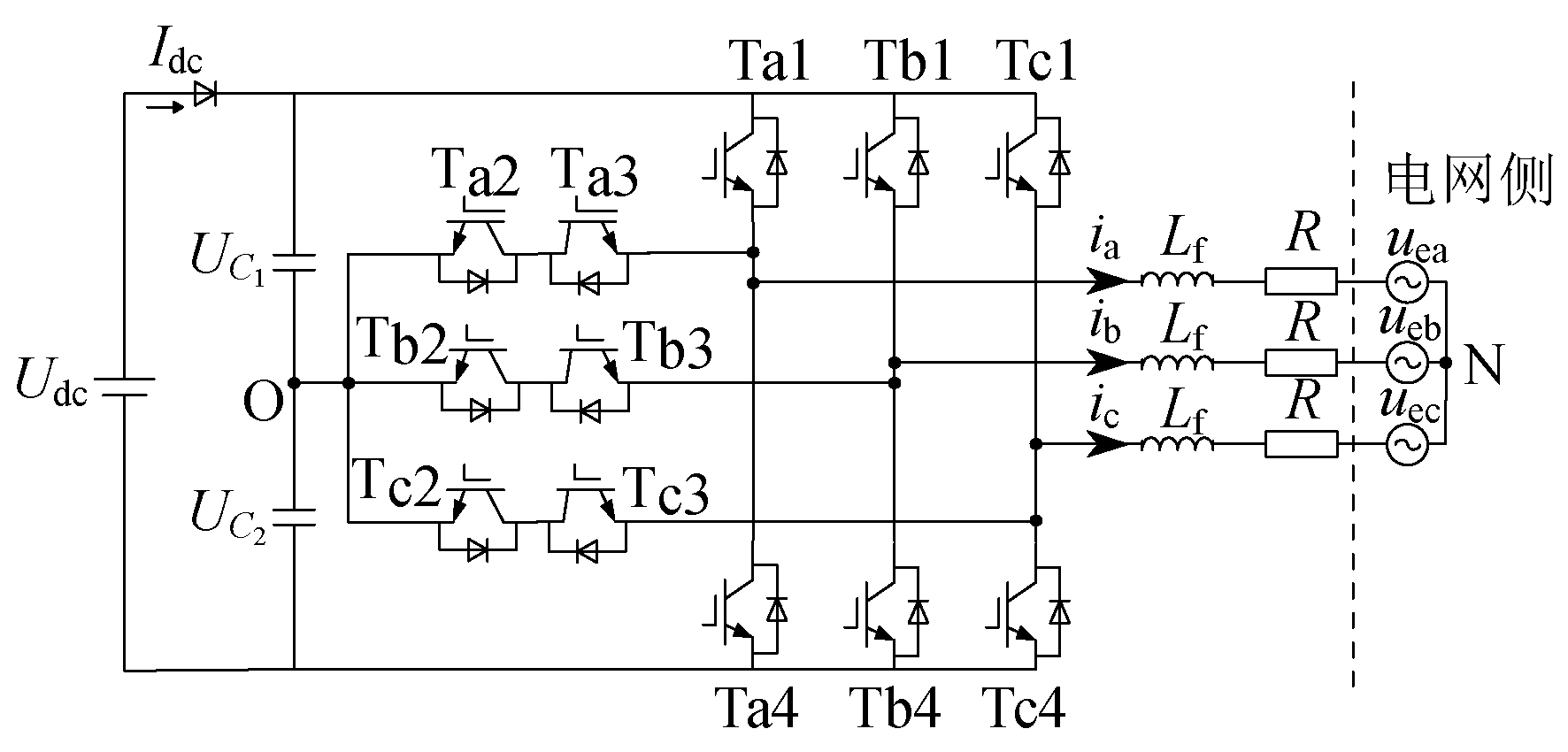
1.1 T型三电平逆变器的拓扑结构
1.2 T型三电平逆变器的数学模型
文献[5]已经给出了T型三电平逆变器的数学模型, 这里不再赘述。经abc-dq坐标变换之后, 在dq旋转坐标下T型三电平逆变器的数学模型为
| $ \left\{\begin{array}{l} L \frac{\mathrm{d} i_{d}}{\mathrm{d} t}=\omega Li_{q}-Ri_{d}+\left(S_{d1} U_{C_{1}}-S_{d 4} U_{C_{2}}\right)-u_{\mathrm{e} d} \\ L \frac{\mathrm{d} i_{q}}{\mathrm{d} t}=-\omega Li_{d}+Ri_{q}+\left(S_{q1} U_{C_{1}}-S_{q 4} U_{C_{2}}\right)-u_{\mathrm{e} q} \\ C \frac{\mathrm{d} U_{C_{1}}}{\mathrm{d} t}=-S_{d1} i_{d}-S_{{q1}} i_{q}+I_{\mathrm{dc} } \\ C \frac{\mathrm{d} U_{C_{2}}}{\mathrm{d} t}=S_{d 4} i_{d}+S_{q 4} i_{q}+I_{\mathrm{dc}} \end{array}\right. $ | (1) |
式中:L——三相线路的等效电感, L=Lf;
id, iq——三相电流ia, ib, ic在d轴和q轴上的分量;
UC1, UC2——分压电容C1和C2的电压;
ued, ueq——网侧三相电压uea, ueb, uec在d轴和q轴上的分量;
Sd1, Sq1——A相上桥臂开关函数Sa1在d轴和q轴上的分量;
Sd4, Sq4——A相下桥臂开关函数Sa4在d轴和q轴上的分量。
2 T型三电平逆变器空间矢量脉宽调制算法
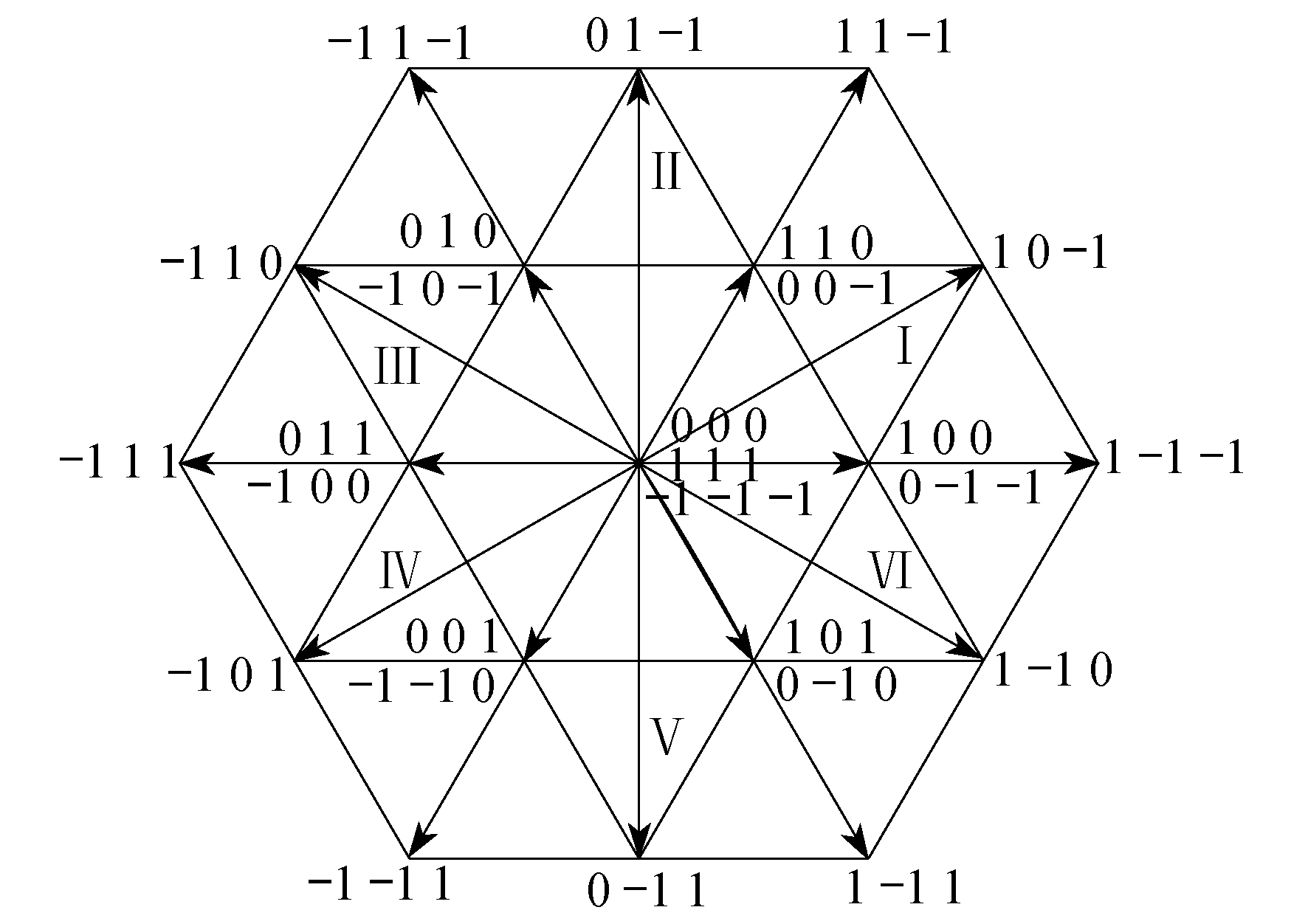
对于T型三电平逆变器, 将每相桥臂的3种开关状态分别记为1, 0, -1。以A相为例:1代表开关管Ta1和Ta2同时导通; 0代表两个开关管Ta2和Ta3同时导通; -1代表两个开关管Ta3和Ta4同时导通。B相和C相同例。每相桥臂有3种开关状态, 三相桥臂共有33=27种开关状态。T型三电平逆变器的基本空间电压矢量图如图 2所示。
由图 2可以看出, 27个空间电压矢量可以分为大矢量、中矢量、小矢量和零矢量4类, 具体分类如表 1所示。
表 1
空间电压矢量分类
| 矢量分类 | 所有矢量 |
| 大 | 1-1-1, 11-1, -11-1, -111, -1-11, 1-11 |
| 中 | 10-1, 01-1, -110, -101, 0-11, 1-10 |
| 小 | 100(0-1-1), 110(00-1), 010(-10-1) 011(-100), 001(-1-10), 101(0-10) |
| 令 | 000, 111, -1-1-1 |
简单来说, T型三电平逆变器的空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)算法主要可以分为4个部分, 分别为:空间矢量区域判断; 矢量状态次序确定; 矢量作用时间计算; 时间状态分配。
3 电流内环控制器设计
令状态变量x=[id, iq, UC1, UC2]T, 输入变量u=[Sd1, Sd4, Sq1, Sq4]T, 期望状态变量:
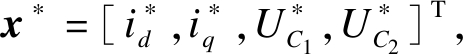 则暂态条件下系统在dq坐标系下的状态方程为
则暂态条件下系统在dq坐标系下的状态方程为
| $\left\{\begin{array}{l}L \frac{\mathrm{d} i_{d}^{*}}{\mathrm{d} t}=\omega L i_{q}^{*}-R i_{d}^{*}+\left(\bar{S}_{d 1} U_{C_{1}}^{*}-\bar{S}_{d 4} U_{C_{2}}^{*}\right)-u_{\mathrm{e}d} \\ L \frac{\mathrm{d} i_{q}^{*}}{\mathrm{d} t}=-\omega L i_{d}^{*}-R i_{q}^{*}+\left(\bar{S}_{q 1} U_{C_{1}}^{*}-\bar{S}_{q4} U_{C_{2}}^{*}\right)-u_{\mathrm{e}q} \\ C \frac{\mathrm{d} U_{C_{1}}^{*}}{\mathrm{d} t}=-\bar{S}_{d 1} i_{d}^{*}-\bar{S}_{q 1} i_{q}^{*}+I_{\mathrm{dc}} \\ C \frac{\mathrm{d} U_{C_{2}}^{*}}{\mathrm{d} t}=\bar{S}_{d 4} i_{d}^{*}+\bar{S}_{q 4} i_{q}^{*}+I_{\mathrm{dc}}\end{array}\right.$ | (2) |
式中:
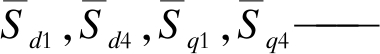 暂态时dq坐标系下的开关函数。
暂态时dq坐标系下的开关函数。
本文采用SVPWM调制策略。为保持开关函数的对称性, 暂态开关函数选择为[13]
| $ \left\{\begin{array}{l} \bar{S}_{d 1}=\frac{\bar{S}_{d 1}-\bar{S}_{d 4}}{2}, \quad \bar{S}_{d 1}=-\bar{S}_{d 4} \\ \bar{S}_{q 1}=\frac{\bar{S}_{q 1}-\bar{S}_{q 4}}{2}, \quad \bar{S}_{q 1}=-\bar{S}_{q 4} \end{array}\right. $ | (3) |
令UC1=UC2=UC, 则式(2)可以化简为
| $ \left\{\begin{array}{l} L \frac{\mathrm{d} i_{d}^{*}}{\mathrm{d} t}=\omega L i_{q}^{*}-R i_{d}^{*}+2 \bar{S}_{d 1} U_{C_{1}}-u_{\mathrm{e} d} \\ L \frac{\mathrm{d} i_{q}^{*}}{\mathrm{d} t}=-\omega L i_{d}^{*}-R i_{q}^{*}+2 \bar{S}_{q 1} U_{C}-u_{\mathrm{e} q} \end{array}\right. $ | (4) |
结合式(3)可得暂态时dq坐标系下开关函数的关系式为
| $ \left\{\begin{array}{l} \bar{S}_{d 1}=\frac{u_{\mathrm{e} d}+R i_{d}^{*}-\omega L i_{q}^{*}+L \frac{\mathrm{d} i_{d}^{*}}{\mathrm{d} t}}{2 U_{C}} \\ \bar{S}_{q 1}=\frac{u_{\mathrm{e}q}+R i_{q}^{*}-\omega L i_{d}^{*}+L \frac{\mathrm{d} i_{q}^{*}}{\mathrm{d} t}}{2 U_{C}} \end{array}\right. $ | (5) |
令输出变量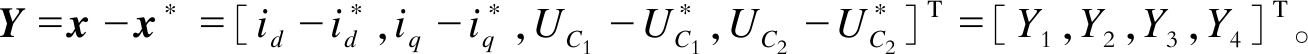
化简式(1)和式(2), 可以得到:
| $\left\{\begin{array}{l}\frac{\mathrm{d} i_{d}}{\mathrm{d} t}=\frac{\omega L i_{q}-R i_{d}+\left(S_{d 1} U_{C_{1}}-S_{d 4} U_{C_{2}}\right)-u_{\mathrm{e} d}}{L} \\ \frac{\mathrm{d} i_{q}}{\mathrm{d} t}=\frac{-\omega L i_{d}+R i_{q}+\left(S_{q 1} U_{C_{1}}-S_{q 4} U_{C_{2}}\right)-u_{\mathrm{e}q}}{L} \\ \frac{\mathrm{d} U_{C_{1}}}{\mathrm{d} t}=\frac{-S_{d 1} i_{d}-S_{q 1} i_{q}+I_{\mathrm{dc}}}{C} \\ \frac{\mathrm{d} U_{C_{2}}}{\mathrm{d} t}=\frac{S_{d 4} i_{d}+S_{q 4} i_{q}+I_{\mathrm{dc}}}{C}\end{array}\right.$ | (6) |
| $\left\{\begin{array}{l}\frac{\mathrm{d} i_{d}^{*}}{\mathrm{d} t}=\frac{\omega L i_{q}^{*}-R i_{d}^{*}+\left(\bar{S}_{d 1} U_{C_{1}}^{*}-\bar{S}_{d 4} U_{C_{2}}^{*}\right)-u_{\mathrm{e} d}}{L} \\ \frac{\mathrm{d} i_{q}^{*}}{\mathrm{d} t}=\frac{-\omega L i_{d}^{*}-R i_{q}^{*}+\left(\bar{S}_{q 1} U_{C_{1}}^{*}-\bar{S}_{q 4} U_{C_{2}}^{*}\right)-u_{\mathrm{e}q}}{L} \\ \frac{\mathrm{d} U_{C_{1}}^{*}}{\mathrm{d} t}=\frac{-\bar{S}_{d 1} i_{d}^{*}-\bar{S}_{q 1} i_{q}^{*}+I_{\mathrm{dc}}}{C} \\ \frac{\mathrm{d} U_{C_{2}}^{*}}{\mathrm{d} t}=\frac{\bar{S}_{d 4} i_{d}^{*}+\bar{S}_{q 4} i_{q}^{*}+I_{\mathrm{dc}}}{C}\end{array}\right.$ | (7) |
式(6)减去式(7), 可以得到
| $ \left\{ \begin{array}{l} {\begin{aligned} \dot{Y}_{1}=& \frac{\omega L\left(i_{q}-i_{q}^{*}\right)-R\left(i_{d}-i_{d}^{*}\right)}{L}+\\ & \frac{\left(S_{d 1} U_{C_{1}}-\bar{S}_{d 1} U_{C_{1}}^{*}\right)-\left(S_{d 4} U_{C_{2}}-\bar{S}_{d 4} U_{C_{2}}^{*}\right)}{L} \\ \dot{Y}_{2}=& \frac{-\omega L\left(i_{d}-i_{d}^{*}\right)+R\left(i_{q}-i_{q}^{*}\right)}{L}+\\ & \frac{\left(S_{q 1} U_{C_{1}}-\bar{S}_{q 1} U_{C_{1}}^{*}\right)-\left(S_{q 4} U_{C_{2}}-\bar{S}_{q 4} U_{C_{2}}^{*}\right)}{L} \end{aligned}} \\ {\dot{Y}_{3}=\frac{-\left(S_{d 1} i_{d}-\bar{S}_{d 1} i_{d}^{*}\right)-\left(S_{q 1} i_{q}-\bar{S}_{q 1} i_{q}^{*}\right)}{C} \\ \dot{Y}_{4}=\frac{\left(S_{d 4} i_{d}-\bar{S}_{d 4} i_{d}^{*}\right)+\left(S_{q 4} i_{q}-\bar{S}_{q 4} i_{q}^{*}\right)}{C}}\\ \end{array} \right. $ | (8) |
令Lyapunov函数的能量函数H(Y)为
| $ H(\boldsymbol{Y})=\frac{L}{2}\left(Y_{1}^{2}+Y_{2}^{2}\right)+\frac{C}{2}\left(Y_{3}^{2}+Y_{4}^{2}\right) $ | (9) |
对式(9)两边求导, 可以得到
| $\dot{H}(\boldsymbol{Y})=L\left(Y_{1} \dot{Y}_{1}+Y_{2} \dot{Y}_{2}\right)+ \\ C\left(Y_{3} \dot{Y}_{3}+Y_{4} \dot{Y}_{4}\right)$ | (10) |
结合式(8)与式(10), 可以得到
| $\left(\begin{array}{l}S_{d 1}=\bar{S}_{d 1}+\alpha_{1}\left(Y_{1} U_{C_{1}}^{*}-Y_{3} i_{d}^{*}\right) \\ S_{d 4}=\bar{S}_{d 4}+\alpha_{1}\left(Y_{4} i_{d}^{*}-Y_{1} U_{C_{2}}^{*}\right) \\ S_{q 1}=\bar{S}_{q 1}+\beta_{1}\left(Y_{2} U_{C_{1}}^{*}-Y_{3} i_{q}^{*}\right) \\ S_{q 4}=\bar{S}_{q 4}+\beta_{1}\left(Y_{4} i_{q}^{*}-Y_{2} U_{C_{2}}^{*}\right)\end{array}\right.$ | (11) |
式中:α1, β1——d轴和q轴的控制增益, 其值均小于零。
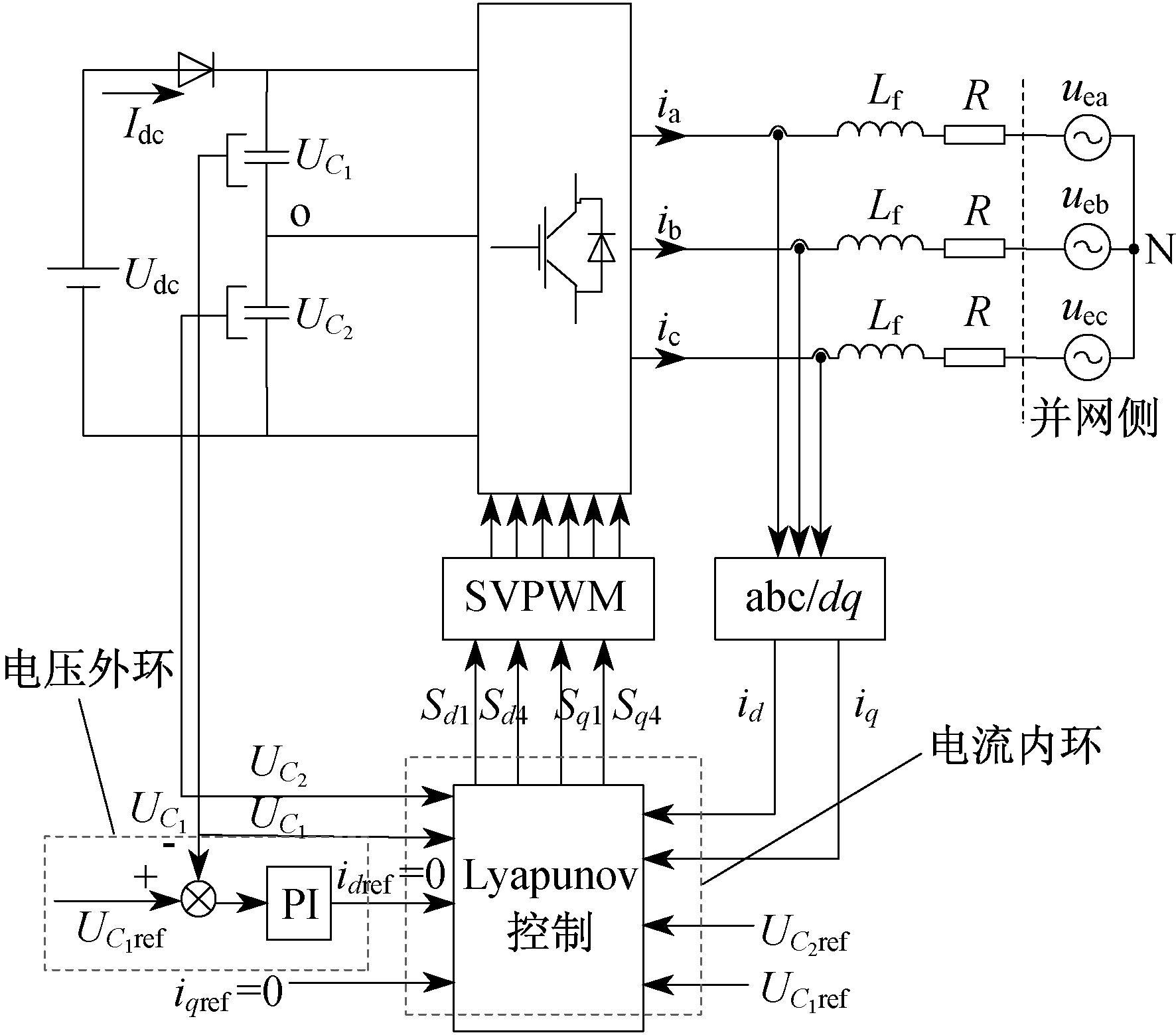
为了保证dq轴控制上的对称性, 令α1=β1。至于系统控制增益的选择, 文献[13]已经详细介绍, 这里不再赘述。综上所述, 基于Lyapunov函数的T型三电平并网逆变器双环控制框图如图 3所示。
图 3中, 本文采用电压-电流双环控制系统。其中:电压外环采用传统的PI控制, 且控制器的输入为直流侧上电容电压的实际值与理想值的差值, 其目的是跟踪直流侧电容电压, 抑制中性点电容电压偏移; 电流内环采用基于Lyapunov函数的控制方法, 内环控制器的输入为UC1, UC2, UC1ref, UC2ref, id, iq, idref, iqref。为了保证单位功率因数输出, 令iqref=0, 直轴期望电流iderf通过电压外环控制器得到。内环控制器的作用是跟踪逆变器输出三相电流和直流侧电容电压。
4 仿真与比较
4.1 双环控制仿真
根据以上分析, 在MATLAB/Simlink仿真软件中搭建基于Lyapunov函数的T型三电平并网逆变器控制策略仿真模型。仿真模型参数如表 2所示。表 2中, Lf和Cf分别为滤波电感和滤波电容; α1和β1为控制增益; fs为逆变器的开关频率; f为电网频率。
表 2
仿真模型参数设置
| Udc/V | fs/kHz | C1 | C2 | Cf | Lf/mH |
| μF | |||||
| 600 | 2.5 | 3 300 | 3 300 | 50 | 5 |
| α1 | β1 | uea | ueb | uec | f/Hz |
| V | |||||
| -0.015 | -0.015 | 311 | 311 | 311 | 50 |
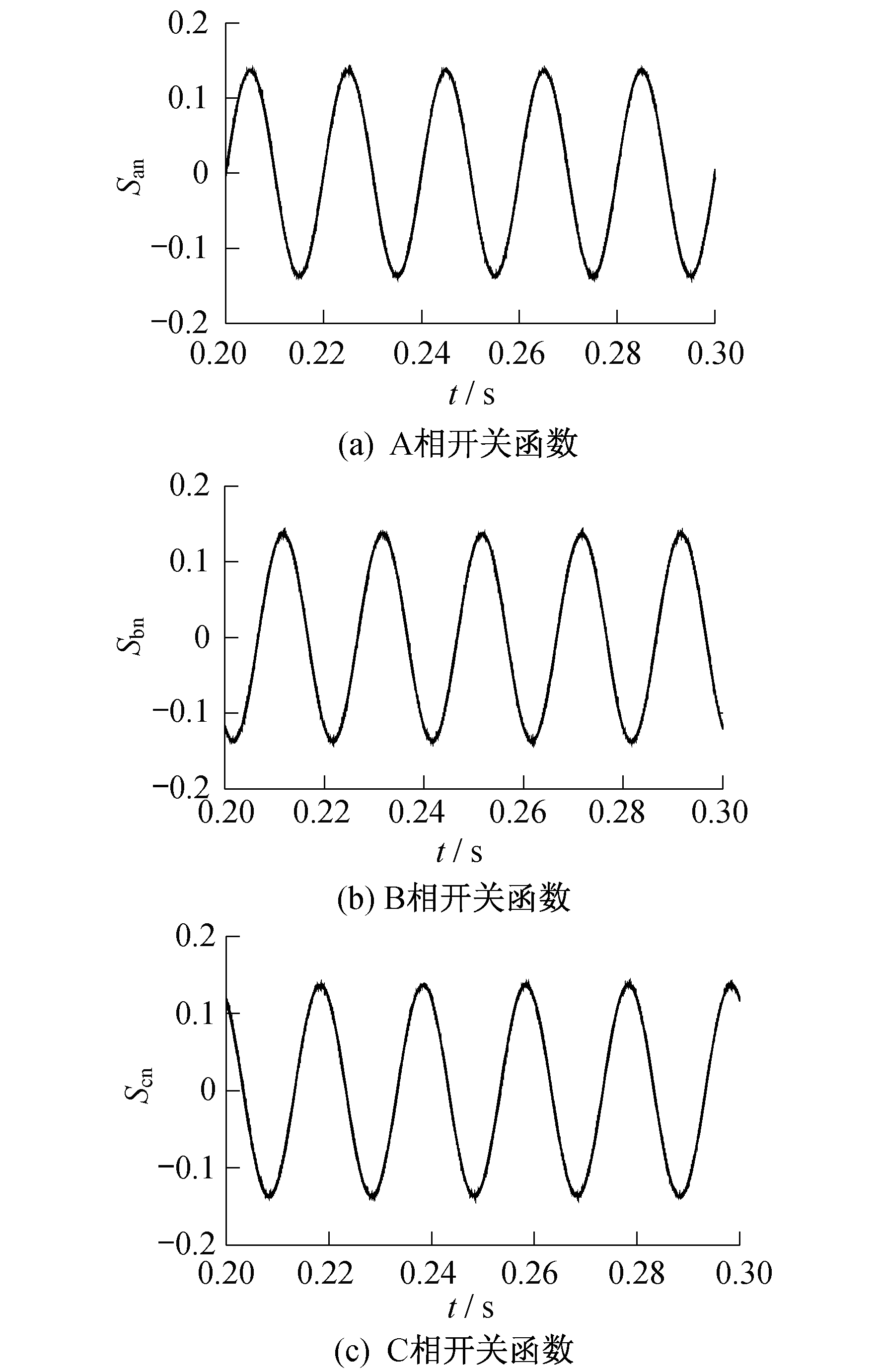
图 4为电流内环Lyapunov函数输出的开关函数Sd1, Sd4, Sq1, Sq4经dq-abc坐标变换得到的abc三相开关函数波形。由图 4可知, 三相开关函数在相位上相差120°, 幅值相等, 因此可作为SVPWM调制算法的输入, 驱动逆变器桥臂开关动作。
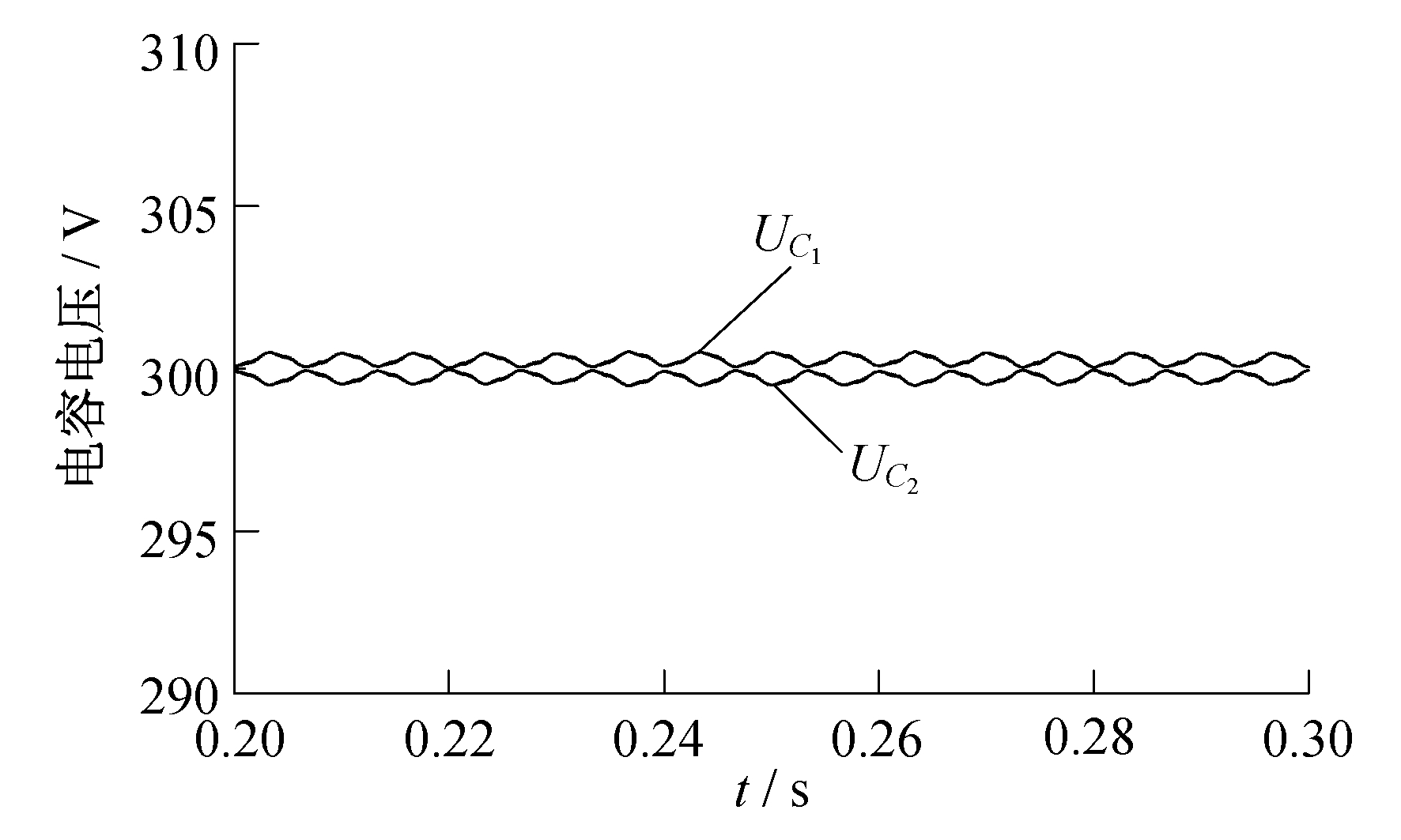
图 5为直流侧电容电压。由图 5可知, 上下电容电压偏移不到±1 V, 即中性点电位偏移问题小。由此验证了本文提出的双环控制策略可以有效抑制中性点的电位偏移。
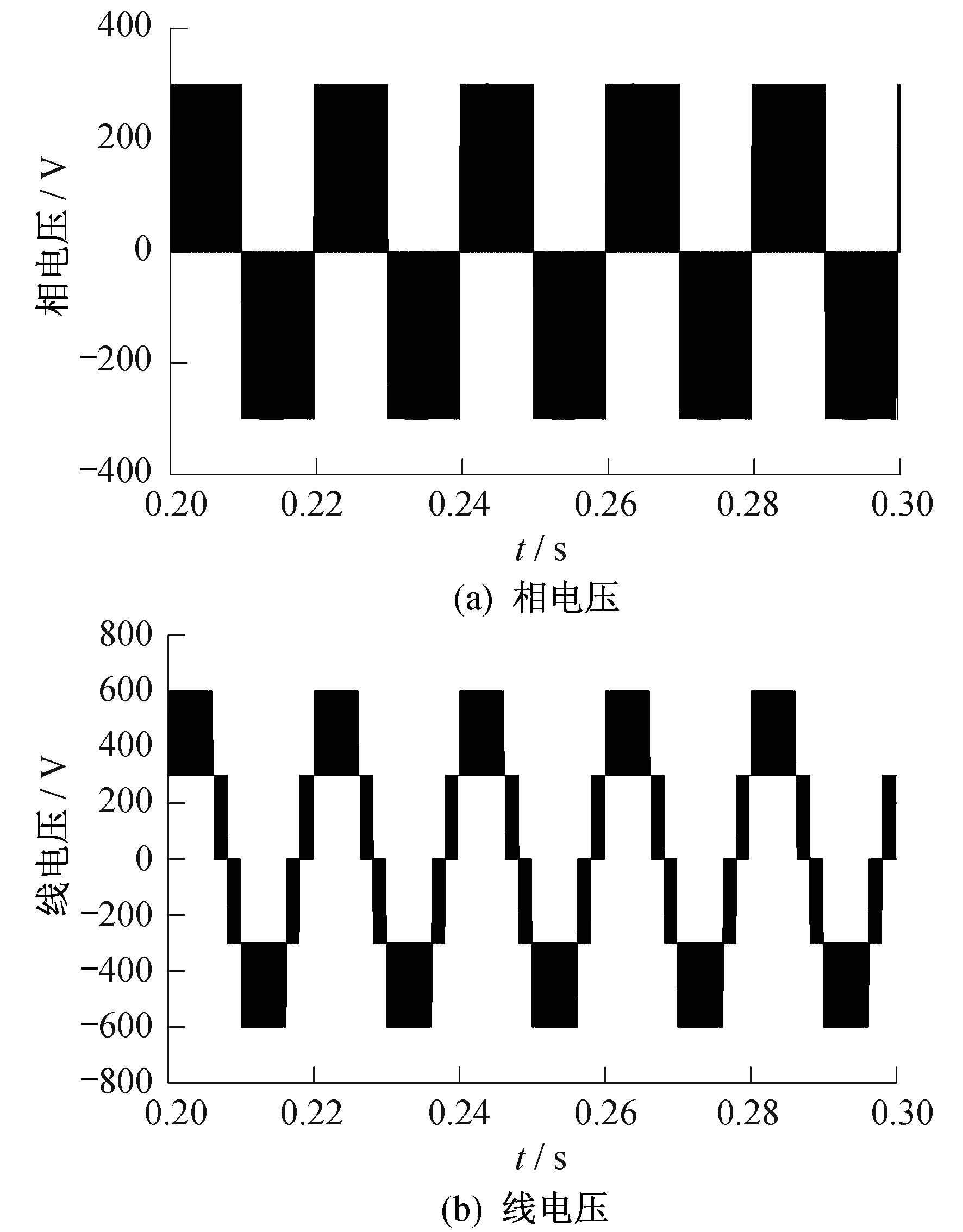
图 6为逆变器输出相电压与线电压波形。由图 6可知, 逆变器输出相电压为±300 V和0 V共3种电平, 输出线电压为±600 V, ±300 V, 0 V共5种电平, 这与逆变器理论输出的相电压与线电压电平数相一致。
4.2 与传统双PI控制比较
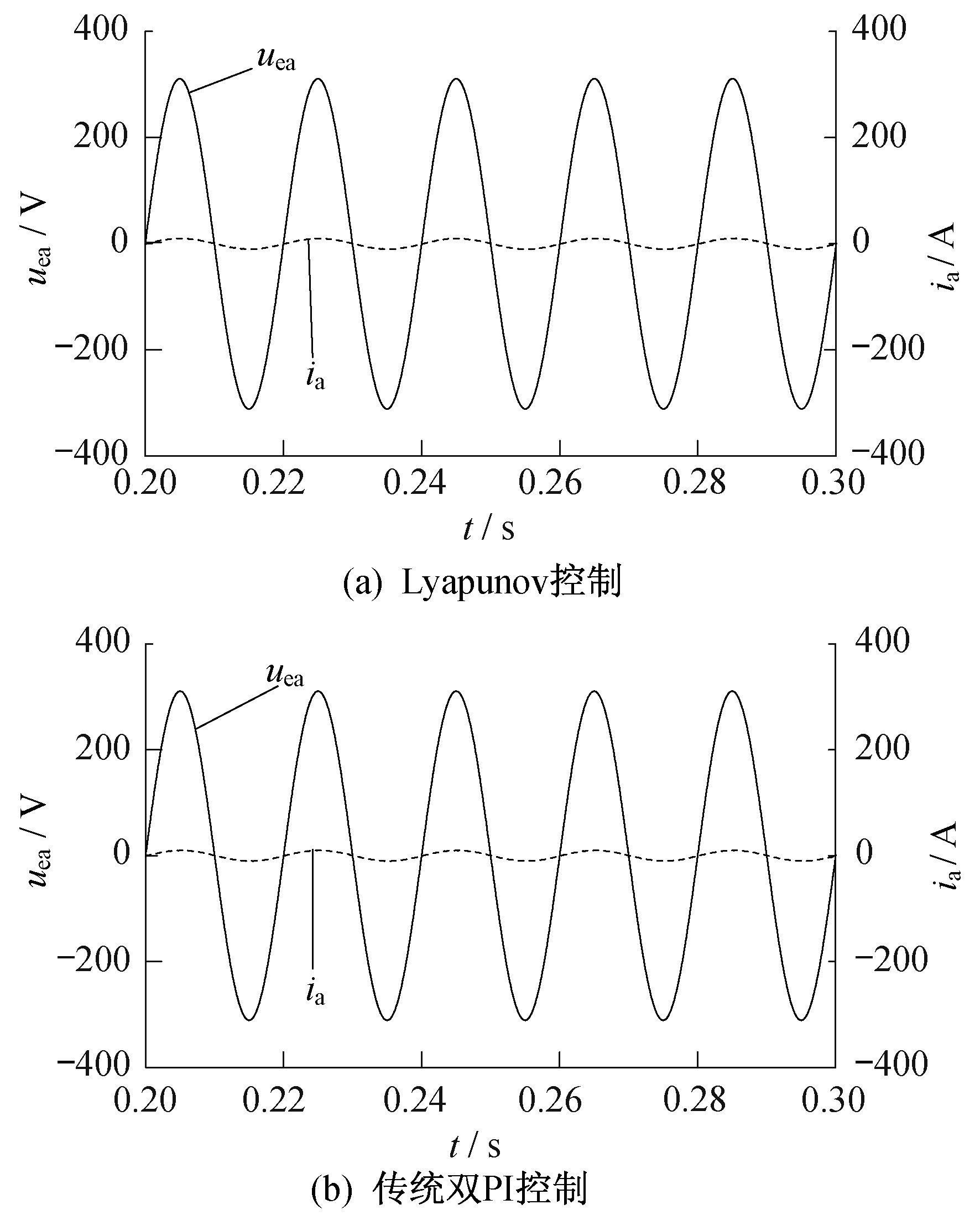
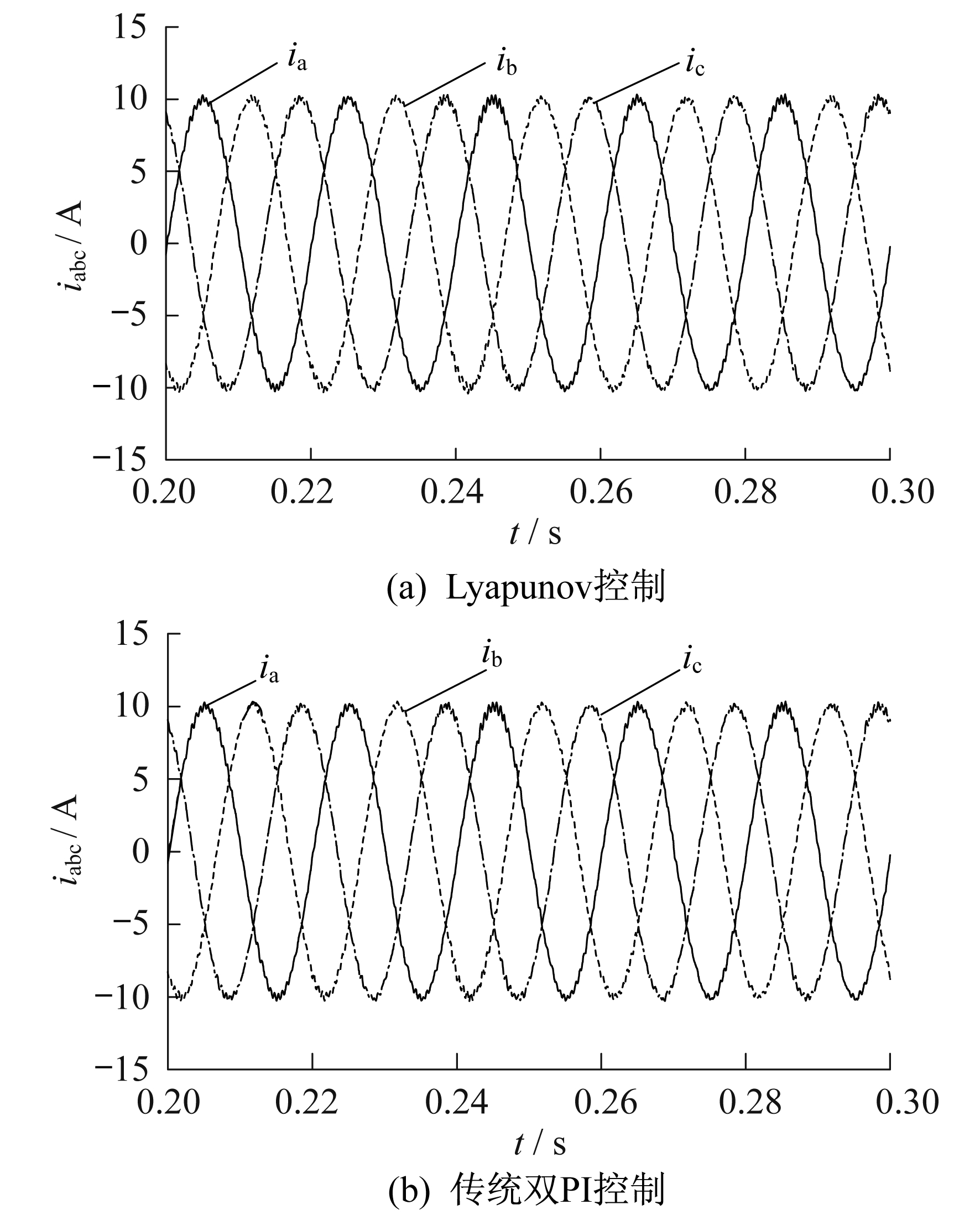
传统的电压-电流双环控制策略的外环与内环均采用PI控制。为了突出本文所提双环控制系统的优势, 将其与传统的双环控制系统进行对比。在传统的双环控制系统中, 电压外环控制器采用PI控制, 比例系数、积分系数分别为Kp=0.8, Ki=5;而电流内环控制器采用P控制, 比例系数为Kp=20。图 7为两种控制策略下A相并网电压与电流波形。图 8为两种控制策略下逆变器输出三相电流波形。
由图 7可知, 两种控制策略都可以实现较高功率因数并网。由图 8可知, 采用Lyapunov函数控制时, 逆变器输出三相电流波形比较平滑, 即输出电流谐波较低, 可以表明上述理论部分提出的电流内环控制策略可以实现电流谐波跟踪。
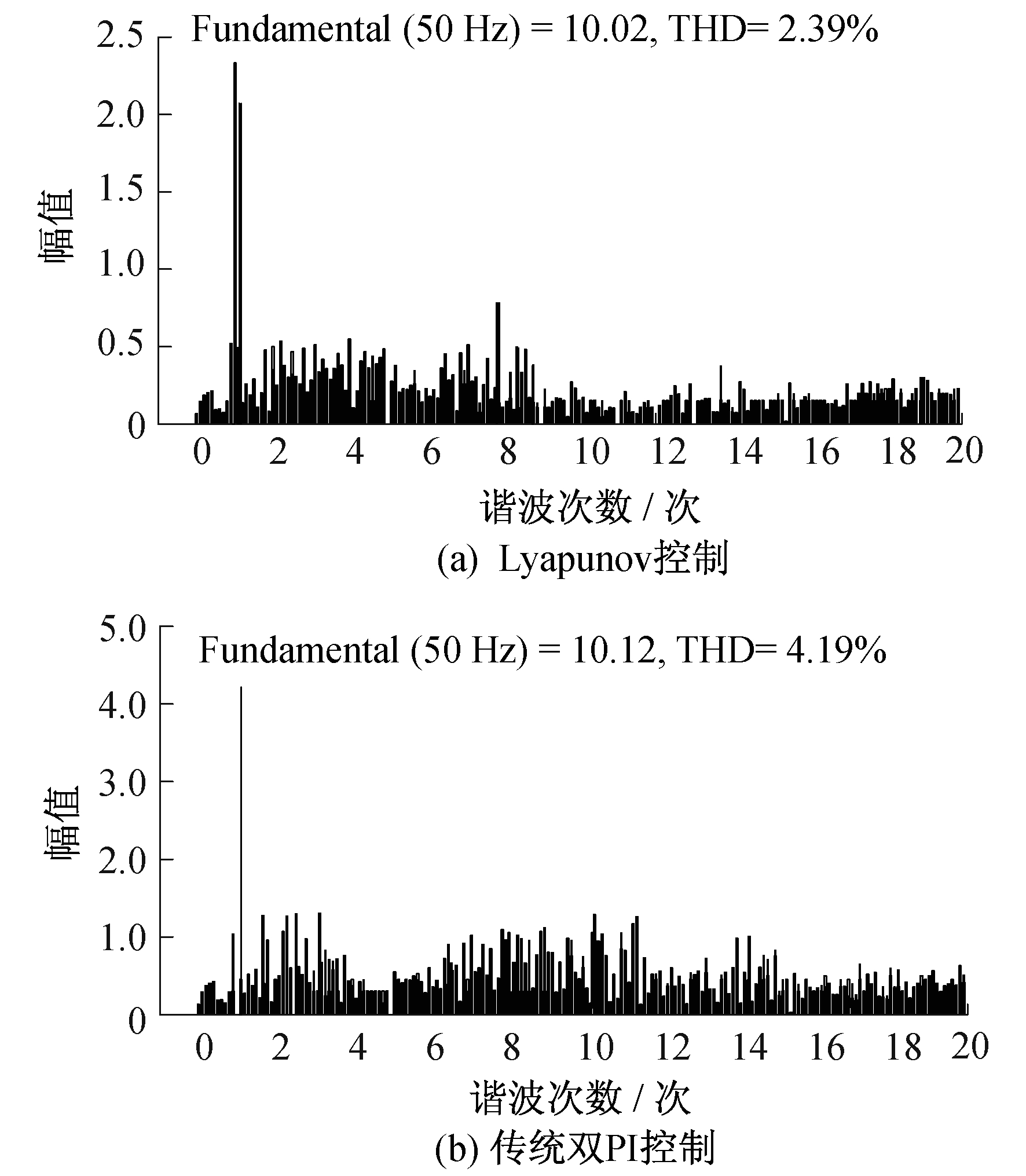
图 9为两种控制策略下逆变器输出A相电流谐波。
由图 9可知, Lyapunov控制与双PI控制输出总谐波畸变率依次为2.39%和4.19%。由此验证采用Lyapunov控制可以有效抑制电流谐波、提高电能输出质量这一论点。
5 结论
本文提出了一种新型电压-电流双环控制策略, 其中电流内环采用Lyapunov函数控制, 用以实现对三相并网电流谐波的跟踪; 电压外环采用传统的PI控制, 以实现对中性点电容电压的跟踪。仿真得出以下结论:
(1) 本文将Lyapunov函数方法应用到T型逆变器电流内环控制, 能够有效抑制中性点的电位偏移;
(2) 与传统的双PI控制策略相比, 本文提出的控制策略能够有效跟踪电流谐波, 提高电能的输出质量。
参考文献
-
[1]分布式发电系统电网同步锁相技术[J]. 中国电机工程学报, 2013, 33(1): 50-55.
-
[2]基于准PR调节器电流双闭环LCL三相并网逆变器控制[J]. 电力系统保护与控制, 2014, 42(12): 44-50. DOI:10.7667/j.issn.1674-3415.2014.12.008
-
[3]基于E-L模型的Z源T型逆变器无源控制策略研究[J]. 电网技术, 2018, 42(7): 2303-2311.
-
[4]电压源逆变器典型控制方法的电路本质分析[J]. 中国电机工程学报, 2016, 36(18): 4980-4989.
-
[5]三相并网逆变器比例谐振控制及其网压前馈问题分析[J]. 电工技术学报, 2012, 27(8): 56-63.
-
[6]T型三电平并网逆变器的准PR控制系统研究[J]. 广东电力, 2018, 31(3): 86-91.
-
[7]Z源光伏并网逆变器无差拍解耦控制[J]. 电网技术, 2012, 36(3): 252-256.
-
[8]LCL并网逆变器新型电流双闭环控制策略研究[J]. 电力系统保护与控制, 2012, 40(17): 1-5. DOI:10.7667/j.issn.1674-3415.2012.17.001
-
[9]基于准Z源逆变器的光伏发电系统的双滑模变结构控制[J]. 上海电力学院学报, 2017, 33(5): 459-465.
-
[10]基于李雅普诺夫函数的并联型混合有源电力滤波器非线性控制方法[J]. 电工技术学报, 2016, 31(21): 133-141. DOI:10.3969/j.issn.1000-6753.2016.21.015
-
[11]基于Lyapunov函数的混合型有源电力滤波器控制策略[J]. 控制理论与应用, 2014, 31(9): 1174-1181. DOI:10.7641/CTA.2014.30776
-
[12]基于Lyapunov函数的NPC型SAPF非线性控制策略[J]. 电力系统自动化, 2018, 42(11): 143-149. DOI:10.7500/AEPS20170929006
-
[13]KOMURCUGIL H, ALTIN N, OZDEMIR S, et al. Lyapunov-function and proportional-resonant-based control strategy for single-phase grid-connected VSI with LCL filter[J]. IEEE Transaction on Industrial Electronics, 2016, 63(5): 2838-2849. DOI:10.1109/TIE.2015.2510984