|
|
|
发布时间: 2019-10-10 |
|
|
|
|
收稿日期: 2019-04-02
中图法分类号: TP391.4
文献标识码: A
文章编号: 1006-4729(2019)05-0442-07
|
摘要
针对核相关滤波算法仅使用一种特征表达进行目标追踪, 使其在一些场景中跟踪效果不佳的问题, 提出了一种多特征融合的核相关滤波跟踪方法。采用31维的方向梯度直方图特征、58维的局部二值模式特征和1维的灰度特征进行融合。该算法选择在特征层进行特征融合, 先将方向梯度特征和局部二值模式特征并联融合, 再将融合后的特征串联融合灰度特征, 形成新的特征表达。在OTB(Object Tracking Benchmark)数据集上进行了测试, 结果表明, 该算法具有更好的跟踪效果。
关键词
核相关滤波; 特征融合; 目标跟踪
Abstract
A kernel correlation filtering method based on multi-feature fusion is proposed for the kernel correlation filtering algorithm using only one feature expression for target tracking, which makes the tracking effect of the algorithm in some scenes poor.The 31-dimensional histogram of oriented gradient feature, the 58-dimensional local binary patterns feature and the 1-dimensional gray feature are used for fusion.The algorithm selects the feature fusion in the feature layer, combining the histogram of oriented gradient feature and the local binary mode feature.Then, the fused features are fusing into the gray feature to form a new feature expression.The improved algorithm is tested on the Object Tracking Benchmark(OTB) dataset.Experiments show that the algorithm has better effect on tracking.
Key words
kernelized correlation filter; feature fusion; target tracking
计算机视觉是所有从二维图片中获得情景信息的计算机处理方法的总称[1]。目标跟踪是国内外计算机视觉领域的研究热点[2-3], 在机器人、视频监控、人机交互和无人驾驶等领域应用广泛。通常目标在视频或图像序列中存在着外观变形、尺度变化、光照变化、快速旋转运动、背景相似干扰和视野丢失等现象[4-5]。这些现象的存在, 使得目标跟踪具有一定的难度。研究人员针对不同的问题提出了不同的解决方法。这些方法可以分为两大类:一是生成类方法, 二是判别类方法。生成类方法是在前一视频帧的目标区域建模, 在当前帧寻找与模型最相似的区域; 判别类方法是在前一视频帧的目标区域和背景区域中提取正负样本进行训练, 从而得到一个目标分类器, 利用训练好的目标分类器找到待检测目标的位置。
基于相关滤波(Correlation Filtering, CF)的跟踪方法属于判别类方法[6]。CF方法的跟踪性能良好, 计算效率极高, 能够跟踪较复杂的目标, 是目标跟踪领域的研究热点之一。在跟踪过程中, CF方法通过前一帧的训练数据集训练分类器, 利用训练好的分类器跟踪当前帧的目标, 同时更新分类器。HENRIQUES J F等人[7-8]将核函数引入误差最小平方和滤波(Minimum Output Sum of Squared Error, MOSSE)算法, 提出了基于循环结构核(Circulant Structure Kernels, CSK)算法, 并在该算法的基础上改进得到了核相关滤波(Kernelized Correlation Filters, KCF)算法。KCF算法加入了多通道方向梯度直方图(Histogram of Oriented Gradient, HOG)特征, 提高了跟踪器的跟踪精度。但当跟踪的目标外观发生变化时, 仅利用图像的单一特征进行跟踪会产生模型误差, 从而影响目标跟踪的稳健性。
针对上述问题, 本文在KCF算法的基础上, 提出了一种多特征融合的核相关滤波跟踪方法。从特征融合入手, 将优缺点可以互补的特征进行融合, 同时在数据集上进行实验, 以验证改进算法的跟踪性能。
1 KCF跟踪算法
1.1 循环矩阵
KCF算法是利用循环矩阵构造训练样本。假设基础样本x是一组1×n维的向量[x1, x2, x3, …, xn], 通过循环移位可以得到样本矩阵X, 表示为
| $ \boldsymbol{X}=C(\boldsymbol{x})=\left[\begin{array}{ccccc} x_{1} & x_{2} & x_{3} & \cdots & x_{n} \\ x_{n} & x_{1} & x_{2} & \cdots & x_{n-1} \\ x_{n-1} & x_{n} & x_{1} & \cdots & x_{n-2} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ x_{2} & x_{3} & x_{4} & \cdots & x_{1} \end{array}\right] $ | (1) |
其中矩阵X的第一行为向量x, 其他各行是向量x向右移动1, 2, 3, …n-1位得到的样本。文献[7]表明, 所有的循环矩阵都能够在傅里叶域使用离散傅里叶矩阵进行对角化, 即
| $ \boldsymbol{X}=\boldsymbol{F} \operatorname{diag}(\hat{\boldsymbol{x}}) \boldsymbol{F}^{\mathrm{H}} $ | (2) |
式中:F——离散傅里叶矩阵;
FH——F的复共轭的转置;
∧——离散傅里叶变换。
1.2 目标分类器
样本训练是为了找到一个函数f(xi)=wTxi, 让样本xi与其对应的yi的均方误差最小。
| $\underset{w}{\min } \sum\limits_{i}\left(f\left(x_{i}\right)-y_{i}\right)^{2}+\lambda\|w\|^{2}$ | (3) |
式中的λ是正则化参数, 其作用是提高分类器的泛化能力, 防止过度拟合。
由线性最小二乘法解得
| $\boldsymbol{w}=\left(\boldsymbol{X}^{\mathrm{H}} \boldsymbol{X}+\lambda \boldsymbol{I}\right)^{-1} \boldsymbol{X}^{\mathrm{H}} \boldsymbol{y}$ | (4) |
利用循环矩阵的特性, 将式(2)代入式(4)中, 再进行离散傅里叶变换, 可得
| $ \hat{\boldsymbol{w}}=\frac{\hat{\boldsymbol{x}}^{*} \odot \hat{\boldsymbol{y}}}{\hat{\boldsymbol{x}}^{*} \odot \hat{\boldsymbol{x}}+\lambda} $ | (5) |
式中, ⊙表示向量对应元素做乘积运算, 求解w只需将 进行傅里叶反变换。
进行傅里叶反变换。
以上是线性岭回归问题。对于非线性分类问题, 目标函数转化为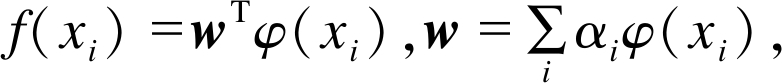 样本训练转化为对α的求解, 由式(4)可得
样本训练转化为对α的求解, 由式(4)可得
| $\boldsymbol{\alpha}=(\boldsymbol{K}+\lambda \boldsymbol{I})^{-1} \boldsymbol{y}$ | (6) |
若K也为循环矩阵, 即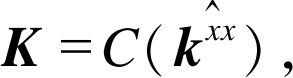 表示K是由
表示K是由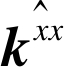 循环移位所得, 且
循环移位所得, 且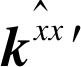 是核矩阵K的第一行。它仍具有式(2)的性质, 最终可解得
是核矩阵K的第一行。它仍具有式(2)的性质, 最终可解得
| $ \hat{\boldsymbol{\alpha}}=\frac{\hat{\boldsymbol{y}}}{\boldsymbol{k}^{\hat{x} x}+\lambda} $ | (7) |
对于待检测样本z, 其对应的回归值为
| $ f(z)=\boldsymbol{w}^{\mathrm{T}} z=\sum\limits_{i=1}^{n} \alpha_{i} k\left(z, x_{i}\right) $ | (8) |
当待检测样本z数量较多时, 采用循环矩阵构造检测样本。定义训练样本和检测样本的核矩阵为
| $\boldsymbol{K}^{Z}=C\left(\boldsymbol{k}^{x z}\right)$ | (9) |
结合式(8)和式(9)可得
| $f(z)=\left(\boldsymbol{K}^{Z}\right)^{\mathrm{T}} \boldsymbol{\alpha}$ | (10) |
为了提高计算速度, 将式(10)转化到傅里叶域计算, 此时目标函数可以表示为
| $ \hat{f}(z)=\boldsymbol{k}^{\hat{\lambda} z} \odot \hat{\boldsymbol{\alpha}} $ | (11) |
跟踪目标对应的位置, 就是目标函数的最大响应值, 详细的算法计算过程可以参考文献[8]。
2 KCF算法改进
2.1 特征介绍
在跟踪算法中, 特征表达的是否有效直接决定跟踪结果的好坏。为了平衡特征表达能力和计算复杂度, 在KCF算法的基础上提出了融合具有相互互补性的特征。在不同的跟踪场景中, 不同的特征对目标的描述各有侧重, 本文主要介绍灰度特征、HOG特征和局部二值模式(Local Binary Patterns, LBP)特征。
2.1.1 灰度特征
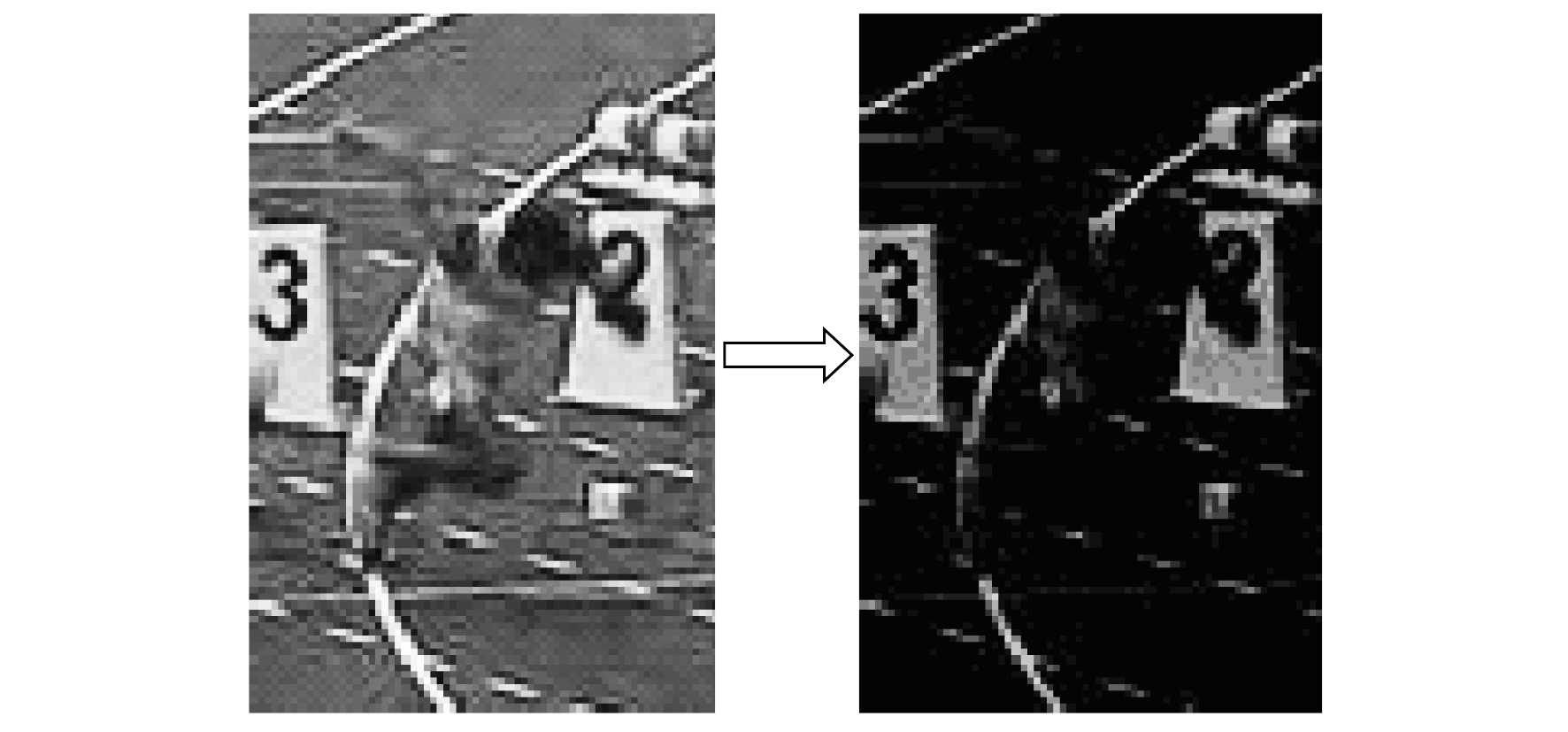
灰度(Gray)特征是跟踪算法中使用较早的一种特征, 例如在MOSSE算法和CSK算法中均采用了灰度特征进行目标描述。灰度特征是先将原始图像转化为灰度图, 然后对灰度值进行归一化, 使得光照变化对该特征的影响减弱。灰度特征如图 1所示。
2.1.2 HOG特征
2.1.3 LBP特征
2.2 特征融合可行性分析
灰度特征只有一维, 便于与其他特征融合; 同时它计算简单、复杂度较低, 可以最大程度地描述目标本身的状态。当图像目标尺寸较小或图像的分辨率较低时, 计算过程复杂的特征描述子并不能够完全描述目标, 这时采用灰度特征可以改善跟踪效果。
HOG特征属于局部形状特征, 对光照影响和几何形变不敏感, 计算复杂度也较低, 符合实时目标跟踪的要求。当跟踪场景中有形变、光照变化以及局部遮挡发生时, 利用HOG特征跟踪目标效果良好。在目标和背景颜色相近、目标边缘或者背景有噪声的场景中, HOG特征和灰度特征无法有效地描述目标, 此时则可以利用纹理特征对跟踪目标进行补充描述。LBP特征的描述方法与HOG特征相似, 易与HOG特征融合。
2.3 特征融合
多特征融合需要融合的特征对目标的描述有互补性, 还要有相似的计算过程。由上述介绍可知, 3种特征在不同的场景中对目标的跟踪各有优劣, 三者之间存在一定的互补性且将这3种特征进行融合是可行的。
针对HOG特征, 本文采用的是快速Felzenszwalb’s HOG特征[12]。该特征将梯度方向分为9个, 利用9个方向通道的直方图计算HOG特征。其中, 有2×9维方向通道的对比度敏感, 有1×9维的方向通道的对比度不敏感, 还有1×4维的纹理通道。因此, 本文采用的HOG特征的总维数是18+9+4=31维。
针对LBP特征, 本文采用的是LBP算子的等价模式。对于标准LBP特征, 将其二进制数串记为首尾循环, 若其中从0到1或者从1到0跳变次数小于等于两个, 则称该局部二进制模式为等价模式[13]。利用等价模式, LBP算子就可以从原始的256种减少到58种, 其特征维数就可以降为58维。
通常, 按照融合系统中数据抽象的层次, 图像融合可以划分为像素级融合﹑特征级融合和决策级融合3个级别[14]。文献[15]指出, 采用特征级图像融合方法描述所识别的性能要优于像素级图像融合和决策级图像融合。特征融合的方法一般有串联融合和并联融合两种。串联融合后形成新的特征矩阵, 此时特征矩阵的维数为特征向量维数相加; 并联融合后形成的新特征矩阵维数为特征向量中维数的最大值。当需要融合的特征向量维数较多时, 串联融合会使融合后的新特征向量维数也较多, 会加大需计算的特征通道数, 进而影响算法的跟踪速度。并联融合不会增加需计算的特征通道数, 但要求融合的特征向量之间具有相似的特征维数, 从待融合特征本身而言, 待融合的特征还需有相似的表达方式和归一化的表达空间。
在3种待融合特征中, HOG特征和LBP特征具有相似的特征表达方式。HOG特征(31维)和LBP特征(58维)特征维数相似, 若这两者之间采用串联融合, 算法需计算的特征通道就会增加, 所以串联融合不适用于这两种特征的融合, 应采用并联融合。灰度特征只有一维, 采用串联融合不会给其他特征造成特征维数的负担。相比于其他融合方式, 串联融合和并联融合较为常见且易于编程实现。本文先将HOG特征(31维)和LBP特征(58维)并联融合, 再串联融合灰度特征, 融合后的特征为HLG(HOG+LBP+Gray)特征(59维)。特征层融合的方法如图 4所示。
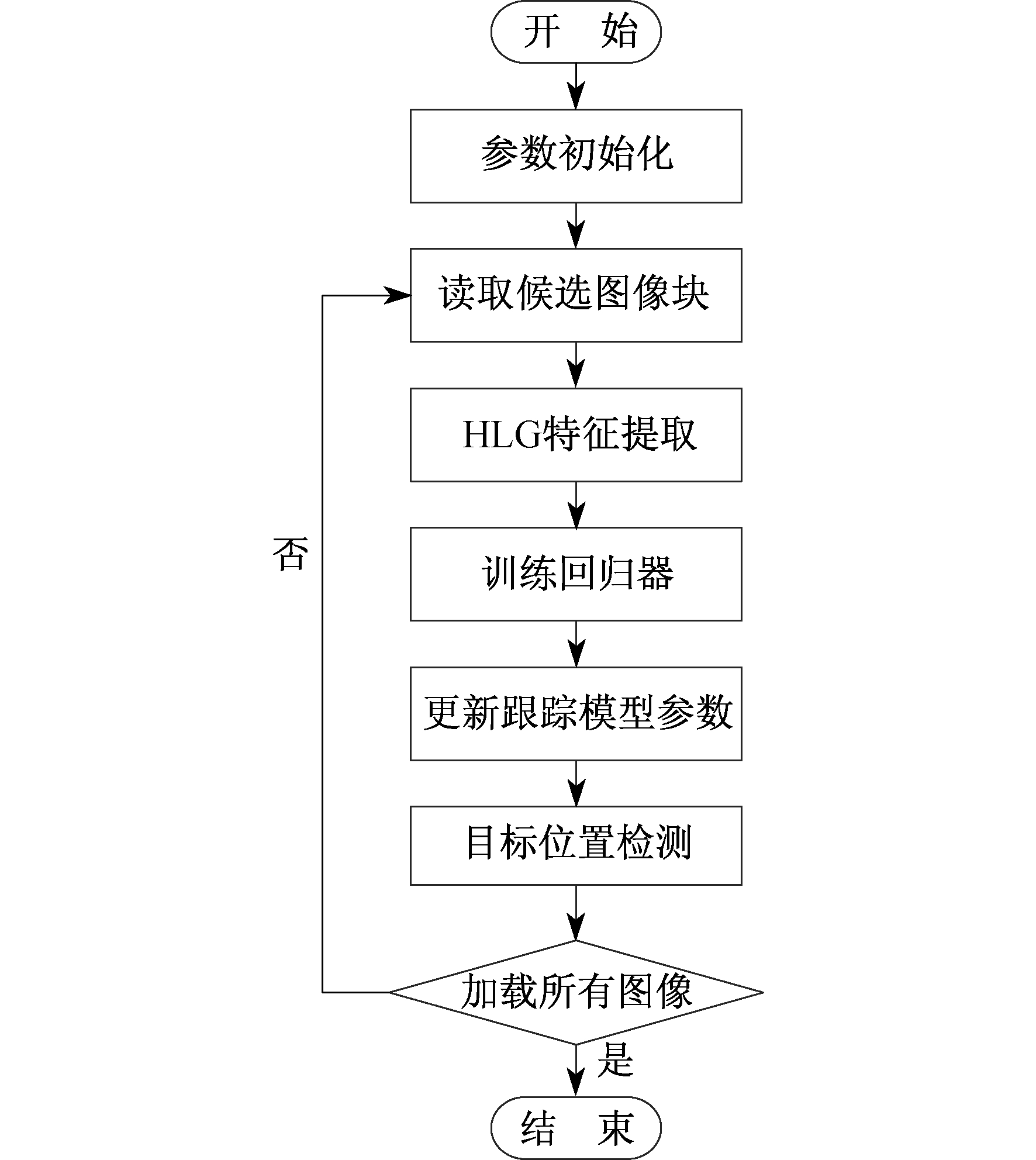
改进的KCF算法首先从输入的视频帧中读取候选图像块, 将融合好的HLG特征进行特征提取, 然后训练分类器, 通过训练好的分类器检测出目标的位置, 最后更新跟踪模型的参数。改进的KCF算法流程如图 5所示。
改进算法的详细步骤如下。
步骤1 参数初始化。从数据集中读入第一帧和跟踪目标的初始位置pos, 创建跟踪目标框并将跟踪框的大小扩大为2.5倍, 大小记为M×N, 同时对跟踪框进行余弦加权。
步骤2 样本训练。首先利用新融合的HLG特征提取目标特征, 得到59维的特征图。每个特征维度的样本输入记为x1, x2, x3, …, x59, 其大小是M×N; 然后将提取到的特征转化到傅里叶域, 通过高斯函数生成与样本大小M×N一致的训练矩阵Y; 最后通过式(7)训练出非线性回归器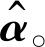
步骤3 模型和参数更新。利用公式αn=(1-β)×αn-1+β×newαn更新参数得到新的model_alphaf, 利用公式 更新滤波器模板得到新的model_xf。
更新滤波器模板得到新的model_xf。
步骤4 样本检测。先提取下一帧图像的HLG特征, 再通过步骤3中更新的model_xf计算检测核相关矩阵, model_alphaf计算响应值。找到响应值中最大的值, 即为跟踪的目标位置。重复步骤2到步骤4, 直到所有的图像序列加载完成。
3 实验结果及分析
3.1 定性分析
本实验的数据集采用的是文献[4]提出的OTB(Object Tracking Benchmark)数据集。OTB数据集中的视频序列包含了光照变化、尺度变化、遮挡、目标变形、目标运动模糊、目标快速移动、目标平面内旋转、目标超平面旋转、目标离开视野、背景杂乱和低分辨率等不同的运动场景。通过灰度特征、LBP特征、HOG特征和新合成的HLG特征, 选取数据集中较为典型的Basketball, Skating1, Shaking, Tiger2, Couple, Freeman4序列进行了跟踪。利用灰度特征跟踪目标的实验结果如图 6所示。LBP特征跟踪目标的实验结果如图 7所示。HOG特征和HLG特征跟踪目标的实验结果如图 8所示。
由图 6可以看出, 图 6(a)中跟踪框出现漂移现象; 图 6(b)中由于目标和背景太过接近, 跟踪框无法确定目标的准确位置; 图 6(c)和图 6(d)中出现了目标丢失的情况; 图 6(e)中的跟踪较好; 图 6(f)中出现了短暂的目标丢失, 但最终仍能实现对目标的跟踪。由图 6(e)和图 6(f)可以看出, 灰度特征在跟踪目标较小、目标在平面内快速移动的场景中跟踪效果较好。
由图 7可以看出, 图 7(a)和图 7(b)、图 7(e)和图 7(f)序列中都出现了目标丢失的情况, 跟踪效果不佳, 但在图 7(c)和图 7(d)序列中的跟踪效果较佳, 在目标跟踪的过程中没有出现目标丢失和跟踪框的漂移。可见LBP特征在背景复杂、光照变化强烈、有部分遮挡的场景中可以很好地跟踪到目标。
图 8中每组序列的上面一行是HOG特征的跟踪效果, 下面一行是新合成的HLG特征的跟踪效果。由于原算法采用的是HOG特征, 故将HOG特征和HLG特征的跟踪效果进行对比。由图 8可以看出, HLG特征的跟踪效果要优于HOG特征的跟踪效果。由图 6和由图 7可以看出, LBP特征和灰度特征均不能很好地实现实时跟踪, 都存在一定的缺陷。由此可知, 相较于单一的特征, 融合后的特征能够适应在更多的场景中进行跟踪, 且跟踪效果较好, 弥补了原算法仅使用单一特征跟踪目标的缺陷。
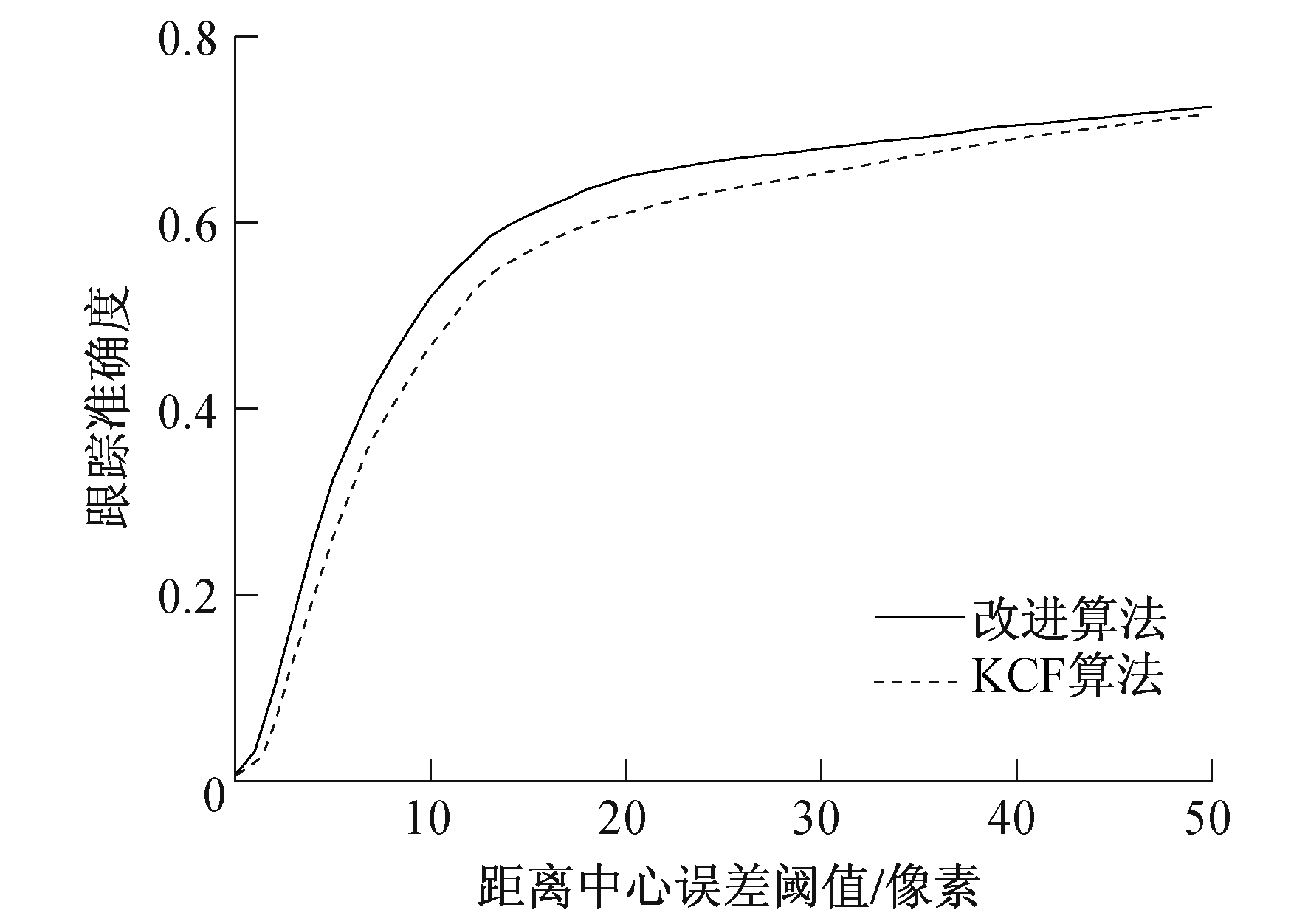
3.2 定量分析
4 结语
本文提出的多特征融合的核相关滤波跟踪算法, 较好地克服了目标尺度变化、光照变化、目标形变等挑战属性; 利用融合后的特征表达, 在具有挑战性的场景中对目标进行跟踪, 获得了较好的跟踪效果。由于本文所提算法计算速度快、编程简单、易于实现, 所以能够适用于更多场景中对目标的实时跟踪。本文算法的不足之处是目标尺度无法实现自适应的变化, 今后可以从目标尺度自适应的方向进行改进, 以增加目标跟踪的准确率。
参考文献
-
[1]计算机视觉原理分析及其应用[J]. 上海电力学院学报, 2016, 32(3): 283-287.
-
[2]ZHANG T Z, XU C C, YANG M H. Multi-task correlation particle filter for robust object tracking[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, Hawaii, 2017: 4819-4827.
-
[3]目标跟踪算法综述[J]. 模式识别与人工智能, 2018, 31(1): 61-76.
-
[4]WU Y, LIM J, YANG M H. Online object tracking: a benchmark[C]//Proceedings of 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 2013: 2411-2418.
-
[5]SMEULDERS A W M, CHU D M, CUCCHIARA R, et al. Visual tracking: an experimental survey[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(7): 1442-1468. DOI:10.1109/TPAMI.2013.230
-
[6]特征融合的尺度自适应相关滤波跟踪算法[J]. 光学学报, 2019, 42(3): 0515001.
-
[7]HENRIQUES J F, CASEIRO R, MARTINS P, et al. Exploiting the circulant structure of tracking-by-detection with kernels[C]//FITZGIBBON A, LAZEBNIK S, PERONA P, et al. Computer Vision-ECCV 2012. Lecture Notes in Computer Science, Berlin, Heidelberg: Springer, 2012: 715-720.
-
[8]HENRIQUES J F, CASEIRO R, MARTINS P, et al. High-speed tracking with kernelized correlation filters[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596. DOI:10.1109/TPAMI.2014.2345390
-
[9]基于LBP和HOG特征分层融合的步态识别[J]. 计算机工程与应用, 2018, 54(24): 168-175. DOI:10.3778/j.issn.1002-8331.1806-0009
-
[10]采用HOG特征和机器学习的行人检测方法[J]. 华侨大学学报, 2018, 39(5): 768-773.
-
[11]一种改进的LBP特征实现铁路扣件识别[J]. 西南交通大学学报, 2018, 53(5): 893-899. DOI:10.3969/j.issn.0258-2724.2018.05.003
-
[12]FELZENSZWALB P F, GIRSHICK R B, MCALLESTER D, et al. Object detection with discriminatively trained part-based models[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(9): 1627-1644. DOI:10.1109/TPAMI.2009.167
-
[13]严小乐.基于相关滤波的视频运动目标跟踪算法研究[D].南京: 南京航空航天大学, 2017.
-
[14]面向目标识别的多特征图像融合技术综述[J]. 航空电子技术, 2011, 42(2): 6-12. DOI:10.3969/j.issn.1006-141X.2011.02.002
-
[15]韩崇昭, 朱洪艳, 段战胜, 等.多源信息融合[M].北京: 电子工业出版社, 2007.
-
[16]基于改进核相关滤波器的目标跟踪算法[J]. 计算机工程, 2018, 44(11): 222-227.