|
|
|
发布时间: 2019-10-10 |
|
|
|
|
收稿日期: 2019-04-02
基金项目: 电网本质安全框架设计与管控研究(H2018-184)
中图法分类号: TM08
文献标识码: A
文章编号: 1006-4729(2019)05-0449-06
|
摘要
在电网本质安全评价过程中, 确定评价指标的权重是一个必要的环节, 权重值的大小将直接影响评价结果。根据所构建的评价指标体系, 运用层次分析法(AHP)来确定主观权重, 运用粗糙集(RS)理论来确定客观权重, 并通过最小相对信息熵原理将二者进行组合, 得到兼顾专家经验和客观信息的评价指标权重。实例应用表明, 该组合赋权法更加合理有效, 实用性更强。
关键词
电网; 本质安全评价; 指标权重; 层次分析法; 粗糙集
Abstract
In the process of intrinsic safety evaluation of power grids, determining the weight of evaluation indicators is a necessary link, and the weight value will directly affect the evaluation results.According to the constructed evaluation index system, the Analytic Hierarchy Process (AHP) is used to determine the subjective weights, and the Rough Set(RS) theory is used to determine the objective weights, and combine the two by the principle of minimum relative information entropy to get the weight that takes into account the expert experience and objective information.The example application shows that the combination weighting method is more reasonable, more effective and more practical.
Key words
power grid; Intrinsic safety evaluation; index weight; analytic hierarchy process; rough set
电力企业作为关乎国家安全和国民经济命脉的国有重点能源企业, 是我国经济发展的基石, 并且电能生产及使用具有的实时特性使得电力企业的生产安全尤为重要, 因此对电力企业进行本质安全评价非常必要。评价指标权重的确定是评价过程中的一个关键环节, 有多种确定方法。根据其计算时原始数据的来源和计算过程的不同, 主要分为主观赋权法、客观赋权法和主客观赋权法[1-2]3大类别。其中:主观赋权法是由专家主观上对各属性的重视程度来确定属性权重, 如专家调查法、层次分析法(Analytic Hierarchy Process, AHP)等; 客观赋权法主要依靠样本数据分析计算权重, 如主成分分析法、粗糙集(Rough Set, RS)法等; 组合赋权法即为主观赋权法和客观赋权法的组合, 组合方式较多, 可使属性的权重同时兼顾专家经验和客观信息。
AHP作为主观赋权法的一种, 在计算过程中既能保证定量分析的优势, 又能结合定性分析的结果, 使得评估过程的条理性较强, 计算简便, 应用范围广泛[3-4]; RS法作为客观赋权法的一种, 其处理的数据类型广泛, 具有较强的容错能力, 对数据处理的准确度较高, 速度较快。因此, 本文将这两种方法进行组合, 由AHP计算得主观权重、RS法计算得客观权重, 以使评价指标的权重在主观和客观上得到较好的统一。
1 基于AHP-RS的指标权重确定
1.1 AHP确定指标主观权重
1.1.1 建立层次结构模型
通过对系统的深刻认识, 全面收集信息后建立多层次的递阶结构, 按准则的要求、决策功能的不同等, 将系统分为几个层次。
1.1.2 构造两两比较判断矩阵
在递阶结构中, 将属于上一层同一指标的同层指标进行两两比较, 比较其对于上层指标的重要程度, 并按规定好的标度量化构成判断矩阵。例如指标a1, a2, a3从属于上层指标ak, 则其构造的判断矩阵如表 1所示。
表 1
判断矩阵构造
| $a_{k}$ | $a_{1}$ | $a_{2}$ | $a_{3}$ |
| $a_{1}$ | $b_{11}$ | $b_{12}$ | $b_{13}$ |
| $a_{2}$ | $b_{21}$ | $b_{22}$ | $b_{23}$ |
| $a_{3}$ | $b_{31}$ | $b_{32}$ | $b_{33}$ |
表 1中, bij表示对于指标ak而言ai与aj相比较的重要性, 一般由专家根据1~9标度法和指数标度法来确定。两种标度法分别如表 2和表 3所示。
表 2
1~9标度法
| 取值 | 定义 |
| 1 | 两元素相比, 重要性相同 |
| 3 | 两元素相比, 前者比后者稍重要 |
| 5 | 两元素相比, 前者比后者明显重要 |
| 7 | 两元素相比, 前者比后者极其重要 |
| 9 | 两元素相比, 前者比后者强烈重要 |
| 倒数 | 相反情况 |
表 3
指数标度法
| $1 \sim 9标度$ | 指数标度 |
| 1 | $9^{0}(1)$ |
| 3 | $9^{1 / 9}(1.277)$ |
| 5 | $9^{3 / 9}(2.080)$ |
| 7 | $9^{6 / 9}(4.327)$ |
| 9 | $9^{9 / 9}(9)$ |
1.1.3 权值确定及一致性检验
(1) 得出专家判断矩阵
| $\boldsymbol{A}=\left(a_{i j}\right)_{n \times n}$ | (1) |
(2) 对矩阵中各个元素进行按行乘积
| $ \prod\limits_{i=1}^{n} a_{i} $ | (2) |
(3) 对每行的向量作归一化处理
| $ \bar{W}_{i}=\sqrt[n]{\prod\limits_{i=1}^{n} a_{i}} $ | (3) |
(4) 计算权值
| $ W_{i}=\frac{\bar{W}_{i}}{\sum\limits_{i=1}^{n} \bar{W}_{i}} $ | (4) |
得到权重向量W=[W1, W2, W3, …, Wn]T。
(5) 一致性检验。判断矩阵只有通过一致性检验, 才能说明其在逻辑上的合理性, 才可以进一步分析结果。首先求出判断矩阵的最大特征值λmax, 再计算判断矩阵的一致性指标(Consistency Index, CI):
| $ C_{\mathrm{I}}=\frac{\lambda_{\max }-n}{n-1} $ | (5) |
CI值较大, 即表示判断矩阵的一致性较弱。因为实际中存在的一些随机因素, 往往使得一致性偏离, 所以一般依据CI与平均随机一致性指标(Random Consistency Index, RI)的比值CR来进行检验。
| $ C_{\mathrm{R}}=\frac{C_{\mathrm{I}}}{R_{\mathrm{I}}} $ | (6) |
其中RI的取值如表 4所示。
表 4
RI取值参考
| $n$ | $R_{\mathrm{I}}$ | $n$ | $R_{\mathrm{I}}$ |
| 1 | 0 | 6 | 1.24 |
| 2 | 0 | 7 | 1.32 |
| 3 | 0.58 | 8 | 1.41 |
| 4 | 0.90 | 9 | 1.45 |
| 5 | 1.12 |
依据经验, 当CR≤0.1时, 认为判断矩阵的一致性符合要求, 否则应重新构造判断矩阵, 再进行一致性检验, 直到满足要求。
1.2 粗糙集法确定指标客观权重
1.2.1 权重确定中RS的相关概念
一是决策表。表达特殊知识的系统即为决策表。其定义为:如果一个知识表达系统S=(U, A, V, f)中存在A=C∪D, 同时C∩D=∅, 则C和D分别称为对象的条件属性和决策属性, 此时S即为决策表。
二是不可辨识关系和上下近似集关系。在RS理论中, 一个知识库即表达一个关系系统, 记做K=(U, B), B是U上的一个等价关系, 用U/B来表示B的所有等价类构成的集合。基于以上理论将不可辨识关系定义为:若P⊆B, 并且P≠∅, 则P中所有等价关系的交集同样也是一个等价关系, 成为P上的不可辨识关系, 记做ind(P), 并且
| $ [x]_{\text {ind }(P)}={ }_{B \in P}^{I}[x]_{B} $ |
同样可得, 若K=(U, B)表示一个知识系统, 则ind(K)定义为K中的等价集合, 记作:
ind(K)={ind(K)|P⊆B, P≠∅}
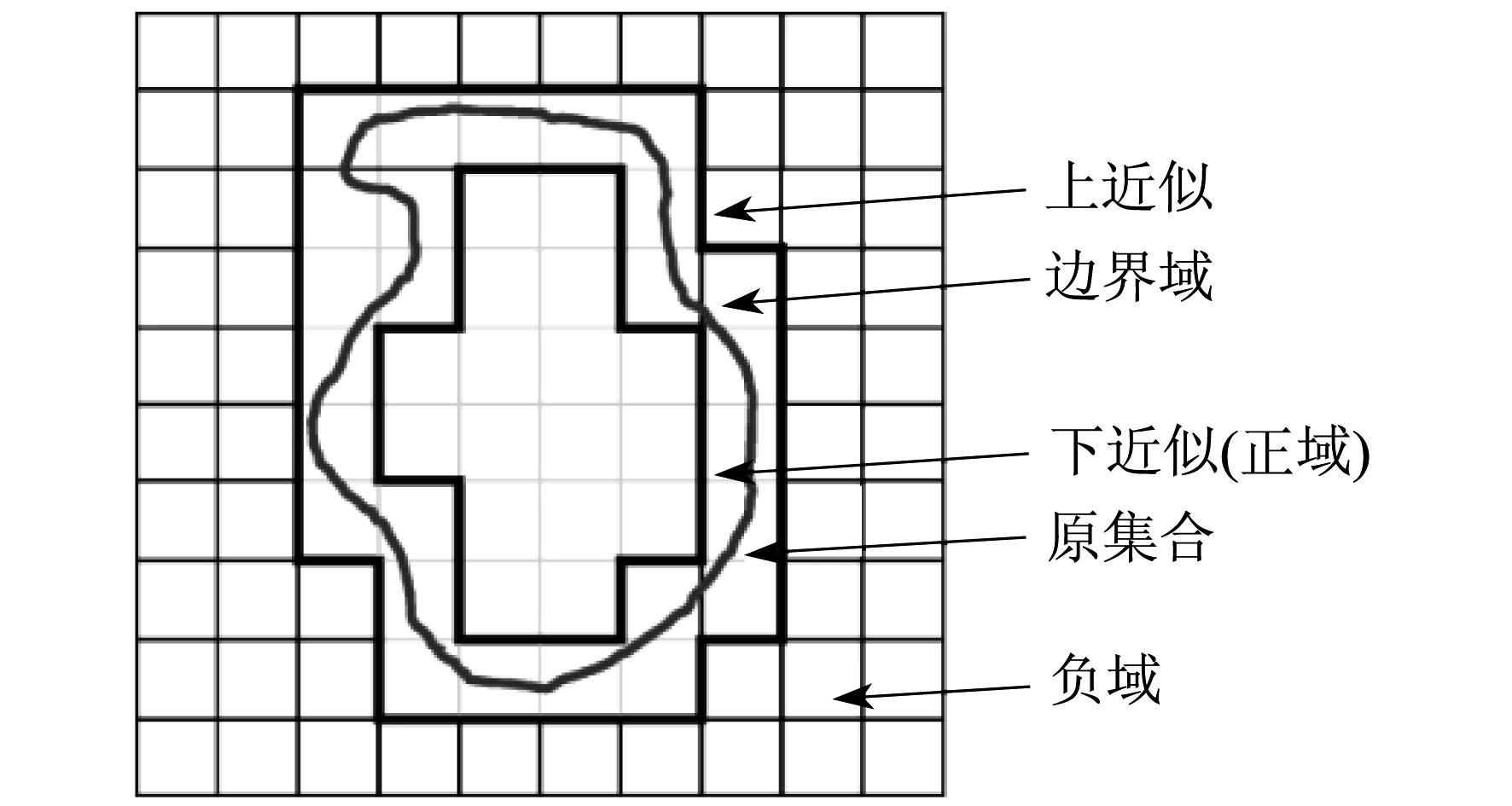
RS理论用上近似集和下近似集来表示一个粗糙集, 根据已有的分类知识得出其隶属函数, 因此元素与集合间隶属关系的不确定性可以得到较好的体现, 如图 1所示。
由图 1可知, 对一个确定的知识表达系统S=(U, A, V, f), 假设X为U上的一个任意非空子集, 有不可辨识关系ind(B), 则集合X的B上近似集和下近似集分别记为:
| $ \bar{B} X=\cup\left\{Y \in \frac{U}{\operatorname{ind}(B)} \mid X \cap Y \neq \varnothing\right\} $ |
| $ \underline{B X}=\cup\left\{Y \in \frac{U}{\mathrm{ind}(B)} \mid Y \subset X\right\} $ |
三是知识依赖度与属性重要性。用知识依赖度来表示属性知识对正域的依赖程度。若K=(U, B)表示一个知识库, 并且P⊆B, Q⊆B, 则Q对P的依赖度为
| $ \gamma_{P}(Q)=\frac{\operatorname{pos}_{p}(Q)}{U} $ | (7) |
对于属性的重要性, 若每一条属性ci⊆C, 则ci对决策属性D的重要性为
| $\sigma_{C D}\left(c_{i}\right)=\gamma_{C}(D)-\gamma_{C-c_{i}}(D)$ | (8) |
1.2.2 客观权重确定步骤
(1) 根据收集到的数据建立决策表, 离散各指标的数值, 去除重复信息。
(2) 按条件属性和决策属性各自进行分类, 并计算决策属性集D对条件属性集C及每一条件属性ci的依赖度。
(3) 计算步骤(2)中每一条件属性ci的重要性。
(4) 对得到的属性重要性作归一化处理, 从而得到各指标的权重。
1.3 基于AHP-RS的组合权重确定
在得到评价指标的主观权重和客观权重后, 为了避免使用客观权重可能偏离实际情况以及使用主观权重会增加主观因素干扰的情况, 参考已有研究成果, 利用最小相对信息熵原理将主客观权重进行组合[12-13]。
熵的概念来自热力学领域, 现代信息论创始人SHANNON C E将随机事件的不确定程度称为信息熵。此后, KULLBACK全面地阐述了随机不确定系统鉴别信息的概念, 被称为Kullback熵或相对熵[14], 其描述如下。
设随机变量X可能取值为an(n=1~N), 如果已知变量X在假设H1下的先验概率分布为P1(an), 则其过渡到假设H2下的概率分布P2(an)时所需的信息量即为随机变量X由假设H1向H2过渡所需的相对熵, 记为I(P2, P1)。
| $ I\left(P_{2}, P_{1}\right)=\sum\limits_{n=1}^{N} P_{2}\left(a_{n}\right) \ln \frac{P_{2}\left(a_{n}\right)}{P_{1}\left(a_{n}\right)} $ | (9) |
在最小相对熵原理中, 若在已知P1(an)的条件下, 要对P2(an)作出估计, 则必须满足从P1(an)过渡到P2(an)时所需相对熵最小的条件, 这说明在满足现有已知信息的前提条件下, 满足相对熵最小的后验概率P2(an)是最接近于P1(an)的概率分布, 其他所有概率分布函数都表明包含目前还未明确的已知信息[14]。
因此, 将其应用于评价指标权重的组合中, 令主观权重为W1(i), 客观权重为W2(i), 组合权重为W(i)。由最小相对信息熵原理有
| $ \begin{aligned} \min F=& \sum_{i=1}^{n} W(i)\left[\ln \frac{W(i)}{W_{1}(i)}\right]+\\ & \sum_{i=1}^{n} W(i)\left[\ln \frac{W(i)}{W_{2}(i)}\right] \end{aligned} $ | (10) |
式中,
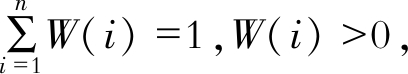 解得
解得
| $ W(i)=\frac{\left[W_{1}(i) W_{2}(i)\right]^{0.5}}{\sum\limits_{i=1}^{n}\left[W_{1}(i) W_{2}(i)\right]^{0.5}} $ | (11) |
由式(11)计算可得评价指标的组合权重。
2 实例分析
本文以某省级大型供电企业为例, 对其评价指标“职工安全培训状况”进行权重计算。
2.1 评价指标体系构建与评价等级划分
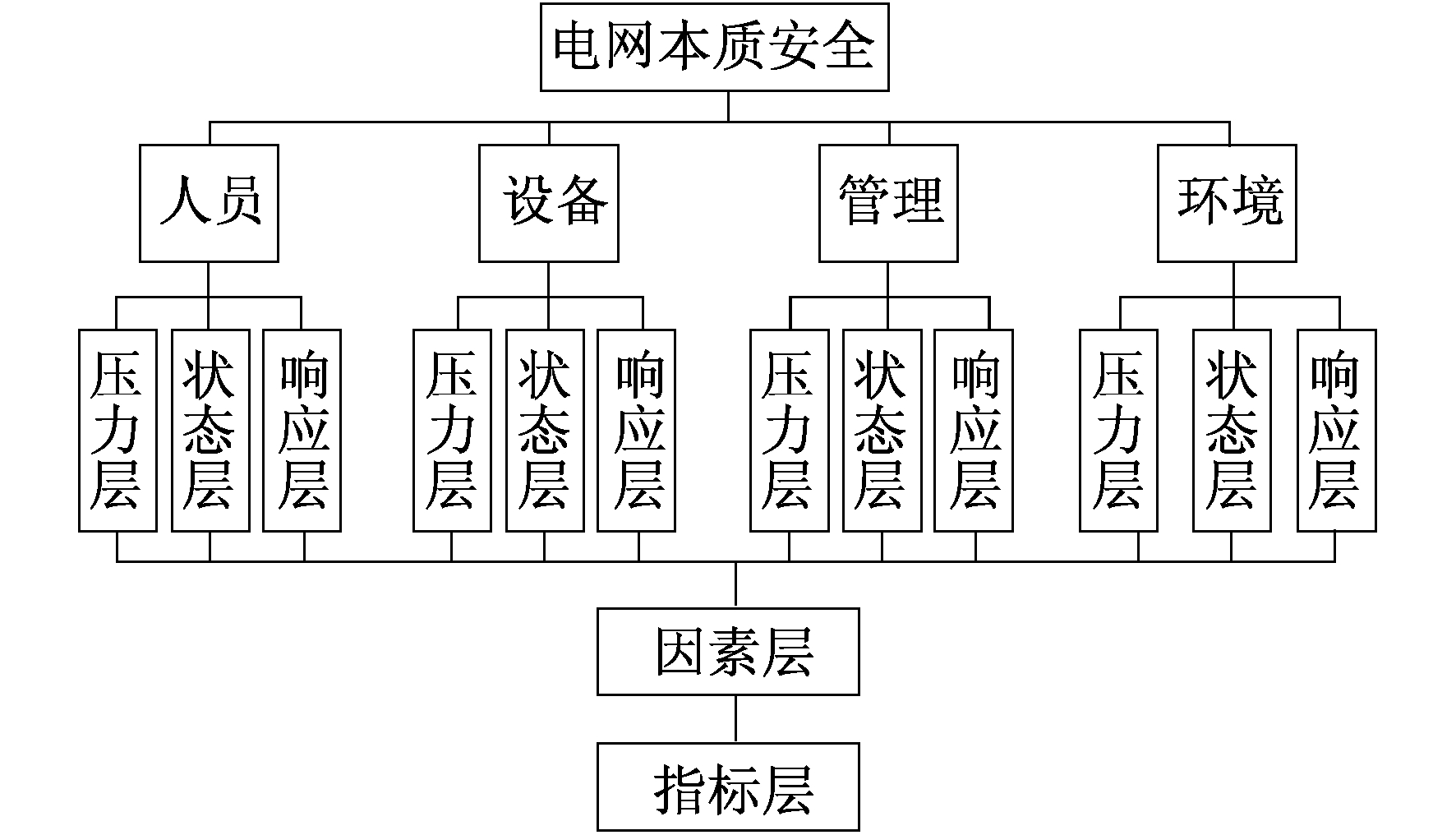
本文基于4M(人员-设备-管理-环境)-PSR(压力-状态-响应)的框架模型构建了5个层次的递阶结构式电网本质安全评价指标体系, 如图 2所示[15-16]。
第1层为评价总目标层, 又称总体层; 第2层为系统层, 包括人员、设备、管理、环境共4个子系统, 该层指标即为一级评价指标; 第3层为变量层, 每一个系统层的评价指标都由压力、状态、响应3层指标构成; 第4层为因素层, 该层指标组成了压力、状态、响应3层的评价因素, 称为二级评价指标; 第5层为指标层, 是整个评价指标体系中最具体、最基层的指标, 即为三级评价指标。
参考相关文献, 基于准确性和简便性的原则, 将电网本质安全评价等级划分为5个等级。将指标分值和评价分值都界定在[0, 1]内; 将评价分值分解为5个区间, 用模糊语言描述各个评价状态, 具体等级划分如表 5所示。
表 5
电网本质安全等级划分
| 本质安全等级 | 表征状态 | 评分 | 中位数 |
| 1(优秀) | 安全状态 | $0.85 \sim 1.00$ | 0.925 |
| 2(良好) | 较安全状态 | $0.70 \sim 0.85$ | 0.775 |
| 3(一般) | 预警状态 | $0.55 \sim 0.70$ | 0.625 |
| 4(较差) | 中警状态 | $0.40 \sim 0.55$ | 0.475 |
| 5(很差) | 重警状态 | $0.00 \sim 0.40$ | 0.200 |
2.2 评价指标权重计算
本文以二级评价指标职工安全培训状况A11为例进行计算。
2.2.1 客观权重计算
二级评价指标职工安全培训状况A11的三级评价指标分别为岗位培训A111, 日常培训A112, 特殊工种培训A113, 以A111, A112, A113作为条件属性, A11作为决策属性, 根据采集的数据构建了决策表, 如表 6所示。
表 6
初始决策表
| $U$ | $A_{111}$ | $A_{112}$ | $A_{113}$ | $D$ |
| 1 | 4 | 4 | 4 | 4 |
| 2 | 3 | 5 | 3 | 4 |
| 3 | 4 | 4 | 2 | 3 |
| 4 | 4 | 3 | 3 | 3 |
| 5 | 3 | 4 | 4 | 4 |
| 6 | 3 | 3 | 4 | 3 |
| 7 | 2 | 3 | 3 | 4 |
| 8 | 4 | 4 | 5 | 4 |
| 9 | 5 | 4 | 3 | 4 |
| 10 | 4 | 4 | 4 | 4 |
对表 6进行数据约简, 因10号数据与1号数据相同, 根据数据约简规则, 去掉10号数据, 得到简化的决策表如表 7所示。
表 7
最终决策表
| $U$ | $C$ | $D$ | ||
| $A_{111}$ | $A_{112}$ | $A_{113}$ | ||
| 1 | 4 | 4 | 4 | 4 |
| 2 | 3 | 5 | 3 | 4 |
| 3 | 4 | 4 | 2 | 3 |
| 4 | 4 | 3 | 3 | 3 |
| 5 | 3 | 4 | 4 | 4 |
| 6 | 3 | 3 | 4 | 3 |
| 7 | 2 | 3 | 3 | 4 |
| 8 | 4 | 4 | 5 | 4 |
| 9 | 5 | 4 | 3 | 4 |
对表 7的数据论域分别按条件属性和决策属性进行分类, 即
| $\frac{U}{\operatorname{ind}(D)}=\{\{1,2,5,8,9\},\{3,4,6,7\}\}$ |
| $\frac{U}{\operatorname{ind}(C)}=\{1,2,3,4,5,6,7,8,9\}$ |
分别去掉一个条件属性后的论域为
| $\frac{U}{\operatorname{ind}\left(C-A_{111}\right)}=\{\{1,5\}, 2,3,\{4,7\}, 6,8,9\}$ |
| $\frac{U}{\operatorname{ind}\left(C-A_{112}\right)}=\{1,2,3,4,\{5,6\}, 7,8,9\}$ |
| $\frac{U}{\operatorname{ind}\left(C-A_{113}\right)}=\{\{1,3,8\}, 2,4,5,6,7,9\}$ |
计算每一属性对于决策属性的重要性。
(1) 正域计算
| $\begin{aligned} P_{\mathrm{os}, C}(D) &=\{1,2,3,4,5,6,7,8,9\} \\ P_{\mathrm{os}, C-A_{111}}(D) &=\{1,2,3,4,5,6,7,8,9\} \\ P_{\mathrm{os}, C-A_{112}}(D) &=\{1,2,3,4,7,8,9\} \\ P_{\mathrm{os}, C-A_{113}}(D) &=\{2,4,5,6,7,9\} \end{aligned}$ |
(2) 重要性计算
| $ \begin{aligned} \gamma_{C}(D)=\frac{P_{\mathrm{os}, C}(D)}{U}=1 \\ \sigma_{D}\left(A_{111}\right)=\gamma_{C}(D)-\gamma_{C-A_{111}}(D)=1-\frac{9}{9}=0 \\ \sigma_{D}\left(A_{112}\right)=\gamma_{C}(D)-\gamma_{C-A_{112}}(D)=1-\frac{7}{9}=\frac{2}{9} \\ \sigma_{D}\left(A_{113}\right)=\gamma_{C}(D)-\gamma_{C-A_{113}}(D)=1-\frac{6}{9}=\frac{1}{3} \end{aligned} $ |
通过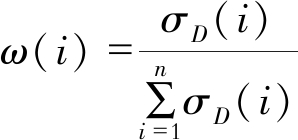 进行归一化处理, 得到所求各个三级指标的权重分别为0, 0.4, 0.6。
进行归一化处理, 得到所求各个三级指标的权重分别为0, 0.4, 0.6。
2.2.2 组合权重计算
主观权重的计算结果由AHP得出, 对A111, A112, A1133个评价指标采用1~9标度法构造判断矩阵, 详细步骤如1.1节所示, 3个评价指标主观权重的计算结果分别为0.244, 0.162, 0.594。为进一步校正主观权重与客观权重之间的偏差, 由式(11)将两个权重进行组合计算, 最终得到的组合权重结果为0, 0.299, 0.701。
为进一步表明本文计算得到的主观权重、客观权重以及组合权重对本次评价的影响程度, 绘制雷达图如图 3所示。
由图 3可知, 主观权重与客观权重在岗位培训A111、日常培训A112两个指标上的权重值差别较大, 说明单一赋权法存在缺点, 对数值的应用缺少说服力; 而组合权重几乎覆盖了主观权重和客观权重的整个重合区域, 能够较好地反映主观权重和客观权重的信息, 在一定程度上弥补了单一权重确定的不足, 使得权重确定结果更接近实际, 也更具有说服力。同时, 由图 3也可以看出, 特殊工种培训对评价的影响较大, 可在实际工作中加强该方面的管理和监督; 岗位培训的组合权重为零, 说明其相对重要程度较低, 对评价的影响较轻。
3 结语
赋权方法多种多样, 不同赋权法的结果差异较大, 以AHP为例的主观赋权法数据来源于专家经验, 不能保证赋权结果的客观性; 以RS法为例的客观赋权法完全依赖数据分析, 可能会造成赋权结果偏离实际的现象。针对这些不足, 本文提出利用最小相对信息熵原理将AHP和RS法分别确定的主观权重和客观权重进行组合, 并对由该方法得到的组合权重进行应用。结果表明, 该方法可行且合理, 能够提高评价结果的准确度。但在计算过程中未能避免部分主观数据的使用, 未能检验是否存在不合理的数据, 因此组合赋权法仍需作进一步的研究。
参考文献
-
[1]权重确定方法综述[J]. 农村经济与科技, 2018, 29(8): 252-253. DOI:10.3969/j.issn.1007-7103.2018.08.171
-
[2]多要素评价中指标权重的确定方法评述[J]. 知识管理论坛, 2017, 2(6): 500-510.
-
[3]基于AHP的分布式冷热电联产系统综合评价分析[J]. 上海电力学院学报, 2015, 31(5): 419-423.
-
[4]基于层次分析和模糊评价的电力信息系统风险评估方法[J]. 上海电力学院学报, 2013, 29(6): 518-522.
-
[5]赵晓琪. 4M-C-I视角下的煤矿本质安全评价研究[D].邯郸: 河北工程大学, 2017.
-
[6]张若思.电力企业本质安全的研究与实践[D].北京: 北京交通大学, 2012.
-
[7]张卫强.基于FNN模型的煤矿本质安全性评价及应用研究[D].西安: 西安科技大学, 2010.
-
[8]基于粗糙集-理想点法的岩爆预测[J]. 浙江大学学报, 2014, 48(3): 498-503.
-
[9]基于粗糙集的高铁客运站服务质量评价模型[J]. 交通运输系统工程与信息, 2014, 14(2): 132-137. DOI:10.3969/j.issn.1009-6744.2014.02.021
-
[10]粗糙集理论在情报分析指标权重确定中的应用[J]. 实践研究, 2012, 35(9): 61-65.
-
[11]孟钰莹.基于粗糙集和云模型的专利价值综合评价[D].北京: 首都经济贸易大学, 2018.
-
[12]基于ANP和VPRS的高速列车舒适性综合评价指标权重分析[J]. 铁道学报, 2014, 36(6): 15-20. DOI:10.3969/j.issn.1001-8360.2014.06.003
-
[13]基于熵组合权重-AHP的杭州市下沙海堤社会影响评价[J]. 中国水运(下半月), 2011, 11(4): 48-49.
-
[14]基于最小相对熵原理的区域投入产出直接消耗系数修订模型[J]. 华北水利水电大学学报(自然科学版), 2016, 37(5): 40-45.
-
[15]基于PSR模型的煤矿本质安全评价新方法[J]. 煤炭技术, 2014, 33(9): 42-44.
-
[16]徐磊.基于PSR模型的煤矿本质安全性评价方法与应用研究[D].西安: 西安科技大学, 2009.