|
|
|
发布时间: 2019-10-10 |
|
|
|
|
收稿日期: 2019-04-02
中图法分类号: TP27
文献标识码: A
文章编号: 1006-4729(2019)05-0455-04
|
摘要
通过对小型光电编码器输出的光电信号精度误差来源进行研究, 得出了正交性偏差是其主要误差来源的结论。针对光电编码器输出信号正交性误差的测量, 引入了一种改进的坐标旋转数字计算机算法。该算法是在传统坐标旋转数字计算算法的基础上, 通过改进其迭代结构得到的, 能够很好地实现对光电编码器输出信号的正交性误差进行动态实时测量。MATLAB软件仿真结果显示, 与其他方法相比, 利用该方法测量的正交性误差范围明显更小、检测精度更高且运算速率更快。
关键词
正交性误差; 坐标旋转数字计算机算法; 光电编码器; 精度细分误差; 莫尔条纹
Abstract
Through the study of the error source of the photoelectric signal output of the small photoelectric encoder, it is concluded that the orthogonal deviation is the main source of error.Then, aiming at the measurement of the orthogonality error of its output signal, an improved coordinate rotation digital calculation method is introduced, which is an algorithm based on the traditional coordinate rotation digital calculation method by improving its iterative structure.The algorithm can well realize real-time kinematic survey of the orthogonality of the signal output to the photoelectric encoder.The simulation results with MATLAB software show that compared with other methods, the orthogonality error is measured by this method with a smaller range, higher accuracy and higher computing speed.
Key words
orthogonality error; coordinate rotation digital computer algorithm; photoelectric encoder; precision subdivision error; moire fringe
随着工业控制技术的不断进步与快速发展, 该行业对光电编码器精度的要求也不断提高。对光电编码器进行深入研究不难发现, 其最主要的测量误差来源是细分精度误差, 而光电编码器输出信号的质量也对其细分精度产生较大的影响[1-2]。在理想状态下, 光电编码器的输出信号是两个相位差为π/2的标准正弦波形信号, 然而实际采集到的光电编码器莫尔条纹光电信号受到码盘刻画工艺、系统噪声、器件安装工艺等各种因素的影响, 会导致实际信号中含有多项误差, 严重影响了编码器的细分精度。实际的两路莫尔条纹信号由于一些因素的影响而存在直流电平漂移、高次谐波等信号误差[3-4]。
在各项指标中, 光栅莫尔条纹信号的正交性误差是衡量其测量精度的一项重要指标。因此, 开展对光电编码器输出信号的正交性误差测量研究是提高其精度测量的一个重要环节。目前, 美国天文台提出了基于Heidenhain模型的补偿方法, 但是该方法计算量大; 罗刚等人[5]采用了一种基于锁相环的检测方法, 但该方法存在“高频失锁”现象。本文在前人研究的基础上引入了一种基于改进型的坐标旋转数字计算机(Coordinate Rotation Digital Computer, CORDIC)算法来实时检测光电编码器的正交性误差。该方法很少被运用到编码器正交性偏差的实时检测领域。
1 CORDIC算法
1.1 CORDIC算法的基本原理
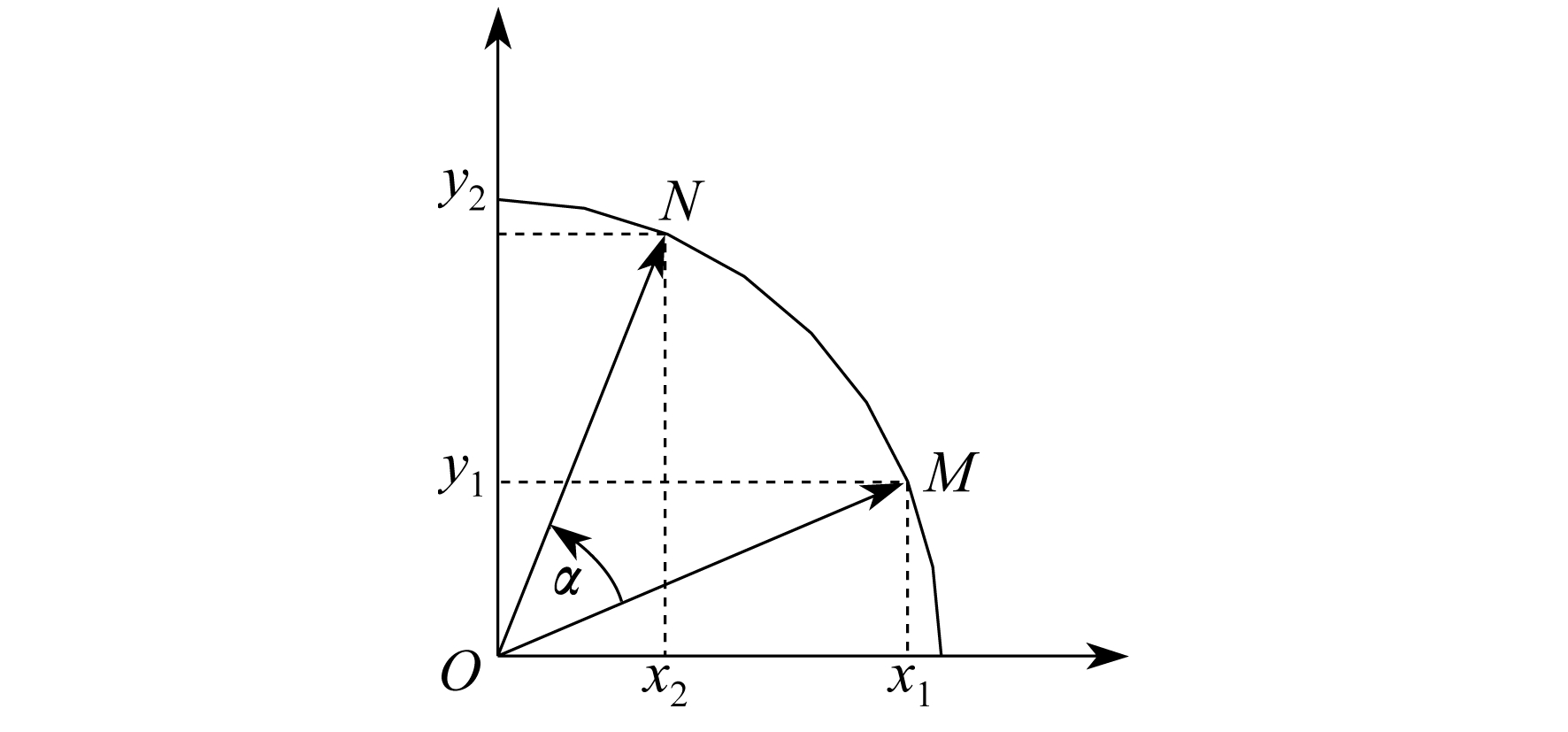
在笛卡尔坐标系中, 向量旋转示意图如图 1所示。
将平面上的矢量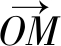 以原点为中心逆时针旋转α角度, 得到矢量
以原点为中心逆时针旋转α角度, 得到矢量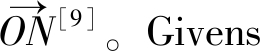 旋转的标准表示方法如下
旋转的标准表示方法如下
| $ \begin{aligned} \left[\begin{array}{l} x_{2} \\ y_{2} \end{array}\right]=& \left[\begin{array}{cc} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right]\left[\begin{array}{l} x_{1} \\ y_{1} \end{array}\right]=\\ \cos \alpha\left[\begin{array}{rr} 1 & -\tan \alpha \\ \tan \alpha & 1 \end{array}\right]\left[\begin{array}{l} x_{1} \\ y_{1} \end{array}\right] \end{aligned} $ | (1) |
假设经过n次旋转之后才从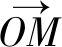 矢量旋转到
矢量旋转到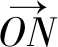 矢量, 则此过程总的表达式为
矢量, 则此过程总的表达式为
| $\left[\begin{array}{l}x_{2} \\ y_{2}\end{array}\right]=k_{n}\left[\begin{array}{cc}1 & -\tan \delta_{n-1} \alpha_{n-1} \\ \tan \delta_{n-1} \alpha_{n-1} & 1\end{array}\right] \cdots \\ \left[\begin{array}{cc}1 & -\tan \delta_{0} \alpha_{0} \\ \tan \delta_{0} \alpha_{0} & 1\end{array}\right]\left[\begin{array}{l}x_{1} \\ y_{1}\end{array}\right]$ | (2) |
式中:kn——校模因子, 其取值的大小只与迭代次数n有关;
δi——判断因子, 主要是用来表示旋转方向的一个参数, δi∈{-1, 1}, 当δi=1则表示下一次的旋转方向为逆时针, 当δi=-1则表示下一次的旋转方向为顺时针。
当n足够大时, 校模因子kn可以表示为
| $ \begin{aligned} & k_{n}=\prod_{i=0}^{n-1} \cos \alpha_{i}=\prod_{i=0}^{n-1} \frac{1}{\sqrt{1+2^{-2 i}}} \approx\\ & 0.607253 \end{aligned} $ | (3) |
传统CORDIC算法在笛卡尔坐标系下的基本迭代关系公式为
| $ \left\{\begin{array}{l} x_{i+1}=x_{i}-\delta_{i}\left(2^{-i} y_{i}\right) \\ y_{i+1}=y_{i}-\delta_{i}\left(2^{-i} x_{i}\right) \\ z_{i+1}=z_{i}-\delta_{i} \arctan 2^{-i} \end{array}\right. $ | (4) |
式中:i——旋转次数。
该算法的收敛域约为[-99.88°, 99.88°]。CORDIC算法存在有两种不同的工作模式:旋转模式(Vectoring Mode, VM)和向量(Rotation Mode, RM)模式。根据判断因子δi取值的正负, 来表征传统CORDIC算法的工作方式是处于向量模式下还是处于旋转模式下。
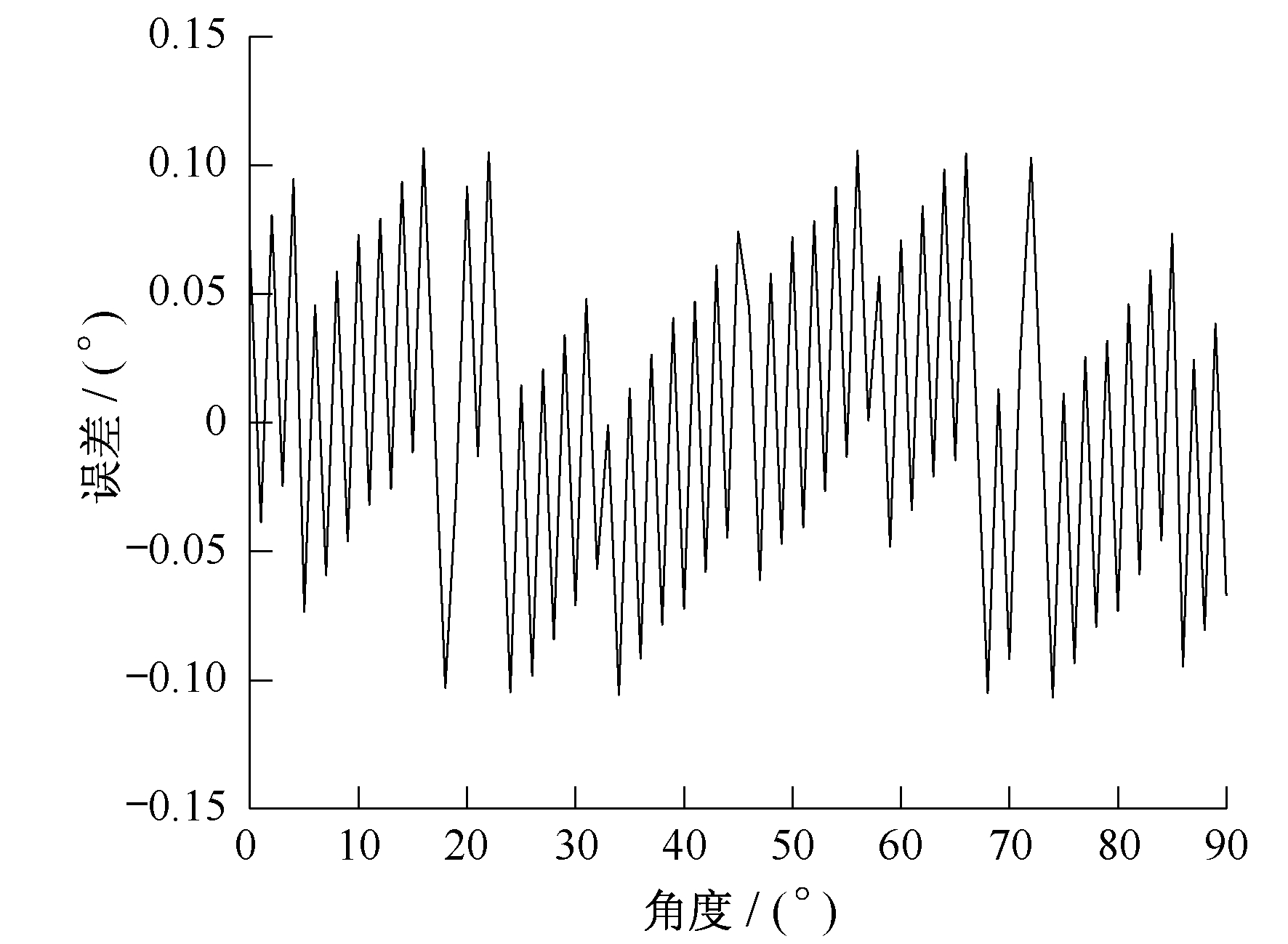
1.2 传统的CORDIC算法的误差
2 改进的CORIDC算法
常规的CORDIC算法迭代在角度计算时, 会引入乘法和平方根运算, 增加运算量, 因此本文引入双迭代法(Double Iteration Algorithm)。其原理是进行两次基本角度的迭代旋转, 主要优势在于将随着向量旋转而变化的参数由乘法平方根变为加法和移位运算, 公式如下
| $ \left\{\begin{array}{l} x_{0}=1, y_{0}=0, z_{0}=0 \\ {\left[\begin{array}{l} x_{i+1} \\ y_{i+1} \end{array}\right]=\left[\begin{array}{cc} 1 & -\delta_{i} 2^{-i} \\ \delta_{i} 2^{-i} & 1 \end{array}\right]^{2}\left[\begin{array}{l} x_{i} \\ y_{i} \end{array}\right]} \\ z_{i+1}=z_{i}+2 d_{i} \arctan 2^{-i} \end{array}\right. $ | (5) |
由于改进的CORDIC算法的迭代次数发生变化, 改变了kn的大小, 所以改进的CORDIC算法的增益因子为
| $ k_{n}^{\prime}=k_{n} \prod\limits_{i=0}^{n} \cos \alpha_{i} $ | (6) |
本文通过对迭代过程进行观察发现, 当输入的数据参数接近1时, 向量可能会旋转至第二象限, 此时x的值变为负值, 得出的角度也会大于90°。在任何一级迭代过程中, 只要向量旋转至第二象限, 则在下一级迭代过程中必须旋转至第一象限。因此, 需要增加一个条件, 即
| $ \delta_{i}=\left\{\begin{array}{ll} -1 & x_{i} \leqslant 0 \\ +1 & x_{i} \gt 0 \end{array}\right. $ | (7) |
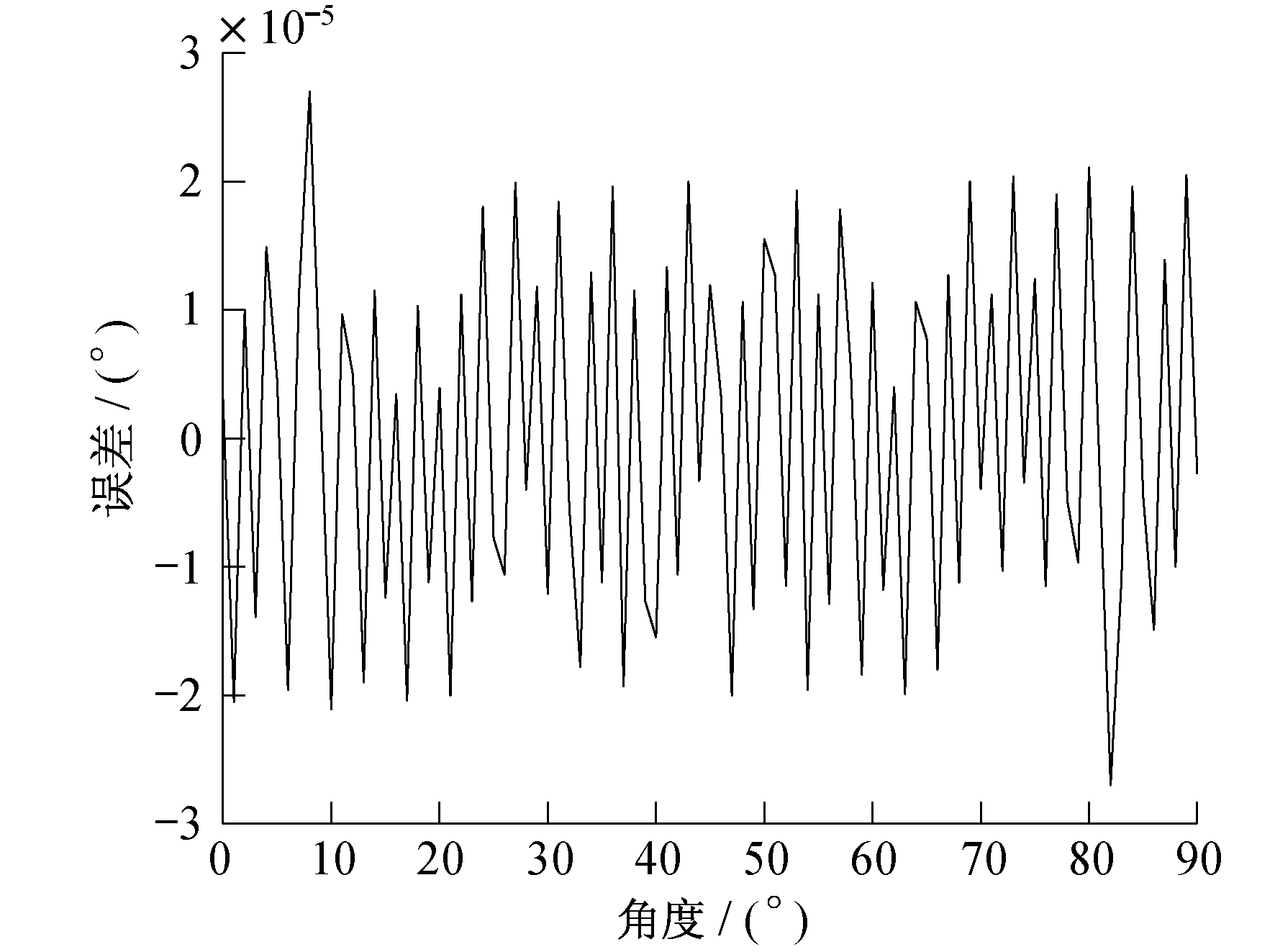
在仿真软件MATLAB环境下, 利用该算法对[0°, 90°]范围内的余弦角度进行解算, 其解算误差如图 3所示。
对比图 2和图 3可以发现, 改进的CORDIC算法误差明显减小, 在[0°, 90°]范围内的最大解算误差仅为3×10-5°。由此可知, 基于改进的CORDIC算法可以更有效地实现对角度的计算。
3 正交性误差仿真检测
在MATLAB仿真环境下, 模拟产生两路正弦的信号, 并设置其在[0°, 10°]范围内产生不同的相位差, 再利用改进的CORDIC算法对这两路正弦信号的相位差进行检测, 最后得出信号的相位差测量误差。其仿真结果如图 4所示。
由图 4可知, 利用相位差计算算法的误差范围在[-0.03°, 0.03°], 误差最大值为0.027°, 最小值为0.004°。将本文中提出的改进的CORDIC算法与相关函数法、傅里叶变换法的测量误差在相同的条件下进行比较[10], 取光电莫尔条纹的100个采样点进行测量, 实际的正交性误差在[0°, 10°]范围内, 对两路正弦信号的正交性误差进行测量, 测量误差范围如表 1所示。
表 1
不同方法下正交性误差测量误差范围
| 测量方法 | 测量误差范围 |
| 傅里叶变换法 | $\left[-0.2^{\circ}, 0.2^{\circ}\right]$ |
| 相关函数法 | $\left[-0.1^{\circ}, 0.1^{\circ}\right]$ |
| 改进的CORDIC算法 | $\left[-0.03^{\circ}, 0.03^{\circ}\right]$ |
实验结果表明, 在相同条件下, 改进的CORDIC算法与其他测量方法相比, 正交性测量误差范围更小, 精度更高。
由此可见, 本文提出的正交性误差测量方法能够有效地保证光电莫尔条纹信号的测量精度, 实现对光电编码器输出信号的正交性误差进行动态实时测量。
4 结语
本文对光电编码器输出信号的正交性误差进行了研究, 在传统的CORDIC算法基础上进行了改进, 改进优化后的CORDIC算法在角度解算上的误差明显减小, 提高了检测准确度。在MATLAB仿真环境下利用改进的CORDIC算法检测正弦仿真信号的相位差, 并在相同条件下将此算法的测量误差与其他的检测方法进行比较, 结果显示, 改进的CORDIC算法对输出信号的正交性误差测量的误差范围更小, 对光电编码器的自动校准系统具有现实应用意义。
参考文献
-
[1]光电轴角编码器光电信号正交性偏差的相量校正方法[J]. 光学精密工程, 2007, 15(11): 1745-1748. DOI:10.3321/j.issn:1004-924x.2007.11.018
-
[2]郭瑞.增量式光电编码器莫尔条纹信号细分方法研究[D].南京: 南京航空航天大学, 2013.
-
[3]光纤布拉格光栅应力传感技术研究与应用[J]. 上海电力学院学报, 2017, 33(1): 25-29.
-
[4]光电轴角编码器细分信号误差及精度分析[J]. 光学精密工程, 2012, 20(2): 379-386.
-
[5]光电轴角编码器光电信号正交偏差的测量和补偿方法[J]. 传感技术学报, 2008, 21(11): 1853-1857. DOI:10.3969/j.issn.1004-1699.2008.11.009
-
[6]CORDIC算法的优化及实现[J]. 北京理工大学学报, 2015, 35(11): 1164-1170.
-
[7]多模式CORDIC算法结构改进与实现[J]. 电子学报, 2018, 46(2): 495-500. DOI:10.3969/j.issn.0372-2112.2018.02.032
-
[8]一种基于FPGA的CORDIC算法的实现[J]. 电子测量技术, 2018, 41(5): 47-50.
-
[9]基于CORDIC算法的正交信号源实现[J]. 现代电子技术, 2016, 39(7): 57-59.
-
[10]莫尔条纹光电信号正交性偏差的实时补偿[J]. 光学精密工程, 2014, 22(1): 213-219.