|
|
|
发布时间: 2019-10-10 |
|
|
|
|
收稿日期: 2019-05-15
基金项目: 上海市电站自动化技术重点实验室(13DZ2273800)
中图法分类号: TP29
文献标识码: A
文章编号: 1006-4729(2019)05-0465-07
|
摘要
针对电厂协调控制系统, 提出了一种基于支持向量机(SVM)的广义预测控制(GPC)建模方法和控制算法。首先, 根据电厂机组的实际运行参数, 建立了600 MW亚临界燃煤机组协调控制系统受控对象的数学模型。其次, 在建模过程中提出了一种新的混合优化算法——差分进化-灰狼优化混合算法(DE-GWO), 以优化SVM, 提高模型的准确性。最后, 将基于SVM的GPC算法用于电站协调控制系统的设计。仿真结果表明, 所提方法具有良好的跟踪能力和较强的鲁棒性。
关键词
广义预测控制; 混合优化算法; 支持向量机
Abstract
Aiming at the coordinated control system of power plants, a modeling method and control algorithms based on support vector machine (SVM) for generalized predictive control (GPC) is proposed.Firstly, according to the actual operation parameters of a power plant unit, the mathematical model of the controlled object of a 600 MW subcritical coal-fired unit coordinated control system is established.Secondly, a new hybrid optimization algorithm, namely, DE-GWO, is proposed to optimize SVM in order to improve the accuracy of the model.Finally, the coordinated control system is designed by using the generalized predictive control algorithm based on SVM.The simulation results show that the proposed method has good tracking ability and strong robustness.
Key words
generalized predictive control; hybrid optimization algorithm; support vector machine
火电单元机组的协调控制系统(Coordinated Control System, CCS)是20世纪80年代引入中国的火电站控制理念, 在实现对锅炉主蒸汽压力和机组负荷控制的同时, 协调锅炉空气、燃料和给水的响应。CCS的被控对象, 即单元机组(Boiler-Turbine Unit, BTU)具有多输入、多输出、非线性、强耦合等特性, 面对这样复杂的系统, 机理建模方法难以建立准确的数学模型。
在火力发电厂中广泛应用的工厂级监控信息系统(Supervirsory Information System, SIS)和分散控制系统(Distributed Control System, DCS), 使得现场实时数据和以前的运行历史数据的获取更加便捷, 因此可以利用“黑箱建模”数据驱动方法, 也就是基于输入输出数据的方法, 来建立单元机组协调控制系统被控对象的数学模型, 其中较为典型的建模方法, 如基于神经网络与支持向量机(Support Vector Machine, SVM)的识别和建模[1-3]。文献[1]将神经网络和遗传算法相结合, 利用电厂数据训练神经网络, 以便及时预测燃料输入量, 并将其应用于某600 MW火电厂被控对象的建模。文献[2]采用神经网络算法与预测控制相结合的方法, 利用BP神经网络的非线性拟合特性来识别协调控制系统的受控对象, 从而建立了动态模型。但神经网络有其本质的缺陷, 缺乏严谨的理论依据作支撑[4], 而SVM则有严谨的理论依据, 且具有快速训练的速度和全局解的优势, 并兼备了优异的拟合非线性函数能力, 在系统辨识和建模领域得到了应用[5]。在建模的过程中, 为了寻求最优的惩罚因子与核函数参数以提高SVM建模的准确度, 考虑结合差分进化(Differential Evolution, DE)算法与灰狼优化(Grey Wolf Optimizer, GWO)算法各自的优点[6], 通过采用一种全新的混合优化算法——差分进化-灰狼优化(DE-GWO)混合算法来优化SVM, 则可以避免早熟停滞, 同时可以提高全局搜索能力, 从而提高SVM建模的准确性。
预测控制是基于模型的先进控制算法。而基于线性受控自回归积分滑动平均(Controlled Auto-Regressive Integrated Moving Average, CARIMA)模型的广义预测控制(Generalized Predictive Control, GPC)算法, 对模型的要求低, 鲁棒性好, 抑制干扰能力强, 属于可在计算机上实现的智能控制算法, 具有较强的优势[7-8]。如果将SVM建模方法与GPC相结合, 采用基于混合算法优化的SVM来建立预测模型, 就可以将基于SVM的GPC算法应用于单元机组协调控制系统的设计中。
1 基于支持向量机的广义预测控制
GPC算法利用最小方差控制中的CARIMA模型来表示控制对象[9]
| $ \begin{aligned} A\left(z^{-1}\right) y(k)=& B\left(z^{-1}\right) u(k-1)+\\ & \frac{C\left(z^{-1}\right) \cdot \xi(k)}{\Delta} \end{aligned} $ | (1) |
其中
| $ \left\{\begin{array}{l} A\left(z^{-1}\right)=1+\sum\limits_{i=1}^{n_{a}} a_{i} \cdot z^{i} \\ B\left(z^{-1}\right)=b_{0}+\sum\limits_{i=1}^{n_{b}} b_{i} \cdot z^{i} \\ C\left(z^{-1}\right)=C_{0}+\sum\limits_{i=1}^{n_{c}} c_{i} \cdot z^{i} \end{array}\right. $ | (2) |
式中:z-1——后移算子, 表示后退一个采样周期的相应的量;
na, nb, nc——分别对应a, b, c的下标最大序号;
C(z-1)ξ(k)/Δ——系统的噪声项, 为方便推导, 这里假设C(z-1)=1;
ξ(k)——不相关的随机噪声序列;
Δ——差分算子, Δ=1-z-1;
A, B, C——关于z-1的多阶表达式。
其中, 式B(z-1)中为零的元素b0, b1, b2…表示对象的滞后时间。为了便于分析, 将噪声项忽略不计, 将式(1)转换成没有后移算子z-1的表达式, 即
| $ \begin{array}{l} y(k)+a_{1} y(k-1)+\cdots+a_{n_{a}} y\left(k-n_{a}\right)= \\ b_{0} u(k-1)+b_{1} u(k-2)+\cdots+ \\ b_{n_{b}} u\left(k-n_{b}-1\right) \end{array} $ | (3) |
整理后可得的差分方程为
| $ \begin{aligned} y(k)=& -a_{1} y(k-1)-a_{n_{a}} y\left(k-n_{a}\right)+\\ & b_{0} u(k-1)+b_{1} u(k-2)+\cdots+\\ & b_{n_{b}} u\left(k-n_{b}-1\right) \end{aligned} $ | (4) |
由式(4)可知, SVM表达式与差分方程结构相似, 其结构形式为
| $y(k)=f\left(V_{k}\right)=f[y(k-1), \cdots, y(k-n+1)$ $u(k-1), \cdots, u(k-m+1)]$ | (5) |
式(5)中f(·)是具有SVM结构的函数, 而
| $\begin{aligned} V_{k} &=[y(k-1), \cdots, y(k-n+1)\\ &u(k-1), \cdots, u(k-m+1)] \end{aligned}$ | (6) |
为SVM形式。
考虑式(5)中SVM的结构形式, 选择线性核函数
| $K\left(x, x_{i}\right)=x \cdot x_{i}$ | (7) |
凭借SVM的训练与学习, 可得到对应的支持向量和它们的阈值b与系数ai(i=1, 2, 3, …, N)。故有
| $ y(k)=\sum\limits_{i=1}^{N} a_{i}\left(V_{i}^{\prime} \cdot V_{k}\right)+b $ | (8) |
式中:{V′i}(i=1, 2, 3, …, N)——支持向量集合。
由于选择了线性核函数, 故可以将内积V′i·Vk展开。展开后的表达式为
| $\begin{aligned} V_{i}^{\prime} \cdot V_{k}=& V_{i}^{\prime}(1) y(k-1)+\\ & V_{i}^{\prime}(2) y(k-2)+\cdots+\\ & V_{i}^{\prime}(n-1) y(k-n+1)+\\ & V_{i}^{\prime}(n) u(k-1)+\cdots+\\ & V_{i}^{\prime}(n+m) u(k-1+m) \end{aligned}$ | (9) |
令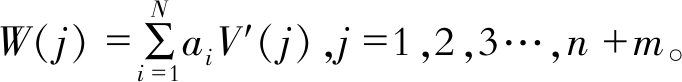 因此基于线性核函数的前向SVM结构可表示为
因此基于线性核函数的前向SVM结构可表示为
| $\begin{aligned} y(k)=& W(1) y(k-1)+\cdots+\\ & W(n-1) y(k-n+1)+\\ & W(n) u(k-1)+\cdots+\\ & W(n+m) u(k-m+1) \end{aligned}$ | (10) |
将式(10)与式(4)比较可得a1, a2, a3, …, ana, b0, b1, b2, …, bnb的系数。
需要指出的是, 本文在利用SVM进行系统建模时, 核函数一般选择易于展开内积的线性核函数, 且不需要明确系统的时间滞后参数, 可根据经验估计大致滞后时间范围, 以此构建训练样本, 最后由辨识结果可知系统明确的滞后时间。假设辨识出b0, b1, b2, b3, b4是零, 那么可知系统滞后5个采样周期。这种方法优于最小二乘法。一方面最小二乘法不能像上述方法一样辨识出系统的滞后时间, 另一方面上述方法对数据的数量、质量要求较低。因此, 基于线性核函数的SVM建模方法可以较好地解决建模中遇到的问题[10]。
2 混合优化算法
在建模过程中, SVM惩罚参数与核函数参数对建模准确度的影响较大, 应考虑采用智能算法来寻找最佳的SVM参数[11]。对于DE算法和GWO算法, 它们在各自优化过程中存在易陷入局部最优和早熟等问题。通过结合各自的优点, 提出具有优异全局搜索能力的混合优化算法——DE-GWO。以此为基础, 采用SVM来构建预测模型。
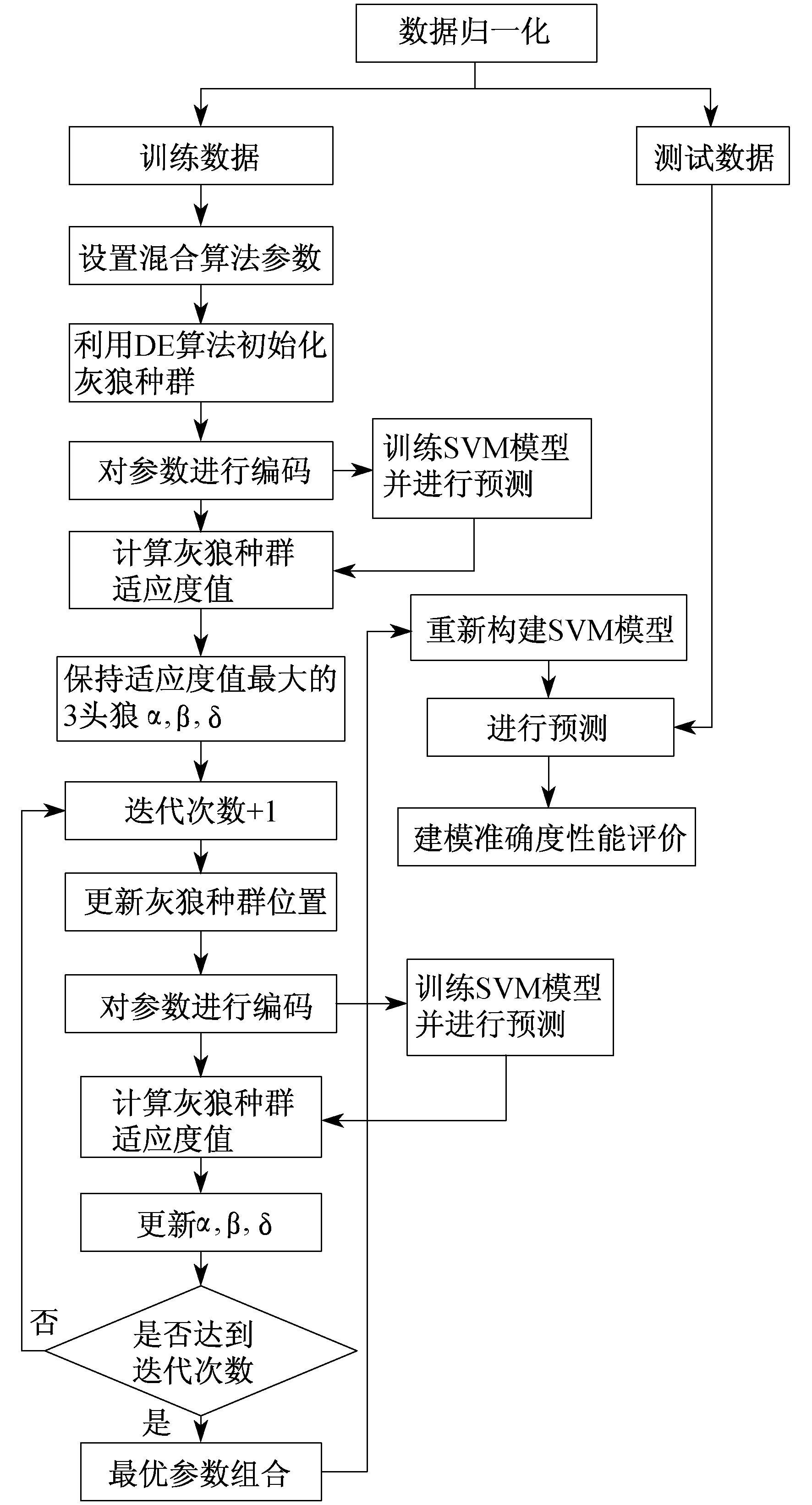
首先, 利用DE算法的差分种群生成初始种群, 保持灰狼算法初始种群的差异性和多样性。然后根据计算所得个体目标函数值, 选择最优的3个灰狼α, β, δ, 对其他灰狼位置进行更新, 引入灰狼算法与差分进化算法的交叉、选择算子进行全局搜索, 利用灰狼算法全局最优解搜索能力以确保算法的收敛, 更新灰狼个体位置, 直至输出最佳迭代目标值。此混合算法提高了算法的全局搜索能力, 有效解决了陷入局部最优与早熟停滞等问题, 从而寻找到最佳的SVM参数, 提高了建模的准确性。
基于DE-GWO的SVM所建预测模型算法流程如图 1所示。
3 基于混合算法SVM建立机组负荷-压力预测模型
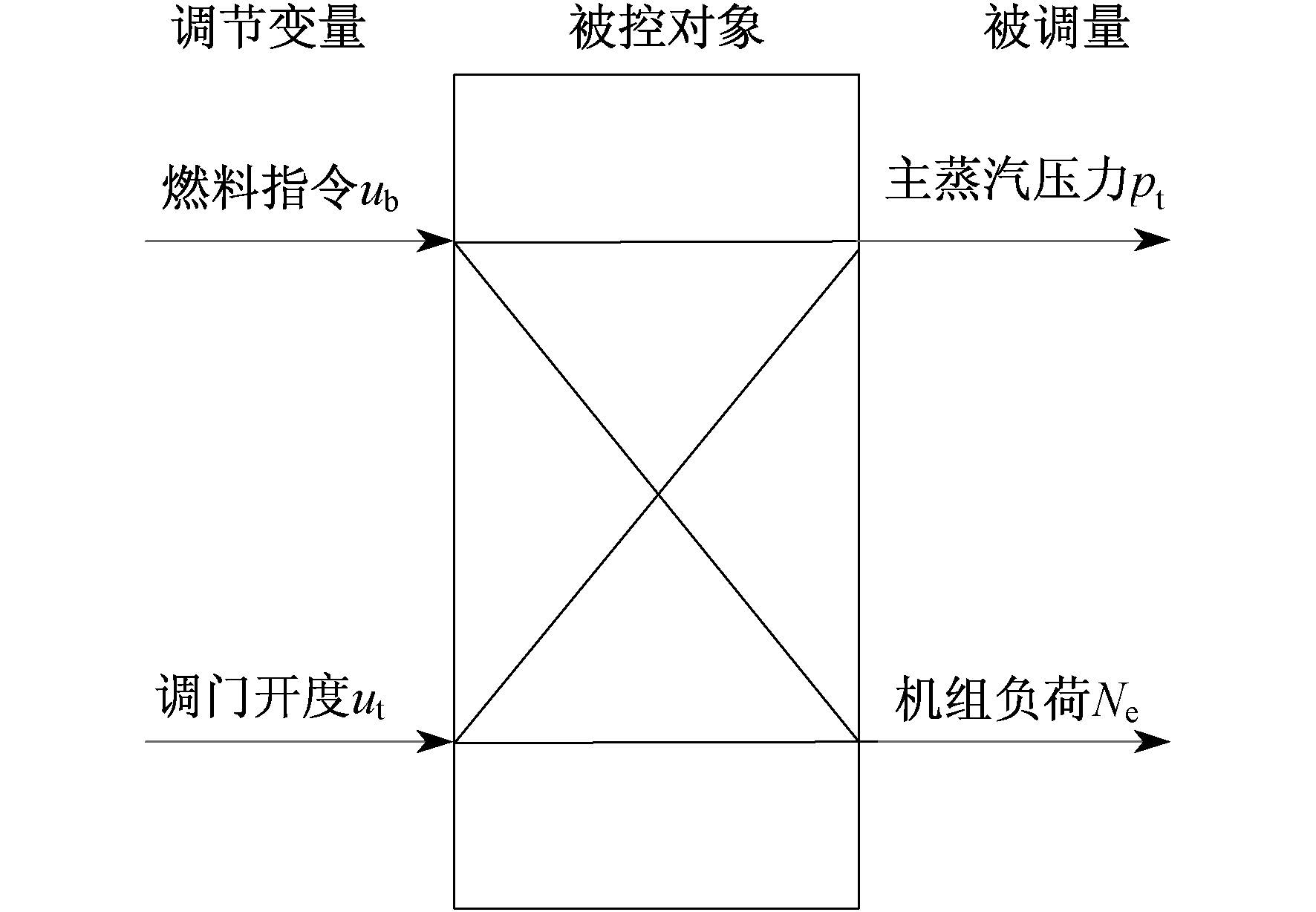
单元机组是一个相互耦合的两输入两输出被控对象。两个输入量分别为汽轮机调门开度ut和燃烧指令ub (给煤量), 两个输出量分别为机前压力pt (主蒸汽压力)和机组负荷Ne。CCS的主要任务, 一是保证机组快速跟踪负荷的变化, 二是要维持机前压力的基本稳定, 以确保机组的安全经济运行[12]。亚临界机组协调控制系统对象结构如图 2所示。
采用某电厂3#机组为被控对象。锅炉为亚临界一次中间再热汽包锅炉, 型号为HG-2023/17.6-YM4;汽轮机为单轴四缸四排汽凝汽式汽轮机, 型号为N600-16.7/537/537-I。正常情况下, 机组运行方式采用滑压式, 50%~100%工况范围内可以不投油助燃。
用来建模的数据来自该电厂SIS数据库, 包括燃料指令、汽轮机调门开度数据各1 300组, 机前压力(主蒸汽压力)和机组负荷数据各1 300组, 随机取1 000组数据用来建模, 建立100%工况点处对象模型。部分数据如表 1所示。
表 1
输入输出部分原始数据
| 给煤量/(t·h-1) | 调门开度/(%) | 主蒸汽压力/MPa | 机组负荷/MW |
| 180.4658203 | 56.172 | 16.122 | 415.1871304 |
| 180.7898712 | 56.429 | 16.128 | 415.3257713 |
| 180.8720971 | 56.987 | 16.139 | 415.4607508 |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ |
| 261.0874634 | 69.433 | 16.817 | 607.3203421 |
| 261.0359803 | 69.701 | 16.823 | 607.3967602 |
| 261.0539856 | 69.832 | 16.834 | 607.5136069 |
利用表 1所述输入输出数据, 采用基于混合算法优化的SVM建立该电厂单元机组协调控制系统预测模型, 预测模型的预测输出如表 2所示。为了比较改进后混合算法优化的SVM所建预测模型的准确性, 通过对比改进前基于SVM所建预测模型的预测输出, 衡量两组预测输出与原始输出数据的拟合度, 来评价拟建预测模型的准确性。
表 2
预测模型输出数据
| 基于SVM主蒸汽压力预测输出/MPa | 基于SVM机组负荷预测输出/MW | 混合算法优化SVM主蒸汽压力预测输出/MPa | 混合算法优化SVM机组负荷输出/MW |
| 16.109 | 407.956 178 6 | 16.134 | 413.227 591 4 |
| 16.116 | 409.376 375 3 | 16.141 | 412.935 901 3 |
| 16.125 | 409.637 931 2 | 16.147 | 413.463 092 8 |
| ⋮ | ⋮ | ⋮ | ⋮ |
| 16.791 | 618.736 777 8 | 16.783 | 613.165 389 2 |
| 16.795 | 617.973 713 1 | 16.788 | 612.883 640 1 |
| 16.801 | 618.438 670 9 | 16.803 | 613.369 721 4 |
由表 1和表 2可以看出, 与传统SVM所建预测模型相比, 基于混合优化算法的SVM所建预测模型对实际运行数据具有更优异的拟合能力。由此表明, 基于输入输出数据的单元机组协调控制系统数学模型符合火电厂的实际生产过程, 所建模型真实可靠。
经过处理后, 基于混合优化算法的SVM辨识所得机组负荷——主汽压力的数据模型为
| $ \left\{\begin{array}{c} \mathrm{y}_{1}(k)=1.99 y_{1}(k-1)-0.9898 y_{1}(k-2)- \\ 0.0006687 u_{1}(k-2)+ \\ 0.0006852 u_{1}(k-23)- \\ 0.001671 u_{2}(k-1)+ \\ 0.00166 u_{2}(k-2) \\ \mathrm{y}_{2}(k)=2.895 y_{2}(k-1)-2.79 y_{2}(k-2)+ \\ 0.8956 y_{2}(k-3)- \\ 0.00117 u_{1}(k-2)+ \\ 0.00008026 u_{1}(k-23)+ \\ 0.001147 u_{1}(k-24)+ \\ 0.9217 u_{2}(k-1)-1.839 u_{2}(k-2)+ \\ 0.9169 u_{2}(k-3) \end{array}\right. $ | (11) |
转换为CARIMA形式为
| $\left[\begin{array}{ll}A_{1}\left(z^{-1}\right) & \\ & A_{2}\left(z^{-1}\right)\end{array}\right] \cdot\left[\begin{array}{l}y_{1}(k) \\ y_{2}(k)\end{array}\right]= \\ \left[\begin{array}{cc}B_{11}\left(z^{-1}\right) & B_{12}\left(z^{-1}\right) \\ B_{21}\left(z^{-1}\right) & B_{2}\left(z^{-1}\right)\end{array}\right] \cdot\left[\begin{array}{c}u_{1}(k) \\ u_{2}(k)\end{array}\right]+\left[\begin{array}{c}\frac{\xi_{1}(k)}{\Delta} \\ \frac{\xi_{2}(k)}{\Delta}\end{array}\right]$ | (12) |
| $\left\{\begin{aligned} A_{1}\left(z^{-1}\right)=1 &-1.99 z^{-1}+0.9898 z^{-2} \\ A_{2}\left(z^{-1}\right)=& 1-2.895 z^{-1}+\\ & 2.79 z^{-2}-0.8956 z^{-3} \\ B_{11}\left(z^{-1}\right)=&-0.0006687 z^{-22}+\\ & 0.0006852 z^{-23} \\ B_{12}\left(z^{-1}\right)=&-0.001671 z^{-1}+\\ & 0.001662 z^{-2} \\ B_{21}\left(z^{-1}\right)=&-0.00117 z^{-22}+\\ & 0.00008026 z^{-23}+0.001147 z^{-24} \\ B_{22}\left(z^{-1}\right)=& 0.9217 z^{-1}-\\ & 1.839 z^{-2}+0.9169 z^{-3} \end{aligned}\right.$ | (13) |
4 结合GPC的仿真分析
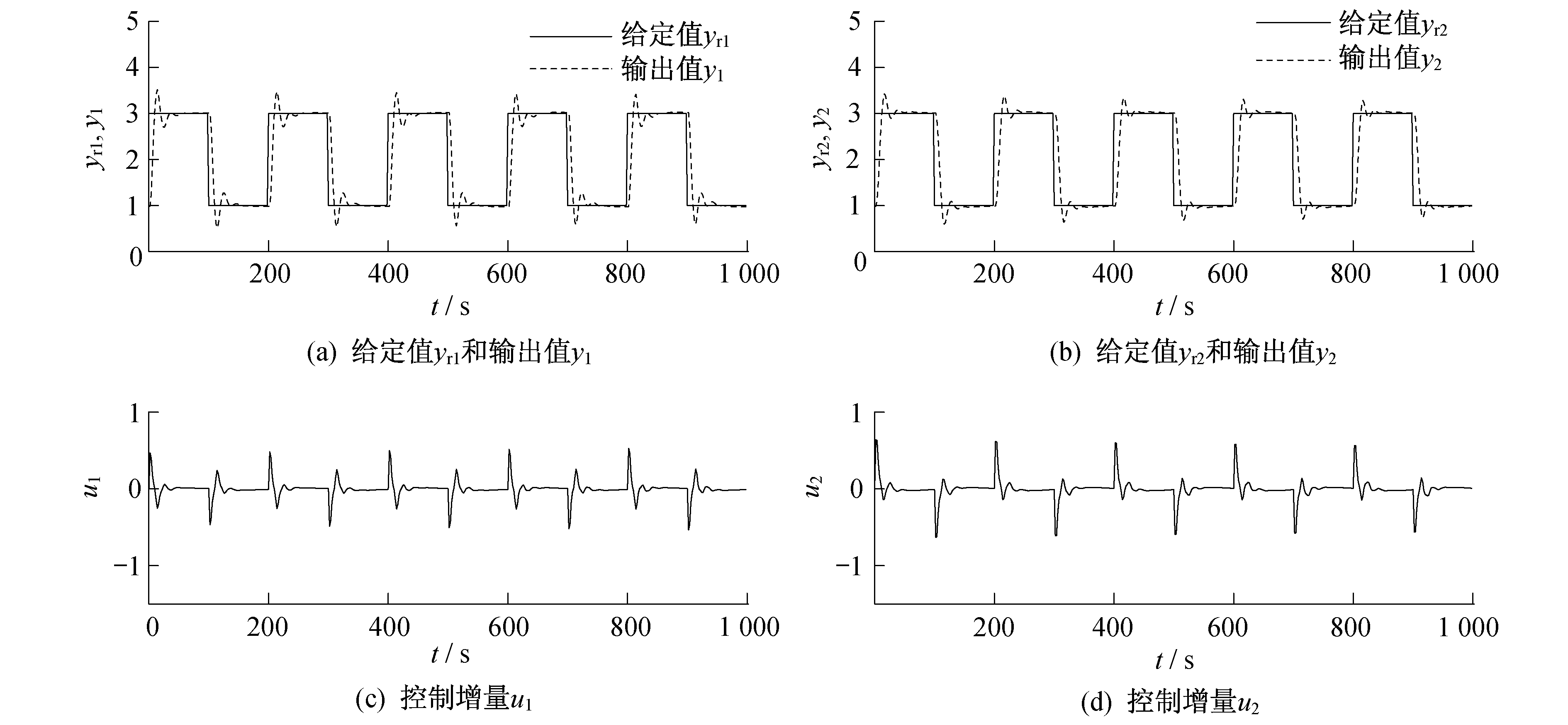
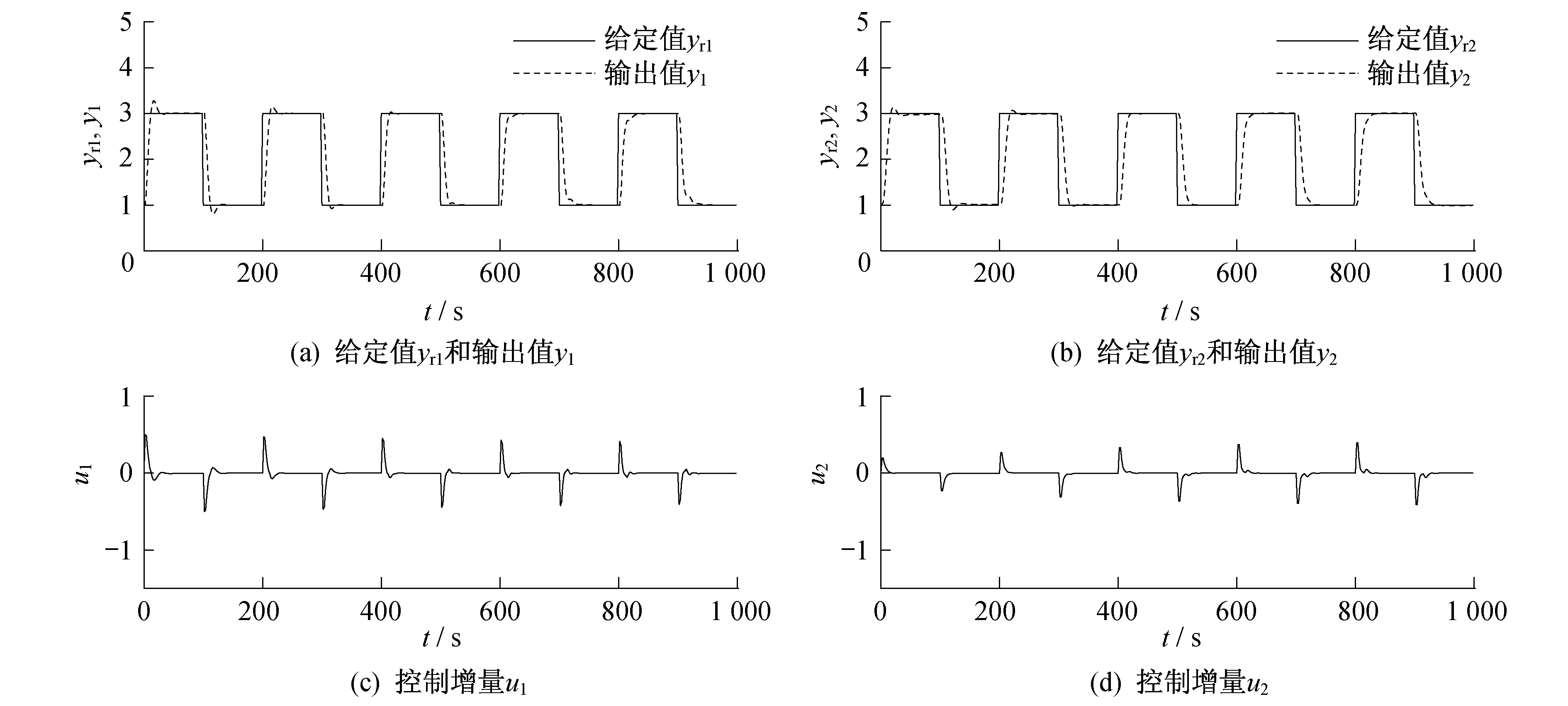
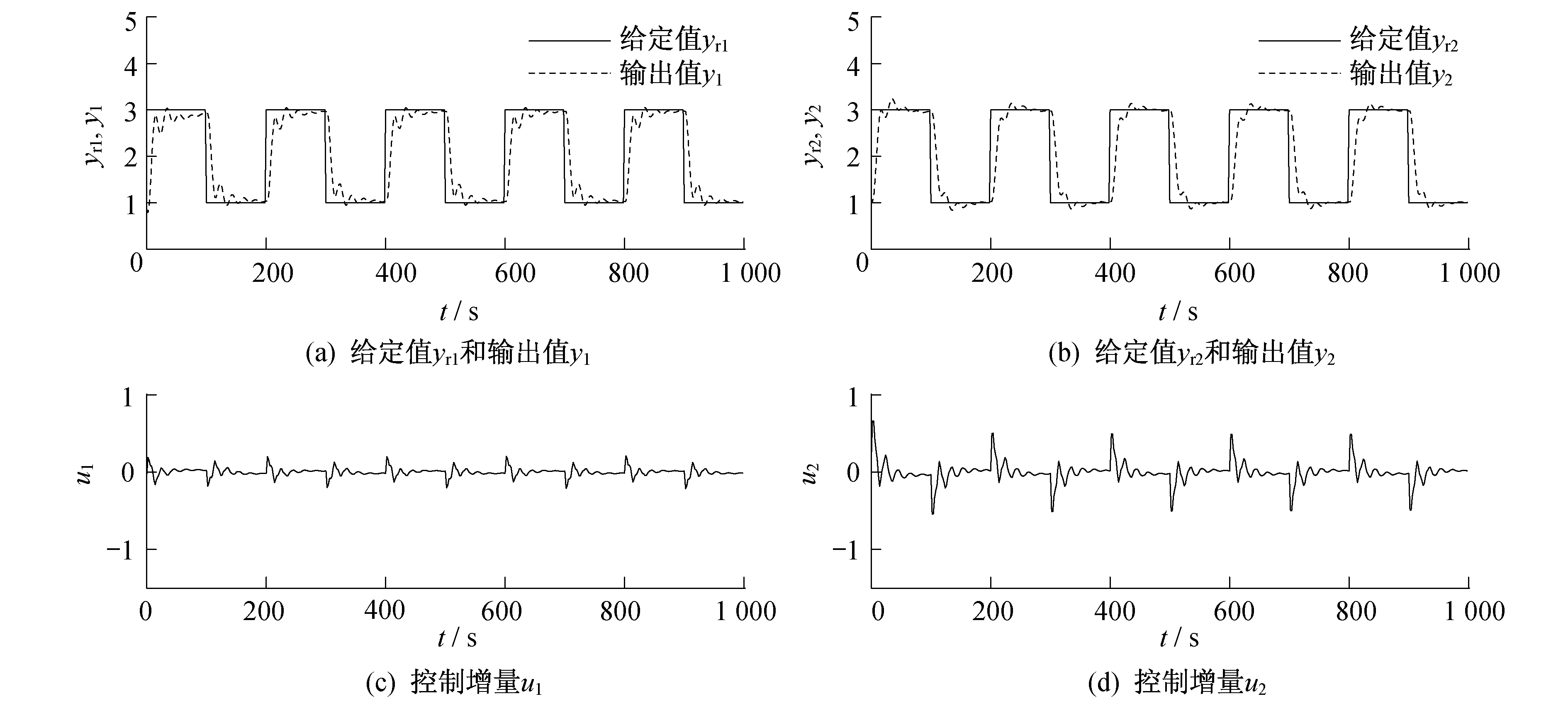
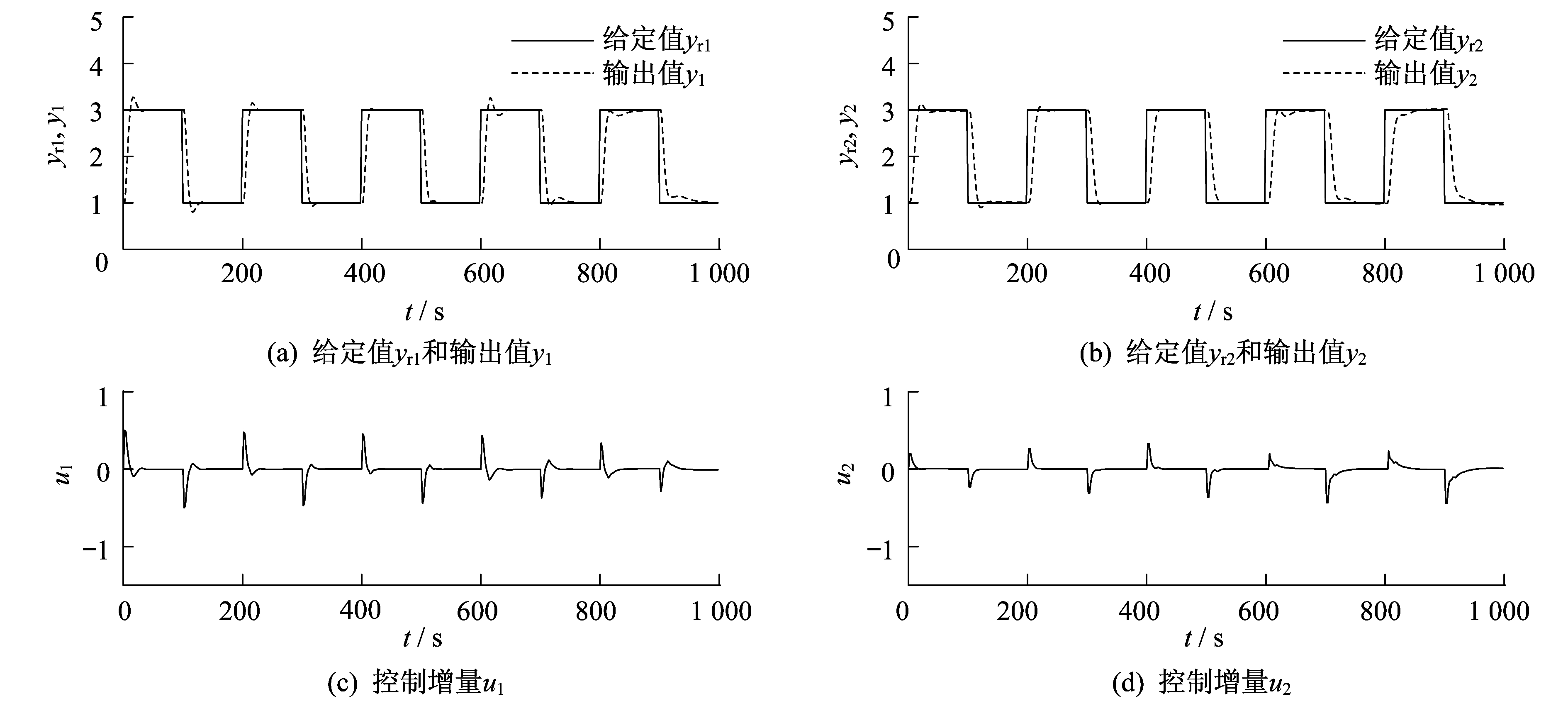
将上述所建的具有CARIMA结构形式的亚临界机组协调控制系统模型, 作为GPC的预测模型。GPC的隐式算法中各参数统一设置为:优化时域P=6;控制时域M=2;控制增量加权系数λ=0.75;柔化系数α=0.13。基于SVM的GPC对给定值的跟踪能力如图 3所示。基于混合算法SVM的GPC对给定值的跟踪能力如图 4所示。基于PID对给定值的跟踪能力如图 5所示。
由图 3~图 5可以看出:相比于传统的PID控制, 基于CARIMA模型的GPC对给定值的跟踪能力更强, 虽然存在一些超调, 但其上升时间大大减少, 应对给定值变化的响应速度更快, 调节时间短, 稳定后不存在稳态误差; 而基于混合算法优化的SVM与GPC算法的结合, 对给定值的跟踪能力更优越。
为了验证由于机组负荷工况点变化导致模型参数和时滞变化时的跟踪能力和抗干扰能力, 前600 s依然采用上述所建100%负荷工况点处模型, 600~1 000 s采用83.3%负荷工况点处单元机组模型[13], 即
| $G(s)=\left[\begin{array}{c}\frac{0.571(1-35 s)}{(1+189 s)(1+250 s)} \mathrm{e}^{-23} \\ \frac{18.6(1-35 s)}{(1+189 s)(1+250 s)(1+12 s)} \mathrm{e}^{-23}\end{array}\right. \\ \left.\begin{array}{c}\frac{-0.279}{1+250 s} \\ \frac{0.571(1-35 s)}{(1+189 s)(1+250 s)} \mathrm{e}^{-23}\end{array}\right]$ | (14) |
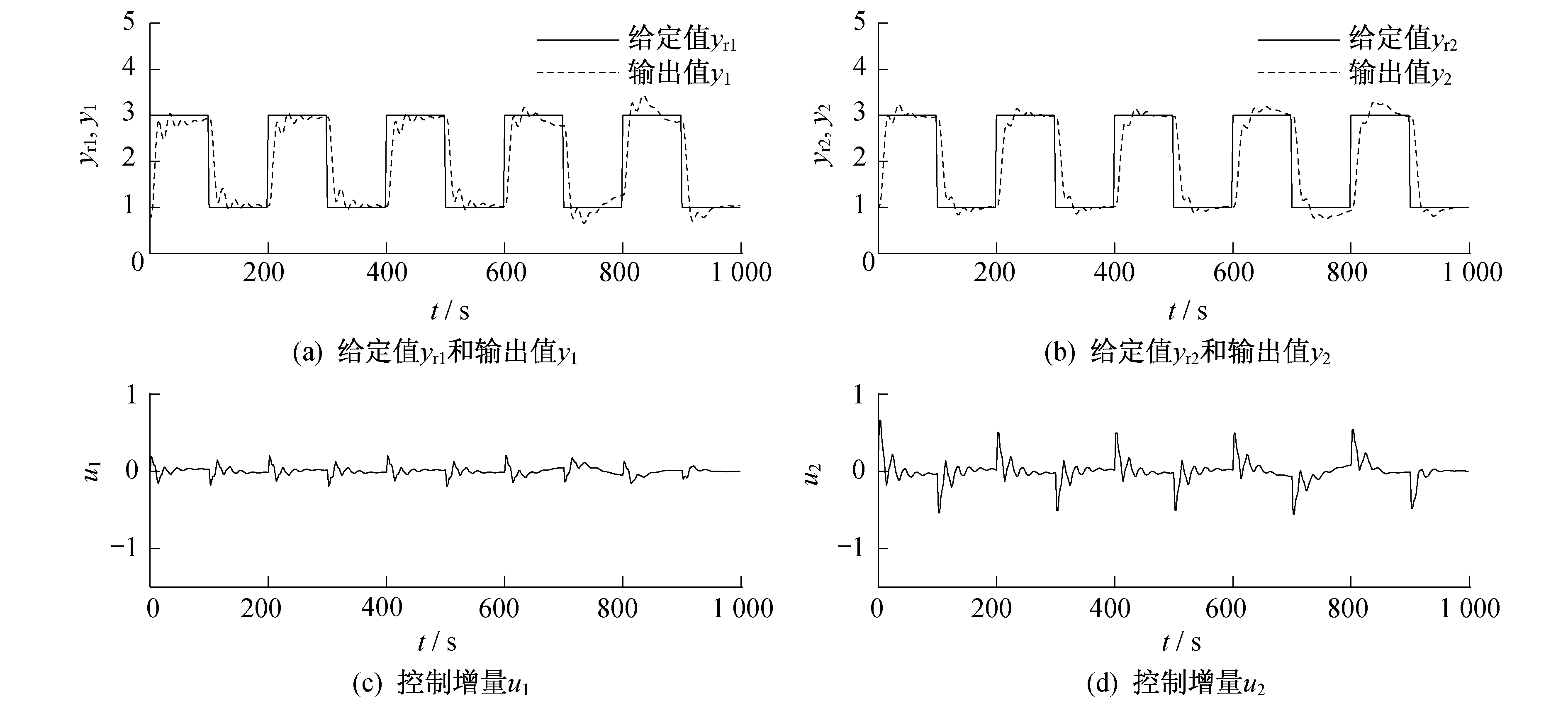
基于混合算法SVM的GPC抗干扰能力如图 6所示。基于PID的抗干扰能力如图 7所示。
由图 6和图 7可以看出, 当模型参数与时滞变化时, GPC对给定值的跟踪能力与应对模型变化时的抗干扰能力明显优于传统的PID控制。这是因为GPC起源于自校正控制, 继承了后者的特性。在实际控制中, 可以根据实际输入输出数据不断地实时预测模型参数, 及时调整最优控制律, 使控制系统始终保持在最佳运行状态。
5 结语
本文利用基于混合算法优化的SVM, 根据某机组的输入输出数据建立了亚临界机组协调控制系统对象模型。改进的算法提高了SVM建模的精度, 对电厂机组实际运行的机前压力和机组负荷数据有较好的拟合能力。所提出的基于SVM的GPC策略可以有效增强亚临界燃煤协调控制系统的稳定性和鲁棒性, 具有较强的抗干扰能力。
参考文献
-
[1]WU Z. Generalized predictive and fuzzy control in 600 MW supercritical unit coordinated control system[C]//2016 IEEE International Conference on Mechatronics and Automation. New York, USA, 2016: 3066-3075.
-
[2]基于神经网络预测控制的单元机组协调控制策略[J]. 动力工程, 2006, 26(3): 392-395.
-
[3]支持向量机算法在电厂中的应用[J]. 上海电力学院学报, 2013, 29(1): 5-8.
-
[4]郁磊, 史峰, 王辉, 等. MATLAB智能算法30个案例分析[M].北京: 北京航空航天大学出版社, 2011.
-
[5]基于支持向量机和BP神经网络的燃煤锅炉NOx排放预测[J]. 热能动力工程, 2016, 31(10): 104-108.
-
[6]MUSTAFFA Z, SULAIMAN M H. LS-SVM hyper—parameters optimization based on GWO algorithm for time series forecasting[C]//2015 4th International Conference on Software Engineering and Computer Systems(ICSECS). Hong Kong, China, 2015: 1033-1040.
-
[7]HUA L, HUANG L. Generalized predictive control based on LS-SVM inverse system method[C]//2010 8th World Congress on Intelligent Control and Automation. Guang Zhong, China, 2010: 1644-1652.
-
[8]QIANG W, YING Z. Wavelet neural network prediction algorithm based on improved implicit generalized predictive control[C]//2018 Chinese Control And Decision Conference(CCDC). Guang Zhong, China, 2018: 2100-2105.
-
[9]模型预测控制——现状与挑战[J]. 自动化学报, 2013, 39(3): 222-236.
-
[10]DILMEN E, BEYHAN S. State space LS-SVM for polynomial nonlinear state space model based generalized predictive control of nonlinear systems[C]//2018 IEEE Conference on Control Technology and Applications(CCTA). New York, USA, 2018: 1533-1538.
-
[11]群智能算法优化支持向量机参数综述[J]. 智能系统学报, 2018, 13(1): 70-84.
-
[12]HOU G, GONG L, HUANG C, et al. Improved constrained generalized predictive control for coordinated control system in supercritical unit[C]//2017 Chinese Automation Congress. Bei Jing, China, 2017: 1523-1529.
-
[13]660 MW机组负荷-压力非线性特性的分析[J]. 动力工程学报, 2005, 25(4): 533-536. DOI:10.3969/j.issn.1674-7607.2005.04.017