|
|
|
发布时间: 2019-10-10 |
|
|
|
|
收稿日期: 2019-03-01
基金项目: 上海市电站自动化技术重点实验室项目(13DZ2273800);上海市科学技术委员会地方能力建设项目(18020500900);上海市自然科学基金(核电风险评估中不确定性推理与关联机制研究-19ZR1420700)
中图法分类号: TM623
文献标识码: A
文章编号: 1006-4729(2019)05-0472-07
|
摘要
为保证核电站的安全经济运行, 对核电站常规岛的主要热力设备——加热器进行了基于经济性能的状态预警及劣化趋势的研究。首先, 建立基于加热器经济性能的状态综合评价模型, 量化其经济状态的动态变化过程, 将“异常”状态作为加热器经济性能的预警状态; 然后, 采用灰色预测和指数平滑的组合预测方法, 对加热器经济性能的劣化趋势进行预测, 以预估其经济状态转为“严重”的时间节点, 排除潜在故障, 提高检修效率, 降低维修成本; 最后, 在核电仿真平台插入典型的积聚型故障实例进行了验证, 结果证明了所作研究的可行性和有效性。
关键词
加热器; 经济性能; 状态预警; 趋势预测
Abstract
In order to ensure the safe and economic operation of the nuclear power plant, the research on the status alarm and deterioration trend based on the economic performance of the main thermal equipment of the conventional island in the nuclear power plant is proposed.Firstly, by establishing a state comprehensive evaluation model based on economic performance of the heater, the dynamic process of the economic state is quantified, and the "abnormal" state is used as the early warning state of the economic performance of the heater.Then, by using the combination forecasting method of gray prediction and exponential smoothing, the deterioration trend of the economic performance of the heater is estimated to predict the time node whose economic state turns into "serious", to eliminate potential failures, improve maintenance efficiency, and reduce maintenance costs.Finally, a typical accumulation fault instance is inserted into the nuclear power simulation platform for verification.The validity and feasibility of the research are proved in the results.
Key words
heater; economic performance; status alarm; trend prediction
目前, 关于核电设备的研究多集中于对一回路设备的状态监测与故障诊断, 如蒸汽发生器的破口事故等, 实际上, 二回路设备的运作状态也直接影响着整个电站的运行。加热器作为常规岛热力系统中关键的换热设备, 一旦发生劣化或是严重故障, 其自身的能量损耗势必增加, 则运行的热经济性大幅降低, 无法获得足够的热量来加热给水, 很大程度上会造成反应堆功率的扰动, 影响核电机组运行的安全性与稳定性。因此, 及时掌握加热器设备的运行状态, 对其进行状态预警, 并预测其劣化趋势十分重要。
现阶段对评价设备状态的研究较多, 主要涉及到提取评价指标、确定各指标权重、建立综合评价模型等方面。文献[1]采用主成分分析法提取出全新的综合评价指标, 并利用该指标对电站机组的运行状态进行了评估。文献[2]在模糊综合评判的基础上, 采用相对劣化度来表征状态变化, 由此建立了变压器的运行状态评估模型, 并验证了该方法的有效性。文献[3]提出并建立了一种动态变权层次分析的状态分析模型, 并利用数据证明该模型可对设备的内在机理进行有效表达。文献[4]在获取电厂设备参数的基础上, 采用证据融合理论建立了相应的状态评价模型, 并利用数据验证了该方法的可用性。
同样, 预测技术也得到了广泛应用。文献[5]采用支持向量机方法对不常用备件的需求进行了预测, 并建立了该方法的预测支持系统。文献[6]以核电站一回路作为研究对象, 采用灰色-马尔科夫的组合预测模型, 建立了趋势预测系统, 并通过实验数据证明了该方法的有效性。文献[7]将神经网络与灰色预测方法相结合, 建立了组合预测模型, 在往复泵故障趋势预测中获得了良好效果。文献[8]建立了指数平滑与非线性回归分析的组合预测模型, 提高了预测精度, 可在实际生产中应用于滑坡事件预报。
本文针对常规岛加热器进行了基于经济性能的状态预警与趋势预测的研究, 以全面评价加热器的经济动态, 确立其预警状态, 预估其劣化趋势, 以期为运行人员提供有效提示, 尽早尽快排除潜在隐患。
1 基于加热器经济性能的状态预警研究
1.1 表征加热器经济性能的指标提取
本文通过建立加热器的热经济性机理模型进行参数分析, 以提取表征其经济性能的关键指标, 综合考量其整体的经济情况, 确定加热器经济性能的预警状态。
由于目前核电站多采用自然循环蒸汽发生器, 而该种类的蒸汽发生器只产生饱和蒸汽, 即与给水进行热量交换加热给水的抽汽是湿蒸汽, 因此常规岛加热器的壳侧部分可简要划分为蒸汽冷凝段和疏水冷却段两个区域[9]。蒸汽冷凝段和疏水冷却段对应的能量平衡方程如下。
| $D_{\mathrm{w}}\left(h_{\mathrm{w} 2}^{\prime}-h_{\mathrm{w} 2}\right)=D_{\mathrm{c}}\left(h_{\mathrm{c}}-h_{\mathrm{ec}}\right)$ | (1) |
| $k_{1} F_{1} \Delta t_{\mathrm{m} 1}=D_{\mathrm{w}}\left(h_{\mathrm{w} 2}-h_{\mathrm{w} 2}^{\prime}\right)$ | (2) |
| $D_{\mathrm{w}}\left(h_{\mathrm{w} 2}^{\prime}-h_{\mathrm{w} 1}\right)=D_{c}\left(h_{\mathrm{ec}}-h_{\mathrm{ec}}^{\prime}\right)$ | (3) |
| $k_{2} F_{2} \Delta t_{\mathrm{m} 2}=D_{\mathrm{w}}\left(h_{\mathrm{w} 2}^{\prime}-h_{\mathrm{w} 1}\right)$ | (4) |
式中:Dw——给水流量;
hw2, h′w2——加热器和疏冷段出口水焓值;
Dc, hc——抽汽流量和抽汽焓值;
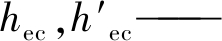 蒸汽冷凝段和疏水冷却段疏水焓值;
蒸汽冷凝段和疏水冷却段疏水焓值;
k1, k2——蒸汽冷凝段和疏水冷却段的传热系数;
F1, F2——蒸汽冷凝段和疏水冷却段的有效传热面积;
Δtm1, Δtm2——蒸汽冷凝段和疏水冷却段的对数平均温差;
hw1——给水入口水焓值。
根据式(1)~式(4), 考虑散热效率, 可得其整体的热经济性机理模型为
| $ D_{\mathrm{w}}\left(h_{\mathrm{w} 2}-h_{\mathrm{w} 1}\right)=\eta_{i} D_{\mathrm{c}}\left(h_{\mathrm{c}}-h_{\mathrm{ec}}^{\prime}\right) $ | (5) |
式中:ηi——第i号加热器的散热效率, i=1, 2, 3, …, n(n为加热器的数量)。
根据式(5), 可得与加热器散热效率直接相关的运行参数, 即
| $ \eta_{i}=f\left(h_{\mathrm{w} 2}, h_{\mathrm{w} 1}, h_{c}, h_{\mathrm{ec}}^{\prime}, D_{\mathrm{w}}, D_{\mathrm{c}}\right) $ | (6) |
式中:f——等式两侧变量之间呈现一定的函数关系。
由于给水流量非直接测点, 而焓值可根据温度和压力值推算得到, 即Tw2=f(pw2, hw2), 而抽汽量与抽汽压力密切相关, 故可获得与散热效率相关的可测参数, 即
| $\eta_{i}=f\left(T_{\mathrm{w} 2}, T_{\mathrm{w} 1}, T_{\mathrm{ec}}, P_{\mathrm{c}}, P_{\mathrm{gin}}\right)$ | (7) |
式中:Tw2, Tw1——给水出口和入口温度;
Tec——加热器疏水出口温度;
Pc——抽汽口压力;
Pgin——加热器进汽压力。
根据式(7), 结合对标手册、运行资料与文献[11-12], 从中可提取出用于加热器经济状态综合评价的参数指标。其数学模型如表 1所示。
表 1
某高压加热器的经济运行指标及其描述
| 经济指标 | 数学模型 |
| 上端差/K | Ttd=Tsat-Tw2 |
| 下端差/K | Dca=Tec-Tw1 |
| 给水温升/K | Toi=Tw2-Tw1 |
| 抽汽压损/% | Ploss=(Pc-Pgin)/Pgin×100% |
| 注:Ttd—上端差; Tsat—加热器进口蒸汽压力下的饱和温度(可通过压力值和焓值查表得到); Dca—下端差; Toi—给水温升; Ploss—抽汽压损。 | |
本文基于AP1000核电仿真系统, 取常规岛正常运行的100%工况, 通过分析大量的实验结果发现, 各经济指标的波动范围很小, 接近于静态运行。故根据统计学原理, 各经济指标选取在多次实验下的平均值作为研究工况下的标准值。当评价指标的实时值与标准值发生偏离时, 说明加热器的经济性能已经降低; 无论该实时值指标的变化情况是增大还是减小, 均为非最优运行状态; 而偏离标准值的程度越高, 即在数学意义上, 两者之间的“距离”越大, 相似程度越低, 则经济性能下降得越多, 加热器的劣化程度越严重。
其中, 两个因素之间的相似程度可用“关联度”概念进行考量。因此, 本文采用灰色关联度分析法对加热器设备的实时经济状态与最优状态的差距进行量化, 以研究加热器经济性能的动态变化过程, 并为后续预测其发展趋势打下基础。
1.2 灰色关联度分析
灰色关联度分析法是通过计算待研究数列与给定参考数列之间的几何相似度, 并根据获得的相似度来衡量所研究数列与参考数列之间的关联度。若所研究数列与参考数列的几何形状相似性很高, 说明两者的变化态势较为相似, 有相对大的关联度。利用灰色关联度进行状态评价的步骤如下。
步骤1 根据实际选定的指标体系, 确定原始待比较矩阵, 并给出标准参考数列。将数据分为m组(m表示指标的运行时长, 以秒为单位), 涉及指标为n个, 用xij表示第i组数据第j个指标的值, 故原始数据矩阵可写为
| $ \boldsymbol{X}=\left(\begin{array}{c} X_{1} \\ X_{2} \\ \vdots \\ X_{i} \\ \vdots \\ X_{m} \end{array}\right)=\left[\begin{array}{cccccc} x_{11} & x_{12} & \cdots & x_{1 j} & \cdots & x_{1 n} \\ x_{21} & x_{22} & \cdots & x_{2 j} & \cdots & x_{2 n} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ x_{i 1} & x_{i 2} & \cdots & x_{i j} & \cdots & x_{i n} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ x_{m 1} & x_{m 2} & \cdots & x_{m j} & \cdots & x_{m n} \end{array}\right] \\ (1 \leqslant i \leqslant m, 1 \leqslant j \leqslant n)$ | (8) |
其中, 标准参考数列可表示为X0=(x01, x02, …, x0j, …, x0n)。
步骤2 由于众多指标之间存在差异, 在数值的绝对值大小上表现不同, 故需先消除各状态量的量纲、数量级和因素类型的影响, 即进行标准化处理, 并记标准化处理后的数据矩阵为
| $ \boldsymbol{Z}=\left(\begin{array}{c} Z_{0} \\ Z_{1} \\ \vdots \\ Z_{i} \\ \vdots \\ Z_{m} \end{array}\right)=\left[\begin{array}{cccccc} z_{01} & z_{02} & \cdots & z_{0 j} & \cdots & z_{0 n} \\ z_{11} & z_{12} & \cdots & z_{1 j} & \cdots & z_{1 n} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ z_{i 1} & z_{i 2} & \cdots & z_{i j} & \cdots & z_{i n} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ z_{m 1} & z_{m 2} & \cdots & z_{m j} & \cdots & z_{m n} \end{array}\right] ,\\ (1 \leqslant i \leqslant m, 1 \leqslant j \leqslant n)$ | (9) |
式中:Z0——标准化处理后的参考数列, Z0=(z01, z02, …, z0j, …, z0n)。
步骤3 对于通过标准化处理后的数据, 对应计算待比较序列与参考数列差值的绝对值, 即
| $\left|Z_{i}-Z_{0}\right|=\left|z_{i j}-z_{0 j}\right|, i=1,2,3, \cdots, m \\ j=1,2,3, \cdots, n$ | (10) |
步骤4 通过式(10)将待比较序列与参考序列之间每一组相对应的元素取出, 计算其关联度
| $\xi_{i j}=\frac{\min \limits_{i=1}^{m}\left\{\min \limits_{j=1}^{n}\left(\left|z_{i j}-z_{0 j}\right|\right)\right\}+\eta \cdot \max \limits_{i=1}^{m}\left\{\max \limits_{j=1}^{n}\left(\left|z_{i j}-z_{0 j}\right|\right)\right\}}{\left|z_{i j}-z_{0 j}\right|+\max\limits_{i=1}^{m}\left\{\max \limits_{j=1}^{n}\left(\left|z_{i j}-z_{0 j}\right|\right)\right\}}$ | (11) |
式中:ξij——关联系数, 是一个小于1的正数, 反映了第i个比较序列Xi与参考序列X0在第j个指标上的关联程度;
η——分辨系数, 其值在区间(0, 1)之间(η的值越小, 说明关联系数间的差距越大, 则分辨能力越强, 通常取0.5。
步骤5 计算关联度。对于各待比较序列, 分别计算其与参考序列对应元素的关联系数的均值, 以反映各待比较序列与参考序列的关联程度, 记为
| $\boldsymbol{P}=\left(p_{01}, p_{02}, \cdots, p_{0 i}, \cdots, p_{0 m}\right)^{\mathrm{T}}, \\ i=1,2,3, \cdots, m$ | (12) |
其中,
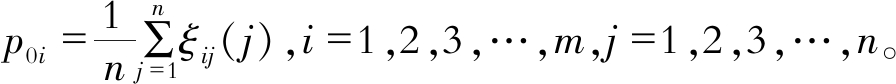
可根据要求对各个指标赋予权重, 记为W=(w1, w2, w3, …, wj, …, wn)T, j=1, 2, 3, …, n。此时,
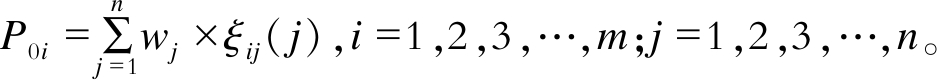 本文选用熵值法来确定各经济指标的权重[13]。各指标权重满足
本文选用熵值法来确定各经济指标的权重[13]。各指标权重满足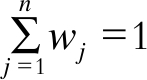 且wj∈[0, 1], j=1, 2, 3, …, n。
且wj∈[0, 1], j=1, 2, 3, …, n。
步骤6 依据各待比较对象的关联度计算结果, 得出综合的关联度。
1.3 加热器经济预警状态的确立
基于已提取的经济性能指标, 对加热器经济状态综合评价的结果采用分级描述, 同时为量化加热器抽象的经济状态, 将灰色关联度与评价等级建立了一一对应的映射关系, 如表 2所示。
表 2
加热器状态评价等级与灰色关联度的对应关系
| 序号 | 状态评价等级 | 对应灰色关联度 | 对应状态描述 |
| 1 | 正常 | 1~0.8 | 设备状态非常好 |
| 2 | 注意 | 0.79~0.61 | 设备状态较好, 可以继续运行, 并加强监视 |
| 3 | 异常 | 0.6~0.4 | 设备劣化态势加重, 需及时确认是否存在故障 |
| 4 | 严重 | < 0.4 | 劣化严重, 发生功能故障的概率极大 |
由此, 本文建立了基于加热器经济性能的状态综合评价模型, 即
| $ P_{\mathrm{t}}=\sum\limits_{i=1}^{n} w_{i} \times \xi_{i}, i=1,2,3, \cdots, n $ | (13) |
式中:Pt——评价得出的总体灰色关联度;
n——用于状态预诊断的经济指标的数量, 本文取n=4, 分别为上端差、下端差、给水温升及抽汽压损;
wi——第i个经济指标所占的权重, 该值通过熵值法确定;
ξi——第i个经济指标的关联系数。
为避免加热器发展为故障概率极高的“严重”状态(即灰色关联度下降至0.4), 本文设定, 当状态综合评价的结果为“异常”时(即灰色关联度下降至0.6), 视作处于预警状态。此时加热器已发生了一定程度的劣化, 故需对其劣化趋势进行预测, 以确定状态转变为“严重”的时间节点, 及时估计在“异常”与“严重”的状态节点之间的检修时长, 有利于更好地进行检修决策, 确保在此预估时间区间内完成各项检修, 保证加热器的经济和安全运行。
2 基于加热器经济性能的劣化趋势预测
2.1 灰色预测GM(1, 1)简介
GM(1, 1)模型的基本思想是:对原始数据序列进行累加的运算处理, 处理后的数据序列中含某种内在规律, 通过回归的方法, 根据处理后的数据拟合微分方程, 求得该方程的离散解, 再将数据通过累减的方式还原, 求得最终的预测值。预测值即是对发展过程的定量化预测[14]。
建立灰色预测GM(1, 1)模型的过程如下。
设原始非负数据序列X(0)为GM(1, 1)建模序列
| $ X^{(0)}=\left\{x_{1}^{(0)}, x_{2}^{(0)}, x_{3}^{(0)}, \cdots, x_{n}^{(0)}\right\} $ | (14) |
进行一次累加, 从而得到新的数据序列, 即X(1)为X(0)的1-AGO序列。
| $ X^{(1)}=\left\{x_{1}^{(1)}, x_{2}^{(1)}, x_{3}^{(1)}, \cdots, x_{n}^{(1)}\right\} $ | (15) |
其中,
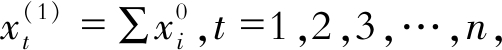 即
即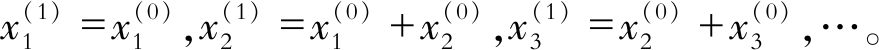
X(1)的均值序列Z(1)为
| $ Z^{(1)}=\left\{z_{2}^{(1)}, z_{3}^{(1)}, \cdots, z_{n}^{(1)}\right\} $ | (16) |
其中,
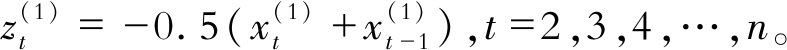
则GM(1, 1)的灰色微分方程模型为
| $ x_{t}^{(0)}+a z_{t}^{(1)}=u $ | (17) |
式中:
 灰导体;
灰导体;
a——发展系数, 主要控制系统发展态势的大小;
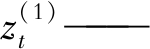 白化背景值;
白化背景值;
u——灰色作用量, 其大小反映着数据变化的关系。
可利用最小二乘法估计求出参数a和u。
| $\frac{\mathrm{d} x^{(1)}}{\mathrm{d} t}+a x^{(1)}=u$ | (18) |
求解此方程得到
| $ \begin{aligned} \hat{x}_{t}^{(1)}=& \left[x_{0}^{(1)}-\frac{\hat{u}}{\hat{a}}\right] \mathrm{e}^{-\hat{a} t}+\frac{\hat{u}}{\hat{a}}, \\ & t=1,2,3, \cdots, n \end{aligned} $ | (19) |
求解该灰色微分方程, 即可求得灰色GM(1, 1)模型的时间响应函数
| $ \begin{array}{c} \hat{x}_{t+1}^{(1)}=\left[x_{1}^{(0)}-\frac{\hat{u}}{\hat{a}}\right] \mathrm{e}^{-\hat{a} t}+\frac{\hat{u}}{\hat{a}}, \\ t=1,2,3, \cdots, n \end{array} $ | (20) |
取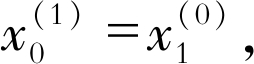 则
则
| $ \begin{array}{c} \hat{x}_{t+1}^{(1)}=\left[x_{0}^{(1)}-\frac{\hat{u}}{\hat{a}}\right] \mathrm{e}^{-\hat{a} t}+\frac{\hat{u}}{\hat{a}}, \\ t=1,2,3, \cdots, n \end{array} $ | (21) |
由式(21)对新的数据序列进行预测, 并通过一次性累减生成得到原始数据序列的预测模型为
| $ \hat{x}_{t+1}^{(0)}=\hat{x}_{t+1}^{(1)}-\hat{x}_{t}^{(1)}, t=1,2,3, \cdots, n $ | (22) |
2.2 指数平滑法
由于加热器的劣化为积累过程, 故需合理利用历史数据。可以加入指数平滑法来及时修正灰色预测结果, 以提高预测精度。指数平滑法的基本思想是:离预测时刻越近的数据, 其权重设定越大, 反之越小, 而权数的变化由近到远按指数规律递减[15]。为准确预测加热器经济状态的演变趋势, 本文采用三次指数平滑法, 具体为
| $ \left\{\begin{array}{l} S_{t}^{(1)}=a y_{t}+(1-a) S_{t-1}^{(1)} \\ S_{t}^{(2)}=a S_{t}^{(1)}+(1-a) S_{t-1}^{(2)} \\ S_{t}^{(3)}=a S_{t}^{(2)}+(1-a) S_{t-1}^{(3)} \end{array}\right. $ | (23) |
| $\hat{Y}_{t+1}=a_{t}+b_{t} \hat{Y}_{t}+c_{t} \hat{Y}_{t}^{2}$ | (24) |
| $ \left\{\begin{array}{l} a_{t}=3 S_{t}^{(1)}-S_{t}^{(2)}+S_{t}^{(3)} \\ b_{t}=\frac{\alpha}{2(1-\alpha)^{2}}\left[(6-5 \alpha) S_{t}^{(1)}-\right. \\ 2(5-4 \alpha) S_{t}^{(2)}+(4-3 \alpha) S_{t}^{(3)} \\ c_{t}=\frac{\alpha^{2}}{2(1-\alpha)^{2}}\left[S_{t}^{(1)}-2 S_{t}^{(2)}+S_{t}^{(3)}\right] \end{array}\right. $ | (25) |
式中:
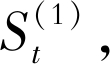
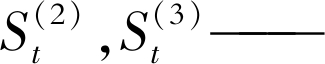 第t期的一次指数平滑值, 右上角标表示指数平滑的次数;
第t期的一次指数平滑值, 右上角标表示指数平滑的次数;
α——加权系数(即平滑系数), 取值在0~1之间;
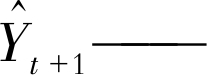 第t+1期的预测值;
第t+1期的预测值;
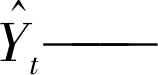 第t期的预测值。
第t期的预测值。
2.3 组合预测模型的建立
本文将灰色预测和指数平滑的预测值各赋予一定权重, 建立了组合预测模型, 即
| $x_{\mathrm{pre}}=\theta \cdot x_{\mathrm{gm}}+\beta \cdot x_{\mathrm{th}} ; \\ \theta+\beta=1$ | (26) |
式中:xpre——组合预测值;
θ, β——xgm和xth的对应权重;
xgm——灰色预测GM(1, 1)模型的预测值;
xth——三次指数平滑的预测值。
3 传热管结垢初始预警
传热管结垢是典型的积聚型故障, 其清洁度在0~1之间, 越接近1, 污垢越少; 反之, 则污垢越多。本文参考现有污垢热阻与时间的数学模型[16], 将时间作为自变量x, 清洁度作为因变量y, 对两者之间的关系进行数学建模, 模拟加热器实际的结垢过程。
| $y=0.25+0.7 \mathrm{e}^{-0.025 x}$ | (27) |
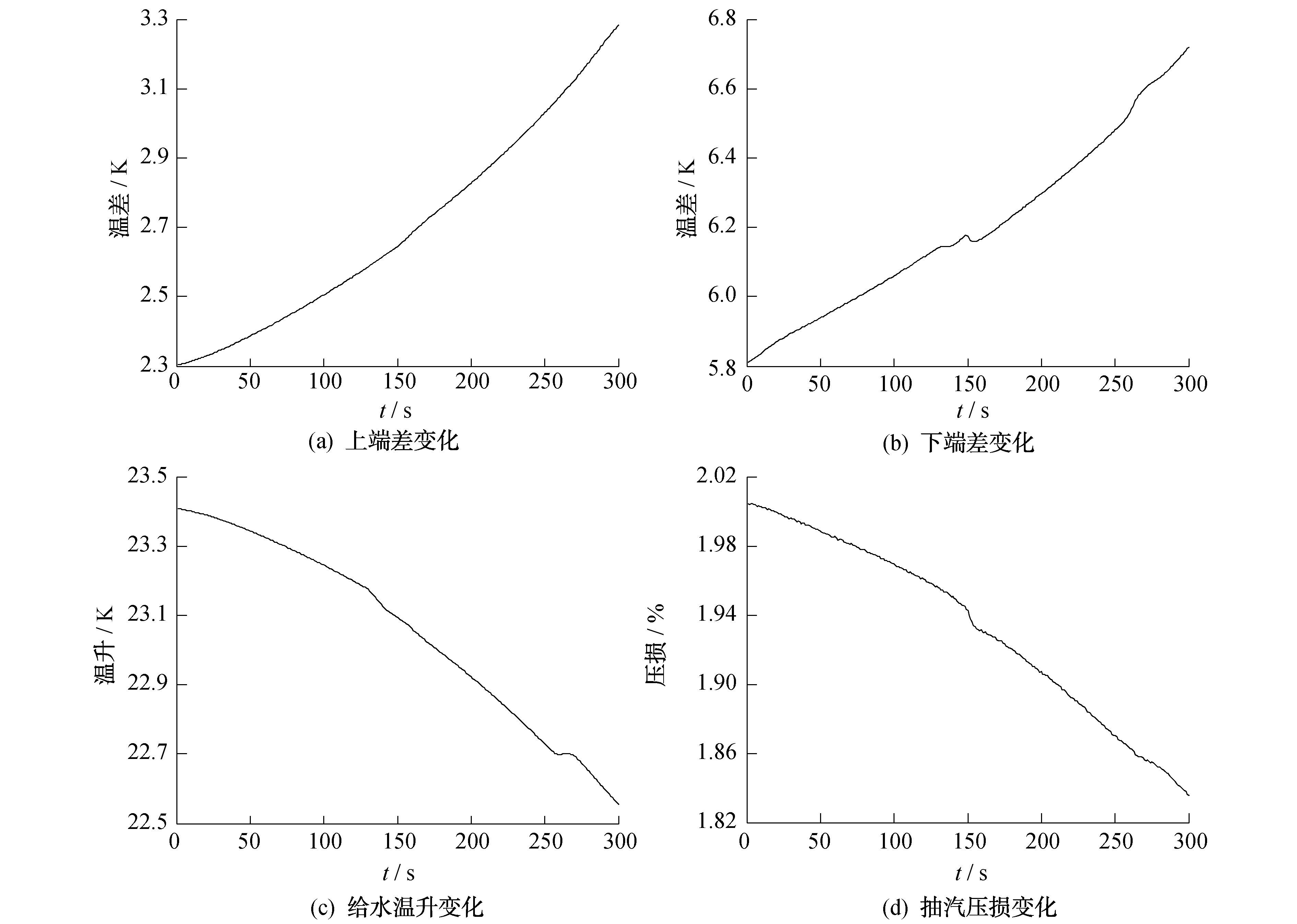
在核电仿真系统的某高压加热器中按式(27)插入结垢模型, 其中传热管的初始清洁度为1, 行程时间设为300 s, 然后运行该仿真系统, 可得到加热器相关参数的变化曲线。
3.1 基于经济性能的状态预警
首先确定了某高压加热器在100%工况下正常运行时各经济指标的标准值, 如表 3所示。
表 3
100%工况下正常运行时某高压加热器各经济指标标准值
| 经济指标 | 上端差 | 下端差 | 给水温升 | 抽汽压损/% |
| K | ||||
| 标准值 | 2.4 | 5.3 | 23.5 | 2.08 |
然后在100%工况下正常运行的某高压加热器中插入传热管结垢的故障模型, 各经济指标的变化曲线如图 1所示。
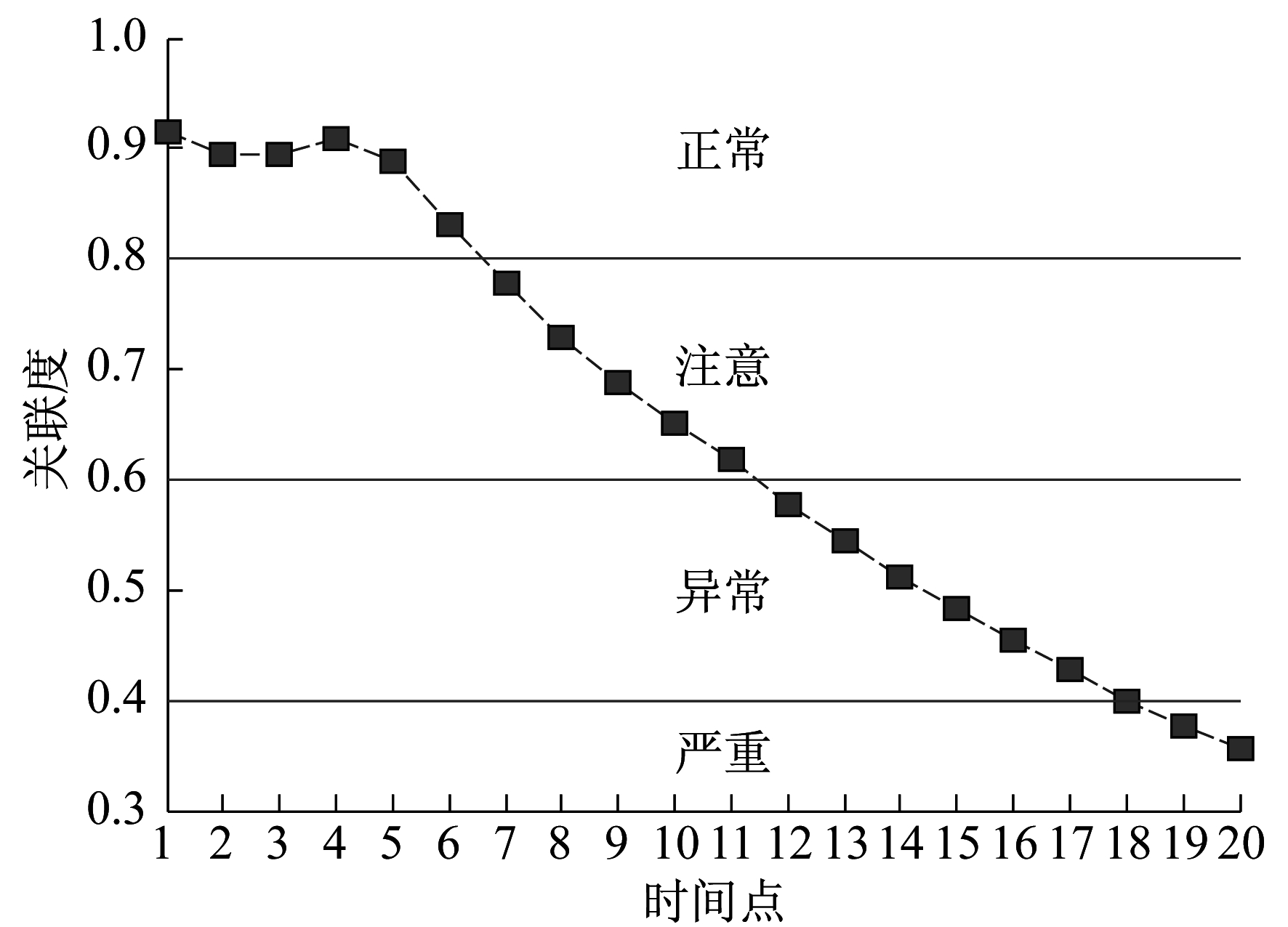
对某高压加热器的经济状态进行综合评价。由于运行时间较长, 为如实表现各参数变化情况, 在300 s时间序列中等间隔选取20组时间点进行分析, 如图 2所示。
由图 2可知, 在运行至t=12(即实际运行时间为180 s)时, 加热器各经济指标实时值与标准值之间的关联度已经下降到0.577, 对应的状态综合评价结果为“异常”, 表明此时加热器已处于预警状态, 已发生一定程度的劣化。
3.2 劣化趋势预测
本文取图 2中t=5~20的16组数据(即实际运行时间为第75~180 s)作为待用数据, 其中前8组作为用于建模的历史数据, 后8组作为检验预测精度的历史数据。将“异常”预警状态作为预测起始点, 对某高压加热器经济性能的劣化趋势进行预测。
(1) 指数平滑法预测 采用了使均方误差最小的最优搜索算法, 确定平滑系数α的值为0.472。
(2) GM(1, 1)灰色预测 本文对所建立的灰色预测模型进行预测精度考评, 计算可得其后验方差比为5.0e-03, 小误差概率为1。根据灰色预测模型的评判标准, 可知该模型精度等级为良好, 证明其具有可用性。
(3) 组合预测 本文取80%的灰色预测值和20%的指数平滑预测值进行加权平均, 得到新的组合预测值。
3种预测的具体结果如表 4所示。
表 4
各方法的预测结果
| 时间点 | 实际值 | 指数平滑预测值 | 灰色预测值 | 组合预测值 |
| 9 | 0.5453 | 0.5471 | 0.5441 | 0.5447 |
| 10 | 0.5128 | 0.5163 | 0.5126 | 0.5133 |
| 11 | 0.4823 | 0.4856 | 0.4829 | 0.4834 |
| 12 | 0.4539 | 0.4547 | 0.4549 | 0.4548 |
| 13 | 0.4287 | 0.4239 | 0.4285 | 0.4276 |
| 14 | 0.3989 | 0.3930 | 0.4037 | 0.4015 |
| 15 | 0.3766 | 0.3621 | 0.3803 | 0.3767 |
| 16 | 0.3555 | 0.3311 | 0.3582 | 0.3528 |
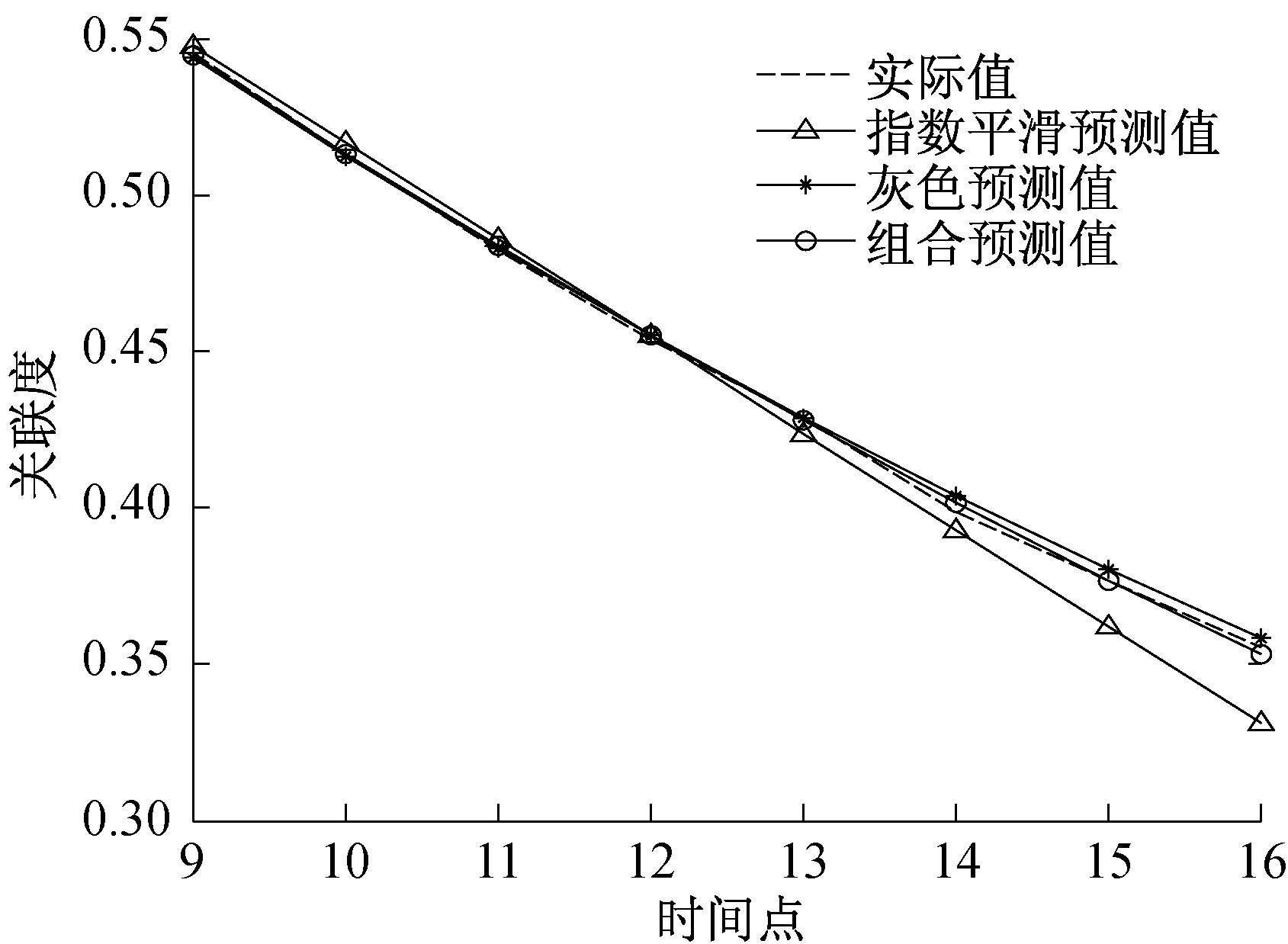
3种方法的预测值曲线如图 3所示。
为检验预测效果, 采用考量指标对各预测方法进行了比较, 结果如表 5所示。
表 5
各预测方法的预测效果比较
| 预测方法 | 均方误差 | 平均绝对误差 | 平均相对误差 |
| 指数平滑 | 4.380 4e-05 | 0.007 4 | 0.015 7 |
| 灰色预测 | 5.862 5e-06 | 0.001 8 | 0.023 3 |
| 组合预测 | 2.326 4e-06 | 0.001 2 | 0.002 9 |
由表 5可知, 组合预测的效果最佳。因此, 本文以组合预测结果为准, 对加热器进行检修决策:当某高压加热器发生此次故障时, 在180 s时进入“异常”的预警状态, 且很可能在210 s时进入“严重”状态, 此时加热器发生功能性故障的概率极大, 需在210 s的时间节点前及时修正检修计划并加以实施。
4 结语
本文对核电站常规岛加热器进行了基于经济性能的状态预警和劣化趋势预测的研究。通过建立加热器经济性能状态综合评价的模型, 量化了其经济状态的变化过程, 确立了其经济性能的预警状态, 并对加热器的劣化趋势进行组合预测, 从而进行检修决策, 及时修正加热器的检修计划, 优化检修策略, 提高检修效率。通过实例验证了本文所建模型的可行性和有效性。
参考文献
-
[1]采用主成分分析法综合评价电站机组的运行状态[J]. 动力工程学报, 2008, 28(4): 548-551. DOI:10.3321/j.issn:1000-6761.2008.04.011
-
[2]基于模糊综合评判的电力变压器运行状态评估模型[J]. 电力系统自动化, 2008, 32(3): 70-75. DOI:10.3321/j.issn:1000-1026.2008.03.017
-
[3]基于动态变权层次分析法的电网设备状态评价[J]. 电子测试, 2015(4): 27-29. DOI:10.3969/j.issn.1000-8519.2015.04.011
-
[4]卫平宝.基于数据融合的设备参数劣化分析与状态评价[D].保定: 华北电力大学, 2006.
-
[5]王文.基于支持向量机的不常用备件需求预测方法研究[D].武汉: 华中科技大学, 2006.
-
[6]于竹君.核动力设备状态趋势预测方法研究[D].哈尔滨: 哈尔滨工程大学, 2007.
-
[7]基于灰色-神经网络的往复泵状态监测和趋势预测研究[J]. 中国安全生产科学技术, 2013, 9(1): 79-84.
-
[8]基于指数平滑法与回归分析相结合的滑坡预测[J]. 岩土力学, 2007, 28(8): 1725-1728. DOI:10.3969/j.issn.1000-7598.2007.08.037
-
[9]核电站给水加热器建模与仿真[J]. 应用科技, 2011, 38(6): 67-72. DOI:10.3969/j.issn.1009-671X.2011.06.015
-
[10]加热器上端差对机组能效影响的分析研究[J]. 汽轮机技术, 2014, 56(5): 379-381. DOI:10.3969/j.issn.1001-5884.2014.05.019
-
[11]蒋伟莉.汽轮机组热力系统加热器性能分析及流场数值研究[D].南京: 东南大学, 2015.
-
[12]加热器抽汽压损偏离目标值对机组热经济性影响的定量分析[J]. 汽轮机技术, 2011, 53(4): 264-266. DOI:10.3969/j.issn.1001-5884.2011.04.007
-
[13]熵值法在滚动轴承选型灰色优化决策中的应用[J]. 轴承, 2009(12): 5-7. DOI:10.3969/j.issn.1000-3762.2009.12.002
-
[14]付辉.基于灰色预测模型和层次分析法的高校招生数据分析与研究[D].重庆: 重庆交通大学, 2013.
-
[15]苗开超.基于指数平滑模型的农产品价格预测研究[D].合肥: 合肥工业大学, 2009.
-
[16]油田集输系统换热器中污垢热阻预测研究[J]. 北京石油化工学院学报, 2010, 18(4): 51-54. DOI:10.3969/j.issn.1008-2565.2010.04.012