|
|
|
发布时间: 2019-10-10 |
|
|
|
|
收稿日期: 2019-03-06
基金项目: 上海市电站自动化技术重点实验室项目(13DZ2273800);上海市科学技术委员会地方能力建设项目(18020500900);上海市自然科学基金(19ZR1420700)
中图法分类号: TM615
文献标识码: A
文章编号: 1006-4729(2019)05-0479-07
|
摘要
电池储能系统具有快速、精确的功率响应能力, 有利于电厂更好地跟踪自动发电控制指令, 更高效地完成电网自动发电控制目标。由于储能系统的建设成本比较昂贵, 因此建立有效的储能电池经济性评估方法具有重要意义。首先提出了辅助火电机组参与调频的控制策略和分段调频的控制策略; 然后利用灰色模型算法建立了电池容量的衰减模型, 得出了对储能系统健康度的预测方法; 最后基于两种控制策略, 完成了对储能系统参与调频的经济性评价和比较。
关键词
储能系统; 自动发电控制; 健康度预测; 灰色模型算法; 雨流计数法; 电厂调频经济性
Abstract
The battery energy storage system has a fast and accurate power response capability and is beneficial for the power plant to better track the automatic generation control (AGC) command and complete the grid AGC control target more efficiently.Since the construction cost of the energy storage system is relatively high, it is of great significance to establish an effective method for economic evaluation of energy storage batteries.A control strategy for auxiliary thermal power units to participate in frequency modulation and a control strategy for subsection frequency modulation are proposed.Then a gray model algorithm is used to establish the attenuation model for battery capacity, and a prediction method for the health of energy storage systems is derived.Finally, two control methods are used.The strategy completed the research on the economic evaluation of energy storage system participation in FM.
Key words
energy storage system; automatic generation control; health forecast; grey model algorithm; rainflow counting method; power plant frequency modulation economy
随着电力需求的增长和电力企业市场化改革的推行, 电力系统的运行和需求发生了巨大的变化, 电力系统对储能的需求日益增大[1]。储能以其灵活的布置, 智能的充电蓄能和放电供能, 渗透到了电力系统的发电、输电、配电、用电等各个环节, 其多重运行效益和经济价值日益凸显[2]。同时, 大量的可再生能源的大规模并网, 造成了电网频率的不稳定[3]。储能系统具有快速精确的功率响应能力, 能够提高火电厂的调频能力, 保证电网频率的稳定, 提高电力系统运行的安全性[4]。但储能系统的建设成本比较昂贵, 因此考虑其寿命具有非常重要的意义, 不仅可以对储能系统经济性进行有效评估, 而且也可以对系统的安全运行提供保障。
当前, 我国在电力自动发电控制(Automatic Generation Control, AGC)调频市场化方面已经取得了显著的成效, 实现了AGC的有偿服务和初步的市场竞争[5], 但是目前对储能系统健康度和经济性的研究还有所欠缺。张北风光储输示范项目是国内首个大型将储能系统与风电场联合运行的工程, 该项目尚未取得盈利, 仍处于示范阶段[6]。北京石景山电厂储能调频示范项目的主要研究目的是探索储能系统参与电网调频的盈利方式, 验证储能系统辅助国内火电机组参与调频的可行性。该电厂配备了2 MW的锂离子电池储能调频系统, 调频收益显著增加, 取得了一定的效果[7]。以上项目均验证了储能系统参与电网调频技术上的可行性, 但是由于储能电池的成本较高, 抑制了储能调频技术在我国的大规模应用, 因此有必要对储能系统的健康度和经济性评价进行研究。
电池健康度预测方法主要分为基于经验的方法和基于性能的方法, 但基于电池经验的预测方法往往不够精确, 多数情况下难以满足要求, 故一般采用基于性能的方法来对电池的寿命进行预估。文献[8]针对山西某电厂火电和储能联合调频的工程实际进行了分析, 提出了火电联合储能调频的控制策略, 具有一定的指导意义, 但并没有对储能系统的经济性进行分析。文献[9-10]根据与火电机组具备同等AGC调频能力的储能系统的功率和容量进行了配置, 可满足调频需求, 但并没有根据机组实际运行情况对容量需求和经济性进行分析。
本文首先提出了辅助火电机组参与调频的控制策略和分段调频的控制策略, 然后利用灰色模型算法建立了锂离子电池的循环寿命与电池实际容量之间的容量衰减模型, 实现了对储能系统的健康度预测, 最后分别对两种控制策略下储能系统的经济性进行了分析。
1 储能系统参与火电厂调频的控制策略
在跟随电网AGC调度时, 与传统火电机组相比, 储能系统具有响应速度快、调节精度高、出力较稳定等优点, 但其功率和容量有限, 无法独自承担调峰任务。火电机组响应速度慢、调节精度较低, 但是具有较大的调节范围和容量。基于此, 本文提出了辅助火电机组参与调频的控制策略和分段调频的控制策略。
1.1 辅助火电机组参与调频的控制策略
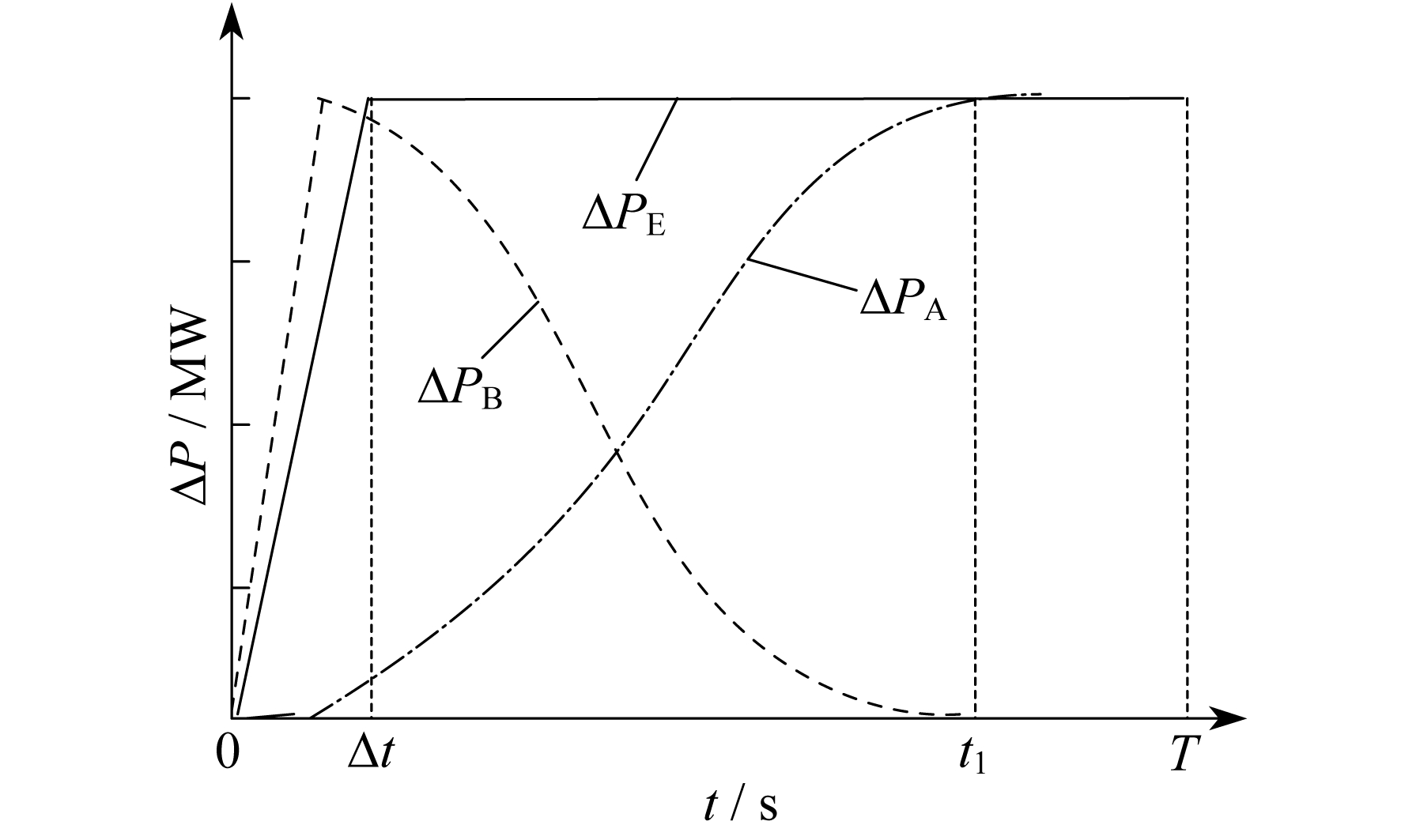
当储能资源参与调频时, 在确定不同时段AGC指令的基准值后, 设机组设定功率指令为ΔPS, AGC的调节功率指令为ΔAGC, 此时响应调频指令以机组出力为主, 储能系统采取对机组出力进行补偿的方式。在一个AGC指令调频周期内, 储能系统和机组的调节过程如图 1所示。图 1中, 机组的出力特性由实测数据辨识所得, ΔP表示调节功率; ΔPA表示机组的调节功率; ΔPB表示储能的调节功率; ΔPE表示储能和机组整体的调节功率。
当AGC调节功率为ΔAGC时, 机组的设定功率ΔPS为
| $\Delta P_{\mathrm{s}}=\Delta A+\Delta P_{\mathrm{I}}$ | (1) |
式中:ΔA——AGC指令功率增量;
ΔPI——一次调频输出功率增量, ΔPI=-KG(KG为发电机的单位调节功率, Δf为频率变化量)。
机组的调节功率为
| $\Delta P_{\mathrm{A}}=G\left(\Delta P_{\mathrm{s}}\right)$ | (2) |
储能系统的调节功率为
ΔPB=k1{ΔPS-G(ΔPS)}, 0≤k1≤1
式中:ΔPB > 0表示储能系统放电, Δ PB < 0表示储能系统充电。
1.2 分段调频的控制策略
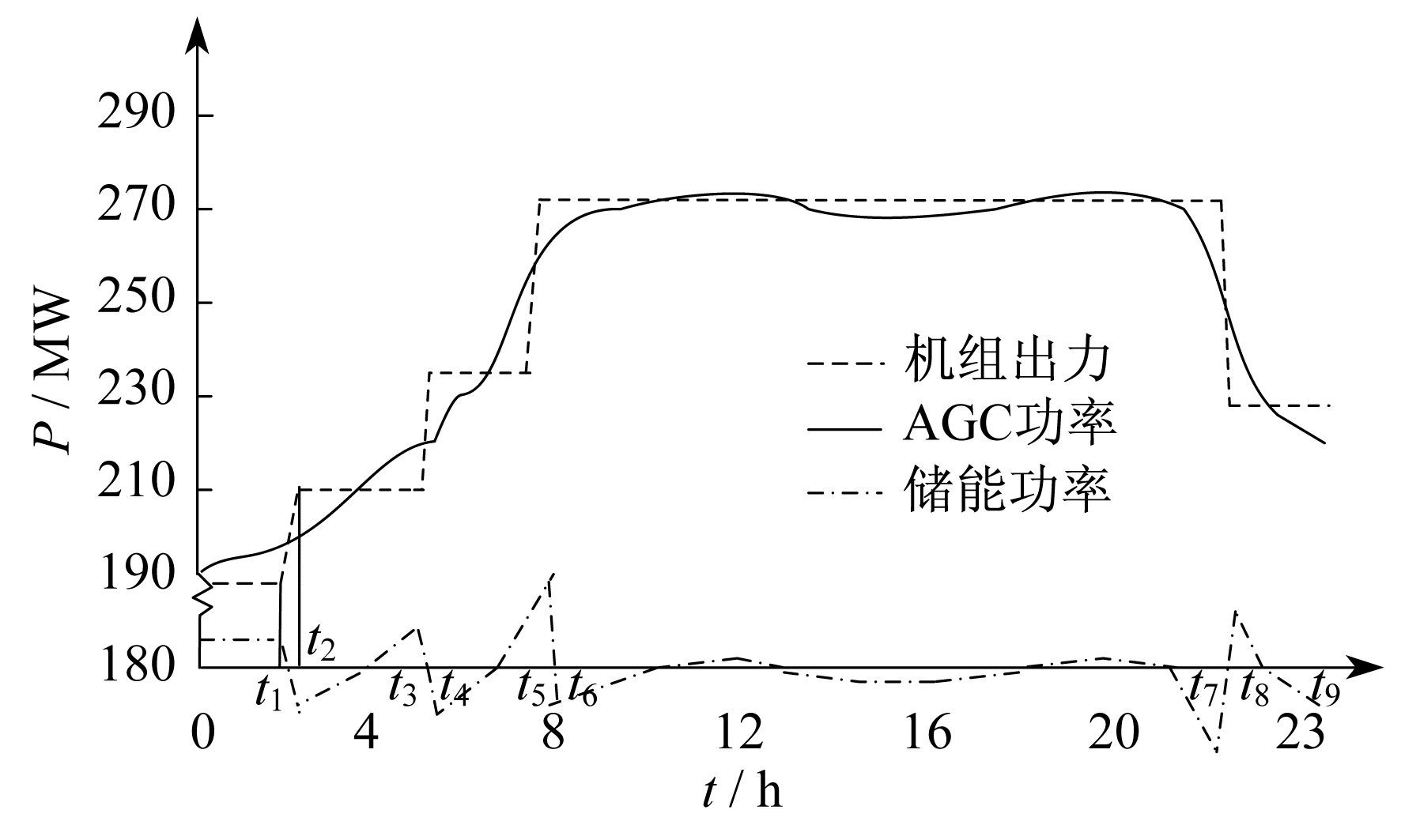
为了避免机组出力变化过于频繁, 减少机组设备的损耗, 同时由于储能系统成本造价昂贵, 单独依赖储能系统又无法满足电网大范围的调频任务, 因此本文采用将机组出力进行分段的方式, 在某一时间段内保持机组出力不变, 储能系统在一定的基准值下进行调频, 储能系统与火电机组联合响应电网的调频指令, 进而形成分段调频的控制策略。分段调节时储能系统和机组出力情况如图 2所示。
图 2中, 机组额定调节速率取0.6PN/h(PN为机组的额定功率)。分段调节时的前提条件是储能系统调频功率小于其额定功率, 否则开始调整机组出力。机组在分段进行调频时, 储能系统对机组的出力进行补偿, 综合响应AGC调频指令。将机组的运行模式分为3种:模式1为机组以恒定功率运行; 模式2为机组匀速爬坡; 模式3为机组匀速下坡。具体如下。
(1) 模式1中, 机组出力保持不变, 设定机组出力PE=Pn(其中n为变量, 表示机组分段的情况), 那么储能系统的出力为PAGC(t)-Pn。在模式1中, 储能的剩余电量(State of Charge, SOC)需满足
| $ \left\{\begin{array}{l} \max \left\{S_{\mathrm{OC}}(t)\right\} \leqslant S_{\mathrm{OC}, \max } \\ \min \left\{S_{\mathrm{OC}}(t)\right\} \geqslant S_{\mathrm{OC}, \min } \end{array}\right. $ |
否则开始进入其他模式。
(2) 模式2中, 机组出力开始匀速增加, 机组出力可以表示为PE= P0+0.6PN(t-t0), 那么储能系统出力为PAGC(t)-P0-0.6PN(t-t0)。其中, PAGC(t)表示AGC指令大小。
(3) 模式3中, 机组出力开始匀速下降, 机组出力可以表示为PE= P′0-0.6PN(t-t0), 那么储能系统出力为PAGC(t)-P′0 +0.6PN(t-t0)。
综上所述, 机组出力的情况可以表示为
| $P_{\mathrm{A}}= \\ \left\{\begin{array}{c}P_{\mathrm{n}} ; S_{\mathrm{OC}, \min } \leqslant S_{\mathrm{OC}}(t) \leqslant S_{\mathrm{OC}, \max } , \\ P_{\mathrm{AGC}}(t)-P_{\mathrm{A}}<P_{\mathrm{B}_{-} \max } \\ P_{0}+0.6 P_{\mathrm{N}}\left(t-t_{0}\right) ; S_{\mathrm{OC}}(t)<S_{\mathrm{OC}, \min } \\ P_{0}^{\prime}-0.6 P_{\mathrm{N}}\left(t-t_{0}^{\prime}\right) ; S_{\mathrm{OC}}(t)>S_{\mathrm{OC}, \max }\end{array}\right.$ | (4) |
2 基于灰色模型算法的储能系统健康度预测及其经济性评价
2.1 基于雨流计数法的循环次数统计方法
本文根据试验获取的电池的退化数据, 建立了锂离子电池的循环寿命与电池实际容量之间的容量衰减模型, 以实现对电池健康度的预测。在储能系统参与调频的过程中, 此模型应用于储能系统的健康度预估时, 首先必须要确定储能电池循环次数, 本文采用雨流计数法来实现对电池循环次数的统计。
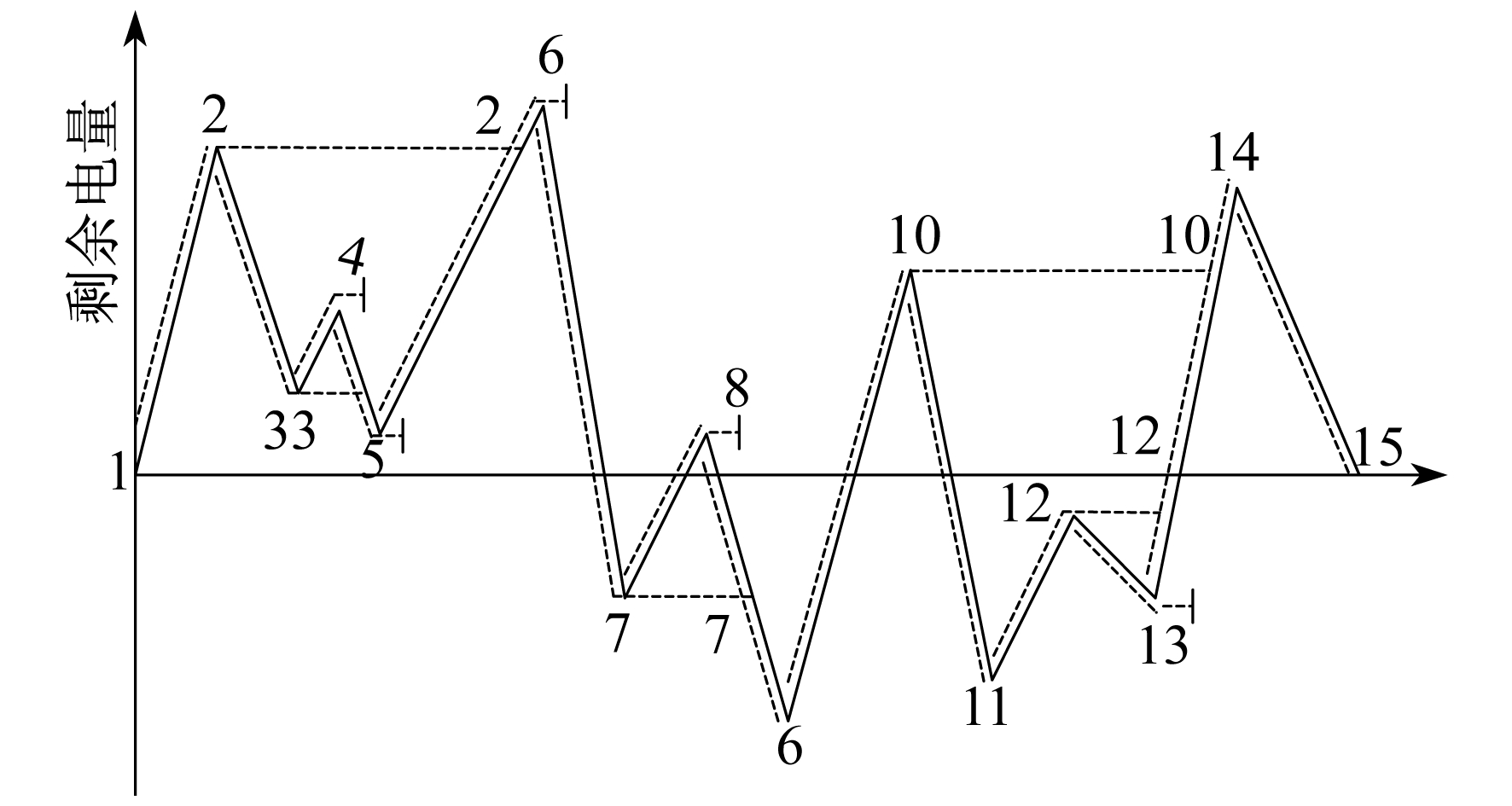
雨流计数法, 又被称作“塔顶法”, 常用于工程中设备的疲劳寿命计算[11]。该方法主要根据研究对象变量之间的非线性关系来计数, 然后确定出样本的非周期性循环次数。在使用的过程中, 储能电池自身电量的SOC值也在来回波动, 因此可以采用雨流计数法对电池的循环次数和放电深度进行计算。雨流计数法原理如图 3所示。
雨流计数法的特点是可以根据研究对象的变量和时间之间的非线性关系进行计数[12]。在储能电池的应用中, 可以根据电池的SOC与时间之间的关系, 统计出样本的循环次数。
雨流计数法的计数规则如下:
(1) 起点从开始记录的点或者各个角的内边开始;
(2) 雨滴在经过角的峰值时开始垂直下落, 直到碰到绝对值比该峰值更大的点或者比该谷值更小的点处;
(3) 雨滴继续流动, 当与上面的雨滴相遇时, 形成一个循环;
(4) 根据雨滴的起点和终点, 将各个循环描绘出来, 然后将所有的循环逐一在图中取出, 记录其峰谷值;
(5) 水流的水平长度值代表了每个循环的幅值, 即该循环周期内电池的放电深度。
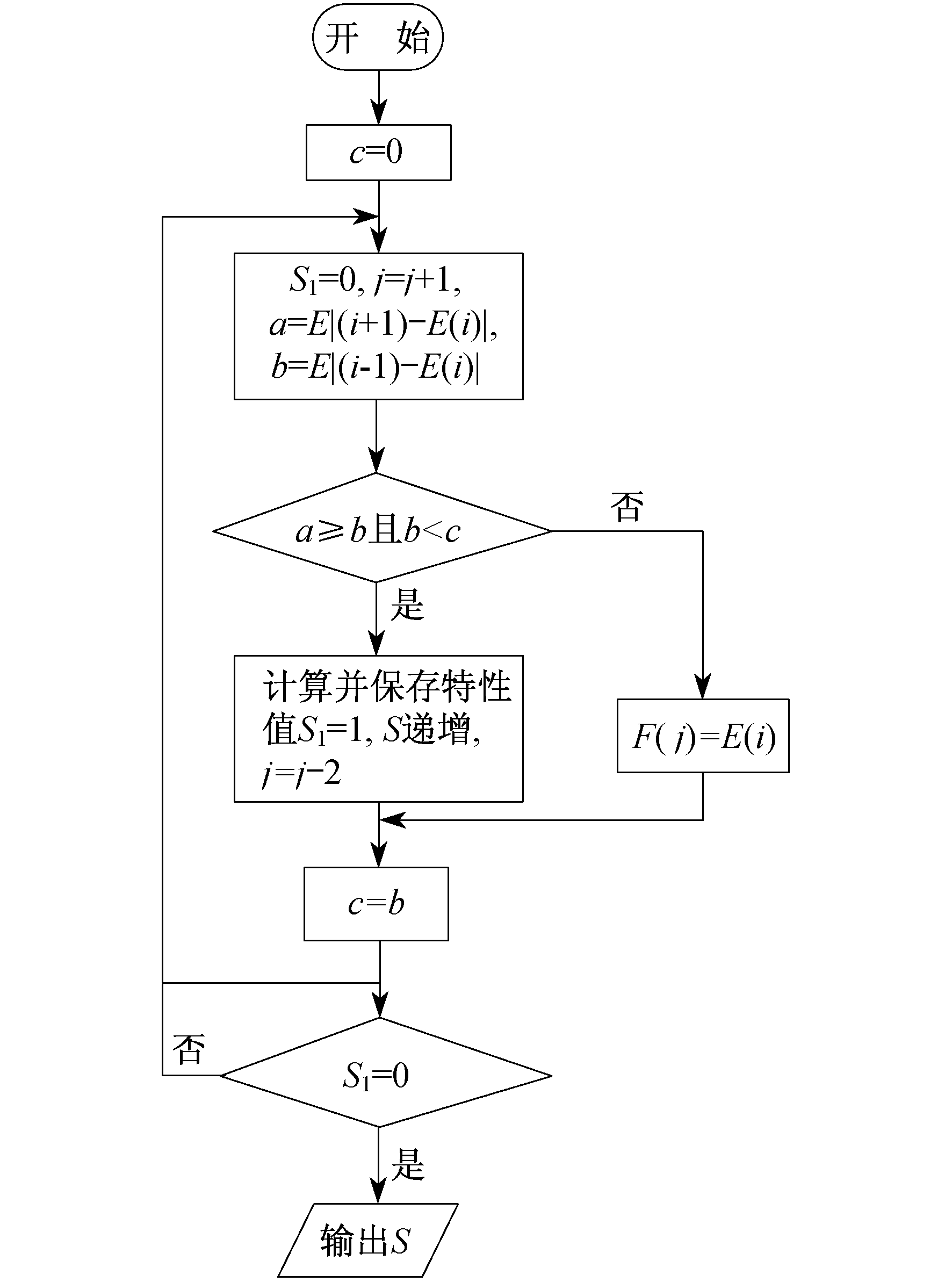
雨流计数法为非线性算法, 其算法的实现步骤主要包括数据压缩和循环数的提取两部分, 本文仅需要通过其获取电池的循环次数。循环判断和循环数提取流程如图 4和图 5所示。
图 5中:E(i)为待处理数据; F(j)为对应的数据压缩处理后的数据; S1表示是否有循环的标志, S1= 0时说明该数组内循环周期已经全部提取出, 否则继续循环过程; S表示提取到的循环周期的总次数。
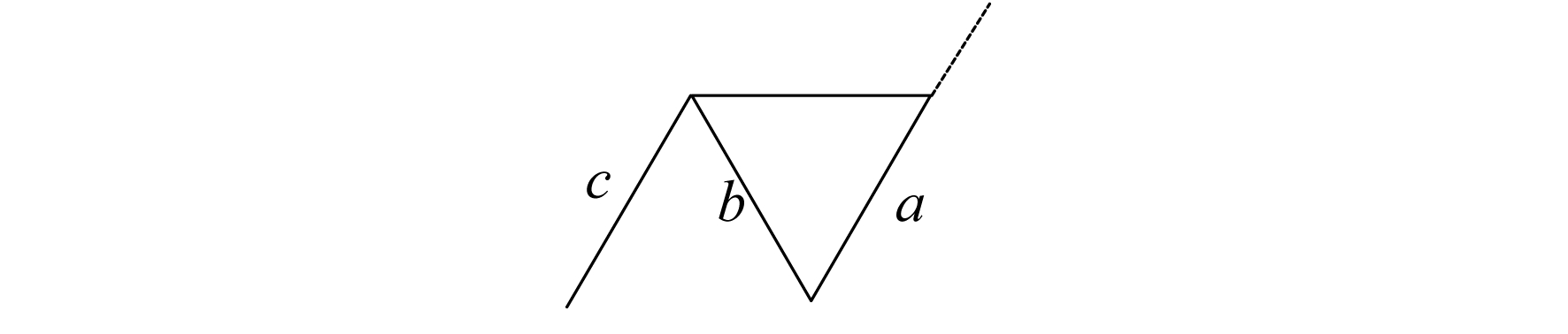
雨流计数法主要从压缩过的处理数据中记录出电池SOC的峰值和谷值, 可以采用四点法对其进行计算[14]。在由电池SOC组成的数组中, 当满足调节a≥b且b < c时, 可以认为构成一个循环, 同时除掉E(i)和E(i-1)两点, 否则记录下E(i)这一点, 然后对数组进行反复判断就能够取出所有的循环。具体实现方法如图 5所示。
假设电池充放电过程中SOC的峰谷值E(i)由E(1), E(2), E(3), …, E(n)组成, 由图 4的循环周期提取流程可得:
当a≥ b且b < c时, 计为一次循环, 设符合条件的次数为n, 那么电池的循环次数为
| $S=n$ | (5) |
其中, a=|E(i+1)-E(i)|, b=|E(i-1)-E(i)|, c=|E(i-1)-E(i-2)|。
当a≥b且b < c时, 满足一个循环条件, 该循环周期内电池的放电深度Dm为
| $D_{m}=E(i+1)-E(i)$ | (6) |
通过雨流计数法对储能系统剩余电量进行统计, 可以确定出储能电池的循环周期和对应循环周期下的放电深度。由于储能电池在充放电的过程中并不是完全放电, 因此需要根据电池的放电深度, 将各个循环周期折算成总的循环次数。设在算法时间段内储能系统的循环周期数为m, 每个循环周期内对应的放电深度为D1, D2, D3, …, Dm, 那么该算法时间段内储能系统总的循环次数X为
| $ X=\sum\limits_{1}^{m} D_{m} $ | (7) |
2.2 基于灰色模型算法的储能系统健康度预测
通常情况下, 将灰色模型定义为GM(n, m), n表示阶数, m表示变量的个数。灰色模型中, 最常见最简单的为一阶灰色模型GM(1, 1), 该模型阶数为1, 含有1个变量。本文采用灰色模型对电池的健康度进行预测, 要点主要包括3个:一是对实验数据的要求, 实验数据不能小于零, 数量要在5个以上, 同时获取数据的时间间隔尽量相同, 绘制出的曲线要有一定的平滑性; 二是认为储能电池的健康度可以用一阶微分方程表示, 并且系数为常数; 三是认为可以建立出储能电池容量的退化模型, 并且模型中的参数是未知的, 需要对参数进行估计[13]。基于灰色模型算法的储能系统健康度的预测主要根据电池容量的量测数据对未知参数进行估计, 然后再利用估计结果对电池的健康度进行预测。
储能电池的灰色模型建立步骤如下[14]。
步骤1 通过对电池的核容放电试验, 得到储能电池容量的原始数据
| $Q_{i}=\left\{Q_{i}, i=1,2,3, \cdots, N\right\}$ | (8) |
步骤2 为了减少原始测量数据的误差, 需要对原始数据进行累加处理, 得到电池容量数据的累加值为
| $ Q_{i}^{(1)}(k)=\sum\limits_{i=1}^{k} Q_{i}, i=1,2,3, \cdots, k $ | (9) |
然后进一步生成电池容量数据的累加值序列向量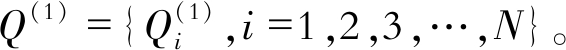
步骤3 建立灰色模型, 完成对未知参数的估计。
设基于电池容量的一阶灰色模型为
| $ \frac{\mathrm{d} Q_{t}^{(1)}}{\mathrm{d} t}+a Q_{t}^{(1)}=b $ | (10) |
式中:a——灰色模型的发展系数;
b——灰色作用量。
设GM(1, 1)模型的背景值为
| $ y(k)=\frac{1}{2}\left(Q_{k}^{(1)}+Q_{k-1}^{(1)}\right), k=1,2,3, \cdots, N $ | (11) |
那么对于灰色模型GM(1, 1), 有如下方程
| $B_{N} \alpha=Y_{N}$ | (12) |
其中,

然后借助最小二乘法, 可以求出待估计参数的值为
| $ \hat{\alpha}_{N}=\left[\begin{array}{c} \hat{a}_{N} \\ \hat{b}_{N} \end{array}\right]=-\left(B_{N}^{\mathrm{T}} B_{N}\right)^{-1} B_{N}^{\mathrm{T}} Y_{N} $ | (13) |
步骤4 对一阶灰色模型进行求解, 即求微分方程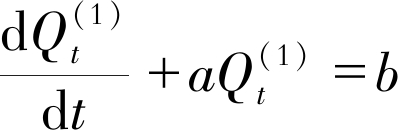 的解。
的解。
| $ Q_{t}^{(1)}=\left(Q_{0}^{(1)}-\frac{b}{a}\right) \exp (-a t+a)+\frac{b}{a} $ | (14) |
可以得到Qk的表达式为
| $ \begin{aligned} Q_{k+1}=& Q_{k+1}^{(1)}-Q_{k}^{(1)}=\left(Q_{0}^{(1)}-\frac{b}{a}\right) \cdot \\ \exp (-a k)(\exp (-a)-1) \end{aligned} $ | (15) |
式中:取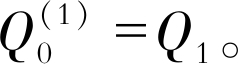
步骤5 利用灰色模型对电池健康度进行预测, 建立电池容量预测模型为
| $ \begin{aligned} \hat{Q}_{N+p}=& \left(Q_{0}^{(1)}-\frac{b_{N}}{\hat{a}_{N}}\right) \exp \left[-\hat{a}_{N}(N+p)\right] \cdot \\ & \left[\exp \left(-\hat{a}_{N}\right)-1\right] \end{aligned} $ | (16) |
式中:
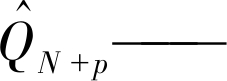 第p次循环后电池的容量;
第p次循环后电池的容量;
| $ Q_{0}^{(1)}=Q_{1} $ |
由最终得到的电池容量预测模型, 即式(16)可以实时估计出电池的实际容量。当预测值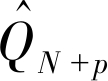 衰减到0.8 QN时, 认为电池的寿命终止。
衰减到0.8 QN时, 认为电池的寿命终止。
2.3 一体化调频系统的经济性评价
由于储能系统造价比较昂贵, 因此在利用其参与电网调频时, 有必要展开对一体化调频系统的经济性评价。首先对一体化调频系统的成本和收益展开分析, 然后通过对投资回报率的计算实现对储能系统的经济性分析。
锂离子电池的充放电效率较高, 可以达95%以上[15], 因此本文在计算电池储能系统成本时可以忽略能量损耗带来的成本。电池储能系统的成本主要由初试投资成本和运行维护成本组成, 其中占比最大的是电池的初始投资成本。
2.3.1 初始投资成本
一体化调频系统的投资成本主要由功率建设成本和容量建设成本组成。功率成本主要包括逆变器及相应配套设备的成本, 容量成本指的是锂离子电池的购买成本。
电池的初始投资成本主要包括电池成本、逆变器及相应配套设备的成本。初始投资成本C1表达式为
| $C_{1}=K_{1} Q_{\mathrm{NN}}+K_{2} P_{\mathrm{NN}}$ | (17) |
式中:K1——电池单位容量的成本;
QNN——电池的额定容量;
K2——逆变器及配套设备的成本;
PNN——储能系统的额定功率。
2.3.2 运行维护成本
一体化调频系统的运行维护成本指的是维持调频系统处于正常的工作状态以及保证良好和安全的工作环境所需要花费的成本。
在计算运行维护成本时, 暂时不考虑更换设备带来的费用。储能系统的运行维护成本C2主要与储能系统的容量有关系, 可以表示为
| $C_{2}=K_{3} Q_{\mathrm{NN}}$ | (18) |
式中:K3——储能系统的运行维护单价。
储能系统总成本的表达式为
| $C=K_{1} Q_{\mathrm{NN}}+K_{2} P_{\mathrm{N}}+K_{3} Q_{\mathrm{NN}}$ | (19) |
2.3.3 调频补偿收益
由文献[16]可得储能系统和机组一体化系统参与AGC的按调节深度进行补偿的公式为
| $ R_{1}=\sum\limits_{i=1}^{n} D_{i} Y_{2} K_{\mathrm{p} 2} $ | (20) |
式中:Di——补偿深度;
Y2——AGC补偿标准, 火电机组取5元/MW;
Kp2——机组当天的调节性能指标。
在计算一体化调频系统带来的收益时, 由于其他间接收益暂时无法具体计算, 因此可以只计算带来的直接收益, 即调频补偿收益和黑启动带来的收益。其表达式为
| $ R=\sum\limits_{i=1}^{n} D_{i} Y_{2} K_{\mathrm{p} 2}+\sum\limits_{i=1}^{k} t_{i} Y_{\mathrm{B}} $ | (21) |
式中:t——参与黑启动的时间;
YB——每天补偿的标准金额。
那么储能系统的投资回报率计算公式可以表示为
| $H=\frac{\sum\limits_{i=1}^{n} D_{i} Y_{2} K_{\mathrm{p} 2}+\sum\limits_{i=1}^{k} t_{i} Y_{\mathrm{B}}}{K_{1} Q_{\mathrm{NN}}+K_{2} P_{\mathrm{NN}}+K_{3} Q_{\mathrm{NN}}} \times 100 \%$ | (22) |
3 算例分析
3.1 储能电池寿命预测分析
在20 ℃下对某型号磷酸铁锂电池进行加速循环试验(充电至14.6 V, 连续放电至10.8 V, 均为2C倍率), 对电池进行放电试验, 通过2 100次的循环试验得到电池容量与循环次数的试验数据如表 1所示。
表 1
在20 ℃和2C倍率下锂电池循环试验数据
| 循环次数 | 电池容量 | 循环次数 | 电池容量 |
| 1 | 0.99 | 1200 | 0.94 |
| 300 | 0.98 | 1500 | 0.93 |
| 600 | 0.97 | 1800 | 0.91 |
| 900 | 0.96 | 2100 | 0.89 |
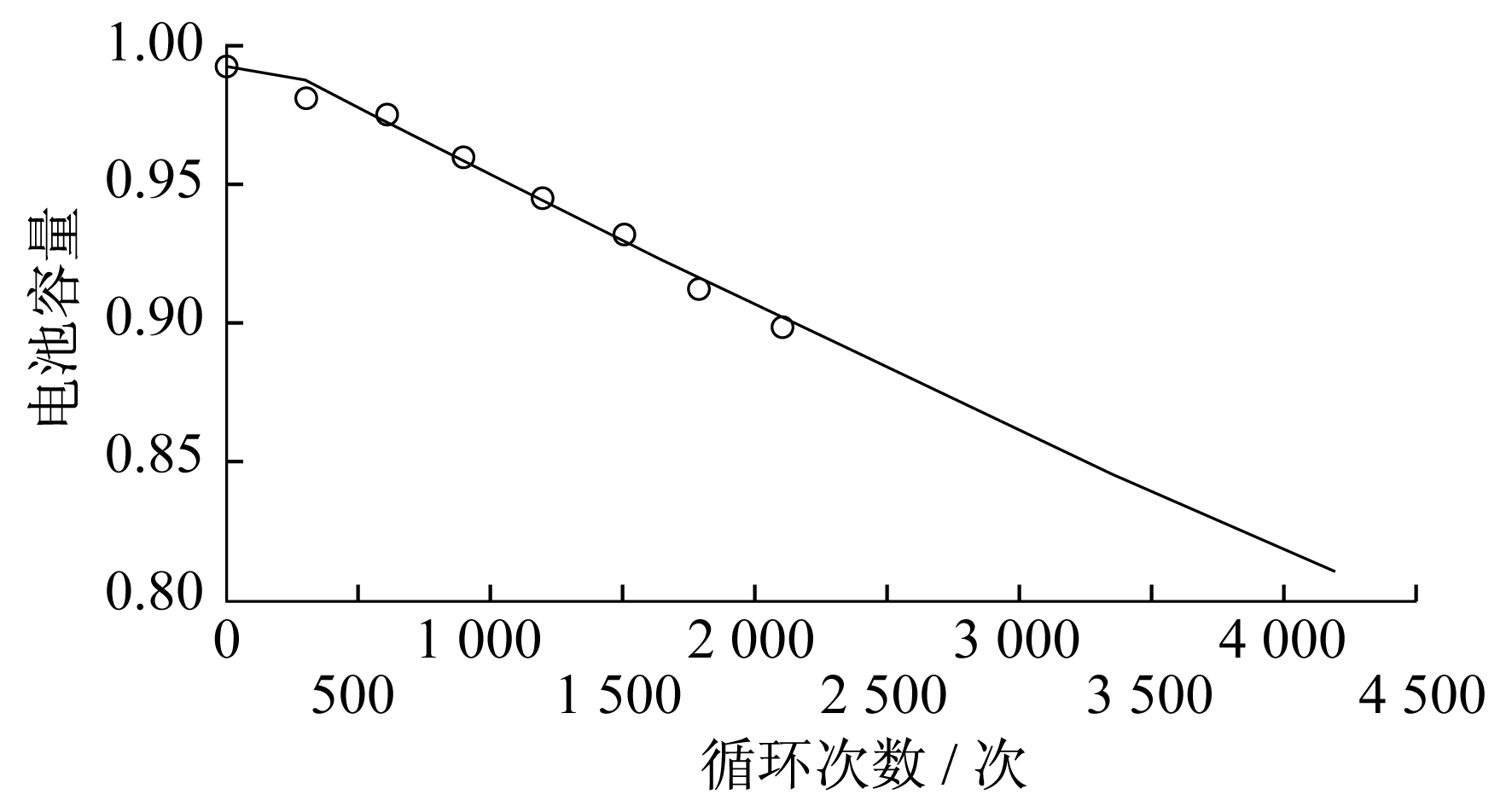
利用试验数据, 建立电池实际容量和循环次数的GM(1, 1)模型, 同时借助MATLAB平台, 得到基于灰色模型的电池容量的预测结果如图 6所示。
得到的预测模型为
| $ Q_{k+1}^{(1)}=(0.993-66.8) \mathrm{e}^{-0.015(k-1)}+66.8 $ | (23) |
式中:
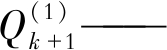 第k次循环后电池的容量。
第k次循环后电池的容量。
由图 6可知, 电池容量衰减较为缓慢, 曲线接近一次函数模型, 前2 100次拟合有较高的精度, 2 100次以后为预测部分。
灰色模型比较适用于电池容量衰减特性基本保持不变的情况。如果电池容量开始衰减缓慢, 而后电池容量迅速退化, 采用灰色模型法可能会有较大误差。由图 6可以看出, 灰色模型算法比较适用于电池寿命的短期预测, 可以取得较好的效果。
3.2 储能系统投资回报分析
对内蒙古某电厂容量为300 MW的机组进行储能系统配置的研究。以2016年8月该机组接收到的AGC指令数据为例, 分别对两种控制策略下该机组的调频效果以及投资回报进行分析。
计算所需参数均参考行业标准[16]:锂离子电池储能系统单位投资成本2 000元/kWh, 储能系统的功率单价为1 000元/kW, 运行维护成本每天0.05元/kWh, 一体化调频系统标准响应时间为10 s。根据文献[16-17]的规定, 确定各指标参数如下:机组标准调节速率为0.01PN; 机组标准调节精度为0.01Pn; 机组标准响应时间为15 s; AGC调频效果补偿标准为5元/MW, 黑启动收益补偿标准为6 000元/天。
采用两种控制策略, 利用式(22)进一步计算, 得到经济性对比结果如表 2所示。
表 2
两种控制策略下储能系统的经济性分析
| 控制 策略 |
功率/ MW |
容量/ MWh |
Kp | 年收益 | 成本 | 每年 投资 回报 率/% |
| 万元 | ||||||
| 1 | 3 | 0.92 | 5 | 306 | 651 | 51 |
| 2 | 20 | 21.50 | 48 | 2 886 | 7 055 | 41 |
当采用第1种控制策略, 即配置额定功率为3 MW、电池容量为0.92 MWh的储能系统时, 通过对AGC指令和机组实际运行数据分析可知, 该工作日储能系大约需要充放电循环约15次, 预计电池的寿命约为1.25年。以年为计算单位, 一体化调频系统总投资651万元, 可以带来的收益约为306万元, 该策略下预计3年左右可以收回成本, 投资回报率约为51%。但是该电池使用寿命达不到3年, 因此在电池选型时需要选择高性能的磷酸铁锂电池, 需要具有很高的循环寿命才能保证储能系统的经济性。
当采用第2种控制策略, 即配置功率为20 MW、电池容量为21.50 MWh的储能系统时, 通过对AGC指令和机组实际分段情况可知, 该工作日储能系统需要充放电循环约6次, 预计电池的寿命约为2.5年。以年为计算单位, 一体化调频系统总投资7 055万元, 每年可以带来的收益约为2 886万元, 预计3年左右可以收回成本, 投资回报率约为41%。但是该电池使用寿命也达不到3年, 因此在电池选型时, 同样需要选择高性能的磷酸铁锂电池, 具有很高的循环寿命才能保证储能系统的经济性。
通过对两种控制策略和对应容量配置方法的经济性分析可知, 第1种控制策略总投资较少, 第2种控制策略对储能系统的功率和容量需求更大, 因此投资成本较大。第1种控制策略下的投资回报率大于第2种控制策略下的投资回报率。在采用高性能保证储能系统寿命的情况下, 第1种控制策略在经济性方面更好。采用第1种控制策略, 不改变机组原有的控制逻辑, 储能系统的出力对机组没有影响, 即使储能系统出现故障, 火电机组依旧可以正常参与电网调频, 因此安全性也更高一些。
4 结语
本文主要对储能系统应用于火电厂调频的健康度及经济性进行了研究, 提出了辅助火电机组参与调频的控制策略和分段调频的控制策略。通过试验获取电池的退化数据, 建立电池健康度的预测模型, 同时利用雨流计数法对电池循环次数进行统计, 以实现对电池健康度的预测。在此基础上, 基于文中提出的控制策略和电池健康度预测方法对储能系统参与电厂调频的经济性展开评价, 计算得出其投资回报率。结果表明, 必须选择高性能的电池才能满足一体化调频系统经济性要求, 否则电池寿命较短, 经济性较差。在采用高性能电池保证储能系统寿命的情况下, 第1种控制策略下的投资回报率更高, 而且该控制策略有着较高的安全性, 因此更适合与火电机组进行联合调频。
参考文献
-
[1]浅谈电力储能技术及其在现代电力系统中的应用[J]. 电子世界, 2014(7): 276.
-
[2]储能技术在电力系统中的应用分析[J]. 电力建设, 2016, 37(8): 24-30. DOI:10.3969/j.issn.1000-7229.2016.08.004
-
[3]BEVRANI H, GHOSH A, LEDWICH G. Renewable energy sources and frequency regulation: survey and newperspectives[J]. let Renewable Power Generation, 2010, 4(5): 438-457. DOI:10.1049/iet-rpg.2009.0049
-
[4]常建平, 陈大宇.储能参与调频服务在我国的发展构想[EB/OL]. (2012-11-09)[2019-01-22].https://wenku.baidu.com/view/8b2201f8f90f76c660371a07.html.
-
[5]并网电厂管理考核系统中AGC调节性能补偿措施[J]. 电力系统自动化, 2010, 34(4): 107-111.
-
[6]大规模储能电源参与电网调频研究综述[J]. 电力系统保护与控制, 2016, 44(7): 145-153.
-
[7]储能技术的发展现状与展望[J]. 吉林水利, 2018, 10(2): 58-62.
-
[8]火电联合储能调频技术的研究与应用[J]. 山西电力, 2017(6): 62-66. DOI:10.3969/j.issn.1671-0320.2017.06.018
-
[9]辅助火电机组参与电网调频的BESS容量配置[J]. 储能科学与技术, 2014, 3(4): 302-307. DOI:10.3969/j.issn.2095-4239.2014.04.002
-
[10]储能调频系统控制策略与投资收益评估研究[J]. 现代电力, 2012, 33(1): 80-86.
-
[11]脉冲负载条件下基于雨流计数法的储能电池寿命预测[J]. 技术与方法, 2017, 36(16): 84-88.
-
[12]雨流计数法及其在程序中的具体实现[J]. 计算机技术与应用, 2004, 24(3): 38-40.
-
[13]EINHORN M, ROESSLER W, FLEIG J. Improved performance of serially connected Li-Ionbatteries with active cell balancing in electric vehicles[J]. IEEE Transactions on Vehicular Technology, 2011, 60(6): 2448-2457. DOI:10.1109/TVT.2011.2153886
-
[14]WAI R J, TU C H. Adaptive grey control for hybrid resonant driving linear piezoelectric ceramic motor[J]. IEEE Transactions on Industrial Electronics, 2006, 53(6): 640-656.
-
[15]规模储能装置经济效益的判据[J]. 电池, 2011, 41(1): 19-21. DOI:10.3969/j.issn.1001-1579.2011.01.007
-
[16]华北电监局.华北区域并网发电厂辅助服务管理实施细则(试行)[EB/OL]. (2018-06-04)[2019-02-08]. http://guangfu.bjx.com.cn/news/20180604/902947.shtml.
-
[17]华北电监局.华北区域发电厂并网运行管理实施细则(试行)[EB/OL]. (2018-06-04)[2019-02-08]. http://guangfu.bjx.com.cn/news/20180604/902947.shtml.