|
|
|
发布时间: 2019-10-10 |
|
|
|
|
收稿日期: 2019-04-02
基金项目: 上海市电站自动化技术重点实验室资助项目(13DZ2273800);国家自然科学基金(61273190)
中图法分类号: TM731;TM732
文献标识码: A
文章编号: 1006-4729(2019)05-0486-07
|
摘要
基于能源互联网理念的提出和可再生能源的快速发展, 计及储能装置的运行特性, 考虑冷电联供的经济性, 兼顾系统的环保性和节能性, 以综合成本为目标, 搭建了含风电、光电等多种可再生能源和冷储能装置的冷电联供系统优化调度模型。基于对冷负荷需求和风电、光电出力的日前预测, 采用自适应布谷鸟算法求解模型, 得到不同运行方案下各机组的最佳调度方案。通过算例仿真发现, 含有多种可再生能源和冷储能装置的冷电联供系统可以充分发挥可再生能源发电特有的经济、环保优势, 减少了一次能源的消耗。仿真结果验证了模型的有效性。
关键词
可再生能源; 储能; 冷电联供; 经济调度
Abstract
Based on the concept of energy Internet and the rapid development of renewable energy, taking into account the operating characteristics of energy storage devices, an optimized scheduling model for cogeneration systems including wind power, photovoltaics and other renewable energy and cold energy storage devices was built, considering the economy cooling and power-supply, taking into account environmental protection and energy efficiency of the system, the overall cost as the goal.Based on the cooling load demand and the wind power and photoelectric output prediction, the adaptive cuckoo algorithm is used to build the model, and the optimal scheduling schemes for each unit under different operation schemes is obtained.Through the simulation of the example, the quantitative analysis of the cogeneration system containing multiple renewable energy sources and cooling energy storage devices can sufficiently utilize its special economic, environmental advantages, reducing the consumption of primary energy.The validity of the model is verified.
Key words
renewable energy; energy storage; cold electricity cogeneration; economic dispatching
随着能源危机和环境污染问题的加重, 可再生能源的发展和能源结构的优化成为热门的研究课题。冷电联供(Combined Cooling and Power, CCP)系统以其节能、环保的优势越来越受到人们的关注[1]。CCP系统集成了冷能、电能、天然气等多种能源形式, 在发电的同时对系统产生的废热进行回收制冷, 对能源进行梯级利用, 达到了节能减排的效果[2-3]。随着能源互联网理念的提出, 将可再生能源、电能、冷能和天然气等能源相结合组成新的能源利用体系, 提高可再生能源的渗透率, 推动能源结构的改革[4-5], 从根本上缓解能源危机和环境污染问题, 对未来的冷电联供系统优化研究具有重要意义。
目前, CCP系统经济优化调度是冷电联供系统优化研究的重要方面, 专家学者们也取得了一些研究成果。文献[6]考虑到储热装置的影响, 搭建了含储热装置的风热电联合优化模型, 并验证了模型的有效性和经济性。文献[7]将电转气技术和有机朗肯循环系统与热电联产相结合, 实现了热电解耦和区域能源系统的经济运行。文献[8]在热电联产系统中引入氢气-燃料电池储能技术, 实现了热、电存储一体化, 提高了能源系统的经济性, 但储电效率低且价格昂贵, 未能应用于实际生产。文献[9]针对微电网中风电的不确定性, 建立了热电联供型微电网双层鲁棒优化调度模型, 引入了线性优化强对偶理论, 并结合Big-M法和列约束生成算法进行求解, 采用电锅炉协调供热, 增加了风电的消纳空间。但以上研究大多是针对热电联供系统的优化, 且未考虑接入多种可再生能源, 实现能源的高效综合利用。
针对上述分析, 本文采用太阳能、风能、电能、地热能和天然气等多能源互补供能方式, 建立了含多种可再生能源和冷储能装置的冷电联供优化调度模型。综合系统的经济性、环保性和节能性, 构建了以综合成本最小为目标函数的模型, 并采用自适应布谷鸟算法进行求解, 得到了各机组的最优调度方案。最后, 以传统的冷电联供调度模型作为对比方案, 验证了本文模型的经济性和环保性。
1 CCP系统结构
1.1 CCP系统各单元的数学模型
1.1.1 微型燃机
微型燃机的余热排放量和发电效率的数学模型分别为
| $ Q_{\mathrm{mt}}(t)=\frac{P_{\mathrm{mt}}(t)\left(1-\eta_{\mathrm{mt}}-\beta\right)}{\eta_{\mathrm{mt}}} $ | (1) |
| $ \begin{aligned} \eta_\mathrm{m t}=& 0.0753\left[\frac{P_{\mathrm{m t}}(t)}{65}\right]^{3}-0.3095\left[\frac{P_{\mathrm{m t}}(t)}{65}\right]^{2}+\\ & 0.4174\left[\frac{P_{\mathrm{m t}}(t)}{65}\right]+0.1068 \end{aligned} $ | (2) |
式中:Qmt(t)——t时段微型燃机的余热排放量;
Pmt(t)——t时段微型燃机的发电功率;
ηmt——微型燃机的发电效率;
β——微型燃机的散热损失系数。
1.1.2 溴冷机
溴冷机可利用的余热量以及制冷量的数学模型为[11]
| $ \left\{\begin{array}{l} Q_{\mathrm{re}}(t)=\eta_{\mathrm{re}} Q_{\mathrm{mt}}(t) \\ Q_{\mathrm{rec}}(t)=\alpha_{\mathrm{c}} Q_{\mathrm{re}}(t) \end{array}\right. $ | (3) |
式中:Qre(t)——t时段溴冷机可利用的余热量;
ηre——微型燃机的烟气余热回收率;
Qrec(t)——t时段溴冷机的制冷量;
αc——溴冷机的制冷系数。
1.1.3 地源热泵
1.1.4 冷储能装置
冷储能装置可以有效缓解CCP系统和用户间的能量供需不平衡, 减少装机容量, 提高系统的运行效率和供能稳定性[14]。水蓄能因其技术要求低、维修方便等优点在CPP系统优化运行中获得了广泛应用。水蓄冷储能装置的数学模型为
| $Q_{\mathrm{rc}}(t)=(1-\tau) Q_{\mathrm{rc}}(t-1)+Q_{\mathrm{sc}}(t) \eta_{\mathrm{ch}}$ | (5) |
| $Q_{\mathrm{rc}}(t)=(1-\tau) Q_{\mathrm{rc}}(t-1)+\frac{Q_{\mathrm{sc}}(t)}{\eta_{\mathrm{dis}}}$ | (6) |
式中:Qrc(t)——t时段冷储能装置的剩余冷能;
τ——冷储能的损失系数;
Qsc(t)——t时段冷储能装置的冷能输入(输出)量, 值为正时表示输入量, 值为负时表示输出量;
ηch, ηdis——冷储能装置的能量输入、输出转换效率。
1.2 目标函数
本文综合考虑系统的经济性、环保性和节能性等多个评价指标, 在满足冷、电负荷需求的前提下, 对天然气和电能进行合理利用, 实现综合费用最小化, 以达到整个系统的优化运行。CCP系统的综合费用模型为
| $ \begin{aligned} F=& \sum_{t=1}^{T}\left[f_{\mathrm{FU}}(t)+f_{\mathrm{OM}}(t)+f_{\mathrm{EX}}(t)+\right.\\ & \left.f_{\mathrm{EN}}(t)-f_{\mathrm{CH}}(t)\right] \end{aligned} $ | (7) |
| $ \left\{\begin{aligned} f_{\mathrm{FU}}(t)=& C_{\mathrm{FU}} \frac{P_{\mathrm{mt}}(t)}{\eta_{\mathrm{mt}}} \frac{\Delta t}{L_{\mathrm{FU}}} \\ f_{\mathrm{OM}}(t)=& k_{\mathrm{mt}} P_{\mathrm{mt}}(t) \Delta t+k_{k} \sum_{k=1}^{m} P_{k}(t) \Delta t+\\ & k_{s}\left|P_{\mathrm{sc}}(t)\right| \Delta t \\ f_{\mathrm{EX}}(t)=& C_{\mathrm{rb}}(t) \max \left\{P_{\mathrm{EX}}(t), 0\right\}+\\ & C_{\mathrm{rs}}(t)\left\{-P_{\mathrm{EX}}(t), 0\right\} \\ f_{\mathrm{EN}}(t)=& \alpha\left[\mu_{\mathrm{e}} P_{\mathrm{EX}}(t)+\mu_{\mathrm{f}} \frac{P_{\mathrm{mt}}(t)}{\eta_{\mathrm{mt}} L_{\mathrm{FU}}}\right] \\ f_{\mathrm{CH}}(t)=C_{\mathrm{c}} \mathrm{Q}_{\mathrm{c}}(t) \end{aligned}\right. $ | (8) |
式中:fFU(t)——t时段系统购买能源的成本;
fOM(t)——t时段机组的维护成本;
fEX(t)——t时段大电网的交互成本;
fEN(t)——t时段系统排放CO2产生的环境成本;
fCH(t)——t时段系统的供冷收益;
T——调度周期;
CFU——能源价格, 本文中天然气的价格为2.5元/m3;
LFU——低热值, 为9.7 kWh/m3;
kmt, kk, ks——微型燃机、第k种可再生能源以及冷储能装置单位电能的维护费用;
Pk(t)——t时段第k种可再生能源的输出功率;
Psc(t)——冷储能装置的冷能输入(输出)功率, Psc(t) > 0时为输入功率, Psc(t) < 0时为输出功率;
Crb(t), Crs(t), Cc——t时段的购电、售电及供冷单价;
α——治理CO2气体的单位成本;
μe, μf——电网燃煤和微型燃机消耗天然气发电过程中CO2的排放系数;
PEX(t), Qc(t)——t时段与电网交易的电功率及冷负荷需求。
1.3 系统约束条件
1.3.1 等式约束
等式约束主要包含冷、电功率平衡约束和冷储能设备调度周期内始末冷能储存量约束, 公式为
| $P_{\mathrm{mt}}(t)+\sum\limits_{k=1}^{m} P_{k}(t)+P_{\mathrm{EX}}(t)=P_{\mathrm{L}}(t)+P_{\mathrm{hp}}(t)$ | (9) |
| $Q_{\mathrm{rec}}(t)+Q_{\mathrm{hpc}}(t)+Q_{\mathrm{sc}}(t)=Q_{\mathrm{c}}(t)$ | (10) |
| $Q_{\mathrm{rc}}(0)=Q_{\mathrm{rc}}(t)$ | (11) |
式中:PL(t)——电负荷需求;
m——可再生能源的数目。
1.3.2 不等式约束
与电网交互约束条件为
| $\min P_{\mathrm{EX}}(t) \leqslant P_{\mathrm{EX}}(t) \leqslant \max P_{\mathrm{EX}}(t)$ | (12) |
机组出力约束条件为
| $\min P_{\mathrm{mt}}(t) \leqslant P_{\mathrm{mt}}(t) \leqslant \max P_{\mathrm{mt}}(t)$ | (13) |
| $\min P_{\mathrm{hp}}(t) \leqslant P_{\mathrm{hp}}(t) \leqslant \max P_{\mathrm{hp}}(t)$ | (14) |
冷储能设备的运行特性约束条件为
| $ \left\{\begin{array}{l} -P_{\mathrm{sc}, \max }(t) \leqslant P_{\mathrm{sc}}(t) \leqslant P_{\mathrm{sc}, \max }(t) \\ \mu_{\min } C_{\mathrm{sc}}(t) \leqslant C_{\mathrm{sc}}(t) \leqslant \mu_{\max } C_{\mathrm{sc}}(t) \\ \lambda_{\mathrm{in}}(t)+\lambda_{\mathrm{out}}(t) \leqslant 1 \end{array}\right. $ | (15) |
式中:Psc, max(t)——冷储能装置的最大输入功率;
μmin, μmax——冷储能装置的最小、最大荷电状态;
Csc——冷储能装置的容量;
λin(t), λout(t)——t时段冷储能设备工作状态的0-1变量。
其中, λin(t)=1表示冷储能设备工作在储冷状态, λout(t)=1表示冷储能设备工作在释冷状态。
2 求解算法及调度策略
本文建立的冷电联供优化调度模型本质上为带约束条件的混合整数非线性规划问题, 可以描述为
| $ \left\{\begin{array}{l} \min f(x, y), x \in R^{n}, y \in\{0,1\} \\ \text { s.t. } \quad g_{i}(x, y)=0, i=1,2,3, \cdots, N \\ q_{j}(x, y) \leqslant 0, j=1,2,3, \cdots, M \end{array}\right. $ | (16) |
式中:f(x, y)——目标函数;
x——n维优化变量, 包括微型燃机的出力、可再生能源机组的出力、与大电网的交互情况、储能设备的输入输出功率以及地源热泵消耗的电功率等;
y——冷储能设备的工作状态。
其中, gi(x, y)=0表示i个等式约束函数, qj(x, y)≤0表示j个不等式约束函数。
2.1 自适应布谷鸟算法
冷电联供系统在优化调度的过程中需要求出的解变量包括各时段的微型燃机的出力、可再生能源机组的出力、与大电网的交互情况、储能设备的输入输出功率, 以及地源热泵消耗的电功率等。在基本的布谷鸟算法中, 莱维飞行的随机步长S对算法的全局搜索能力和收敛速度非常重要。S越大, 越容易快速接近全局最优解, 但不能保证收敛精度; 反之, 提高寻优精度, 则会降低收敛速度。基于上述问题, 本文采用引入自适应步长的布谷鸟算法进行求解[15], 相关的计算公式为
| $ d_{i}=\frac{\left\|x_{i}-x_{\mathrm{b}}\right\|}{d_{\max }} $ | (17) |
| $S_{i}=S_{\min }+d_{i}\left(S_{\max }-S_{\min }\right)$ | (18) |
式中:xi——鸟巢i当前的位置;
xb——当前记录的鸟巢的最优位置;
dmax——鸟巢的最优位置与其他鸟巢位置的最远距离;
Smax, Smin——步长调整因子的最大值和最小值。
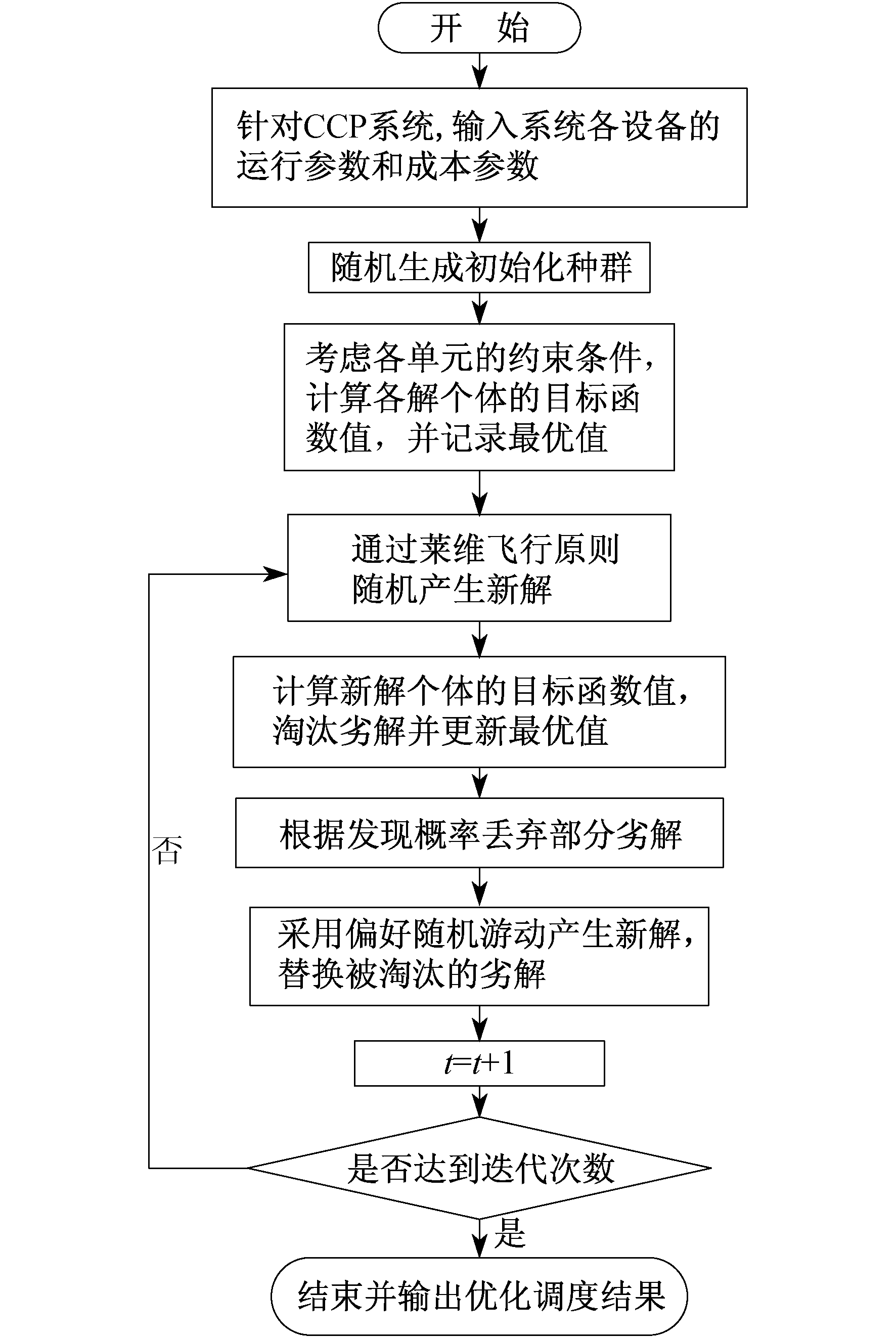
自适应布谷鸟算法的具体求解流程如图 2所示。
2.2 调度策略
针对优化调度问题, 采用如下调度策略结合自适应布谷鸟算法, 共同对CCP系统模型进行求解, 从而确定各机组的负荷分配情况。
(1) PV和WT属于可再生能源机组, 不会产生能源成本, 也不会排放CO2, 只需考虑机组维护成本, 因此优先利用风电和光电, 并采取最大功率输出模式的策略。
(2) 用户的电负荷需求主要由PV, WT, MT产生的电能供应, 不足的电负荷需求根据当前时段发电成本的高低选择MT发电或者向电网进行购买, 多余的电量可输向电网获取利益。
(3) 冷负荷需求由MT配合溴冷机、HP和CS共同进行供应。
3 算例分析
3.1 算例基础数据
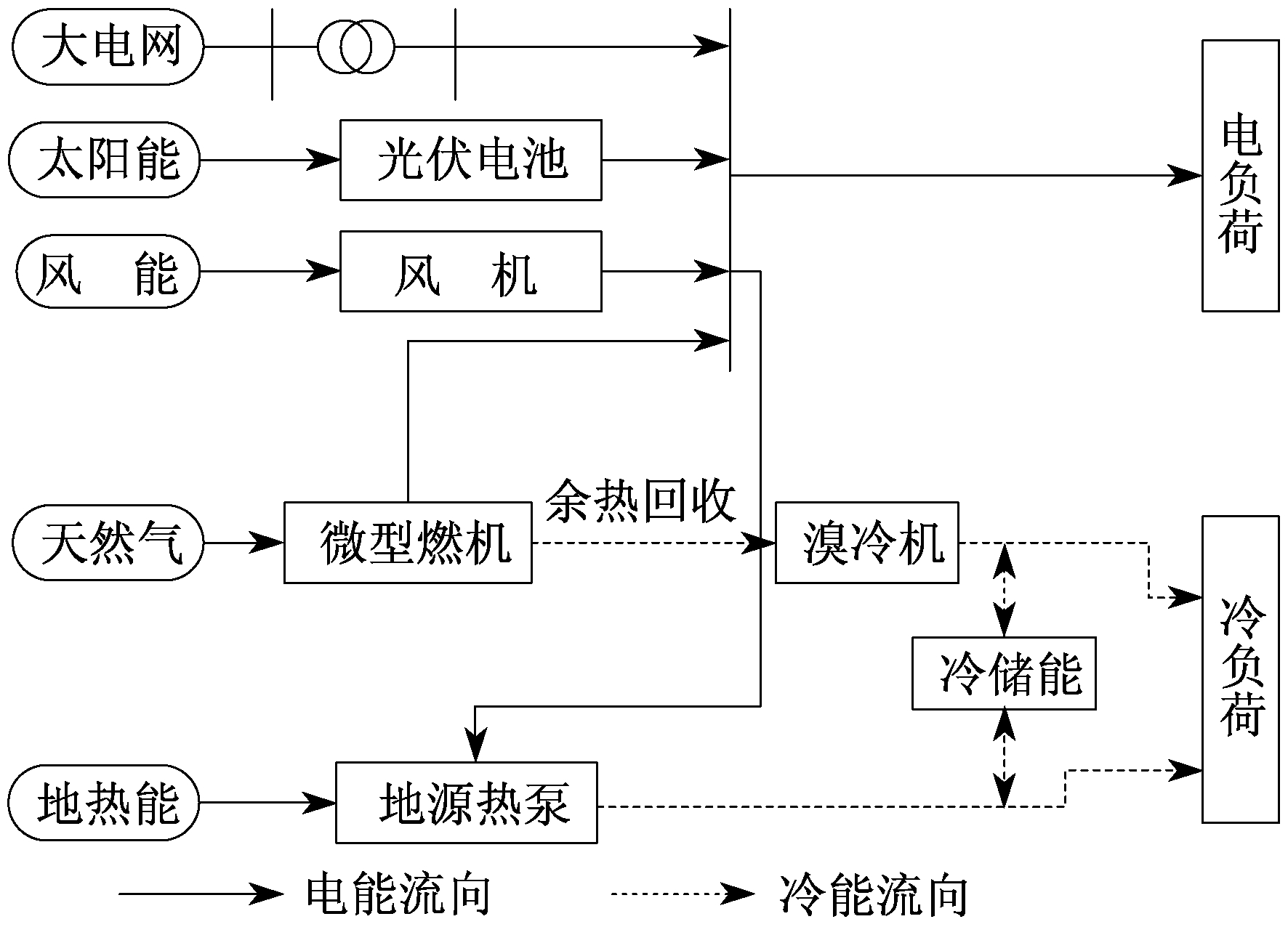
本文以夏季某城区建筑的CCP系统为研究对象。该系统包含WT、PV、微型燃机、溴冷机、HP以及CS等设备, 系统结构图如图 1所示。
CS的充放率为0.88, 自耗率为0.01, 储能荷电状态取值范围为[0, 0.9], 初始值为10 kWh, 容量为100 kWh; 溴冷机的制冷系数为1.36, 余热回收率为0.85; HP的制冷系数取4.5;供冷收益系数为Cco=0.1元/kWh。系统中各单元的机组维护费用系数及运行参数如表 1所示。
表 1
系统内各设备的运行参数
| 设备 类型 |
设备维护 费用/(元· kW-1) |
功率上限 | 功率下限 | 散热损失 系数 |
| kW | ||||
| PV | 0.025 | |||
| WT | 0.029 | |||
| MT | 0.025 | 60 | 15 | 0.15 |
| HP | 0.026 | 30 | 0 | |
| 大电网 | 60 | -60 | ||
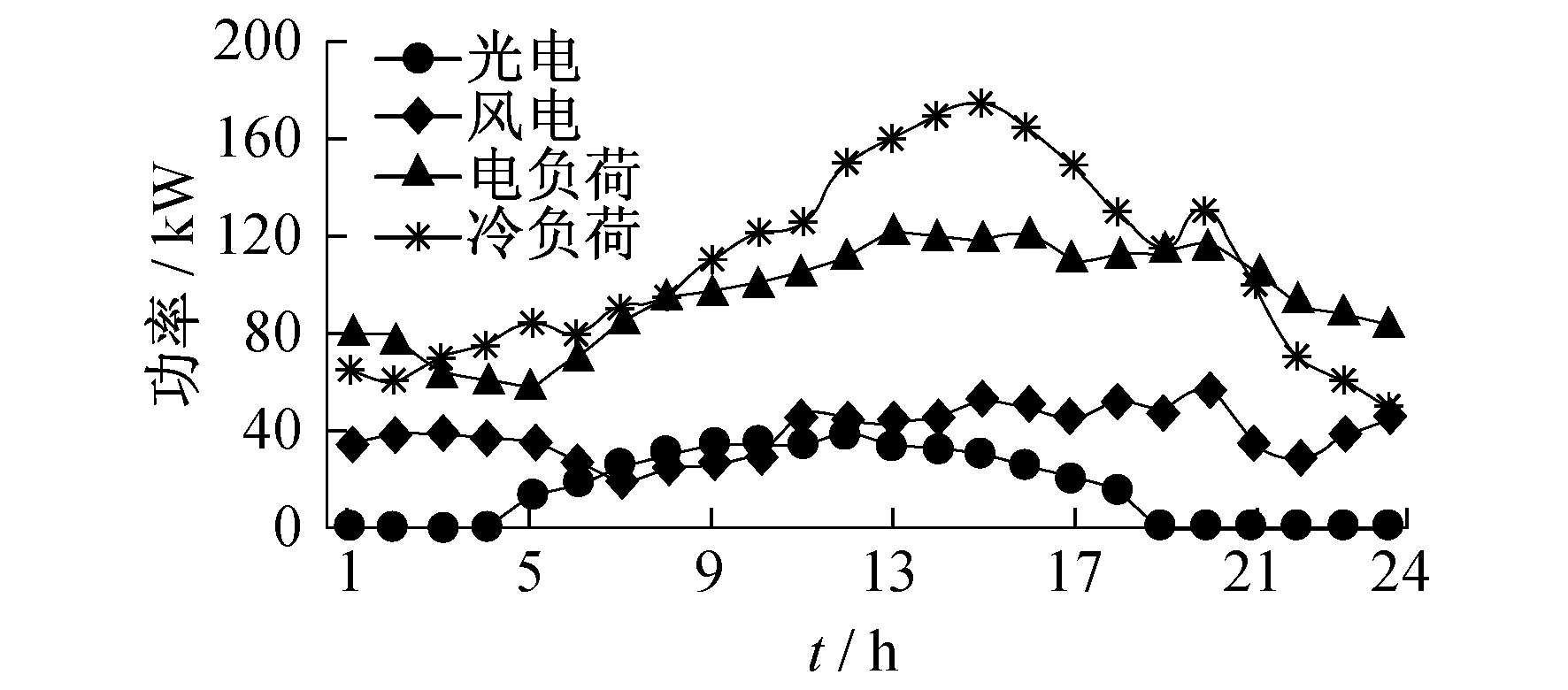
根据夏季用户的需求, 负荷需求可分为冷负荷和电负荷。夏季风电、光电、冷负荷及电负荷的日预测曲线如图 3所示, 优化调度周期为24 h, 单位时间段为1 h。采用自适应布谷鸟算法进行求解, 种群规模为200, 最大迭代次数为100次, 发现概率为0.25。
电价采用峰谷平电价政策, 具体价格如表 2所示。其中, 峰时段为10:00~13:00和19:00~22:00, 平时段为7:00~9:00和14:00~18:00, 谷时段为1:00~6:00和23:00~24:00。
表 2
电价表元·kWh-1
| 时段 | 购电价格 | 售电价格 |
| 峰时段 | 0.83 | 0.63 |
| 平时段 | 0.55 | 0.30 |
| 谷时段 | 0.17 | 0.13 |
3.2 优化结果分析
3.2.1 不含可再生能源和冷储能装置
为了研究本文模型的经济性, 利用不含风、光等可再生能源和冷储能装置的CCP系统优化调度模型进行对比。图 4为夏季供冷和供电优化调度结果。
不含可再生能源和冷储能装置的系统工作于“以冷定电”的运行模式, 系统的冷负荷优先使用溴冷机配合微型燃机产生的冷能, 缺额的部分由地源热泵消耗电能进行制冷补足。由图 4(a)可知:系统的冷负荷大部分由溴冷机承担, 由于微型燃机在工作过程中消耗燃料, 因此该调度模型的能源购买成本较高。图 4(b)可以看出, 系统的电负荷及HP消耗的电能由微型燃机和向大电网购买两部分组成。因微型燃机要跟随冷负荷的变化情况, 不能参与电能的调度, 因此余下的电能需要向大电网购买, 产生较高的购电费用, 导致该调度模型的综合运行成本较高。
3.2.2 含可再生能源和冷储能装置
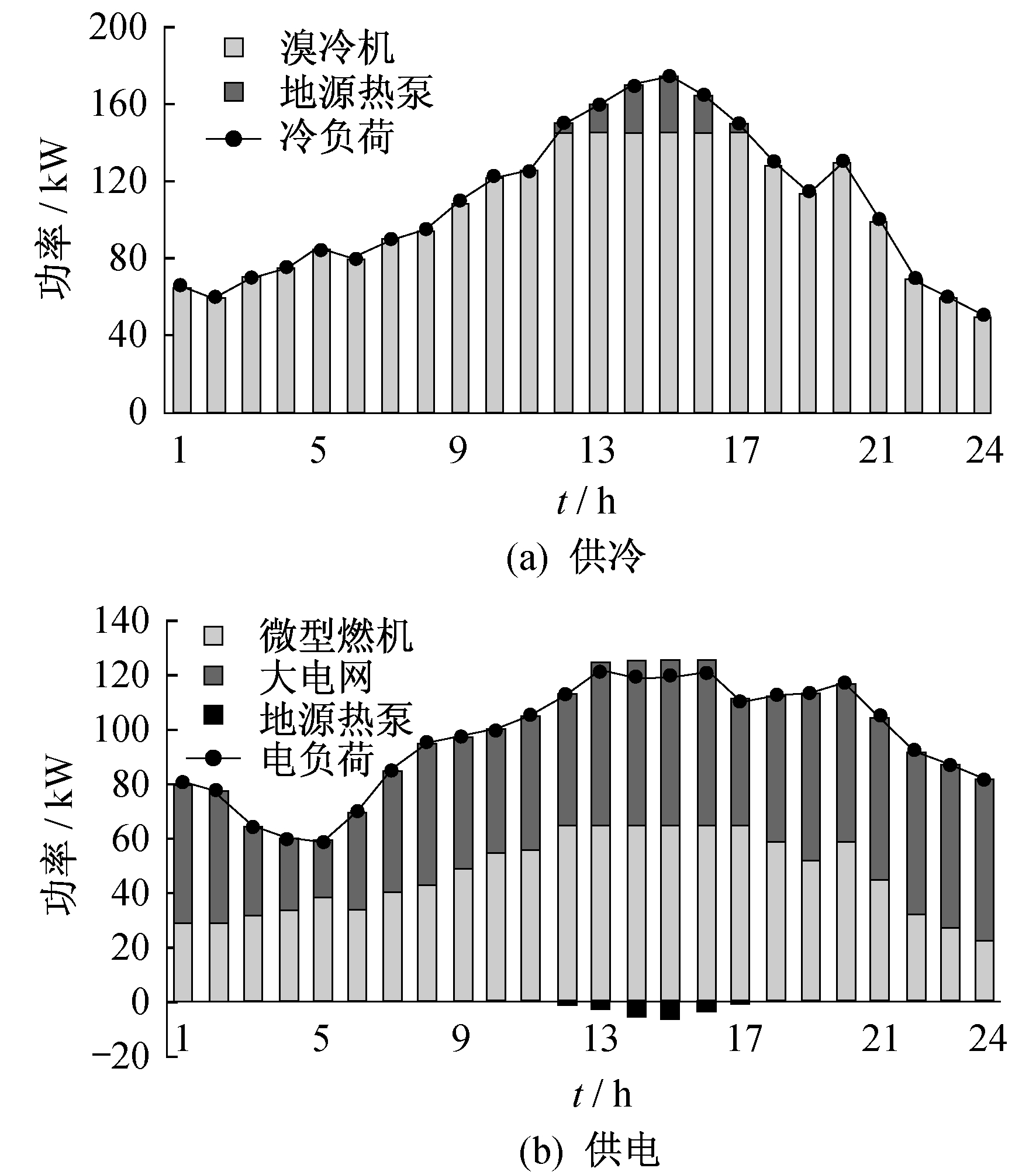
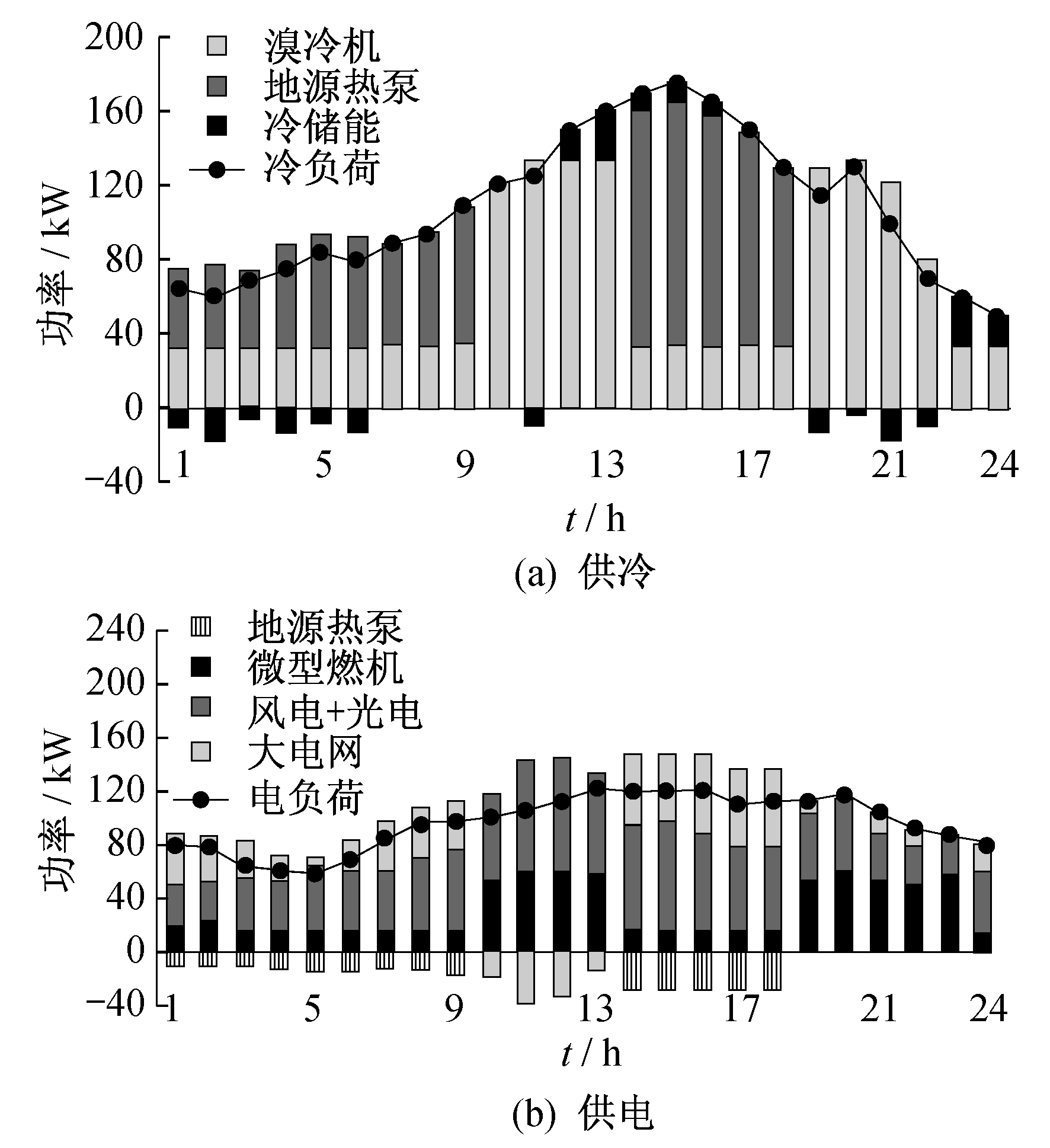
含风、光等可再生能源和冷储能装置的CCP系统的供冷、供电优化调度结果如图 5所示。
由图 5可看出:含有风、光等可再生能源和冷储能装置的系统内, 冷负荷需求由溴冷机配合微型燃机、地源热泵和冷储能装置共同满足, 而电负荷以及热泵制冷所需的电能由微型燃机、风电、光电以及与大电网交易共同承担。
在电价处于谷时段和平时段时, 微型燃机的发电成本高于购电价格, 由大电网供电比微型燃机发电更经济, 因此该时段微型燃机工作于最小功率输出工况下, 电负荷主要由风电、光电来满足, 缺额部分则向大电网购电进行补充。此时, 热泵的制冷成本低于溴冷机的供冷成本, 因此冷负荷主要由热泵消耗电能制冷供应, 少数冷负荷需求使用溴冷机配合微型燃机可提供的冷能, 多余的冷能由冷储能装置进行储存。
在电价处于峰时段时, 系统内的冷负荷和电负荷需求大幅增加, 由于购电价格高于微型燃机的发电成本, 因此电负荷优先消耗风电和光电, 剩余的部分由微型燃机来供应, 多余的电能售向大电网进行获益。此时的冷负荷主要由溴冷机配合微型燃机进行供应, 少数由冷储能装置释放冷能来满足。
由图 5(a)可以看出, 在整个调度过程中, 冷储能装置在冷负荷低谷时段进行蓄能, 在冷负荷需求高峰时段释放冷能, 充分发挥了其调峰调蓄的功能, 减少了系统运行的费用, 验证了本文模型的有效性和经济性。
3.2.3 获益-成本分析
上述两种调度模型的综合成本如表 3所示。其中, 环境成本仅计算CO2治理成本。
表 3
两种调度模型的综合成本对比
| 调度模型 | 综合成本 | 运行成本 | 环境成本 | |||
| 电网交互成本 | 维护成本 | 购买能源成本 | 供冷获益 | |||
| 不含可再生能源和冷储能 | 1 761.28 | 659.78 | 28.60 | 996.36 | 260.20 | 336.74 |
| 含可再生能源和冷储能 | 914.74 | 345.55 | 48.10 | 619.15 | 260.20 | 162.14 |
由表 3可知, 加入可再生能源和冷储能装置后, 电网交互成本减少了47.62%, 购买能源成本降低了37.86%, 排放CO2带来的环境成本减少了174.60元, 机组维护成本增加了19.50元, 究其原因在于增加了对光伏组件和风机的维护。因此, 冷电联供系统明显降低了综合成本, 达到了节能减排的目的, 具有良好的经济性和环保效益。
4 结语
为了提高系统的经济性、环保效益及可再生能源的利用率, 本文综合可再生能源及储能装置的运行特性, 建立了含多种可再生能源和储能的CCP优化调度模型, 并采用自适应布谷鸟算法进行求解, 提高了算法的收敛速度。算例仿真表明, 将可再生能源和冷储能装置引入CCP系统, 可有效降低系统的能源购买成本和环境成本, 减少机组的耗能量。模型兼顾了系统运行的环保性和节能性, 且冷储能装置可以调节系统内冷负荷的峰谷差, 具有一定的实际应用价值。
参考文献
-
[1]ROSTAMZADEH H, EBADOLLAHI M, GHAEBI H, et al. Comparative study of two novel micro-CCHP systems based on organic Rankine cycle and Kalina cycle[J]. Energy Conversion and Management, 2019(1): 210-229.
-
[2]多可再生能源冷热电联供微网系统环境经济优化调度[J]. 控制与决策, 2015, 31(5): 913-918.
-
[3]LI L X, YU S W, MU H L, et al. Optimization and evaluation of CCHP systems considering incentive policies under different operation strategies[J]. Energy, 2018, 162: 825-840. DOI:10.1016/j.energy.2018.08.083
-
[4]能源互联网规划研究综述及展望[J]. 中国电机工程学报, 2017, 37(22): 6445-6462.
-
[5]JIANG Z H, HAN J, LIU W Z, et al. Energy internet-a new driving force for sustainable urban development[J]. Energy Procedia, 2018(9): 1206-1211.
-
[6]考虑储热装置的风电-热电机组联合优化运行策略[J]. 电力自动化设备, 2017, 37(6): 139-145.
-
[7]含电转气和热电解耦热电联产机组的区域能源互联网联合经济调度[J]. 电网技术, 2018, 42(11): 3512-3520.
-
[8]计及燃料电池热-电综合利用的能源网日前调度优化策略[J]. 中国电机工程学报, 2019, 39(6): 1603-1613.
-
[9]考虑风电消纳的热电联供型微网日前鲁棒经济调度[J]. 电力系统自动化, 2019, 43(4): 40-51. DOI:10.7500/AEPS20180214007
-
[10]考虑电能交互的冷热电多微网系统日前优化经济调度[J]. 电力系统自动化, 2018, 42(21): 36-46. DOI:10.7500/AEPS20180417006
-
[11]含热泵和储能的冷热电联供型微网经济运行[J]. 电网技术, 2018, 42(6): 1735-1743.
-
[12]LU S L, LI Y W, XIA H W. Study on the configuration and operation optimization of CCHP coupling multiple energy system[J]. Energy Conversion and Management, 2018(10): 773-791.
-
[13]考虑热电和大规模风电的电网调度研究综述[J]. 电力系统保护与控制, 2018, 46(15): 162-170. DOI:10.7667/PSPC171173
-
[14]缓冲水蓄能冷热电联供系统运行策略及性能分析[J]. 建筑热能通风空调, 2018, 37(3): 16-21. DOI:10.3969/j.issn.1003-0344.2018.03.004
-
[15]一种自适应步长布谷鸟搜索算法[J]. 计算机工程与应用, 2013, 49(10): 68-71. DOI:10.3778/j.issn.1002-8331.1112-0292