发布时间: 2019-10-10
摘要点击次数:
全文下载次数:
DOI: 10.3969/j.issn.1006-4729.2019.05.015
2019 | Volume 35 | Number 5

经济性预测控制的切换控制策略优化算法设计

蔡鹏程, 郑鹏远

上海电力学院自动化工程学院, 上海 200090

收稿日期: 2019-04-02

基金项目: 国家自然科学基金(61573239);教育部重点实验室开放课题(Scip201509)

中图法分类号: TP273

文献标识码: A

文章编号: 1006-4729(2019)05-0493-05

摘要

针对经济性预测控制优化问题, 设计了切换控制策略的优化算法。首先, 离线计算具有耗散性的Hessian矩阵指标; 其次, 在线优化阶段, 根据系统状态所处的不同可行域, 分别在经济指标优化和Hessian矩阵对应的动态指标优化之间进行切换, 从而驱动系统状态收敛到稳态工作点, 取得了较优的经济性能; 最后, 仿真结果验证了方法的有效性。

关键词

经济性预测控制; Hessian矩阵; 耗散性; 可行域; 切换控制

Economic Model Predictive Control Optimization Algorithm Based on Switching Control Strategy

CAI Pengcheng, ZHENG Pengyuan

School of Automation Engineering, Shanghai University of Electric Power, Shanghai 200090, China

Abstract

For the economic model predictive control, an optimization algorithm is proposed based on the switching control strategy.Firstly, the proposed optimization algorithm offline computes the Hessian matrix index with dissipativity.Secondly, according to the different feasible domains of the system state, it switches between the economic performance optimization and the dynamic performance optimization by use of the Hessian matrix online respectively.This method can drive the system state to converge to the steady state and achieve better economic performance.Finally, the simulation results demonstrates the validity of the proposed method.

Key words

economic predictive control; Hessian matrix; dissipativity; feasibility region; switching control

多年来, 动态系统的最佳过程操作和控制策略一直是工业界和学术界积极研究的课题, 引起了广泛关注。目前, 复杂工业过程的优化控制普遍采用由计划调度层、经济优化层(Real-Time Optimization, RTO)、先进控制层、基础控制层等不同功能层组成的分层递阶控制结构^[1]。由于其RTO层经济指标的优化并不涉及下层模型预测控制(Model Predictive Control, MPC)的动态模型信息, RTO层的静态优化模型和MPC动态模型通常具有不匹配性^[2-3]。

受到优化和控制一体化设计思想的驱动, 研究者们提出了将经济指标优化和动态控制以扁平化结构实现为特征的经济性预测控制(Economic Model Predictive Control, EMPC)^[4-9]。为了架起稳定性分析的桥梁, 保证系统状态收敛到系统稳态工作点, 文献[10-13]以耗散性为工具, 对经济性预测控制问题进行了分析和设计。其中文献[10-11]指出, 如果一个系统相对于其经济目标函数是严格耗散的, 则通过优化目标函数得到的经济控制器可以使系统渐进稳定。在可控性假设下, 耗散性也是系统在稳态工作点(x_s, u_s)时最优运行的充要条件^[11-13]。文献[14]通过在经济目标中添加凸性质的指标, 使得系统对于新的目标函数具有耗散性。文献[15-16]采用参数优化的形式来构造新目标函数, 以保证系统满足耗散性。在稳态工作点附近, 将原系统近似转化为线性化系统, 将原经济指标近似转化为Hessian矩阵对应的二次指标, 从而将原经济性能优化问题转化为动态性能优化问题, 进一步以系统状态和稳态工作点之间偏差的二次指标函数作为惩罚函数来优选控制量, 在稳态工作点附近取得了较优的控制性能。但当系统初始状态远离稳态工作点时, 转化后的动态优化问题将难以适用, 因此该设计方法存在一定的局限性, 有待进一步开展相关研究以改善系统性能。

本文以逼近原经济优化问题的最优性为设计目标, 引入切换控制思想^[17], 设计切换控制策略的经济性预测控制优化算法。该算法首先离线设计具有耗散性的Hessian矩阵指标, 随后根据系统状态所处的不同可行域, 分别在经济指标优化和Hessian矩阵对应的动态性能指标优化之间进行切换, 从而驱动系统状态收敛到稳态工作点, 并取得较优的经济性能。

1 问题描述

考虑连续时间非线性系统

$\dot{x}=f(x, u)$

(1)

式中:x——状态变量, x∈X⊆R^n_x;

u——输入变量, u∈U⊂R^n_x。

式(1)中, (x, u)⊆X×U。系统的经济指标采用连续函数l_e(x, u)进行定义, l_e:X×U→R。

对于式(1)和给定经济指标l_e(x, u), 系统的稳态工作点(x_s, u_s)满足

$l_{\mathrm{e}}\left(x_{\mathrm{s}}, u_{\mathrm{s}}\right)=\min\limits_{x, u}\left\{l_{\mathrm{e}}(x, u) \mid f(x, u)=0\right. , \\ x \in X, u \in U\}$

式(1)的经济性优化问题, 可描述为经济性预测控制优化问题, 其公式为

$ \min\limits_{u} J(x, u)=\int_{0}^{T} l_{\mathrm{e}}(x(t), u(t)) \mathrm{d} t $

(3)

$\begin{aligned} \text { s.t. } \quad \dot{x}(t) &=f(x(t), u(t)), \forall t \in[0, T] \\ & x(t) \in X, u(t) \in U, \forall t \in[0, T] \\ & x(0)=x_{0}, x(T)=x_{\mathrm{s}} \end{aligned}$

式中:x₀——系统初始状态。

求解上述经济性预测控制优化问题即是对式(3)进行滚动优化。在当前时刻将控制输入序列的第一个控制量u(0)施加到系统上, 驱动系统状态在下一时刻到达新的状态值, 再以新的系统状态值作为初始状态进行重复优化。

定义1 如果存在一个可微的储存函数V(x)满足

$\frac{\mathrm{d} V(x)}{\mathrm{d} t} \leqslant l_{\mathrm{e}}(x, u)-l_{\mathrm{e}}\left(x_{\mathrm{s}}, u_{\mathrm{s}}\right)$

(4)

则称式(1)在稳态工作点附近关于目标函数l_e(x, u)是耗散的, 如果式(4)不等条件严格成立, 则称式(1)在稳态工作点附近关于目标函数l_e(x, u)严格耗散。

2 性能指标转化

针对经济性预测控制优化问题(3), 将其转化为参考跟踪MPC问题^[16]。首先对原优化问题的经济指标进行转化, 即通过增加拉格朗日松弛项, 构建新性能指标为

$L(x, u, \lambda)=l_{\mathrm{e}}(x, u)+\lambda f(x, u)$

(5)

式中:λ——拉格朗日因子。

基于上述拉格朗日松弛后的新性能指标, 求解式(2)可等价转化为

$\min\limits_{x, u}\{L(x, u, \lambda) \mid f(x, u)=0 \\ x \in X, u \in U\}$

(6)

因此, 可以采用拉格朗日函数L(x, u, λ)代替经济目标函数l_e(x, u), 进行性能优化。

考虑等式约束优化问题:

$\quad \min\limits_{z} l(z) \\ \mathrm{s.t.} \quad h(z)=0$

(7)

假设函数l(z)二次可微, 并且函数h(z)可微, 给定一个点z^*和z^*附近的扰动量Δz=z-z^*, 则函数l(z)可以在点z^*泰勒级数展开为

$ \begin{aligned} l\left(z^{*}+\Delta z\right) \approx & l\left(z^{*}\right)+\nabla l\left(z^{*}\right) \Delta z+\\ & \frac{1}{2} \Delta z^{\mathrm{T}} \nabla^{2} l\left(z^{*}\right) \Delta z \end{aligned} $

(8)

式中: l(z^*)——l(z)在点z^*的梯度;

²l(z^*)——l(z)在点z^*的Hessian矩阵。

同理, 约束函数h(z)可以展开为

$h\left(z^{*}+\Delta z\right) \approx h\left(z^{*}\right)+\nabla h\left(z^{*}\right) \Delta z$

(9)

假设z^*是式(7)的解, 则其满足式(7)最优解的必要条件为

$\nabla l\left(z^{*}\right)+\lambda^{\mathrm{T}} \nabla h\left(z^{*}\right)=0$

(10)

$h\left(z^{*}\right)=0$

(11)

进一步得出, 等式(10)可以表示为L(z^*, λ)=0, 其中L(z^*, λ)是与式(7)相关的拉格朗日函数。式(7)的经济目标函数l(z)能够替换成L(z, λ), 并且在z^*处泰勒级数展开为

$ \begin{array}{c} L(z, \lambda) \approx L\left(z^{*}, \lambda\right)+\frac{1}{2}\left(z-z^{*}\right)^{\mathrm{T}} \cdot \\ \nabla^{2} L\left(z^{*}, \lambda\right)\left(z-z^{*}\right) \end{array} $

(12)

式中: ²L(z^*, λ)——L(z, λ)在z^*处的Hessian矩阵。

在z^*点附近, 该优化目标函数可转化成Hessian矩阵指标。

3 优化问题转化

针对式(1), 经济目标函数为l_e(x, u), 稳态工作点为(x_s, u_s), 在稳态工作点(x_s, u_s)处对f(x, u)进行线性化, 并对L(x, u, λ)进行泰勒级数展开^[16]

f(x, u)≈f(x_s, u_s)+

$f(x, u) \approx f\left(x_{\mathrm{s}}, u_{\mathrm{s}}\right)+ \\ \underbrace{\left.\frac{\partial f(x, u)}{\partial x}\right|_{x_{\mathrm{s}}} \partial x}_{\boldsymbol{A}_{\mathrm{c}}}+\underbrace{\left.\frac{\partial f(x, u)}{\partial u}\right|_{u_{\mathrm{s}}} \partial u}_{\boldsymbol{B}_{\mathrm{c}}}$

(13)

$L(x, u, \lambda) \approx L\left(x_{\mathrm{s}}, u_{\mathrm{s}}, \lambda\right)+ \\ \underbrace{\nabla^{\mathrm{T}} L\left(x_{\mathrm{s}}, u_{\mathrm{s}}, \lambda\right)}_{\boldsymbol{G}}\left[\begin{array}{c}x-x_{\mathrm{s}} \\ u-u_{\mathrm{s}}\end{array}\right]+ \\ \frac{1}{2}\left[\begin{array}{l}x-x_{\mathrm{s}} \\ u-u_{\mathrm{s}}\end{array}\right]^{\mathrm{T}} \underbrace{\nabla^{2} L\left(x_{\mathrm{s}}, u_{\mathrm{s}}, \lambda\right)}_{\boldsymbol{H}}\left[\begin{array}{l}x-x_{\mathrm{s}} \\ u-u_{\mathrm{s}}\end{array}\right]$

(14)

$\boldsymbol{H}=\nabla^{2} L\left(x_{\mathrm{s}}, u_{\mathrm{s}}, \lambda\right)$

(15)

式(14)中, G=0, f(x_s, u_s)=0, L(x_s, u_s, λ)在稳态工作点(x_s, u_s)处为常值。

式(1)在稳态工作点处相对于其目标函数不一定具有耗散性。为保证系统的耗散性, 基于式(15)中得到的Hessian矩阵H, 以对称矩阵P_c和H_c为变量, 以线性矩阵不等式为约束条件^[15-16], 即

$ \left[\begin{array}{cc} \boldsymbol{A}_{\mathrm{c}}^{\mathrm{T}} \boldsymbol{P}_{\mathrm{c}}+\boldsymbol{P}_{\mathrm{c}} \boldsymbol{A}_{\mathrm{c}} & \boldsymbol{P}_{\mathrm{c}} \boldsymbol{B}_{\mathrm{c}} \\ \boldsymbol{B}_{\mathrm{c}}^{\mathrm{T}} \boldsymbol{P}_{\mathrm{c}} & 0 \end{array}\right]+\boldsymbol{H}+\boldsymbol{H}_{\mathrm{c}} \leqslant 0 $

(16)

通过最小化对称矩阵H_c的某一合适矩阵范数, 从而计算得到对称矩阵H_c。

利用式(15)和式(16)计算所得的矩阵H和H_c, 令

$ \hat{\boldsymbol{H}}=\boldsymbol{H}+\boldsymbol{H}_{\mathrm{c}} $

(17)

将式(3)转化为如下优化问题

$ \min\limits_{u-u_{\mathrm{s}}} \frac{1}{2} \int_{0}^{T}\left[\begin{array}{c} x(t)-x_{\mathrm{s}} \\ u(t)-u_{\mathrm{s}} \end{array}\right]^{\mathrm{T}} \hat{\boldsymbol{H}}\left[\begin{array}{c} x(t)-x_{\mathrm{s}} \\ u(t)-u_{\mathrm{s}} \end{array}\right] \mathrm{d} t $

(18)

$\begin{array}{ll}\text { s. t. } & \dot{x}=\boldsymbol{A}_{\mathrm{c}}\left(x(t)-x_{\mathrm{s}}\right)+\boldsymbol{B}_{\mathrm{c}}\left(u(t)-u_{\mathrm{s}}\right)\end{array} \\ x(t) \in X, u(t) \in U, \forall t \in[0, T] \\ x(0)=x_{0}, x(T)=x_{\mathrm{s}}$

通过式(17)计算所得的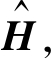一定满足耗散性。特别当H_c=0时, 说明H自身已满足耗散性条件, 则有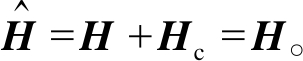在式(18)中, 已将原经济指标转化为矩阵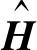所对应的二次指标函数, 进而将式(3)转化为参考跟踪MPC(t-MPC)控制问题, 即采用t-MPC控制设计方法优化系统的经济性。

4 经济性预测控制的切换控制优化算法

在上述分析过程中, 原经济性优化问题被转化成具有Hessian矩阵二次目标函数的动态性能优化问题。需要指出的是, 这种近似等价关系仅在稳态点附近成立。当系统状态远离稳态工作点时, 这种近似等价关系就难以成立, 导致该优化难以获得较优的经济性能。为了弥补上述缺陷, 本文以初始点和稳态工作点间的欧氏距离为切换条件, 设计基于切换控制策略的优化算法。

4.1 离线计算

步骤1 分别采用式(15)计算H, 式(13)计算A_c和B_c, 式(16)计算H_c, 式(17)计算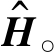

步骤2 设定稳态工作点附近小邻域的半径值ρ=c₁和Ω_ρ={x∈Rⁿ|(x-x_s)²≤ρ²}, 切换时间t_switch=c₂。

4.2 在线优化

步骤1 对式(3)进行求解, 并将优化计算所得的控制量施加到受控系统上。

步骤2 判断系统状态是否位于Ω_ρ, 优化时间是否到达切换时间t_switch。若x∈Ω_ρ或t≥t_switch, 则执行步骤3, 否则返回步骤1。

步骤3 对转化后的式(18)进行求解, 将控制量u施加到受控系统上, 并重复进行滚动优化, 直至系统状态驱动到稳态工作点时, 优化结束。

在上述经济性预测控制的切换控制优化算法中, 当系统状态在Ω_ρ领域以外时, 求解原经济性能优化问题, 从而追求系统的经济性能最优; 当系统位于稳态工作点的设定邻域或到达设定时间时, 则切换为t-MPC动态性能优化问题进行求解, 所得到的控制输入量可以驱动系统状态收敛至稳态工作点。

5 仿真验证

考虑非线性连续流式搅拌罐反应器, 系统模型如下

$ \left\{\begin{array}{l} \dot{x}_{1}=1-10^{4} x_{1}^{2} \mathrm{e}^{-\frac{1}{x_{3}}}-400 x_{1} \mathrm{e}^{-\frac{0.55}{x_{3}}}-x_{1} \\ \dot{x_{2}}=10^{4} x_{1}^{2} \mathrm{e}^{-\frac{1}{x_{3}}}-x_{2} \\ \dot{x_{3}}=u-x_{3} \end{array}\right. $

(19)

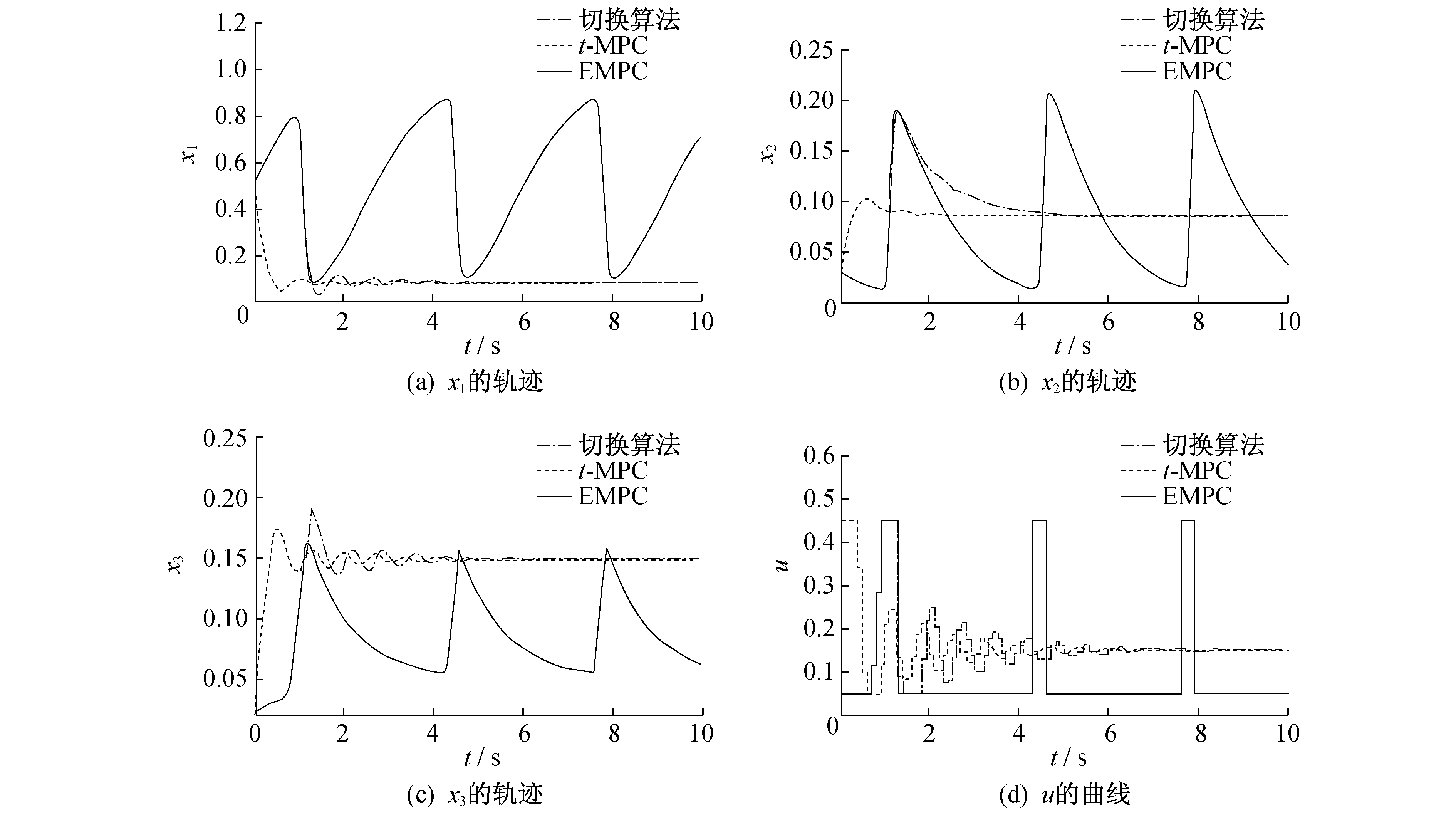
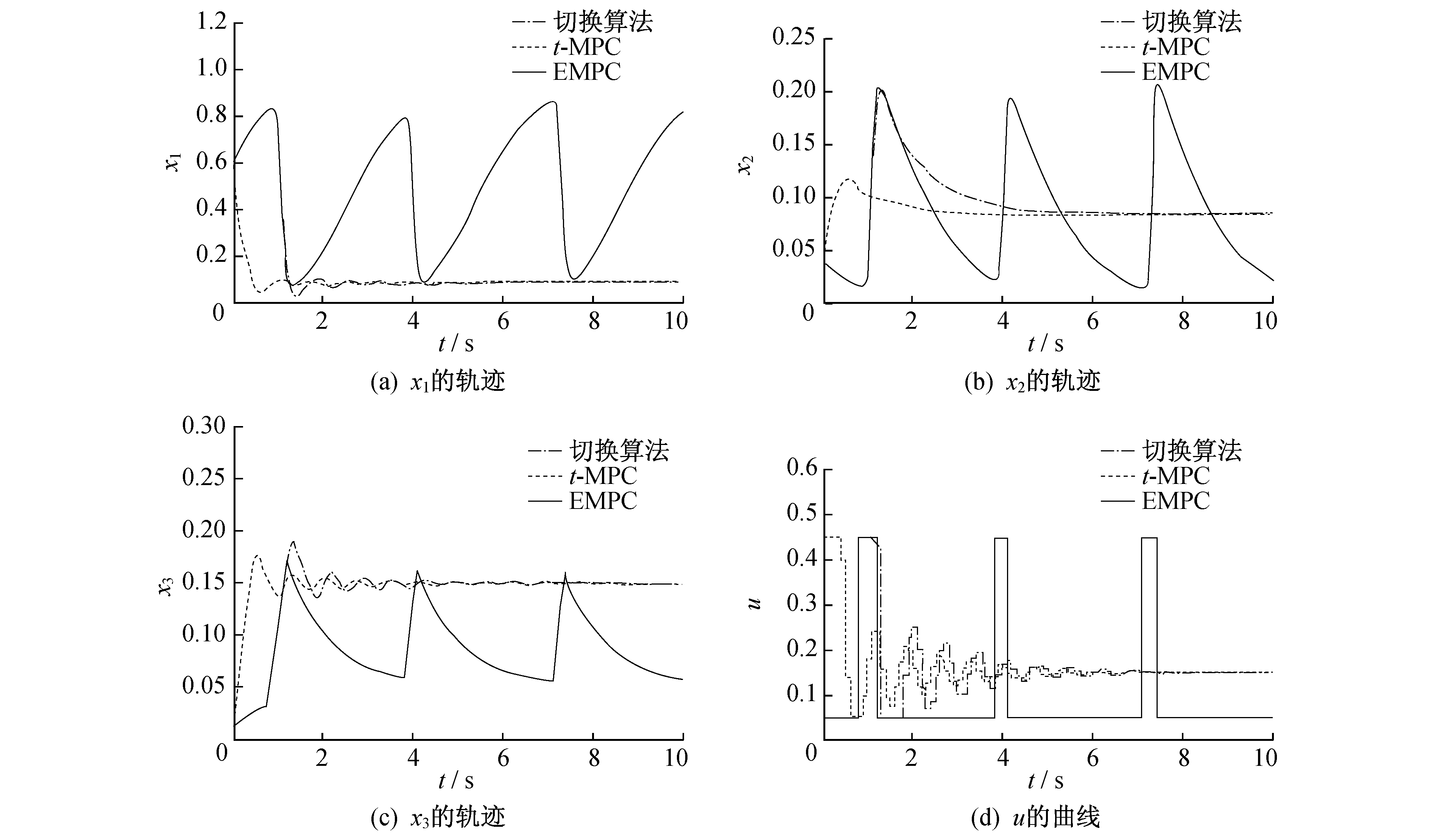
该生产过程的经济优化目标是使x₂最大化, 经济优化目标为l_e(x, u)=-1.0×10⁴x₂, 系统的稳态工作点为x_s=[0.083 2, 0.084 6, 0.149 1], u_s=0.149 1。选取输入约束0.049≤u≤0.449, 拉格朗日乘子λ=[-0.156 1, -1, 0], 优化时域T=10 s, 采样时间t_c=0.1 s。将原经济性预测控制算法标记为“EMPC”, 将式(18)记为“t-MPC”, 将本文设计的经济性预测控制切换控制优化算法标记为“切换算法”。选取系统初始状态x(0)=[0.5, 0.03, 0.02]和x(0)=[0.6, 0.04, 0.01], 分别记为“状态1”和“状态2”, 对上述3种算法的控制效果进行仿真验证, 由离线计算得到稳态工作点所对应的A_c, B_c, H, H_c分别为

$\boldsymbol{H}=\left[\begin{array}{cccc}-20.632\;3 & 0 & -38.594\;6 & 0 \\ 0 & 0 & 0 & 0 \\ -38.594\;6 & 0 & -65.004 & 0 \\ 0 & 0 & 0 & 0\end{array}\right], \\ \boldsymbol{H}_{\mathrm{c}}=\left[\begin{array}{cccc}-0.1276 & -0.0188 & -0.0776 & 0.0056 \\ -0.0188 & 0.0035 & 0.0153 & -0.0005 \\ -0.0776 & 0.0153 & 0.0817 & 0.0076 \\ 0.0056 & -0.0005 & 0.0076 & 0.1882\end{array}\right] , \\ \boldsymbol{A}_{\mathrm{c}}=\left[\begin{array}{ccc}-13.0349 & 0 & -24.3921 \\ 2.0341 & -1 & 3.8064 \\ 0 & 0 & -1\end{array}\right], \boldsymbol{B}_{\mathrm{c}}=\left[\begin{array}{l}0 \\ 0 \\ 1\end{array}\right] 。$

采用ICLOCS优化软件, 利用内点优化算法IPOPT^[18]来求解此优化问题, 得到闭环系统的仿真结果分别如图 1和图 2所示。平均经济性能和动态性能统计如表 1所示。

图 1 状态1下的闭环系统轨迹

图 2 状态2下的闭环系统轨迹

表 1 两种状态下的性能统计结果

下载CSV

算法	平均经济性能		动态性能
算法	状态1	状态2	状态1	状态2
EMPC	-805	-827	995	976
t-MPC	-855	-884	0.002 8	0.004 2
切换算法	-1 206	-1 303	172	201

由图 1和图 2可以看出, 在原经济性预测控制算法控制下, 被控系统处于震荡状态, 没有收敛到稳态工作点; t-MPC算法和本文设计的切换控制优化算法均可以驱动系统状态收敛到稳态工作点。由表 1可以看出, 与t-MPC算法相比, 切换算法虽然在收敛速度上慢一些(动态性能上有一定的差距), 但在3种方法中可以取得最优的经济性能。

6 结语

本文针对经济性预测控制优化问题, 离线计算了Hessian矩阵, 并通过求解线性矩阵不等式优化问题, 构造了满足耗散性条件的二次指标函数, 将经济性预测控制优化问题转化为跟踪MPC问题。本文设计的切换控制策略的优化算法, 驱动系统状态收敛到稳态工作点, 有效地改善了系统的经济性能。

参考文献

[1]

QIN S J, BADGWELL T A. A survey of industrial model predictive control technology[J]. Control Engineering Practice, 2003, 11(7): 733-764. DOI:10.1016/S0967-0661(02)00186-7

[2]

ENGELL S. Feedback control for optimal process operation[J]. Journal of Process Control, 2007, 17(3): 203-219. DOI:10.1016/j.jprocont.2006.10.011

[3]

SEQUEIRA E, GRAELLS M, PUIGJANER L. Real-time evolution of online optimization of continuous process[J]. Industrial Engineering Chemical Research, 2002, 41(7): 1815-1825. DOI:10.1021/ie010464l

[4]

HOVGAARD T G, LARSEN L F, JORGENSEN J B. Flexible and cost efficient power consumption using economic MPC: a supermarket refrigeration benchmark[C]//The 50th IEEE Conference on Decision and Control and European Control Conference. Orlando, FL, USA, 2011: 848-854.

[5]

HOVGAARD T G, IDLUND K, JORGENSEN J B. The potential of economic MPC for power management[C]//The 49th IEEE Conference on Decision and Control, CDC 2010. Atlanta, Georgia, USA, 2010: 7533-7538.

[6]

HOVGAARD T G, LARSEN L F, JORGENSEN J B. Robust economic MPC for a power management scenario with uncertainties[C]//The 50th IEEE Conference on Decision and Control and European Control Conference. Orlando, FL, USA, 2011: 1515-1520.

[7]

RAWLINGS J B, AMRIT R. Optimizing process economic performance using model predictive control, in nonlinear model predictive control[M]//MAGNI L, RAIMONDO D M, ALLGOWER F. Lecture Notes in Control and Information Sciences. Berlin, Germany: Springer, 2009: 119-138.

[8]

ASKE E, STRAND S, SKOGESTAD S. Coordinator mpc for maximizing plant throughput[J]. Computers & Chemical Engineering, 2008, 32(1/2): 195-204.

[9]

ZAVALA V, BIEGLER L. The advanced step nmpc controller: Optimality, stability and robustness[J]. Automatica, 2009, 45(1): 86-93. DOI:10.1016/j.automatica.2008.06.011

[10]

AMRIT R, RAWLINGS J B, ANGELI D. Economic optimization using model predictive control with a terminal cost[J]. Annual Reviews in Control, 2011, 35: 178-186. DOI:10.1016/j.arcontrol.2011.10.011

[11]

ANGELI D, AMRIT R, RAWLINGS J. On average performance and stability of economic model predictive control[J]. IEEE Trans Autom Control, 2012, 57: 1615-1626. DOI:10.1109/TAC.2011.2179349

[12]

MULLER M A, ANGELI D, ALLGOWER F. On convergence of averagely constrained economic MPC and necessity of dissipativity for optimal steady-state operation[C]//Proceeding of the American Control Conference. Washington, DC, USA, 2013: 3141-3146.

[13]

FAULWASSER T, KORDA M, JONES C, et al. Turnpike and dissipativity properties in dynamic real-time optimization and economic MPC[C]//Proceedings of the 53rd IEEE Conference on Decision and Control. Los Angeles, CA, USA, 2014: 2734-2739.

[14]

ANGELI D, AMRIT R, RAWLINGS J. Enforcing convergence in nonlinear economic MPC[C]//The 50th IEEE Conference on Decision and Control and European Control Conference. Orlando, FL, USA, 2011: 3387-3391.

[15]

MAREE J P, IMSLAND L. Performance and stability for combined economic and regulatory control in MPC[C]//Proceedings of the 19th IFAC World Congress. Cape Town, South Africa, 2014: 639-645.

[16]

OLANREWAJU O I, MACIEJOWSKI J M. Economic equivalence of economic model predictive control and hierarchical control schemes[J]. Industrial & Engineering Chemistry Research, 2016, 55(41): 10978-10989.

[17]

基于控制器状态跟随的微电网平滑切换控制方法[J]. 上海电力学院学报, 2014, 30(6): 495-499.

[18]

WACHTER A, BIEGLER L T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming[J]. Math Program, 2006, 106(1): 25-57. DOI:10.1007/s10107-004-0559-y