|
|
|
发布时间: 2019-12-10 |
|
|
|
|
收稿日期: 2019-09-17
中图法分类号: TM621
文献标识码: A
文章编号: 1006-4729(2019)06-0535-04
|
摘要
随着1 000 MW超超临界燃煤发电机组的扩建应用, 对锅炉的风烟系统提出了更高的要求。以某电厂的HU27046-221型引风机为例进行分析研究, 提出了一种基于改进自回归滑动平均(ARMA)预测模型的电厂风机状态预测方法。首先, 采用数据挖掘理论对引风机原始数据进行相关性分析; 其次, 采用改进ARMA方法对引风机相关状态参数进行预测; 最后, 与传统的ARMA预测方法进行对比分析, 结果表明所提出的方法预测精度较高。
关键词
自回归滑动平均; 数据挖掘; 相关性分析; 电厂风机; 状态预测
Abstract
With the expansion and application of the 1 000 MW ultra-supercritical coal-fired generating unit, higher requirements are imposed on the boiler's flue gas and air system.This paper takes the HU27046-221 induced draft fan of a power plant in Huadian Jiangsu as an example for analysis and research, and proposes a state prediction method based on improved ARMA for power plant fans.Firstly, the data mining theory is used to analyze the correlation data of the induced draft fan.Secondly, the improved ARMA method is used to predict the relevant state parameters of the induced draft fan.Finally, compared with the traditional ARMA prediction method, the prediction accuracy of the method is high.
Key words
autoregressive moving average; data mining; correlation analysis; autoregressive moving average; power plant fans state prediction
目前, 电力企业一般采用定期巡检的方式对电厂设备进行计划性检修, 在此过程中不仅造成了电厂设备的利用率较低, 也产生了较高的维修费用和较长的维修周期。同时, 随着自动化水平的提高, 电厂设备每时每刻都在产生海量的历史数据, 这些数据中隐藏着有关设备运行状态的关键信息, 如何从这些高维度的海量数据中挖掘出有价值的信息显得尤为重要。
文献[1]通过对电力设备的状态检修进行分析, 提出了一种应用于电力设备时变停运的模型, 结合计划检修对设备可用度的影响, 可为后续状态检修中的检修决策和风险评估提供一定的借鉴。文献[2]采用改进的灰色模型对某电厂给水泵冷油器出口油温进行了状态参数的预测, 预测精度较高, 可应用于电厂点检数据的处理。文献[3]采用L-M优化算法对设备的运行状态进行了预测, 结果表明该算法误差精度高, 收敛速度快, 可满足设备运行状态预测的要求。文献[4]通过对海量的工业运行数据进行挖掘分析, 提出了一种工业设备状态预警算法, 对提高设备可靠性和优化维修策略等具有重要的实用意义。
1 数据挖掘相关理论
数据挖掘是知识发现中的一个核心步骤, 是从海量、随机、模糊的数据中挖掘出有实用价值的知识和信息的过程[5-7]。常见的分析方法包括回归分析、相关性分析、聚类分析、主成分分析和因子分析等。
相关性分析法用来描述两个变量之间的密切程度, 通过对两个变量进行相关性分析, 保留相关性小的变量, 剔除相关性大的变量, 以达到对数据进行降维的目的。假设两个变量U和V, 则两者之间的皮尔逊相关系数为
| $ \begin{aligned} \rho_{U, V}=& \frac{\operatorname{cov}(U, V)}{\sigma_{U} \sigma_{V}}=\\ & \frac{E(U V)-E(U) E(V)}{\sqrt{E\left(U^{2}\right)-E^{2}(U)} \sqrt{E\left(V^{2}\right)-E^{2}(V)}} \end{aligned} $ | (1) |
式中:cov——协方差;
E——数学期望;
σ——均方差。
一般规定如下:ρ=0~0.2为不相关或极弱相关; ρ=0.2~0.4为弱相关; ρ=0.4~0.6为中等强度相关; ρ=0.6~0.85为强相关; ρ=0.85~1为极强相关。
2 改进ARMA预测模型
自回归滑动平均(Auto-regressive Moving Average, ARMA)模型由美国统计学家JENKINS和BOX提出, 是一种时间序列分析的方法, 被广泛应用于时间序列数据的建模分析中[8-10]。
ARMA预测模型包含q个移动平均项和p个自回归项, 已知一个时间序列{xt}, (t=1, 2, 3…), ARMA预测模型公式为
| $ X_{t}=c+\varepsilon_{t}+\sum\limits_{i=1}^{p} \varphi_{i} X_{t-i}+\sum\limits_{j=1}^{q} \theta_{j} \varepsilon_{t-j} $ | (2) |
式中:Xt——待估参数;
c——序列均值;
εt, εt-j——白噪声序列;
φi——自回归系数;
θj——滑动平均系数。
记Mh为h步滞后算子, 则有
| $M^{h} x_{t}=x_{t-k}$ | (3) |
若忽略常数项, 自回归模型AR(p)和移动平均模型MA(q)可分别表示为
| $ \varepsilon_{t}=\varphi(M) X_{t}=\left(1-\sum\limits_{i=1}^{p} \varphi_{i} M^{i}\right) X_{t} $ | (4) |
| $ X_{t}=\theta(M) \varepsilon_{t}=\left(1+\sum\limits_{i=1}^{q} \theta_{i} M^{i}\right) \varepsilon_{t} $ | (5) |
综上, ARMA预测模型可表示为
| $ \left(1+\sum\limits_{i=1}^{q} \theta_{i} M^{i}\right) \varepsilon_{t}=\left(1-\sum\limits_{i=1}^{p} \varphi_{i} M^{i}\right) X_{t} $ | (6) |
ARMA预测模型针对的是平稳时间序列, 但在实际应用中, 所采集的时间序列一般都是非平稳随机序列, 且受季节等因素的影响, 预测精度较低。因此, 本文在ARMA预测模型基础上融合了差分操作和季节性差分环节, 不仅将非平稳时间序列转化为平稳时间序列, 更考虑了季节性因素的影响, 使得预测结果更加准确。
改进后的ARMA预测模型为
| $\varphi_{f}(B) \phi_{F}\left(B^{s}\right)(1-B)^{d}\left(1-B^{s}\right)^{D} y_{t}= \\ \theta_{g}(B) \Psi_{G}\left(B^{s}\right) u_{t}$ | (7) |
式中:φf(B)——非季节自回归多项式;
f——非季节AR项阶数;
B——滞后算子;
φF(Bs)——季节自回归多项式;
F——季节AR项阶数;
s——季节周期长度;
d——非季节差分的次数;
D——季节差分的次数;
yt——非平稳序列;
θg(B)——非季节滑动平均多项式;
g——非季节MA项阶数;
ΨG(Bs)——季节移动平均特征多项式;
G——季节MA项阶数;
ut——高斯噪声。
3 应用实例
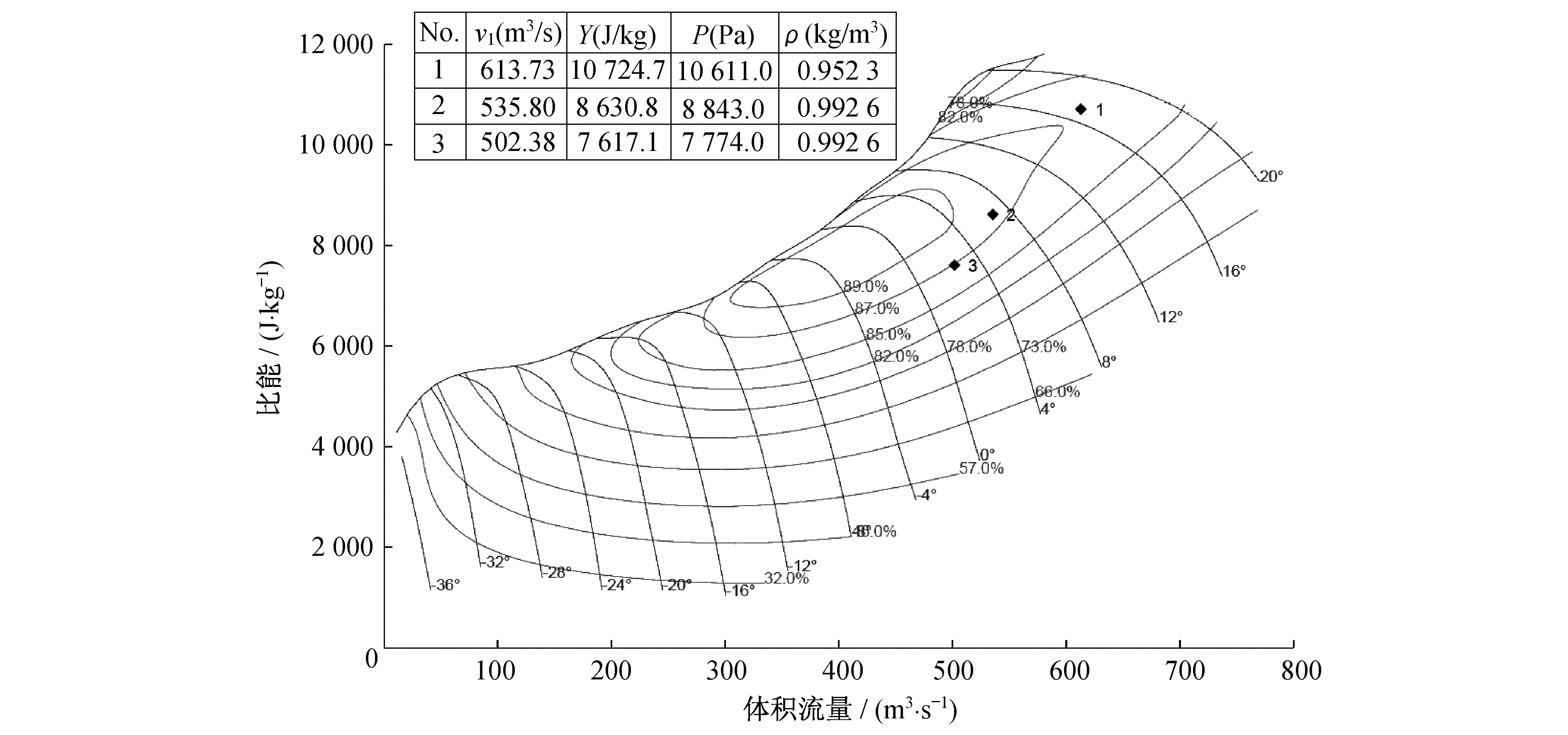
本文以某电厂二期2×1 000 MW超超临界燃煤发电机组配套锅炉的节能型轴流式引风机为例进行分析, 引风机型号为HU27046-221。在转速为745 r/min下, 引风机的性能曲线如图 1所示。表 1为引风机的相关参数表。
表 1
引风机的相关参数
| 参数名称 | TB工况 | BMCR工况 | ECR工况 |
| 风机转速/(r·min-1) | 745 | 745 | 745 |
| 风机入口静压/Pa | -6 493 | -5 411 | -4 757 |
| 风机出口静压/Pa | 4 118 | 3 432 | 3 017 |
| 风机全压效率/% | 86.4 | 87.6 | 87.0 |
| 入口粉尘含量/(mg·m-3) | < 50 | < 50 | |
| 入口烟气密度/(kg·m-3) | 0.952 3 | 0.992 6 | 0.992 6 |
| 风机入口流量/(m3·s-1) | 613.73 | 535.8 | 502.38 |
| 酸露点温度/℃ | 103.2 | 103.2 | 103.2 |
| 烟气含湿量/(g·kg-1) | 58.5 | 58.5 | 58.5 |
| 入口烟气温度/℃ | 105 | 90 | 90 |
现从该厂厂级监控系统(Safety Instrumented System, SIS)中选取与HU27046-221引风机相关的测点共20个, 采集2019年7月15日09:00至2019年7月23日09:00期间共20×2 593个状态的正常历史数据, 采样间隔为5 min。其中, 2019年7月15日09:00至2019年7月21日09:00的数据用于状态预测模型的建立, 2019年7月21日09:00至2019年7月23日09:00的数据用于状态预测模型的验证, 采样间隔为5 min。
通过数据挖掘理论中的相关分析法对上述正常历史数据进行相关性分析。对于与引风机运行状态相关的20个测点, 按相关性大小进行排序, 选取6个与引风机运行状态相关的主要状态参数, 包括引风机X向轴振、引风机Y向轴振、引风机前轴承温度(3个)、电机前轴承温度(2个)、电机润滑油压力和电机电流等, 共计9个测点的历史数据。从最初的20个测点压缩至9个测点, 达到了对原始正常的历史数据降维的目的, 减少了数据的冗余问题。
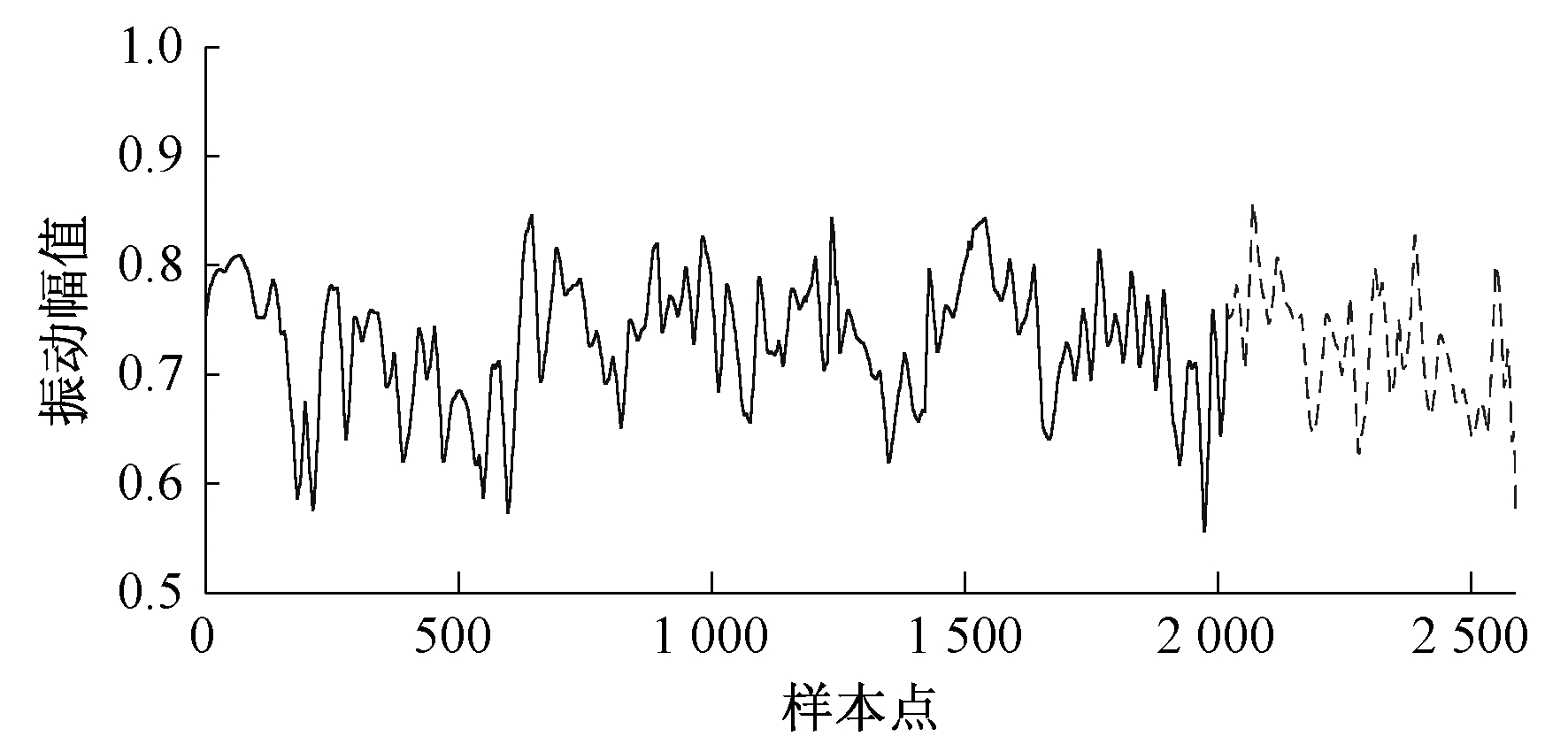
现对2019年7月15日09:00至2019年7月21日09:00期间共9×2017个正常的历史数据采用改进ARMA预测模型进行建模, 将2019年7月21日09:00至2019年7月23日09:00期间共9×577个正常的历史数据用于预测模型的验证。以HU27046-221引风机X轴向振动为例, 振动原始信号和预测信号趋势如图 2所示。图 2中, 实线为2019年7月15日09:00至2019年7月21日09:00(前2 017个样本点)期间正常的历史数据, 虚线(后577个样本点)为采用改进ARMA预测模型预测的趋势。
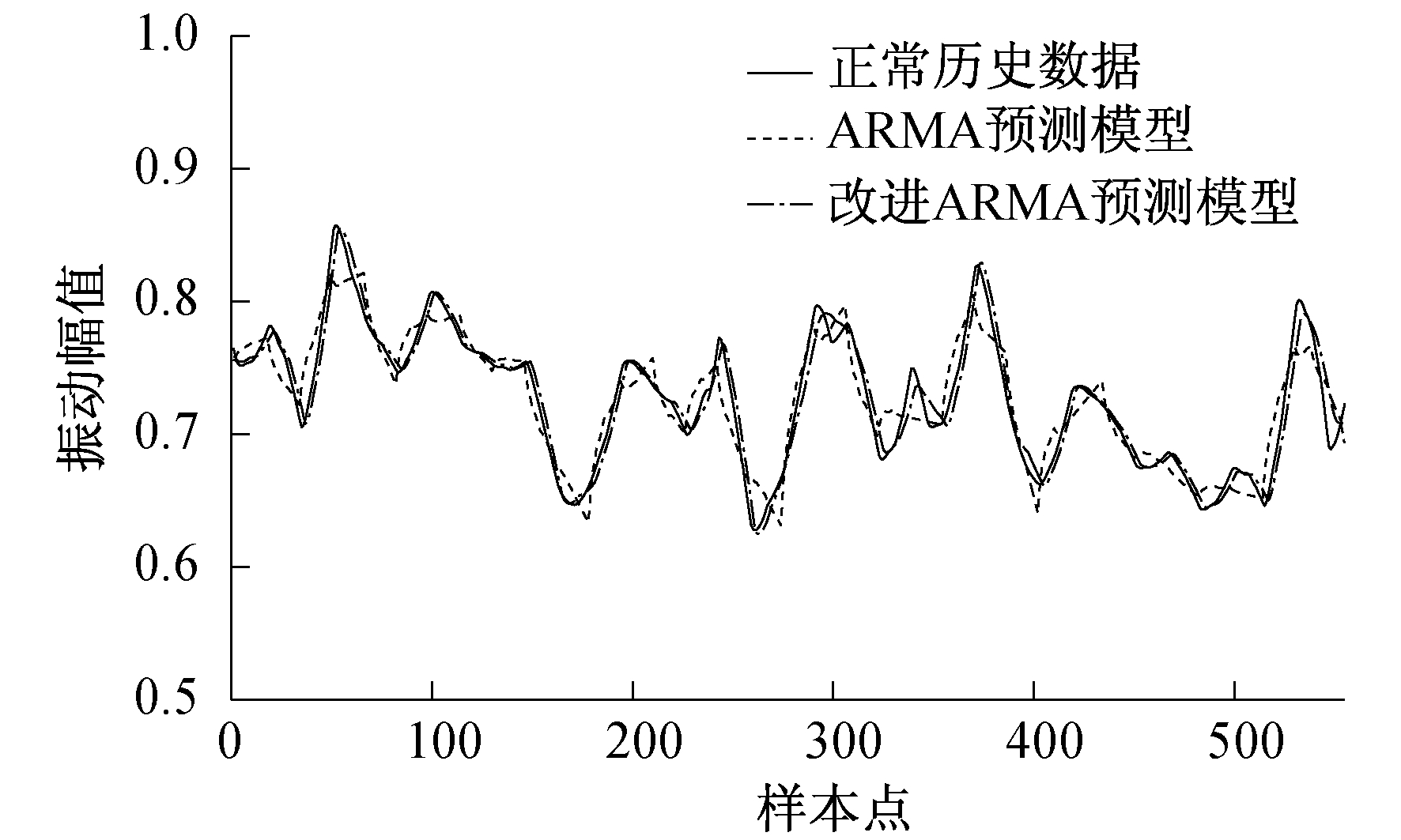
图 3为采用改进ARMA预测模型对2019年7月21日09:00至2019年7月23日09:00(共577个样本点)进行引风机X轴向振动参数状态预测的曲线图。由图 3可知, 采用改进ARMA预测模型较ARMA预测模型的误差更小。经计算, 采用改进ARMA预测模型的均方根误差为0.025 5, ARMA预测模型的均方根误差为0.040 3。因此, 采用改进ARMA预测模型的预测精度较高, 可满足引风机状态预测工程实践的要求。
4 结语
针对电厂引风机运行条件复杂多变、极易发生故障的问题, 本文从高维度、海量的原始历史数据出发, 提出了一种基于改进ARMA的电厂风机状态预测方法。与传统的ARMA预测方法进行对比分析发现, 改进ARMA预测模型的预测精度较高, 可满足引风机状态预测工程实践的要求。
参考文献
-
[1]一种适用于状态检修的电力设备时变停运模型[J]. 中国电机工程学报, 2013, 33(25): 139-146.
-
[2]某电厂发电设备可靠性建模及状态预测[J]. 华电技术, 2019, 41(6): 27-32. DOI:10.3969/j.issn.1674-1951.2019.06.006
-
[3]采用L-M优化算法的设备状态预测[J]. 现代制造工程, 2012(3): 114-118. DOI:10.3969/j.issn.1671-3133.2012.03.029
-
[4]一种基于海量数据挖掘的设备状态预测算法[J]. 计算机科学, 2012, 39(增刊1): 318-321.
-
[5]王文东.模糊文本聚类算法的研究与应用[D].西安: 西安电子科技大学, 2012.
-
[6]王文娟.基于数据挖掘的电厂设备检修决策支持系统的研究[D].北京: 华北电力大学, 2011.
-
[7]马博洋.火电厂一次风机故障预警系统的应用研究[D].北京: 华北电力大学, 2016.
-
[8]电厂热工过程ARMA多参数辨识模型及应用[J]. 热力发电, 2000(2): 37-39. DOI:10.3969/j.issn.1002-3364.2000.02.011
-
[9]风力发电机状态预测与故障诊断的研究[J]. 华东电力, 2013, 41(12): 2561-2566.
-
[10]高洪福.优化组合模型在电厂设备状态预测中的研究与应用[D].北京: 中国石油大学, 2016.