发布时间: 2019-12-10
摘要点击次数:
全文下载次数:
DOI: 10.3969/j.issn.1006-4729.2019.06.004
2019 | Volume 35 | Number 6

碳纤维与玻璃钢风力机叶片动力特性的对比分析

张建平¹, 张智伟², 纪海鹏¹, 韩熠¹

1. 上海电力学院, 上海 200090;

2. 上海绿色环保能源有限公司, 上海 200433

收稿日期: 2018-12-19

基金项目: 上海市科学技术委员会项目(18DZ1202105, 18DZ1202302)

中图法分类号: TK83

文献标识码: A

文章编号: 1006-4729(2019)06-0531-04

摘要

以NREL 5 MW风力机叶片为研究对象, 分析了碳纤维与玻璃钢(GRP)材料的叶片和风轮在静止工况下的模态频率与振型, 对比了两种叶片在额定工况下的应力与位移。研究结果表明:两种材料的叶片均表现出较高的抗扭能力, 碳纤维风轮的抗摆振能力更强; 碳纤维与GRP叶片位移及应力分布相似, 刚度较低的GRP叶片使得其位移响应值很大、应力响应值相对较小。

关键词

碳纤维; 玻璃钢; 风力机叶片; 位移; 应力

Comparative Analysis of Dynamic Characteristics Between Carbon Fiber and GRP Wind Turbine Blades

ZHANG Jianping¹, ZHANG Zhiwei², JI Haipeng¹, HAN Yi¹

1. Shanghai University of Electric Power, Shanghai 200090, China;

2. Shanghai Green Environmental Protection Energy Co., Ltd., Shanghai 200433, China

Abstract

Taking NREL 5 MW wind turbine blades as the research object, the modal frequencies and shapes of carbon fiber and glass reinforced plastic (GRP) blades and wind turbines under static conditions are analyzed, and the stresses and the displacements of the two blades under rated conditions are compared.The results show that the blades of both materials exhibit high torsion resistance, and the carbon fiber wind wheel has stronger anti-shimmy ability.The displacement and stress distributions of carbon fiber and GRP blades are similar, and the lower stiffness of GRP blades makes the displacement response value larger and the stress response value smaller.

Key words

carbon fiber; glass reinforced plastic; wind turbine blades; displacement; stress

我国风力机叶片的主要原材料是树脂和增强体材料, 树脂有不饱和聚酯树脂、环氧树脂、乙烯基树脂, 增强体材料有玻璃纤维、碳纤维, 以及碳纤维和玻璃纤维混杂材料^[1]。碳纤维的性能一般优于玻璃钢(Glass Reinforced Plastic, GRP), 具有轻质坚固、抗腐蚀性强、易加工等特点^[2], 同时碳纤维材料的密度与GRP非常接近, 属于轻质材料^[3]。基于上述优点, 碳纤维材料在风力机以及军事装备制造^[4]、飞行器制造^[5]等领域都受到了青睐。

国内外学者在碳纤维与GRP材料叶片方面开展了一系列研究。在叶片应力分布的研究上, 王昊等人^[6]对GRP风力机叶片的多种应力进行了分析, 发现应力集中于叶片中部; QIN Z W等人^[7]对叶片根部在极限襟翼情况下的复合板结构强度进行了研究, 发现主梁内截面和根部过渡区纤维破坏指数较大, 纤维破坏分布与应力分布相反。在叶片模态的研究上, DE T等人^[8]采用玻璃纤维和碳纤维的混合材料铺层, 分析了各截面的应力分布和叶片的模态特性, 为碳纤维在5 MW级风力机叶片上的应用提供了理论参考; 杨海如等人^[9]设计了碳纤维复合材料风力机叶片, 并与树脂叶片进行了对比, 发现碳纤维叶片的固有频率高于树脂叶片。在两种材料的对比研究上, MELTEM A K等人^[10]综述了碳纤维复合材料和玻璃纤维复合材料的切削性能; ZHAO Z K等人^[11]制备了短碳纤维和短玻璃纤维复合材料, 并对其力学性能和摩擦学性能进行了比较; BALOKAS G等人^[12]比较了碳纤维与玻璃纤维复合材料叶片的应力分布和位移。目前, 国外知名叶片厂商已将碳纤维材料应用到新设计的叶片上, 例如丹麦LM Glassfiber“未来”叶片家族中61.5 m长、5 MW风机叶片在梁和根部都选用了碳纤维材料; 德国叶片制造商Nordex Rotor新制造的56 m长、5 MW风机叶片与Vestas Wind System制造的44 m长、3 MW风力机叶片的梁结构均采用了碳纤维材料; 其他厂商如Gamesa、NEG Micon、Enercon GmbH等也在新型大型叶片中使用了碳纤维^[13]。

随着各大制造商逐步将碳纤维应用于风力机叶片, 探究碳纤维与传统GRP叶片动力特性的差异就变得十分迫切。因此, 本文对NREL 5 MW碳纤维与GRP风力机叶片的模态、位移和应力进行了对比分析。

1 特征值方程

旋转状态下, 风力机叶片或风轮的结构域控制方程所对应于某一时刻t+Δt的有限元离散运动微分方程为

$\boldsymbol{M} \ddot{\delta}+\boldsymbol{C} \dot{\delta}+\boldsymbol{K} \delta=\boldsymbol{F}$

(1)

式中:M, C, K——叶片的质量矩阵、阻尼矩阵和刚度矩阵;

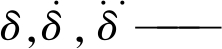有限元节点的位移、速度和加速度;

F——叶片载荷向量。

式(1)中, 令F为零向量, 则叶片处于自由振动状态, 这里K=K₀+K_a, K₀和K_a分别为小变形结构刚度矩阵与动刚度矩阵。在求解结构的模态频率时, 不考虑阻尼作用, 式(1)可转化为以下特征值方程

$ \boldsymbol{K} \boldsymbol{\phi}_{i}=\omega_{i}^{2} \boldsymbol{M} \boldsymbol{\phi}_{i} $

(2)

式中:ω_i, φ_i——第i(i=1, 2, 3, …)阶模态的模态频率、特征向量。

2 两种材料的动力特性

利用UG软件建立NREL 5 MW的碳纤维和GRP材料叶片和风轮的模型, 通过ANSYS软件计算得到静止工况下两种材料叶片和风轮的模态频率与振型, 并对比静止工况下NREL 5 MW的碳纤维和GRP材料叶片、风轮的前十阶振动模态。为了对比两种材料叶片的动力特性, 计算额定工况下两种材料叶片的位移与应力, 比较额定转速与来流风速下NREL 5 MW碳纤维和GRP叶片的位移分布与最大位移响应, 并分析两种材料的应力分布与最大Mises应力响应。

碳纤维和GRP两种材料简化为各向同性材料, 其等效性能参数^[14-15]如表 1所示。

表 1 材料性能参数

下载CSV

材料	弹性模量/GPa	泊松比	密度/ $\left(\mathrm{g} \cdot \mathrm{cm}^{-3}\right)$
碳纤维	228.00	0.25	1.78
GRP	17.60	0.17	1.70

2.1 静止工况下叶片和风轮模态

对轴杆进行固支约束, 其余部分自由振动, 通过数值模拟可得到两种叶片和风轮的前十阶模态。通过观察两种材料叶片振型图可以得到两种叶片的振型。由于振型图篇幅过长, 这里不予给出。叶片各阶频率与振型如表 2所示。为了观察两种材料构建的三叶片风轮模态, 这里也给出了碳纤维和GRP风轮的各阶频率与振型, 分别如表 3和表 4所示。由于风轮振型图所占篇幅过长, 因此在此也不给出。

表 2 两种材料叶片的前十阶固有频率与振型

下载CSV

阶次	频率/Hz		振型
阶次	碳纤维	GRP	振型
一阶	1.3219	0.3757	挥舞振动
二阶	3.5728	1.0158	挥舞与摆振混合振动
三阶	4.1952	1.1921	挥舞与摆振混合振动
四阶	8.4561	2.4023	挥舞振动
五阶	11.7290	3.3372	摆振振动占主导, 挥舞较不明显
六阶	15.1100	4.2921	挥舞振动
七阶	23.3170	6.6243	挥舞振动占主导, 摆振较不明显
八阶	25.7920	7.3412	摆振振动占主导, 挥舞较不明显
九阶	33.2420	9.4387	挥舞振动
十阶	35.8310	10.5270	扭转振动

表 3 碳纤维风轮前十阶模态频率与振型

下载CSV

阶次	频率/Hz	对称性	振型
一阶	1.321 3	单一阶不对称	挥舞振动
二阶	1.321 3	单一阶不对称	挥舞振动
三阶	1.323 2	单一阶对称	挥舞振动
四阶	3.523 2	单二阶对称	挥舞振动占主导, 摆振较不明显
五阶	3.597 1	单二阶不对称	挥舞振动占主导, 摆振较不明显
六阶	3.597 1	单二阶不对称	挥舞振动占主导, 摆振较不明显
七阶	4.179 6	单三阶对称	挥舞振动占主导, 摆振较不明显
八阶	4.207 0	单三阶不对称	挥舞振动占主导, 摆振较不明显
九阶	4.207 0	单三阶不对称	挥舞振动占主导, 摆振较不明显
十阶	8.440 0	单四阶不对称	挥舞振动占主导, 摆振较不明显

表 4 GRP风轮前十阶模态频率与振型

下载CSV

阶次	频率/Hz	对称性	振型
一阶	0.375 5	单一阶不对称	挥舞振动
二阶	0.375 5	单一阶不对称	挥舞振动
三阶	0.376 1	单一阶对称	挥舞振动
四阶	1.002 9	单二阶对称	挥舞与摆振混合振动
五阶	1.022 2	单二阶不对称	挥舞与摆振混合振动
六阶	1.022 2	单二阶不对称	挥舞与摆振混合振动
七阶	1.188 3	单三阶对称	挥舞振动占主导, 摆振较不明显
八阶	1.195 0	单三阶不对称	挥舞振动占主导, 摆振较不明显
九阶	1.195 0	单三阶不对称	挥舞振动占主导, 摆振较不明显
十阶	2.397 4	单四阶不对称	挥舞振动占主导, 摆振较不明显

从表 2可以看出:碳纤维叶片同一阶次的模态频率明显高于GRP, 而且其差值随着阶次的升高不断增大; 两种材料叶片的振型相同, 且均仅在第十阶出现扭转振动, 说明两种材料叶片的抗扭能力较强, 文献[16]-[17]佐证了这一结论。

对比表 2、表 3和表 4中模态频率, 可以发现:两种材料的风轮每三阶模态频率基本相当; GRP材料风轮频率较低, 是由于碳纤维的弹性模量和刚度远大于GRP的缘故; 每一种材料风轮的每三阶模态频率对应于单叶片某一阶模态频率, 譬如, 风轮的一至三阶频率对应于叶片的第一阶, 风轮的四至六阶频率对应于叶片的第二阶, 以此类推。当激励频率与结构固有频率接近时, 会导致结构因共振发生破坏, 因此在使用碳纤维和GRP作为风力机叶片材料时, 应尽量避免载荷和运行相关频率接近表 3和表 4中的模态频率。

由表 3和表 4中的模态振型可知:两种材料风轮振型主要以挥舞为主, 摆振的影响较低, 且两种材料风轮的对称振型都出现在第三、四、七阶; 碳纤维风轮部分阶次的摆振相比于GRP材料更不明显, 说明GRP风轮抗摆振能力更弱。

2.2 额定工况下叶片位移和应力

本文计算了NREL 5 MW碳纤维与GRP叶片在额定来流风速和额定转速工况下的位移分布、最大位移响应。

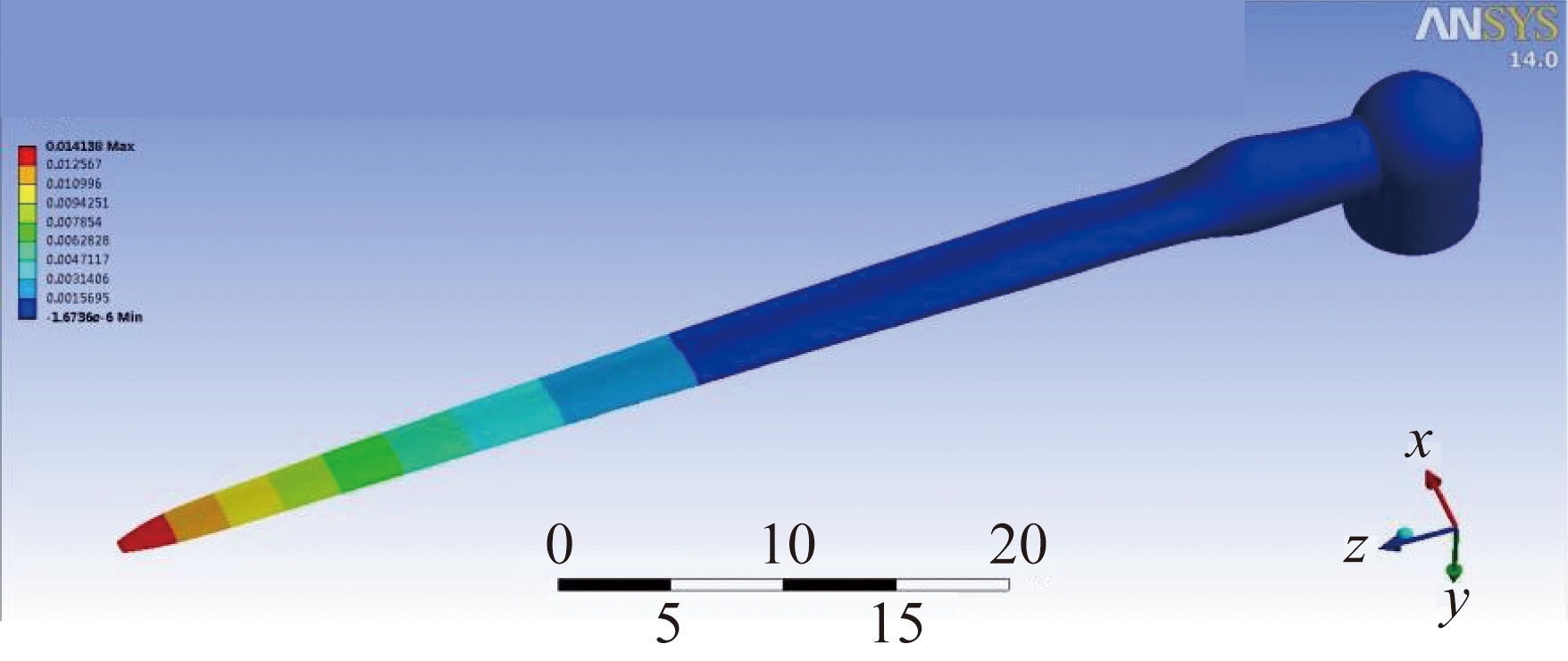
经过对比发现, 两种材料叶片的位移分布相差不大。这里仅给出了碳纤维叶片的位移分布, 如图 1所示。由图 1可以看出, 从叶根至叶尖位移逐步增大, 最大位移均出现在叶尖区域。

图 1 碳纤维叶片位移分布

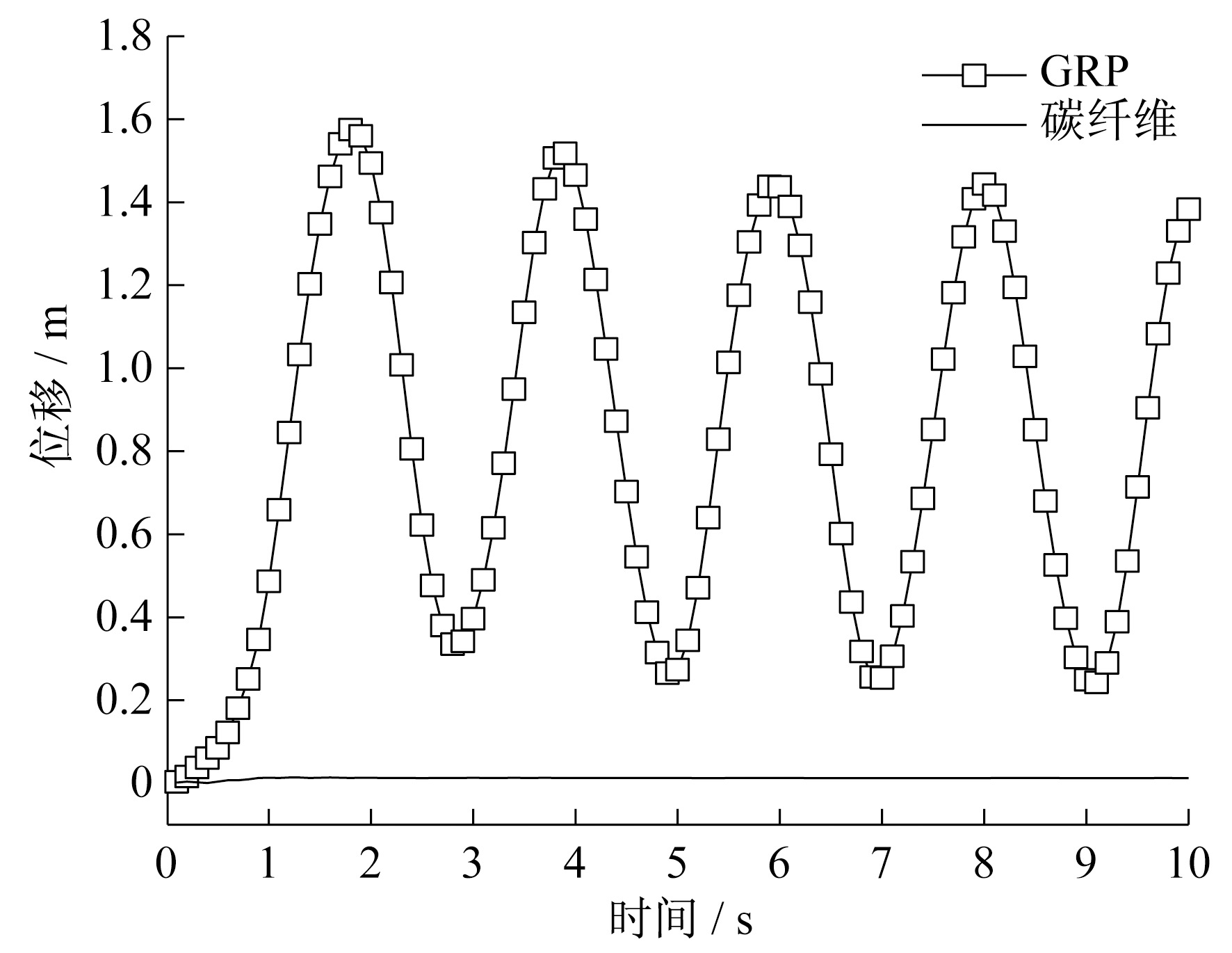
图 2给出了碳纤维和GRP叶片挥舞方向的最大位移响应。由图 2可知:1 s之后同一时刻的GRP叶片位移远远高于碳纤维, 因此碳纤维叶片位移响应曲线看似一条直线; GRP叶片位移最大峰值为1.57 m, 碳纤维叶片位移峰值仅为0.014 m, 这是由于碳纤维的刚度远高于GRP所致。

图 2 叶片最大位移响应

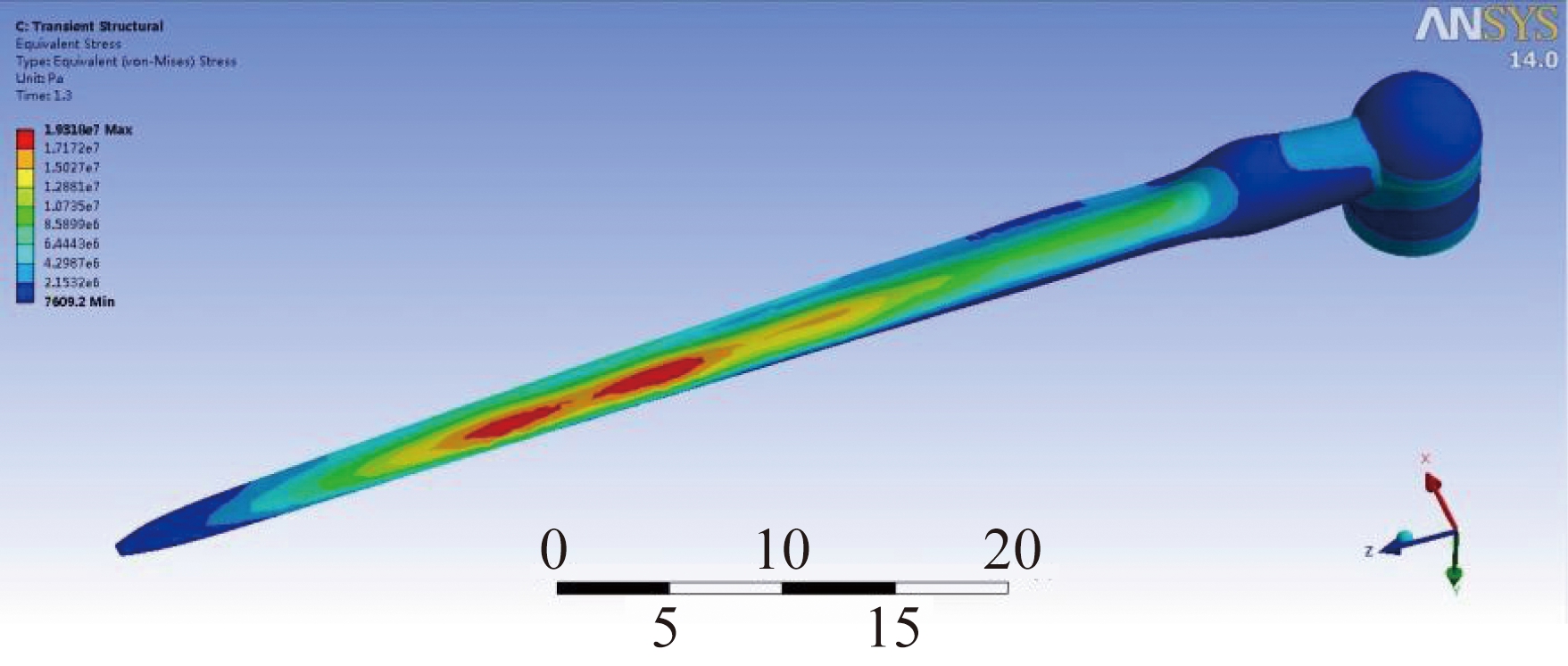
同样, 碳纤维与GRP叶片应力分布较为相似。图 3给出了碳纤维叶片Mises应力分布。由图 3可以看出, 叶片中部位置出现应力峰值, 长期运行时可能导致叶片在该处产生裂纹甚至断裂, 因此在设计制造后应对两种材料叶片中部进行强度校核, 以确保风力机在运行中的安全。

图 3 碳纤维叶片Mises应力分布

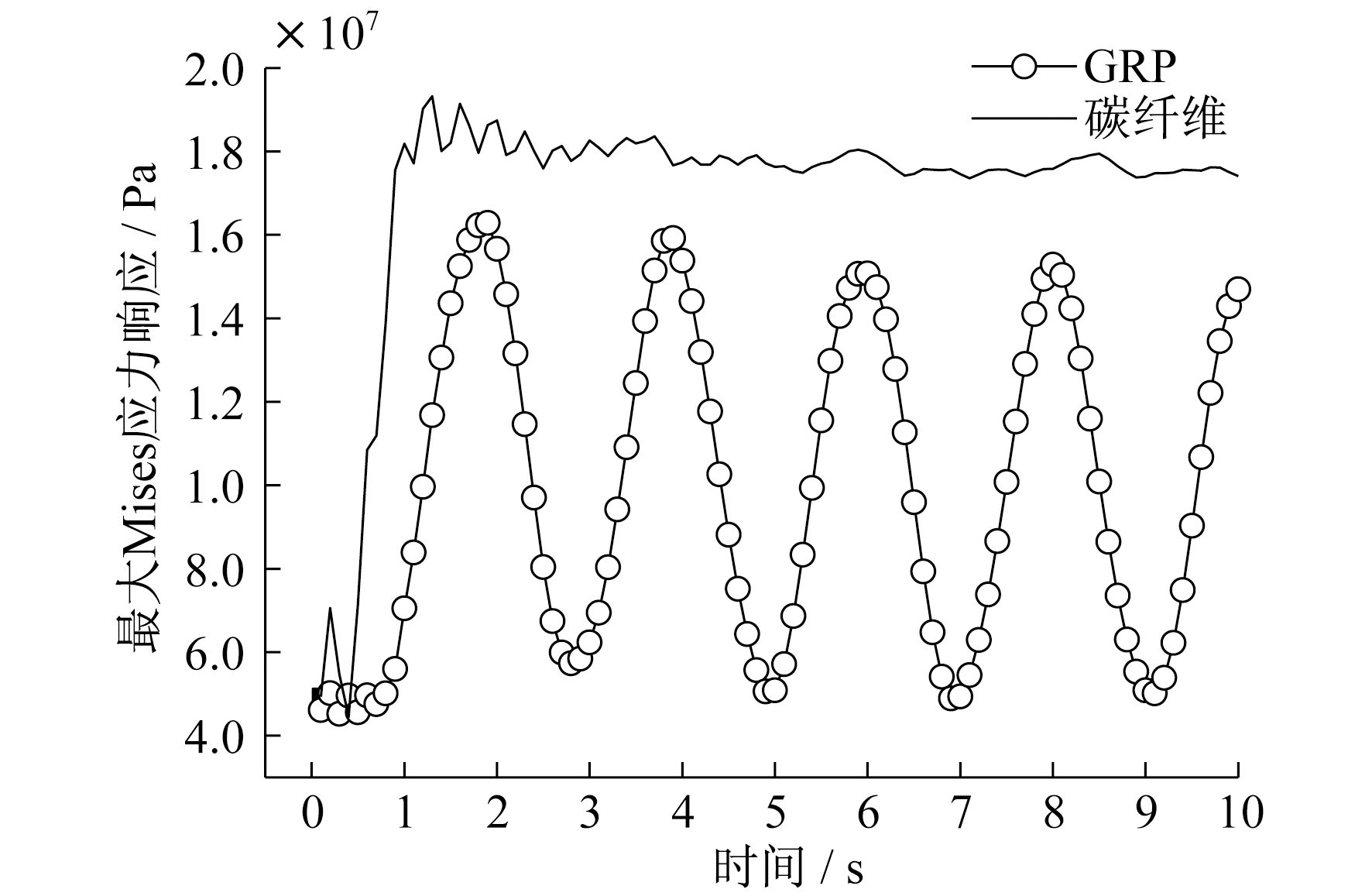
碳纤维与GRP叶片最大Mises应力响应曲线如图 4所示。由图 4可知:GRP叶片应力响应呈现明显的周期性波动, 周期约为2 s; 碳纤维叶片应力在迅速增加到1.8×10⁷Pa后保持较小的波动, 而波动周期和峰谷值均没有明显的规律; 碳纤维叶片最大Mises应力响应在1 s之后的值均大于GRP应力峰值。

图 4 碳纤维与GRP叶片最大Mises应力响应

3 结论

对比了碳纤维与GRP材料叶片在静止工况下叶片和风轮的振动模态, 得到了叶片在额定运行工况下的位移和应力, 结论如下:

(1) 两种材料叶片的各阶模态振型相同, 且仅在第十阶出现扭转振动, 说明碳纤维与GRP材料叶片均具有良好的抗扭能力;

(2) 风轮的每三阶模态频率对应于单叶片的同一阶, 但这三阶振型并不完全相同, GRP风轮部分阶次的摆振比碳纤维更明显, 表明碳纤维抗摆振能力强于GRP材料;

(3) 两种材料单叶片应力峰值均出现在叶片中部, 位移沿翼展方向逐步增大, GRP叶片振动位移远大于碳纤维材料, 而碳纤维叶片应力相对较高。

参考文献

[1]

复合材料风电叶片技术的现状与发展[J]. 新材料产业, 2010(12): 4-7. DOI:10.3969/j.issn.1008-892X.2010.12.002

[2]

基于租房客调研的家具设计要素探析[J]. 绿色科技, 2018(16): 213-215.

[3]

碳纤维增强树脂基复合材料低温贮箱抗渗漏性研究进展[J]. 玻璃钢/复合材料, 2018(11): 109-116.

[4]

国外现役潜射弹道导弹技术性能综述与分析[J]. 飞航导弹, 2018(9): 31-35.

[5]

仿昆微扑翼飞行器三维整体设计及制造[J]. 机械设计与制造, 2016(10): 107-109. DOI:10.3969/j.issn.1001-3997.2016.10.028

[6]

风力发电机叶片建模及有限元分析[J]. 上海电力学院学报, 2016, 32(3): 257-260.

[7]

QIN Z W, XU Y, YANG K, et al. Structural strength and failure prediction on FRP laminate of wind turbine blade[J]. Journal of Engineering Thermophysics, 2012, 33(4): 591-594.

[8]

DE T, CHEN G H, ZHANG J M. Finite element analysis of 5 MW fiberglass and carbon fiber wind turbine blade[J]. Advanced Materials Research, 2011, 418-420: 606-609. DOI:10.4028/www.scientific.net/AMR.418-420.606

[9]

碳纤维复合材料风力发电机叶片振动特性研究[J]. 玻璃钢/复合材料, 2018(9): 70-74.

[10]

MELTEM A K, HASAN G. A review on machinability of carbon fiber reinforced polymer(CFRP)and glass fiber reinforced polymer(GFRP)composite materials[J]. Defence Technology, 2018, 14(4): 318-326. DOI:10.1016/j.dt.2018.02.001

[11]

ZHAO Z K, DU S S, LI F, et al. Mechanical and tribological properties of short glass fiber and short carbon fiber reinforced polyethersulfone composites: a comparative study[J]. Composites Communications, 2018, 8: 1-6. DOI:10.1016/j.coco.2018.02.001

[12]

BALOKAS G, THEOTOKOGLOU E E. Cross-section analysis of wind turbine blades: comparison of failure between glass and carbon fiber[J]. Advanced Composite Materials, 2018, 27(6): 561-574. DOI:10.1080/09243046.2017.1405602

[13]

碳纤维复合材料在风力发电机叶片中的应用[J]. 电网与清洁能源, 2008(11): 53-57. DOI:10.3969/j.issn.1674-3814.2008.11.012

[14]

复合材料用高性能炭纤维的发展和应用[J]. 新型炭材料, 2000(1): 68-75. DOI:10.3321/j.issn:1007-8827.2000.01.015

[15]

宗楠楠.小型水平轴风力机叶片设计与有限元分析[D].上海: 上海交通大学, 2009.

[16]

大型风力机叶片三维建模及模态分析[J]. 太原科技大学学报, 2012, 33(3): 190-193. DOI:10.3969/j.issn.1673-2057.2012.03.006

[17]

基于水平轴风力机桨叶结冰的振动模态分析[J]. 南水北调与水利科技, 2015, 13(5): 918-921.