|
|
|
发布时间: 2019-12-10 |
|
|
|
|
收稿日期: 2018-11-28
中图法分类号: TK11
文献标识码: A
文章编号: 1006-4729(2019)06-0525-06
|
摘要
为缓解国家电网压力, 根据国家民用建筑供暖标准:GB 50736—2012, 设计了固体蓄热式供暖装置。分别开设了不同孔数的圆形或椭圆形孔道, 用数值计算的方法研究了自然对流工况下, 开设的孔数和孔形对蓄热装置放热特性的影响。结果表明:椭圆形孔道中心线及孔出口温度明显高于圆形孔道相应位置处温度; 相同孔形, 孔数越多, 孔中心温度越高, 越有利于放热; 孔数越多, 孔中心速度越小, 与孔形无关; 散热开始时, 椭圆孔出口温度高于圆孔, 但约1.4 h后, 椭圆孔出口温度开始低于圆孔, 孔数对出口温度影响不大; 圆形孔出口温度随时间的延长变化较为平缓。
关键词
固体蓄热装置; 自然对流; 孔形; 孔数
Abstract
In order to reduce the pressure of national electricity grid and responding to the off-peak electricity utilization policy:GB 50736—2012, a solid heat storage device is designed according to the national civil building heating standard.Different numbers of circular and elliptical channels are set up on the heat storage device, and by using numerical calculation to solve the project.The effects of pore shape and number on the heat storage device's heat discharge characteristics were investigated with the condition of natural convection.The results show that the temperature of the center line and the outlet temperature of the ellipse channel is obviously higher than that at the corresponding position in the circular channel.While the shape of the hole is the same, large channel numbers make the center temperature of the hole higher, thus more beneficial to heat discharge performance of solid heat storage device.The bigger the hole number is, the smaller the velocity of the center is.However, the pore shape has little effect on the center speed.At the beginning of the heat release, the outlet temperature of the elliptical hole is higher than that of the circular hole.While about 1.4 hours later, the outlet temperature of the elliptical hole begins to be lower than that of the circular hole, and the number of holes has little effect on the outlet temperature.The exit temperature of circular hole changes more slowly with time.
Key words
solid heat storage device; natural convection; pore shape; hole number
改变人类活动所需的能源结构, 因地制宜, 更多更广泛地使用风能和太阳能可再生能源, 是今后能源利用的发展方向。但由于风能和太阳能的不稳定性, 若需要大规模使用, 对储能就提出了更高的要求。近年来世界各国科学家和工程技术人员对储能的研究已越来越多[1-5]。我国冬季供暖所用能源85%以上是煤(包括热电联产)[6], 也是我国冬季雾霾频发的重要因素之一。为此目前我国主要用天然气或电来替代以煤为主要热源的供暖方式, 但我国天然气十分匮乏, 且大量燃烧天然气会排放较多的氮氧化物。据统计, 目前大部分天然气锅炉氮氧化物排放浓度约在300 mg/m3。此外, 限制煤改气实施最为重要的一点就是安全问题。电是理想的替代方式之一, 但目前我国发电用煤的比例还较高, 火电厂排放的污染物在大气污染中占相当的比例, 而且采用电取暖无疑会对火电机组备用提出更高的要求。因此, 在用电供热的场合, 使用电蓄热装置, 将用电低谷时的电转换成热储存起来, 在用电高峰时放出, 这样既可以有效缓解发电系统的供需矛盾, 又可以使用户利用峰谷差电价降低用电成本。固体蓄热装置结构简单、安全可靠、成本低, 得到了工程技术人员的重视, 目前市场上供暖产品大多采用的是固体蓄热装置。
为提高固体蓄热装置的热利用效率, 其放热特性的研究就显得十分重要, 但目前这方面的研究还很少。胡恩科等人[7-8]在强制对流工况下, 采用标准k-ε模型, 用数值计算的方法模拟了固体蓄热装置上分别开有圆孔和椭圆孔时, 固体蓄热装置的放热特性。研究结果表明, 对于氧化镁固体材料, 圆孔开始放热时, 孔数越多, 出口温度越高, 约2.8 h后, 孔数越多, 出口温度越低; 随着放热时间的延长, 孔数越多, 出口温度下降越快, 出口速度也基本有同样规律, 变换的临界时间约是放热开始后2.6 h。此外, 椭圆孔出口温度变化规律与圆孔相同, 当孔数达到64个时, 椭圆孔内的温度明显高于圆孔内温度。杨志刚[9]采用470 mm×90 mm×580 mm的氧化镁蓄热砖, 在分别开缝为5 mm, 10 mm, 15 mm的自然对流工况下, 进行了试验研究, 结果表明, 开缝可以提高蓄热体放热效率。赵广播等人[10]在强制对流工况下, 对环形腔内充满固体蓄热粒子并加装12根金属散热管的装置进行了放热特性研究, 结果表明, 不同位置的散热管其放热效率不同, 最大相差达70%。
已有的研究结果表明, 若将蓄热装置作为家庭或建筑物中的取暖设备, 其自然对流换热特性非常重要, 而蓄热体是否开孔, 孔形状、数量等对蓄热体散热均有十分重要的影响。本文根据GB 50736—2012《民用建筑供暖通风与空气调节设计规范》[11]与ASTM-C16.30标准[12], 设计了蓄热装置, 利用数值模拟方法, 研究了自然对流工况下, 圆形和椭圆形孔道及孔道数量对固体蓄热装置放热特性的影响, 以期为相关工程技术人员及固体蓄热装置的使用提供参考。
1 固体蓄热装置放热特性模型建立
1.1 物理模型
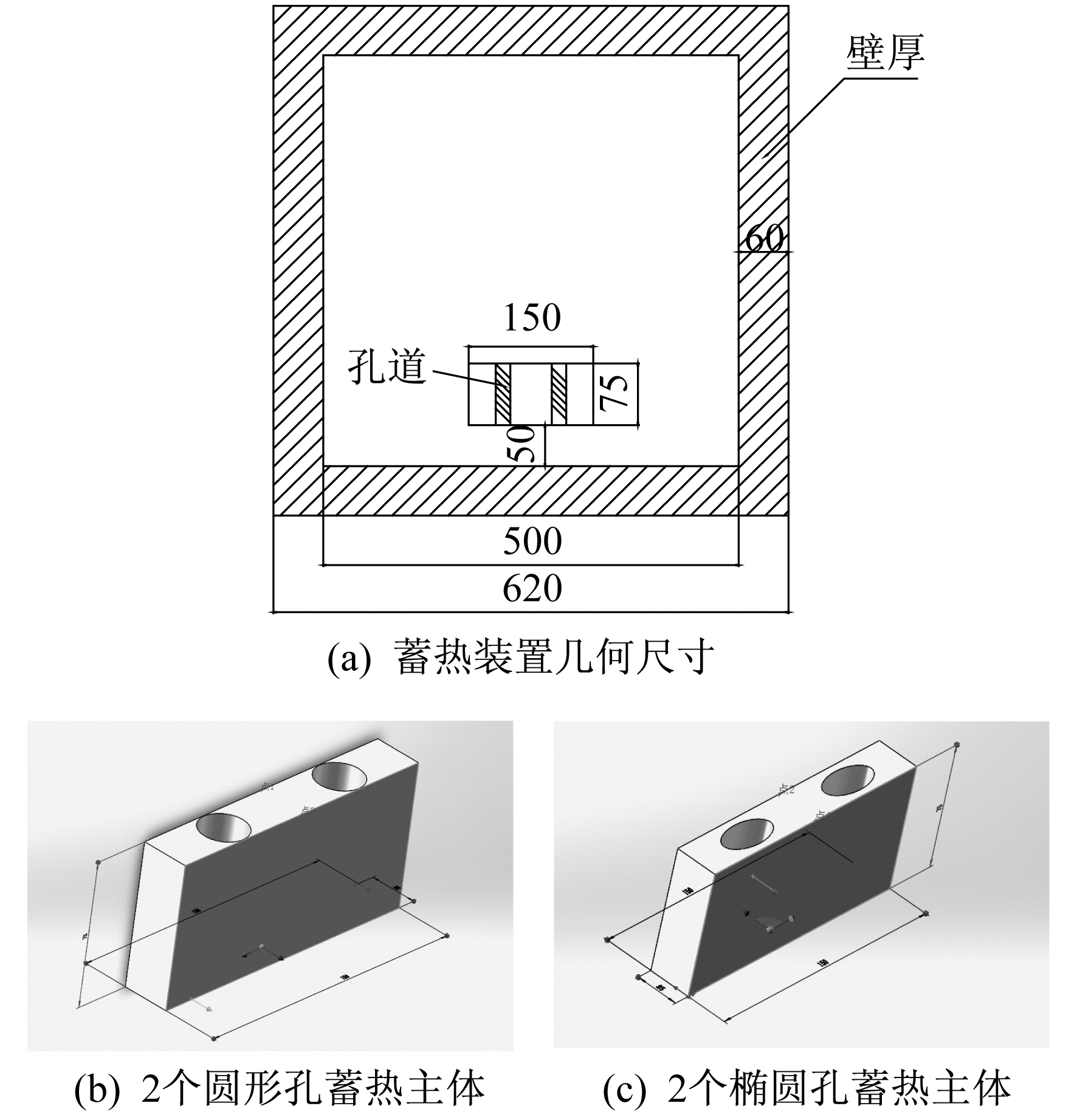
根据GB 50736—2012和ASTM-C16.30标准, 本文设计的蓄热装置尺寸如下:蓄热体长宽高分别为150 mm×25 mm×75 mm, 正方体框边长为500 mm, 壁厚为60 mm。
蓄热体置于靠墙100 mm、距地面50 mm的位置。蓄热体材料为镁砖, 壁厚材料为发泡水泥保温材料, 正方体中介质为空气。表 1为蓄热材料的物性参数。
表 1
几种蓄热材料物性参数
| 蓄热 材料 |
密度ρ/ (kg· m-3) |
比热容 Cp/ [J·(kg· K-1)] |
导热系数 λ/[W· (m· K)-1] |
热容量 Q/[kJ· (m3· K)-1] |
热扩散率a/(m2· s-1) |
| 氧化镁 | 3 000 | 1 000 | 4.5~6 | 3 000.0 | (1.5~2)× 10-3 |
| 保温 材料 |
450 | 1 164 | 0.085 | 523.8 | 1.62×10-7 |
本文共计算了孔形为圆形和椭圆形、孔道数量为2个和8个的4种模型。图 1给出圆形和椭圆形孔道数量为2个的蓄热体形状示意图。
1.2 数学模型
该蓄热体放热过程是一个具有内热源的非稳态传热过程, 满足的连续性方程、动量方程及能量方程如下。
连续性方程为
| $ \frac{\partial \rho}{\partial t}+\frac{\partial \rho u}{\partial x}+\frac{\partial \rho v}{\partial y}+\frac{\partial \rho z}{\partial z}=0 $ | (1) |
式中:ρ——密度;
u——速度矢量;
t——时间。
动量方程为
| $ \begin{aligned} \frac{\partial \rho u}{\partial t}+\operatorname{div}(\rho u u)=&-\frac{\partial p}{\partial x}+\frac{\partial \tau_{x x}}{\partial x}+\\ & \frac{\partial \tau_{y x}}{\partial y}+\frac{\partial \tau_{z x}}{\partial z} \\ \frac{\partial \rho v}{\partial t}+\operatorname{div}(\rho v u)=&-\frac{\partial p}{\partial y}+\frac{\partial \tau_{x y}}{\partial x}+\\ & \frac{\partial \tau_{y y}}{\partial y}+\frac{\partial \tau_{z y}}{\partial z} \\ \frac{\partial \rho w}{\partial t}+\operatorname{div}(\rho w u)=&-\frac{\partial p}{\partial z}+\frac{\partial \tau_{x z}}{\partial x}+\\ & \frac{\partial \tau_{y z}}{\partial y}+\frac{\partial \tau_{z z}}{\partial z}-\rho g \end{aligned}$ | (2) |
式中:p——流体在微元体上的压力;
τxx, τxy, τxz——因分子粘性作用而产生的作用在微元体表面上的黏性应力τ的分量;
g——重力加速度。
能量方程为
| $ \frac{\partial(\rho T)}{\partial t}+d i v(\rho u T)=\operatorname{div}\left(\frac{\lambda}{C_{\mathrm{p}}} \cdot \operatorname{grad} T\right)+S_{T} $ | (3) |
式中:T——热力学温度;
λ——流体的导热系数;
Cp——比热容;
ST——黏性耗散量。
由于房间空气密度、导热系数、比热容、黏度等均随温度的变化而变化, 因此对在一个标准大气压下干空气热物理参数测试得到的数据进行了拟合[13]。其具体表达式如表 2所示。
表 2
空气物性参数表达式
| 名称 | 表达式 |
| 密度 | $\rho=1.0 \times 10^{5} T^{2}-0.0116 T+3.5152$ |
| 导热系数 | $\lambda=8.0 \times 10^{8} T^{2}+0.0001 T-0.0037$ |
| 比热容 | $C_{\mathrm{p}}=2.4 \times 10^{3} T^{2}-1.4691 T+1226.8$ |
| 漆度 | $v=4.0 \times 10^{11} T^{2}+3.0 \times 10^{8} T+7.0 \times 10^{6}$ |
| 注: T-温度, $\mathrm{K}_{\circ}$ | |
1.3 数值模拟条件及参数设定
2 数值模拟结果分析
为了便于分析比较, 在计算过程中, 固体蓄热体体积保持不变, 为2.10×10-4m3。蓄热体总横截面积为3.75×10-3 m2, 其中孔道总横截面积和固体总横截面积分别为2.812 5×10-3m2和9.375 0×10-4m2。不论何种孔型, 孔数相同单孔表面积相同, 其换热面积就相同, 如表 3所示。
表 3
不同孔数下的圆形、椭圆形孔道几何参数
| 孔形 | 孔数 | 单孔横 截面积/ 10-4m2 |
单孔半径/ m |
单孔表 面积/ 10-4m2 |
多孔总 表面积/ 10-2m2 |
| 圆形 | 2 | 4.7 | 0.012 2 | 5.745 0 | 1.149 |
| 8 | 1.2 | 0.006 1 | 2.872 5 | 2.298 | |
| 椭圆 | 2 | 4.7 | 0.008 6 | 6.632 7 | 1.327 |
| 8 | 1.2 | 0.004 4 | 3.363 5 | 2.691 | |
| 注:表中椭圆单孔半径栏中的数据为椭圆短轴长度, 孔数为2和8的椭圆孔的长轴长分别为0.017 2 m和0.008 7 m。 | |||||
2.1 孔形和孔数对孔道内温度的影响
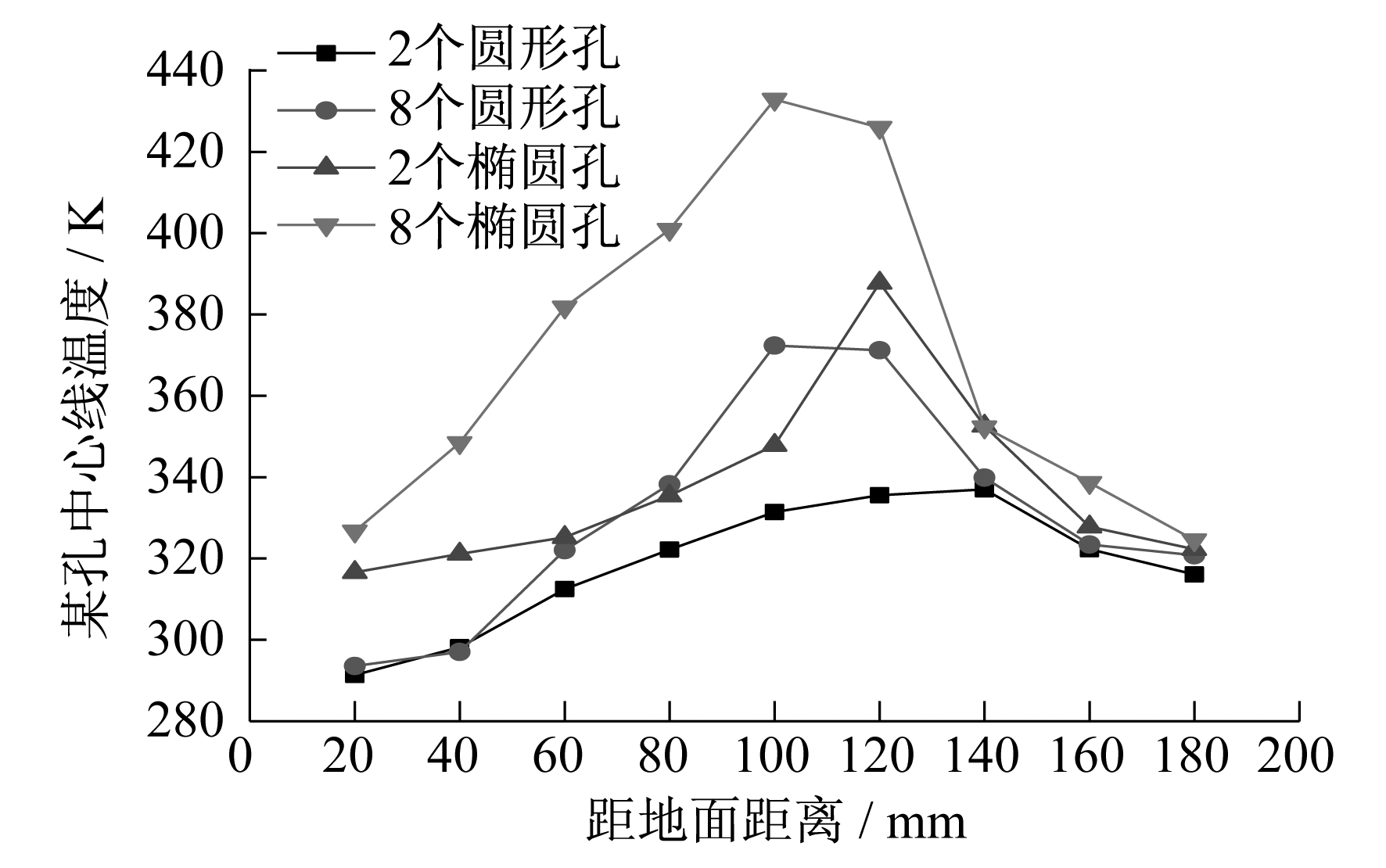
图 2给出了孔形和孔数对孔道内温度的影响。横坐标为孔道中心线各点温度距地面的距离。
由图 2可以看出, 椭圆孔中心线温度基本上高于圆形孔同样位置的温度, 即使在蓄热体外(横坐标小于50 mm和大于125 mm的区域)也是如此, 两者差别的最大处位于距离孔上方出口约10 mm处。同样孔数条件下, 椭圆孔较圆孔温度高了约17%, 但在蓄热体外, 两者的差别在减小。这是因为当单孔横截面积相等时, 椭圆的周长大于圆形周长, 因此椭圆孔向孔道传热的换热面积大于圆形孔的换热面积, 其换热量也较大, 使得孔中心温度较高。此外, 相同孔形, 孔数越多, 其孔中心温度越高。椭圆孔这种现象更加明显。这是因为在相同孔形工况下, 要保持孔道总横截面积相同, 孔数越多, 其当量直径越小, 孔中心线越接近蓄热体, 因此温度也越高。
2.2 孔形和孔数对孔道内速度的影响
孔形和孔数对孔道内速度的影响如图 3所示。
由图 3可以看出, 不论孔数多少, 椭圆孔内中心线速度均大于圆形孔; 相同孔数工况下, 椭圆孔内速度较圆孔内速度要大30%左右。这与相同孔数下椭圆孔中心温度较高有关(见图 2)。在自然对流工况下, 温度越高, 分子热运动越剧烈, 速度也越快。无论何种孔形和孔数, 距地面约40 mm处, 空气速度开始增加, 进入孔道后(横坐标为50 mm), 速度迅速增加, 到达一定值后, 速度保持不变, 椭圆孔在距蓄热体出口约25 mm处(横坐标125 mm为蓄热体出口), 圆孔在距蓄热体出口约15 mm处速度开始下降, 这是受到孔出口效应影响所致。
由图 3还可以看出, 孔中心线速度在离开蓄热体出口约15 mm处速度有个最小值, 是由孔出口与出口附近旋涡效应共同作用的结果[16]。孔形相同时, 孔数越多, 中心线速度越小。因为当孔形相同时, 若保持孔横截面积不变, 则孔数越多, 孔的当量直径越小, 在自然对流工况下, 其空气阻力也越大, 致使速度较小。
2.3 孔道内空气换热量的变化
在自然对流工况下, 当蓄热体上有孔时, 该孔已成为蓄热体散热的一部分, 因此孔出口温度、孔形、孔数及孔轴的方向等对整个蓄热体散热均有影响。根据能量方程, 孔散热量可表示为
| $\Phi=q_{\mathrm{m}^{\prime \prime}} C_{\mathrm{p}^{\prime \prime}} t_{\mathrm{f}^{\prime \prime}}-q_{\mathrm{m}^{\prime}} C_{\mathrm{p}^{\prime}} t_{\mathrm{f}^{\prime}}$ | (4) |
式中:qm′, qm″——空气进出口的质量流量, kg/m3;
Cp′, Cp″——空气进出口的比热容;
tf′, tf″——孔道进出口空气温度, K。
由于空气密度、比热容和温度都随时间的变化而变化, 这里选取时间为1.0×104 s时的数据代入表 2拟合公式计算瞬时值, 从而求出孔道换热量进行分析比较。
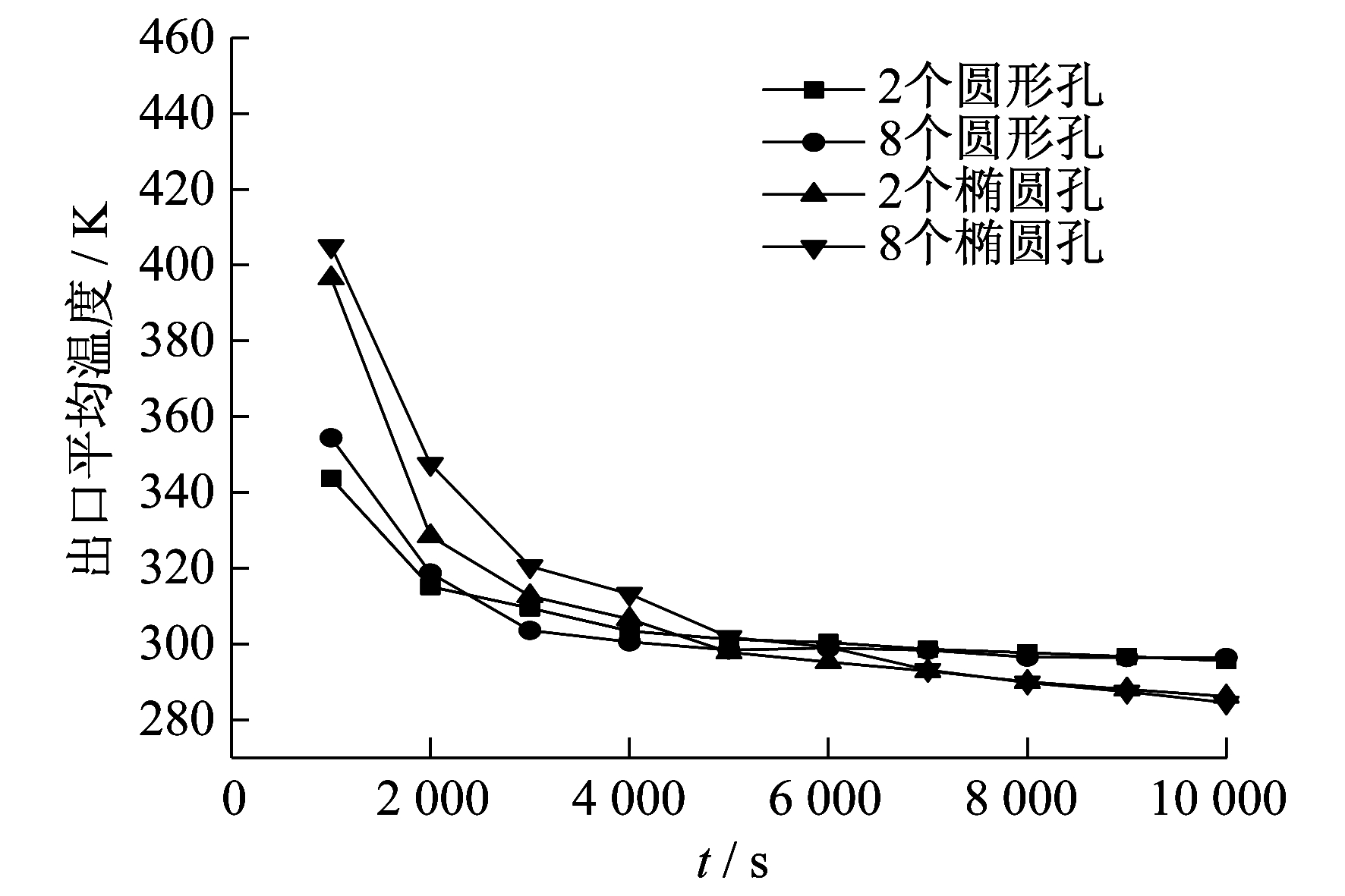
孔形和孔数对孔出口平均温度的影响如图 4所示。
由图 4可以看出, 开始时, 椭圆孔出口温度高于圆孔, 但在5 000 s(约1.4 h)左右时, 椭圆孔出口温度开始低于圆孔, 而在本文计算工况下, 孔数对出口温度影响不大。圆形孔出口温度随时间延长变化较平缓。
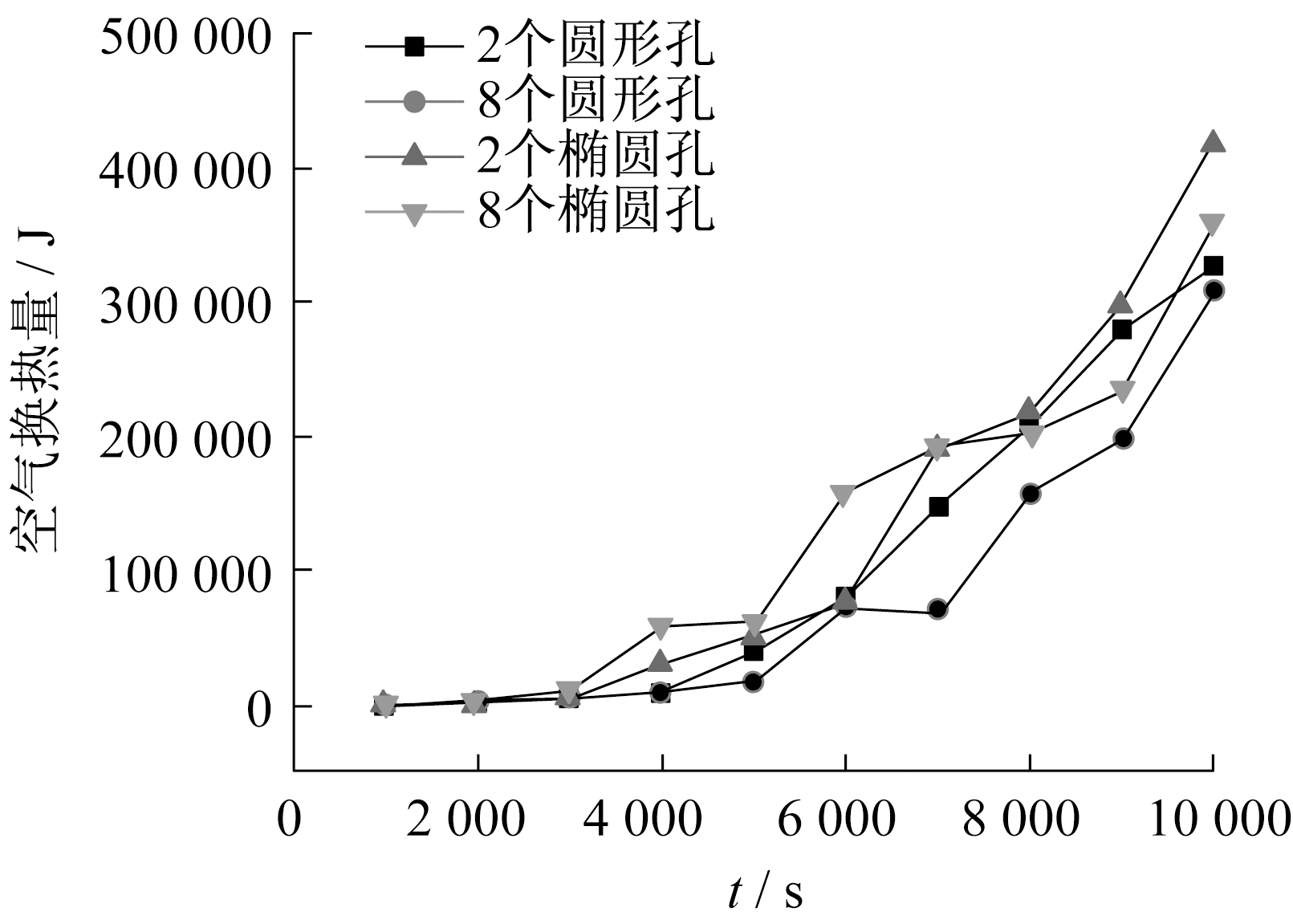
孔道内空气换热量随时间变化如图 5所示。
由图 5可以看出, 通过孔向计算空间的散热量时, 开始基本不变, 但在5 000 s左右时, 散热量开始急剧增加, 而孔形和孔数均对此无太大影响。
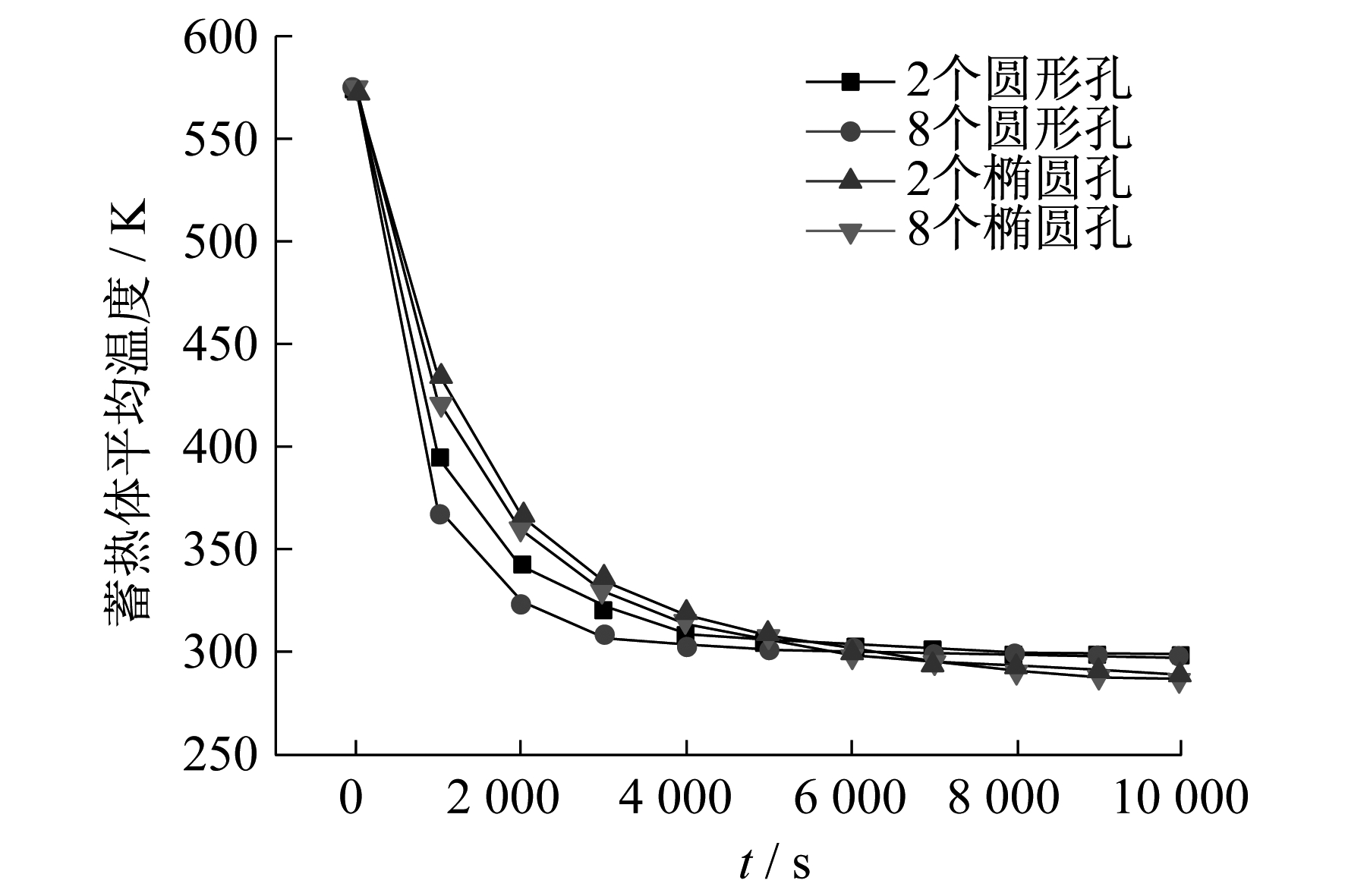
2.4 蓄热体平均温度的变化
3 结论
(1) 在计算工况下即固体蓄热体体积保持不变、蓄热体总横截面积一定时, 椭圆孔道中心温度明显高于圆孔道中心线温度, 最大相差17%左右。在蓄热体外(孔中心线的延长线)也有这种现象, 但两者的差别有所减小。相同孔形下, 孔数越多, 其孔中心温度越高, 对椭圆孔尤为明显。
(2) 不论孔数多少, 椭圆孔内中心线速度均大于圆孔。相同孔数下, 椭圆孔内速度较圆孔内速度要大30%左右。
(3) 不论何种孔形和孔数, 距地面约40 mm处, 空气速度开始增加, 进入孔道后, 速度迅速增加, 到达一定值后, 速度保持不变; 椭圆孔在距蓄热体出口25 mm左右、圆孔在距蓄热体出口15 mm左右速度开始下降。同一种孔形, 孔数越多, 孔中心速度越小。
(4) 散热开始时, 椭圆孔出口温度高于圆孔, 但在5 000 s(约1.4 h)左右时, 椭圆孔出口温度开始低于圆孔, 而在本文计算工况下, 孔数对出口温度影响不大。圆孔出口温度随时间的延长变化较为平缓。
(5) 通过孔向计算工况空间的散热量时, 开始基本不变, 但在5 000 s左右时, 散热量开始急剧增加, 孔形和孔数均对此无太大影响。散热开始时, 椭圆孔蓄热体平均温度下降较圆孔的蓄势体平均温度慢, 但在5 000 s后, 椭圆孔较圆孔下降得快, 孔数越多这种现象越明显。
参考文献
-
[1]高温蓄热技术的研究现状及展望[J]. 建筑节能, 2011(9): 32-38. DOI:10.3969/j.issn.1673-7237.2011.09.009
-
[2]纳米碳/氢氧化锂复合材料的低温化学蓄热性能研究[J]. 工程热物理学报, 2016, 37(12): 2512-2516.
-
[3]太阳能热泵相变蓄热供暖系统参数影响研究[J]. 太阳能学报, 2015, 36(8): 2028-2035. DOI:10.3969/j.issn.0254-0096.2015.08.038
-
[4]太阳能热发电的显热蓄热技术进展[J]. 可再生能源, 2014, 32(7): 901-905.
-
[5]组合式高温相变蓄热器蓄热过程的数值模拟[J]. 可再生能源, 2016, 34(1): 106-111.
-
[6]北方城市清洁供暖现状和技术路线研究[J]. 区域供热, 2018(1): 11-18.
-
[7]固体蓄热装置的蓄、放热特性数值模拟分析[J]. 流体机械, 2014, 42(8): 78-83. DOI:10.3969/j.issn.1005-0329.2014.08.017
-
[8]圆形和椭圆形孔道固体蓄热装置蓄放热特性模拟[J]. 热力发电, 2018(1): 38-45.
-
[9]杨志刚.高温显热蓄热式电暖气的研制及其传热性能研究[D].北京: 北京工业大学, 2005.
-
[10]电热固体蓄热装置放热过程的实验研究[J]. 电站系统工程, 2003, 19(6): 13-14. DOI:10.3969/j.issn.1005-006X.2003.06.005
-
[11]中国建筑科学研究院.民用建筑供暖通风与空气调节设计规范: GB 50736—2012[S].北京: 中国建筑工业出版社, 2012.
-
[12]FEUILLOLEY P, ISSANCHOU G. Greenhouse covering materials measurement and modelling of thermal properties using the hot box method, and condensation effects[J]. Journal of Agricultural Engineering Research, 1996, 65(2): 129-142. DOI:10.1006/jaer.1996.0085
-
[13]杨世铭, 陶文铨.传热学[M]. 4版.北京: 高等教育出版社, 2006.
-
[14]温正. FLUENT流体计算应用教程[M].北京: 清华大学出版社, 2013.
-
[15]采用不同辐射换热模型对液氦传输管线的数值研究[J]. 低温与超导, 2015, 43(11): 26-29.
-
[16]贾月梅.流体力学[M].北京: 国防工业出版社, 2006.