|
|
|
发布时间: 2019-12-10 |
|
|
|
|
收稿日期: 2018-09-13
基金项目: 国家自然科学基金(51277119)
中图法分类号: TM71
文献标识码: A
文章编号: 1006-4729(2019)06-0518-07
|
摘要
基于机会约束规划的随机最优潮流模型的求解一般采用智能优化算法, 提出了一种内点法结合随机调节因子更新的方法, 以求解基于机会约束规划的含风电场电力系统的随机最优调度模型。模型考虑了节点电压和线路功率的机会约束, 并采用半不变量和Cornish-Fisher级数结合的方法来计算机会约束的概率分布。引入调节因子, 对机会约束概率进行变形, 将随机最优潮流问题转化为可采用内点法求解的最优潮流模型。提出了调节因子的更新方法, 通过原始对偶内点法的参数结果更新调节因子来调节机会约束满足的概率, 迭代求解机会约束随机最优潮流模型。最后, 以IEEE14和IEEE118节点系统为例, 验证了方法的正确性和有效性。
关键词
随机最优潮流; 风力发电; 内点法
Abstract
The stochastic optimal power flow (SOPF) is usually solved based on intelligent optimization algorithm.The update algorithm of the regulatory variables in the interior point method is proposed for the SOPF model of power system including wind power.The stochastic inputs and chance constraints are modeled based on cumulants and Cornish-Fisher series.The regulatory variables are proposed to divide the chance constrained stochastic optimal power flow into a deterministic optimal power flow (DOPF) model.The regulatory variables are updated iteratively according to the stochastic inputs and optimal solution solved by primal-dual interior point method (PDIPM).The results on IEEE14 and IEEE18 systems with wind farms verify the feasibility and effectiveness of the proposed algorithm.
Key words
stochastic optimal power flow; wind power; interior point method
在可再生能源领域, 风力发电因成本较低、技术成熟、可靠性较高, 得到了大规模发展, 而大规模并网风力发电的随机性给电力系统的经济调度和安全运行带来极大的挑战[1]。在大规模风电场并网的背景下, 研究含随机因素的最优潮流具有重要意义[2-6]。风电功率的随机波动极有可能导致实时调度或控制时出现线路功率阻塞或节点电压过高等现象, 而采用考虑随机因素最优潮流模型的调度方案对随机因素具有耐受性, 可预防风电功率波动对电网的影响。
机会约束规划作为解决含随机变量的随机优化方法, 近年来在电力系统领域得到应用。文献[7]引入机会约束规划, 计算并网风电场的最大注入功率, 并应用混合智能算法求解优化模型。文献[8]在机会约束规划的框架下确定了系统所需的最优旋转备用容量, 并采用基于蒙特卡洛仿真的遗传算法进行求解。文献[9]建立了含风电场的随机动态最优潮流, 采用随机模拟的混合智能技术来求解随机规划模型。文献[10]结合采样平均技术和遗传算法, 求解考虑随机因素的机组组合问题。文献[11]基于机会约束模型研究了分布式电源的位置和容量优化问题, 并采用Monte-Carlo抽样法和遗传算法相结合的方法进行求解。这些问题的求解过程中都需要最优潮流计算作为工具。
现有的文献中, 基于机会约束规划的随机最优潮流(Stochastic Optimal Power Flow, SOPF)模型的求解一般采用智能优化算法[11]。对于含风电场的电力系统随机最优潮流, 采用智能算法进行求解时, 计算量较大。文献[12]中提出的改进原始对偶内点法可以求解目标函数分段可微的电力系统最优潮流计算问题, 具有较快的计算速度和良好的收敛性。本文在文献[12]中内点法的基础上, 加入与随机因素相关的调节因子, 将随机规划问题转化为确定的非线性优化问题, 迭代求解含风电的随机调度模型, 并通过算例分析进行验证。
1 随机最优潮流模型
1.1 模型的建立
以发电机组报价之和最小为目标, 则目标函数的公式为
| $ f=\sum_\limits{i \in C_{\mathrm{G}}}\left(C_{2, i} P_{\mathrm{G}i}^{2}+C_{1, i} P_{\mathrm{G}i}+C_{0, i}\right) $ | (1) |
式中:CG——可调节发电机的集合;
C2, i, C1, i, C0, i——节点i的发电成本的相关系数;
PGi——节点i的发电机有功功率。
等式约束条件为
| $ \left\{\begin{array}{c} P_{\mathrm{G}i}+P_{\mathrm{W}i}-P_{\mathrm{D}i}-U_{i} \sum\limits_{j=1}^{n} U_{j}\left(G_{i j} \cos \theta_{i j}+\right. \\ \left.B_{i j} \sin \theta_{i j}\right)=0 \\ Q_{\mathrm{G}i}+Q_{\mathrm{W} i}-Q_{\mathrm{D}i}+U_{i} \sum\limits_{j=1}^{n} U_{j}\left(G_{i j} \sin \theta_{i j}-\right. \\ \left.B_{i j} \cos \theta_{i j}\right)=0 \end{array}\right. $ | (2) |
式中:PWi, QWi——风电场的有功功率和无功功率;
PDi, QDi——负荷的有功功率和无功功率;
Ui, Uj——节点i和j的电压幅值;
Gij, Bij——节点i和j间的互导纳;
θij——节点i和j间的相角差;
QGi——节点i处发电机的无功功率。
不等式约束条件为
| $ P_{\mathrm{G}i}^{\min } \leqslant P_{\mathrm{G}i} \leqslant P_{\mathrm{G}i}^{\max } $ | (3) |
| $ Q_{\mathrm{G}i}^{\min } \leqslant Q_{\mathrm{G}i} \leqslant Q_{\mathrm{G}i}^{\max } $ | (4) |
其中,
| $ P_{\mathrm{G}i}^{\max }=\min \left\{P_{{\mathrm{G}i}, \max }, P_{{\mathrm{G}i}}^{\prime}+U_{\mathrm{up}}\right\} $ |
| $ P_{\mathrm{G}i}^{\min }=\max \left\{P_{\mathrm{G}i, \min }, P_{\mathrm{G}i}^{\prime}-D_{\mathrm{d o}}\right\} $ |
式中:PGi, max——机组最大调度出力;
P′Gi——前一时刻的机组出力;
Uup——有功出力上升速率;
PGi, min——机组最小调度出力;
Ddo——有功出力下降速率。
机会约束条件为
| $ P\left(U_{i} \geqslant U_{i}^{\min }\right) \geqslant \beta_\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{{v_{i}}} $ | (5) |
| $P\left(U_{i} \leqslant U_{i}^{\max }\right) \geqslant \beta_{v_{i}}^{-}$ | (6) |
| $ P\left(S_{ij} \geqslant S_{ij}^{\min }\right) \geqslant \beta_\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{{S_{ij}}} $ | (7) |
| $P\left(S_{i j} \leqslant S_{i j}^{\max }\right) \geqslant \beta_{\overline{S_{i j}}}$ | (8) |
式中:P(·)——不等式成立的概率值;
βi——一组事先给定的置信水平, 其大小反映了电力系统运行水平要求, βi∈[0, 1]。
1.2 随机因素
考虑负荷和风电场的功率波动, 其公式分别为
| $ P_{\mathrm{D}}=P_{\mathrm{D}}^{\mathrm{d}}+P_{\mathrm{D}}^{\mathrm{e}}, P_{\mathrm{D}}^{\mathrm{e}} \sim N\left(a, b^{2}\right) $ | (9) |
| $ P_{\mathrm{W}}=P_{\mathrm{W}}^{\mathrm{d}}+P_{\mathrm{W}}^{\mathrm{e}} $ | (10) |
式中:PD——负荷功率实际值;
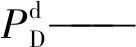 负荷功率预测值;
负荷功率预测值;
 负荷功率实际值与预测值之差;
负荷功率实际值与预测值之差;
PW——风电场的输出功率;
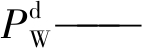 风电场输出功率的预测值;
风电场输出功率的预测值;
 风电场实际输出功率与预测值之差。
风电场实际输出功率与预测值之差。
由于负荷和风电功率的计算是采用不同的预测方法, 故认为预测误差相互独立。负荷的预测误差满足正态分布, 风电功率的预测误差采用半不变量和Cornish-Fisher级数[13-14]表示为
| $ \begin{aligned} f(x)=& \phi(x)+\frac{1}{6}\left[\phi^{2}(x)-1\right] c_{3}+\\ & \frac{1}{24}\left[\phi^{3}(x)-3 \phi(x)\right] c_{4}-\\ & \frac{1}{36}\left[2 \phi^{3}(x)-5 \phi(x)\right] c_{3}^{2}+\\ & \frac{1}{120}\left[\phi^{4}(x)-6 \phi^{2}(x)+3\right] c_{5}+\cdots \end{aligned} $ | (11) |
式中:φ(x)——标准正态分布的概率密度函数;
ci——i阶规格化后的半不变量, 可通过统计实际风电功率预测误差得到,
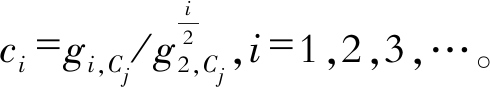
2 基于内点法的随机最优潮流模型求解
2.1 基于调节因子的随机模型转化
总结式(1)~式(8), 得到机会约束下的随机最优潮流模型为
| $ \begin{array}{ll} \min & f(X) \\ & G(X)=0 \\ \mathrm{s}. \mathrm{t}. & H(X) \leqslant 0 \\ & P\{C(X) \leqslant 0\} \geqslant \beta \end{array} $ | (12) |
式中:X=[PG, QG, θ, V]。
求解式(12)的难点在于机会约束的处理。通过增加调节因子, 可将随机最优潮流模型转化为确定性优化问题。因此, 式(12)中的机会约束可变为
| $C(X) \leqslant a$ | (13) |
式中:a——调节因子。
a表示随机因素对确定性优化问题的影响程度, 也是随机因素和确定性表达的联系变量, a中的元素均大于等于零。由式(13)可以看出, a的取值反映了解空间的压缩程度。
根据式(12)和式(13)可得优化模型的改进拉格朗日函数为
| $ \begin{aligned} L(X, Z, \lambda, \mu)=& f(X)+\lambda^{\mathrm{T}} G(X)+\mu_{\mathrm{H}}^{\mathrm{T}}(H(X)+\\ & \left.Z_{\mathrm{H}}\right)+\mu_{\mathrm{C}}^{\mathrm{T}}\left(C(X)+Z_{\mathrm{C}}-a\right)-\\ & \gamma \sum_{m=1}^{n_{i}} \ln \left(Z_{m}\right) \end{aligned} $ | (14) |
式中:λ——等式约束的拉格朗日乘子;
μH, μC——不等式约束的拉格朗日乘子;
γ——扰动因子;
ZH, ZC——不等式约束的松弛因子;
Zm——松弛变量, Zm > 0。
式(14)对应的KKT条件为
| $ \left\{\begin{array}{l} f_{X}+\lambda^{\mathrm{T}} G_{X}+\mu_{\mathrm{H}}^{\mathrm{T}} H_{X}+\mu_{\mathrm{C}}^{\mathrm{T}} C_{X}=0 \\ \mu-\gamma \mathrm{e}[Z]^{-1}=0 \\ G(X)=0 \\ H(X)+Z_{\mathrm{H}}=0 \\ C(X)+Z_{\mathrm{C}}-a=0 \end{array}\right. $ | (15) |
式中:fX=∂f/∂X;
GX=∂G/∂X;
HX=∂H/∂X;
CX=∂C/∂X;
μ=[μH; μC];
Z=[ZH; ZC]。
2.2 调节因子的更新
状态变量ΔX′和功率波动量的关系如下
| $\Delta X^{\prime}=J^{-1} \Delta W$ | (16) |
式中:ΔX′=[Δθ, ΔV];
J——雅克比增广矩阵;
ΔW——负荷和风力发电机的功率预测误差。
不等式约束的波动量和ΔW的关系如下
| $\Delta C=\left(C_{X} \cdot J^{-1}\right) \Delta W$ | (17) |
式中:ΔC——C(X)的波动量。
ΔCj的第i阶半不变量的计算式为
| $ g_{i, \Delta C_{j}}=\sum\limits_{j=1}^{n}\left(M_{i, j}\right)^{i} \cdot g_{i, \Delta W_{j}} $ | (18) |
式中:gi, ΔCj——ΔC的第j个元素的第i阶半不变量;
i——半不变量的阶数, i=1, 2, 3, …, N;
M=CX·J-1, 其元素为Mi, j;
N——ΔW的元素个数;
gi, ΔWj——ΔW的第j个元素的第i阶半不变量。
随机变量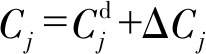 的各阶半不变量为
的各阶半不变量为
| $ g_{i, C_{j}}=\left\{\begin{array}{ll} g_{i, \Delta C_{j}}+C_{j}^{\mathrm{d}} & i=1 \\ g_{i, \Delta C_{j}} & i \neq 1 \end{array}\right. $ | (19) |
将式(19)代入式(11), 可得到Cj的概率密度函数fCj, k(c)。根据如下等价关系
| $ P\left\{C_{j} \leqslant 0\right\} \geqslant \beta_{j} \Leftrightarrow\left\{\begin{array}{l} \int_{-\infty}^{p_{j}} f_{C_{j}, k}(c) \mathrm{d} c=\beta_{j} \\ p_{j} \leqslant 0 \end{array}\right. $ | (20) |
式中:pj——满足P{Cj≤0}=βj的分位点。
当P{Cj≤0}=βj时:pj=0; pj > 0表示概率越限, 即不满足机会约束; pj≤0表示满足机会约束。
定义越界数列hβ为
| $ h_{\beta, j}=\left\{\begin{array}{ll} p_{j}, & p_{j} \gt 0 \\ 0, & p_{j} \leqslant 0 \end{array}\right. $ | (21) |
根据最优化原理, 对优化结果起作用的机会约束对应的拉格朗日乘子μC, i满足μC, i≥0。在最优点处, 有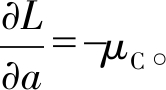 因此, 本文每一次迭代中采用式(22)更新调节因子
因此, 本文每一次迭代中采用式(22)更新调节因子
| $ a=\rho \cdot \frac{\mu_{\mathrm{C}}}{\left\|\mu_{\mathrm{C}}\right\|_{2}} \cdot h_{\beta} $ | (22) |
式中:ρ——比例因子, 取ρ=0.5。
2.3 计算流程
根据式(15)和式(22), 设定初始值k=0, a=0, 则式(12)的求解流程如下。
步骤1 k=k+1, 按照下列公式计算优化变量
| $ \begin{array}{l} X \leftarrow X+\alpha_{\mathrm{p}} \Delta X \\ Z \leftarrow Z+\alpha_{\mathrm{p}} \Delta Z \\ \lambda \leftarrow \lambda+\alpha_{\mathrm{d}} \Delta \lambda \\ \mu \leftarrow \mu+\alpha_{\mathrm{d}} \Delta \mu \\ \gamma \leftarrow \frac{\delta\left(\mu^{\mathrm{T}} Z\right)}{n i} \end{array} $ |
其中, ΔX, ΔZ, Δλ, Δμ的计算过程及符号意义参考文献[12]。加入a后, 改进计算过程如下
| $\left[\begin{array}{l}\Delta X \\ \Delta \lambda\end{array}\right]=-\left[\begin{array}{cc}M & G_{X}^{\mathrm{T}} \\ G_{X} & 0\end{array}\right]^{-1}\left[\begin{array}{c}N \\ G(X)\end{array}\right]$ |
ΔZ=-[H(X); C(X)]-Z-a-[HX; CX]ΔX
Δμ=-μ+[Z]-1(γe-[μ]ΔZ)
| $\alpha_{\mathrm{p}}=\min \left(\xi \mathop {\min }\limits_{\Delta {Z_m} < 0} \left(-\frac{Z_{m}}{\Delta Z_{m}}\right), 1\right)$ |
| $\alpha_{\mathrm{d}}=\min \left(\xi \mathop {\min }\limits_{\Delta {\mu_m} < 0} \left(-\frac{\mu_{m}}{\Delta \mu_{m}}\right), 1\right)$ |
其中,
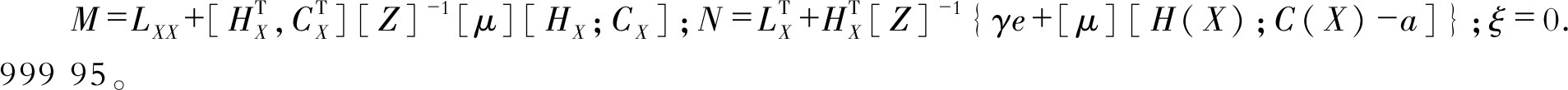
步骤2根据式(21)计算越界数列hβ, 同时得到越界的机会约束集合Cy, k={Cj|hβ, j > 0}。如果Cy, k=Ø, 计算结束; 否则, k=1时, 采用式(22)更新调节因子; k > 1时, 如果Cy, k⊆Cy, k-1, 采用式(16)更新调节因子, 否则, ak=ρ·ak-1。
步骤3如果max(hβ) < ζ (ζ为一较小的数值), 则计算结束; 否则, 如果k < kmax, 转到步骤1, 如果k=kmax, 计算结束, 并输出最终结果。如果达到最大迭代次数kmax仍未找到最优解, 说明满足给定概率约束的解不存在, 此时需要决定是否进一步减小β值。
3 算例分析
3.1 4节点算例
3.1.1 算例数据
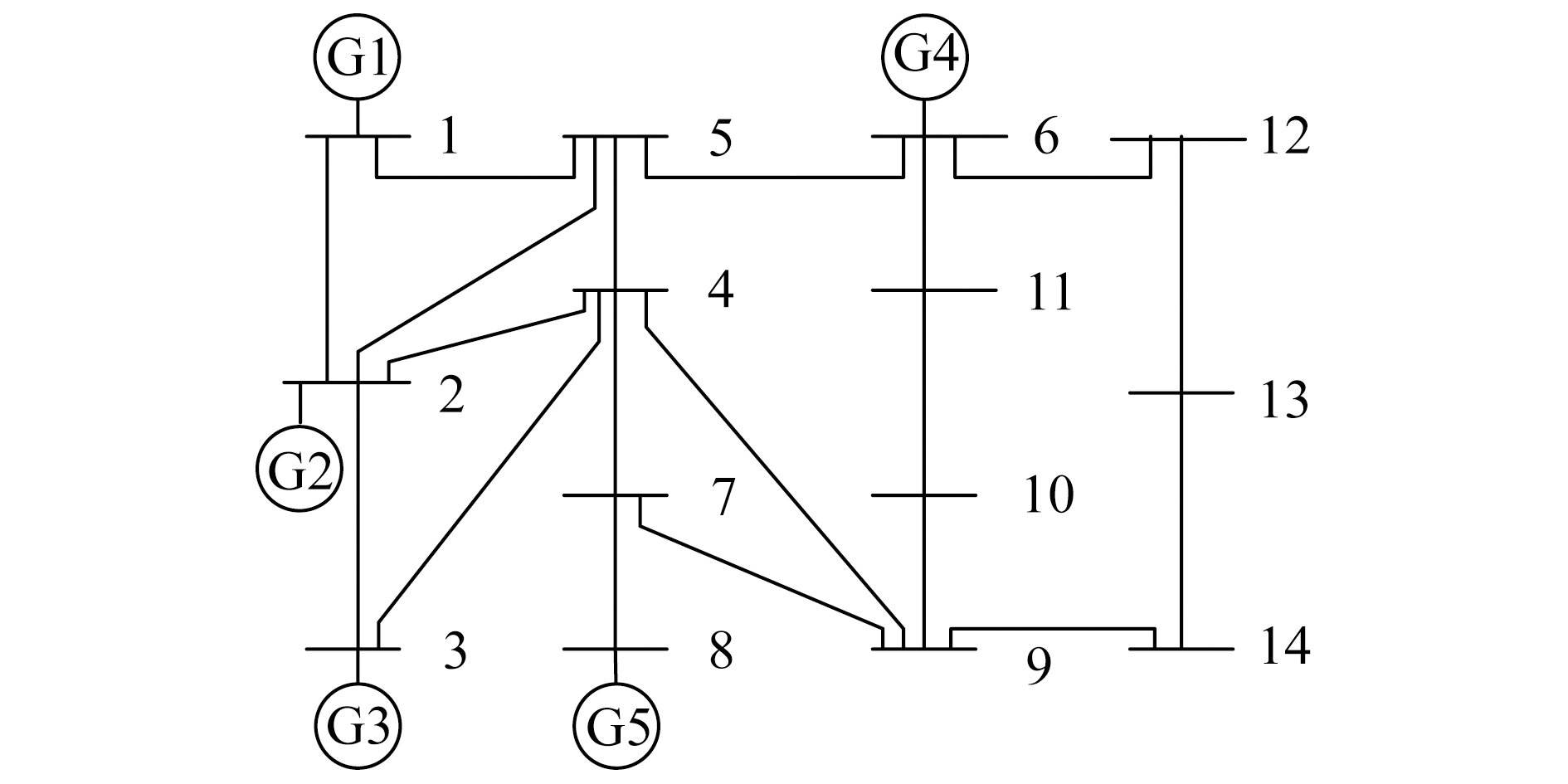
算例系统如图 1所示。系统节点参数、负荷参数、发电机维修率及负荷半不变量数据均见文献[15-16]。
本算例选择节点9和12为风力发电场的并网点, 当前风电场预测值分别为22 MW和20 MW。表 1列出了以5 MW为统计区间的风电功率预测误差前四阶半不变量, 只包括与本文算例相关的部分数据。功率基准值为100 MW。机会约束包括线路视在功率和节点电压幅值约束, 设定置信水平均为95%。为说明线路传输功率越限, 设置节点2和节点3之间的支路视在功率上限为50 MW; 其他支路潮流的视在功率上限为200 MW。
表 1
风电预测误差的半不变量统计(部分)
| $P_{\mathrm{W}}^{\mathrm{d}}$ | 1 | 2 | 3 | 4 |
| [20, 25) | 0.1092 | 0.0198 | 0.0027 | 0.0004 |
| [40, 45) | 0.0781 | 0.0212 | 0.0019 | -0.0001 |
| [50, 55) | 0.0442 | 0.0241 | 0.0034 | 0.0005 |
3.1.2 中间计算过程分析
采用本文所提的方法, 终止条件为max(hβ) < 5×10-5, 经过12次迭代后可得到符合终止调节的解, 迭代过程及计算量见表 2。其中, Nk为第k次迭代的越界约束的个数, Ik为第k次迭代时内点法的迭代次数, Mk为第k次迭代的越界约束。
表 2
迭代过程及计算量
| $k$ | $N_{k}$ | $I_{k}$ | $M_{k}$ | $k$ | $N_{k}$ | $I_{k}$ | $M_{k}$ |
| 1 | 7 | 12 | $C_{1}-C_{7}$ | 7 | 2 | 12 | $C_{1}, C_{7}$ |
| 2 | 4 | 14 | $C_{1}, C_{2}, C_{4}, C_{7}$ | 8 | 1 | 12 | $C_{7}$ |
| 3 | 2 | 14 | $C_{1}, C_{7}$ | 9 | 1 | 14 | $C_{7}$ |
| 4 | 2 | 18 | $C_{1}, C_{7}$ | 10 | 1 | 18 | $C_{7}$ |
| 5 | 2 | 13 | $C_{1}, C_{7}$ | 11 | 1 | 18 | $C_{7}$ |
| 6 | 2 | 14 | $C_{1}, C_{7}$ | 12 | 0 | 13 |
表 2中I1为第一步优化模型的迭代次数。Cy, 1中含有如下7个元素
| $ \left\{\begin{array}{l} C_{1}=S_{23}^{2}-\left(S_{23}^{\max }\right)^{2} \\ C_{2}=S_{32}^{2}-\left(S_{32}^{\max }\right)^{2} \\ C_{3}=U_{7}-U_{7, \max } \\ C_{4}=U_{9}-U_{9, \max } \\ C_{5}=U_{10}-U_{10, \max } \\ C_{6}=U_{11}-U_{11, \max } \\ C_{7}=U_{12}-U_{12, \max } \end{array}\right. $ |
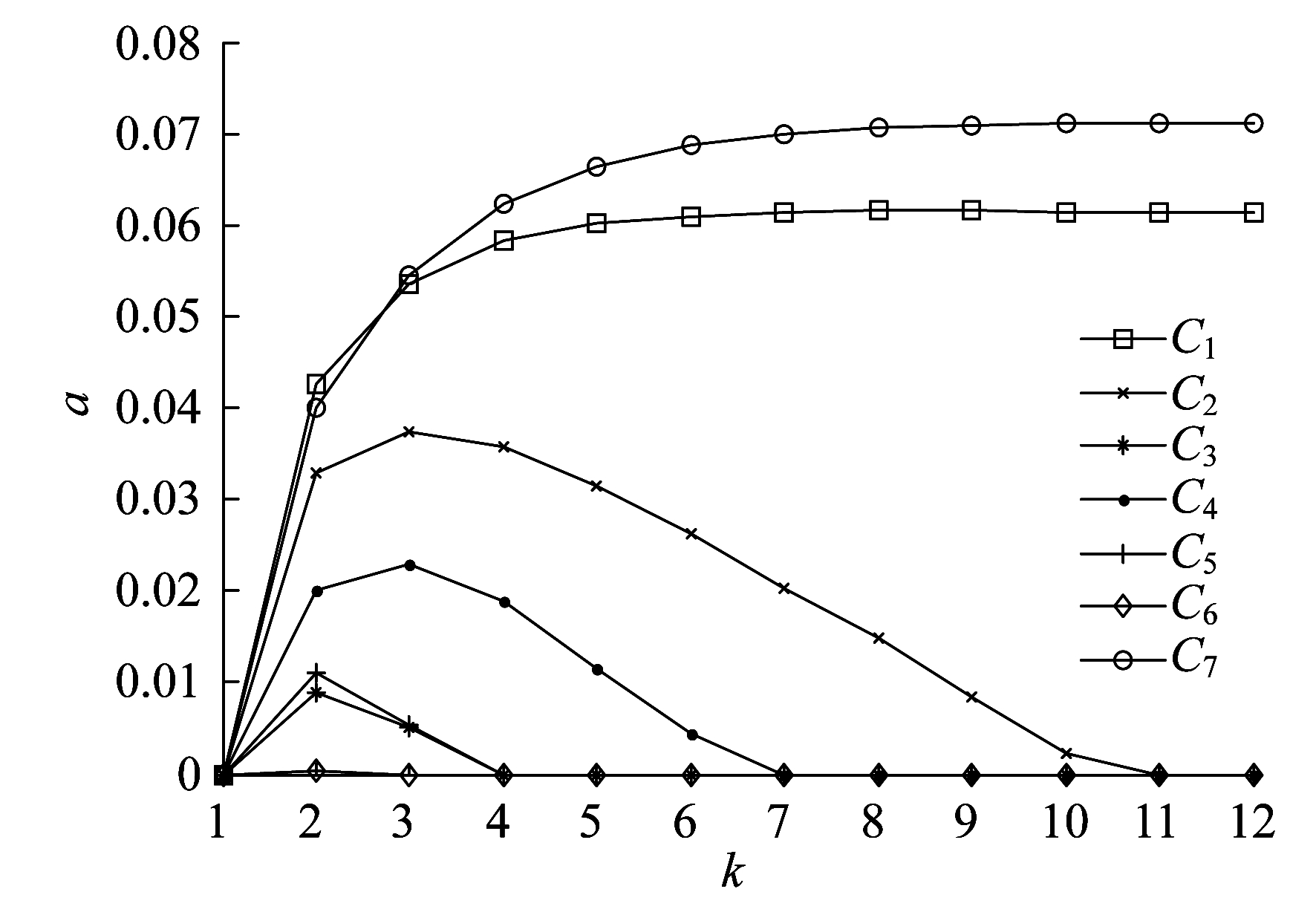
即当调节因子a=0时, 支路2-3之间存在传输功率越限, 节点7和节点9~12的电压大于其上限值。随着迭代过程中不断更新调节因子, 越界约束的个数逐渐减小至零。a中非零元素对应于迭代中的越限机会约束, 其中第1次迭代中有7个机会约束越限, 迭代结果如图 2所示。
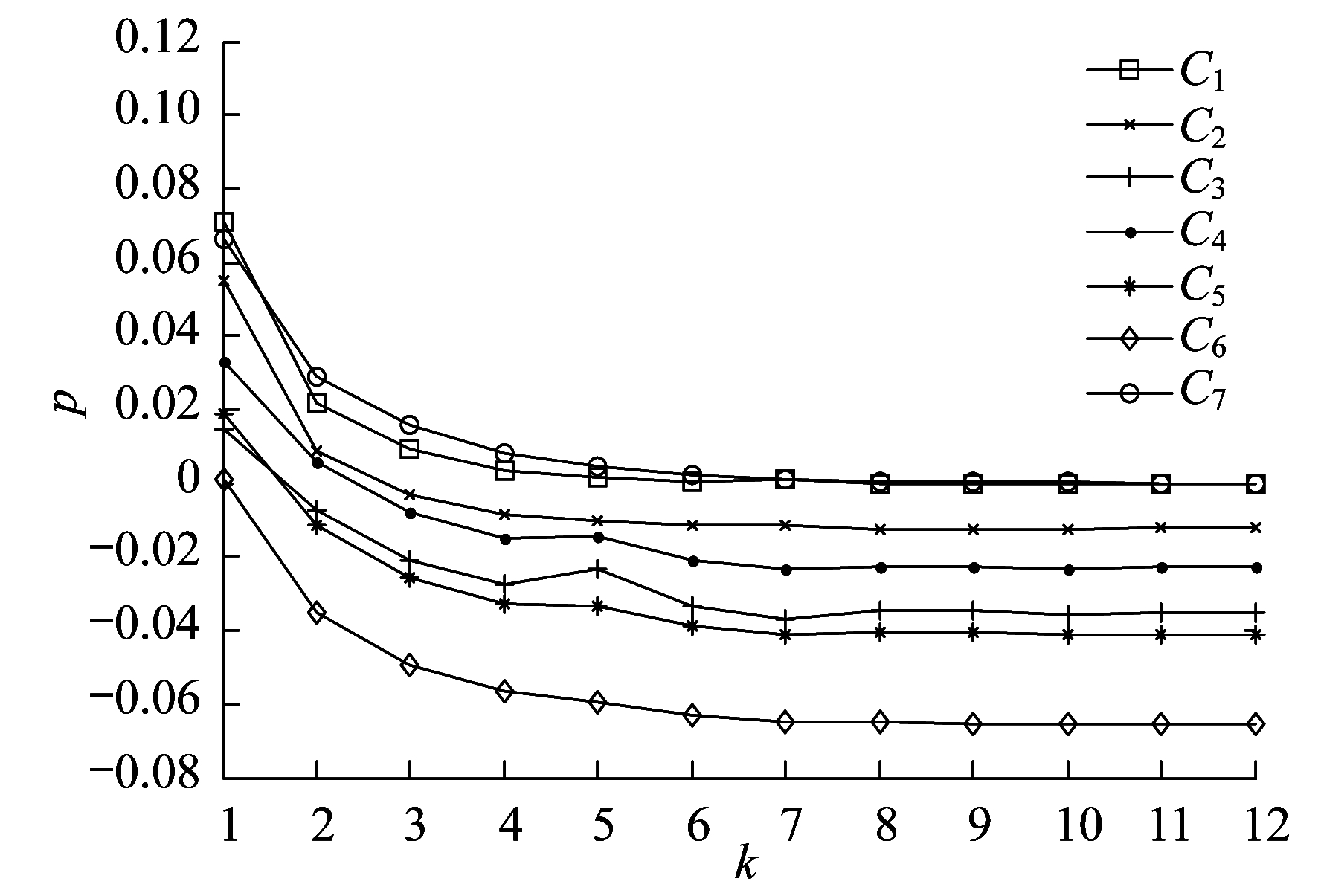
当某一机会约束满足后, 其对应的调节因子的元素变为零, 越界约束的个数减少, 当迭代结束时为零。图 3给出了迭代过程中7个机会约束对应的分位点的变化。从图 3的结果还可以得到:若终止条件采用max(hβ) < 1×10-4, 则经过8次迭代可得到满意解。
根据表 2, 图 2和图 3可以得出如下结论。整个计算过程中牛顿步迭代次数为172, 是12次迭代中第1步优化模型的迭代次数之和; 本算例中, C1和C7的变化对系统的总迭代次数影响较大, 因此当迭代结束时, C1和C7小于零的概率接近给定的置信度。虽然最终解a中对应于C2~C6的元素为零, 然而a中对应于C1和C7的元素的分量却增大, 最终C2~C6满足机会约束。从表 2可以看出, 计算过程中Cy, k⊆Cy, k-1, 即越限的机会约束数目保持不增, 具有良好的收敛性。
3.1.3 最终结果分析
将本文所采用的随机最优潮流(SOPF)与确定性最优潮流方法(Deterministic Optimal Power Flow, DOPF)进行计算和比较:两种方法下的发电机出力调度方案、节点电压、支路3线路功率, 以及C1~C7小于零的概率值分别如表 3~6所示。
表 3
发电机出力比较
| 发电机 | 有功功率(p.u.) | 无功功率(p.u.) | |||
| DOPF | SOPF | DOPF | SOPF | ||
| 1 | 1.427 | 1.326 | 0.032 | 0.083 | |
| 2 | 0.262 | 0.242 | 0.190 | 0.160 | |
| 3 | 0.222 | 0.340 | 0.201 | 0.187 | |
| 4 | 0 | 0 | 0.007 | -0.060 | |
| 5 | 0 | 0 | 0.051 | 0.159 | |
表 4
节点电压比较
| 节点 | 电压幅值(p.u.) | 电压相角(rad) | |||
| DOPF | SOPF | DOPF | SOPF | ||
| 1 | 1.060 | 1.004 | 0 | 0 | |
| 2 | 1.042 | 0.985 | -0.053 | -0.054 | |
| 3 | 1.015 | 0.960 | -0.144 | -0.143 | |
| 4 | 1.023 | 0.966 | -0.103 | -0.108 | |
| 5 | 1.024 | 0.966 | -0.085 | -0.088 | |
| 6 | 1.052 | 0.979 | -0.115 | -0.120 | |
| 7 | 1.051 | 1.000 | -0.105 | -0.111 | |
| 8 | 1.060 | 1.027 | -0.105 | -0.111 | |
| 9 | 1.048 | 0.990 | -0.105 | -0.112 | |
| 10 | 1.041 | 0.979 | -0.113 | -0.121 | |
| 11 | 1.041 | 0.974 | -0.120 | -0.127 | |
| 12 | 1.060 | 0.989 | -0.094 | -0.096 | |
| 13 | 1.037 | 0.966 | -0.117 | -0.123 | |
| 14 | 1.025 | 0.960 | -0.128 | -0.137 | |
表 5
支路3线路功率比较
| 首端为节点$2(\mathrm{p}. \mathrm{u}.)$ | 首端为节点$3(\mathrm{p}. \mathrm{u}.)$ | ||
| DOPF | SOPF | DOPF | SOPF |
| $49.92+\mathrm{j} 2.61$ | $43.36+\mathrm{j} 2.52$ | $-48.84-\mathrm{j} 2.66$ | $-42.44-\mathrm{j} 2.79$ |
表 6
C1~C7小于零的概率值
| 方法 | $C_{1}$ | $C_{2}$ | $C_{3}$ | $C_{4}$ | $C_{5}$ | $C_{6}$ | $C_{7}$ |
| DOPF | 0.681 | 0.746 | 0.605 | 0.497 | 0.736 | 0.941 | 0.118 |
| SOPF | 0.950 | 0.971 | 1.000 | 0.994 | 1.000 | 1.000 | 0.950 |
由表 4可以看出, 采用本文SOPF方法得到的节点7和节点9~12的电压幅值比DOPF方法的计算值小, 可有效地预防风电场功率波动造成的节点电压越限。根据表 5数据, 采用DOPF计算可得到的调度方案中支路2-3的视在功率为49.988 MW, 在实时调整中有可能出现线路阻塞的情况。采用SOPF方法, 支路2-3的视在功率为43.433 MW, 离设定的线路功率极限(50 MW)保持一定的裕度。表 6表明, 采用SOPF方法得到的解可有效地满足机会约束, 即C1 < 0的概率大于等于0.95, 并且C1~C7刚达到所设定的置信度, 说明调节过程保证了调整量最小。
3.2 118节点算例
将风力发电机组接入节点9和节点26, 预测功率分别为50 MW和40 MW, 预测误差的概率参数如表 1所示, 并假设负荷的方差为其预测值的8%, 约束支路8上的潮流上限设为400 MW。第1次迭代得到5个越限的机会约束数为
| $ \left\{\begin{array}{l} \mathrm{C}_{118,1}=S_{85}^{2}-\left(S_{85}^{\max }\right)^{2} \\ \mathrm{C}_{118,2}=S_{58}^{2}-\left(S_{58}^{\max }\right)^{2} \\ \mathrm{C}_{118,3}=U_{9}-U_{9, \max } \\ \mathrm{C}_{118,4}=U_{43}-U_{43, \max } \\ \mathrm{C}_{118,5}=U_{98}-U_{98, \max } \end{array}\right. $ |
即支路5~8之间存在传输功率越限, 节点3~5的电压大于其上限值。采用SOPF方法计算迭代10次后满足终止条件max(hβ) < 5.0×10-5, 调节过程如表 7所示。
表 7
118节点系统迭代过程及计算量
| $k$ | $N_{\mathrm{k}}$ | $I_{1}$ | $M_{\mathrm{k}}$ | $k$ | $N_{\mathrm{k}}$ | $I_{1}$ | $M_{\mathrm{k}}$ |
| 1 | 5 | 21 | $C_{1} \sim C_{5}$ | 6 | 2 | 22 | $C_{4}, C_{5}$ |
| 2 | 4 | 22 | $C_{1}, C_{2}, C_{4}, C_{5}$ | 7 | 2 | 21 | $C_{4}, C_{5}$ |
| 3 | 4 | 22 | $C_{1}, C_{2}, C_{4}, C_{5}$ | 8 | 1 | 22 | $C_{4}$ |
| 4 | 4 | 22 | $C_{1}, C_{2}, C_{4}, C_{5}$ | 9 | 1 | 22 | $C_{4}$ |
| 5 | 2 | 22 | $C_{4}, C_{5}$ | 10 | 0 | 21 |
表 8是两种方法下初次越界的机会约束最终的概率值。最优潮流和随机潮流的目标函数值分别为126 236.15元和126 360.57元。由表 8可以看出, 118节点算例显示SOPF方法仍具有良好的收敛速度。
表 8
C118, 1~C118, 5小于零的概率值
| 方法 | $C_{118, 1} < 0$ | $C_{118, 2} < 0$ | $C_{118, 3} < 0$ | $C_{118, 4} < 0$ |
| DOPF | 0.930 | 0.930 | 0.696 | 0.576 |
| SOPF | 0.950 | 0.950 | 0.950 | 0.950 |
本文所有程序均采用Intel(R) Core(TM) i5-2410M CPU@ 2.3 GHz计算机, 在MATLAB 2010a环境下运行, 相关算法基于Matpower4.0中的子程序, 计算时间如表 9所示。
表 9
算例计算时间
| 系统 | 时间/s | |
| DOPF | SOPF | |
| 14节点 | 0.226 | 9.128 |
| 118节点 | 0.569 | 23. 159 |
综上可见, 与DOPF相比, 通过SOPF方法得到的调度方案与电压和线路功率极限值保持了一定的距离, 是更为安全的运行点, 能经受和适应风电功率预测误差和负荷功率波动的影响。
4 结语
随机最优潮流计算是考虑随机变量的电力系统分析的基础。本文基于机会约束规划建立含风电场的电力系统随机最优潮流模型, 并采用内点法结合随机调节因子更新来求解该模型。利用分位点和机会约束概率之间的等价关系, 在内点法中加入与分位点相关的调节因子, 通过更新调节因子来调节机会约束满足的概率。该方法结合了内点法和半不变量理论的优点。算例分析表明, 该方法可以有效求解含波动性电源和负荷的电力系统随机最优潮流。
参考文献
-
[1]KANG J J, YUAN J H, HU Z G. Review on wind power development and relevant policies in China during the 11th Five-Year-Plan period[J]. Renewable and Sustainable Energy Reviews, 2012, 16(4): 1907-1915. DOI:10.1016/j.rser.2012.01.031
-
[2]SCHELL E A. Probabilistic and stochastic optimal powerflow[D]. Alberta, Canada: University of Calgary, 2006.
-
[3]计及风电相关性的二阶锥动态随机最优潮流[J]. 电力系统自动化, 2018, 42(5): 41-47. DOI:10.7500/AEPS20170605003
-
[4]WANG S, YANG H M, ZUO S. Optimal dispatch of power system with stochastic wind generation[J]. Advances in Engineering Design and Optimization, 2011, 37/38: 783-786.
-
[5]考虑风速相关性和可调度负荷不确定性的区间最优潮流[J]. 中国电机工程学报, 2016, 36(10): 2628-2637.
-
[6]ZHANG H, LI P. Chance constrained programming for optimal power flow under uncertainty[J]. IEEE Trans on Power Systems, 2011, 26(4): 2417-2424. DOI:10.1109/TPWRS.2011.2154367
-
[7]计及风电和需求响应的电网动态经济调度[J]. 上海电力学院学报, 2016, 32(3): 296-300.
-
[8]基于机会约束规划的最优旋转备用容量确定[J]. 电网技术, 2006, 30(20): 14-19. DOI:10.3321/j.issn:1000-3673.2006.20.004
-
[9]基于风速预测和随机规划的含风电场电力系统动态经济调度[J]. 中国电机工程学报, 2009, 29(4): 41-47. DOI:10.3321/j.issn:0258-8013.2009.04.007
-
[10]WANG Q F, GUAN Y P, WANG J H. A chance-constrained two-stage stochastic program for unit commitment with uncertain wind power output[J]. IEEE Trans on Power Systems, 2012, 27(1): 206-215. DOI:10.1109/TPWRS.2011.2159522
-
[11]LIU Z P, WEN F S, LEDWICH G. Optimal siting and sizing of distributed generators in distribution systems considering uncertainties[J]. IEEE Trans Power Delivery, 2011, 26(4): 2541-2551. DOI:10.1109/TPWRD.2011.2165972
-
[12]WANG H, MURILLO-SANCHEZ C E, ZIMMERMAN R D, et al. On computational issues of market-based optimal power flow, power systems[J]. IEEE Transactions on Power Systems, 2007, 22(3): 1185-1193. DOI:10.1109/TPWRS.2007.901301
-
[13]FINNEY D J. The advanced theory of statistics[J]. Annals of Human Genetics, 2012, 12(1): 211-212.
-
[14]微电网多目标动态优化调度模型与方法[J]. 电力自动化设备, 2013, 33(3): 100-107. DOI:10.3969/j.issn.1006-6047.2013.03.017
-
[15]王锡凡.电力系统优化规划[M].北京: 水利电力出版社, 1990: 313-322.
-
[16]ZIMMERMANR D, MURILLO-SANCHEZ C E, THOMAS R J, et al. Steady-state operations, planning and analysis tools for power systems research and education[J]. IEEE Transactions on Power Systems, 2011, 26(1): 12-19. DOI:10.1109/TPWRS.2010.2051168