|
|
|
发布时间: 2019-12-10 |
|
|
|
|
收稿日期: 2018-04-13
基金项目: 上海市科学技术委员会项目(18DZ1202105, 18DZ1202302)
中图法分类号: TK83
文献标识码: A
文章编号: 1006-4729(2019)06-0511-07
|
摘要
选用NREL 5 MW风力机, 采用FLUENT软件对塔筒式和桁架式两种塔架的风力机整机进行了非定常数值模拟。结果表明:桁架受到的升力和阻力都远小于塔筒, 桁架式的结构更有利于自身安全; 气流在通过桁架后的速度梯度和湍流强度都大于塔筒式风力机, 而不同截面的速度都略小于塔筒式风力机。因此, 桁架式风力机的布置间距要考虑略大于塔筒式风力机的布置间距。
关键词
风力机; 塔影效应; 塔筒式; 桁架式; 尾迹; 数值模拟
Abstract
The NREL 5 MW wind turbine is chosen and unsteady numerical simulation of tower shadow effect of monopile and truss type tower wind turbine are carried out by using FLUENT software.The results show that the lift and drag of the truss type tower are far less than the monopile type tower, so truss structure is more conducive to their own safety.The velocity gradient and the turbulence intensity of airflow is greater than the monopile type tower wind turbine when it passes truss type tower wind turbine, but the velocity of different sections is slightly smaller than the tower type wind turbine.So the layout spacing of the truss type tower wind turbine should be slightly larger than the monopile type tower wind turbine layout spacing.
Key words
wind turbine; tower shadow effect; monopole type tower; truss type tower; wake; numerical simulation
塔架支撑整个风力机, 同时还要承受来流风的压力和风力机运行的载荷。塔架的存在势必会对风力机尾迹产生一定的影响, 即为塔影效应。所谓塔影效应是指当自由来流风经过塔架时, 由于塔架的阻挡导致风速减小以及作用在风轮上的载荷产生周期性震荡的现象。塔影效应会造成风力机输出功率减小以及气动载荷的波动, 进而影响风力机叶片及塔架的疲劳寿命, 并且其对尾迹流场的扰动也会往风力机下游传递, 对风电场中的下游风力机产生影响。因此, 研究塔影效应对风力机尾迹的影响非常重要。
国内外对于塔影效应都有一定的研究, 研究对象主要集中于塔筒式风力机。CHATTOT J J[1]建立了螺旋涡模型(该模型相当于一个下风向装置), 分别对其在5 m/s、7 m/s、10 m/s、12 m/s的风速及30°的偏航角度下进行了分析, 结果表明, 这一模型能够在一定程度上应用于塔影效应的研究, 成本低, 通用性强。LACKNER M A等人[2]建立了二维和三维模型来模拟上风向风力机的塔影效应, 并对二维和三维模型的速度场进行了对比, 对三维模型的不足之处进行了改进。REISO M等人[3]建立了下风向风力机塔架的二维模型, 并采用一种新方法进行了定常和非定常模拟, 分析了塔影效应下的风力机尾迹宽度、湍流强度变化及速度损失。范忠瑶等人[4]使用FINETM/Turbo软件对上风向风力机叶片和塔架进行了数值计算, 然后对叶片载荷、表面压力、法向力系数及流场分布进行了分析, 结果表明, 塔架的影响会使风力机的载荷发生很大变化, 同时风轮的旋转也会使塔架的受力不均。封晨颖[5]以风力机设计理论为基础, 设计了10 kW风力机, 并进行了载荷计算; 建立了塔架和翼型截面的二维模型, 分析了相对距离对翼型周围流场分布和压力系数的影响; 建立了风力机整机的三维模型, 分析了塔架对叶片的压力分布和推力的影响。孔屹刚等人[6]在考虑了风剪切和塔影效应的基础上, 建立了风力机的风速模型, 分析了不同塔架高度、塔架直径、风剪切系数等对风力机风速的影响。范忠瑶[7]对塔架的脱落涡与风力机叶片的相互作用等气动问题进行了数值模拟研究。
本文选用NREL 5 MW[8]风力机, 采用SSTk-ω湍流模型和滑移网格技术对其进行模拟, 对比分析了塔筒式和桁架式风力机的塔影效应对风力机尾迹流场的影响。
1 物理模型及数值计算方法
1.1 物理模型
1.2 几何模型及网格划分
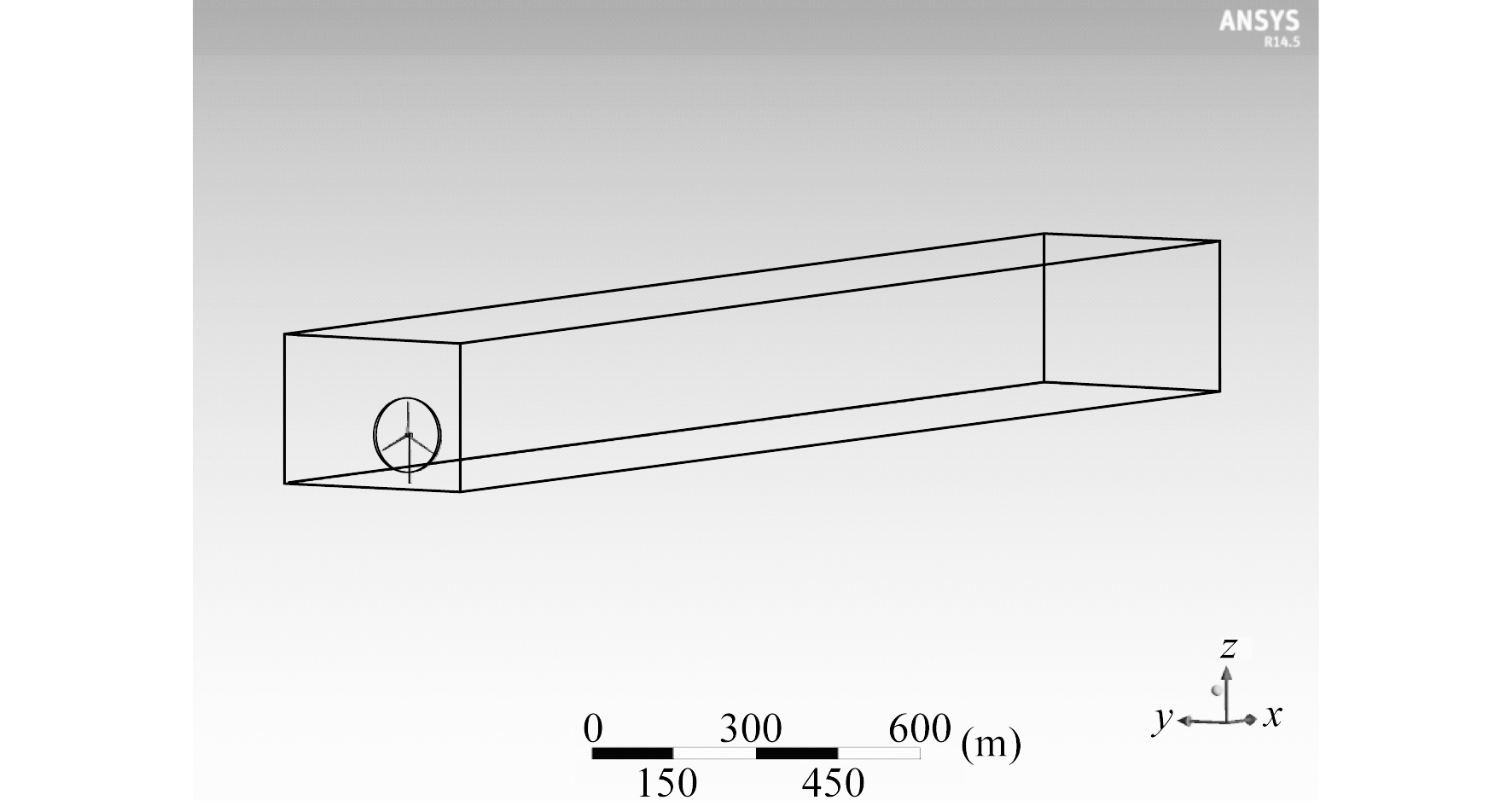
首先建立风力机模型, 然后建立计算流场模型。外围流场采用长方体形流场, 并且外围流场分成两个部分, 一部分为包含风力机模型的旋转域, 另一部分为旋转域外的静止域。流场模型如图 2所示。
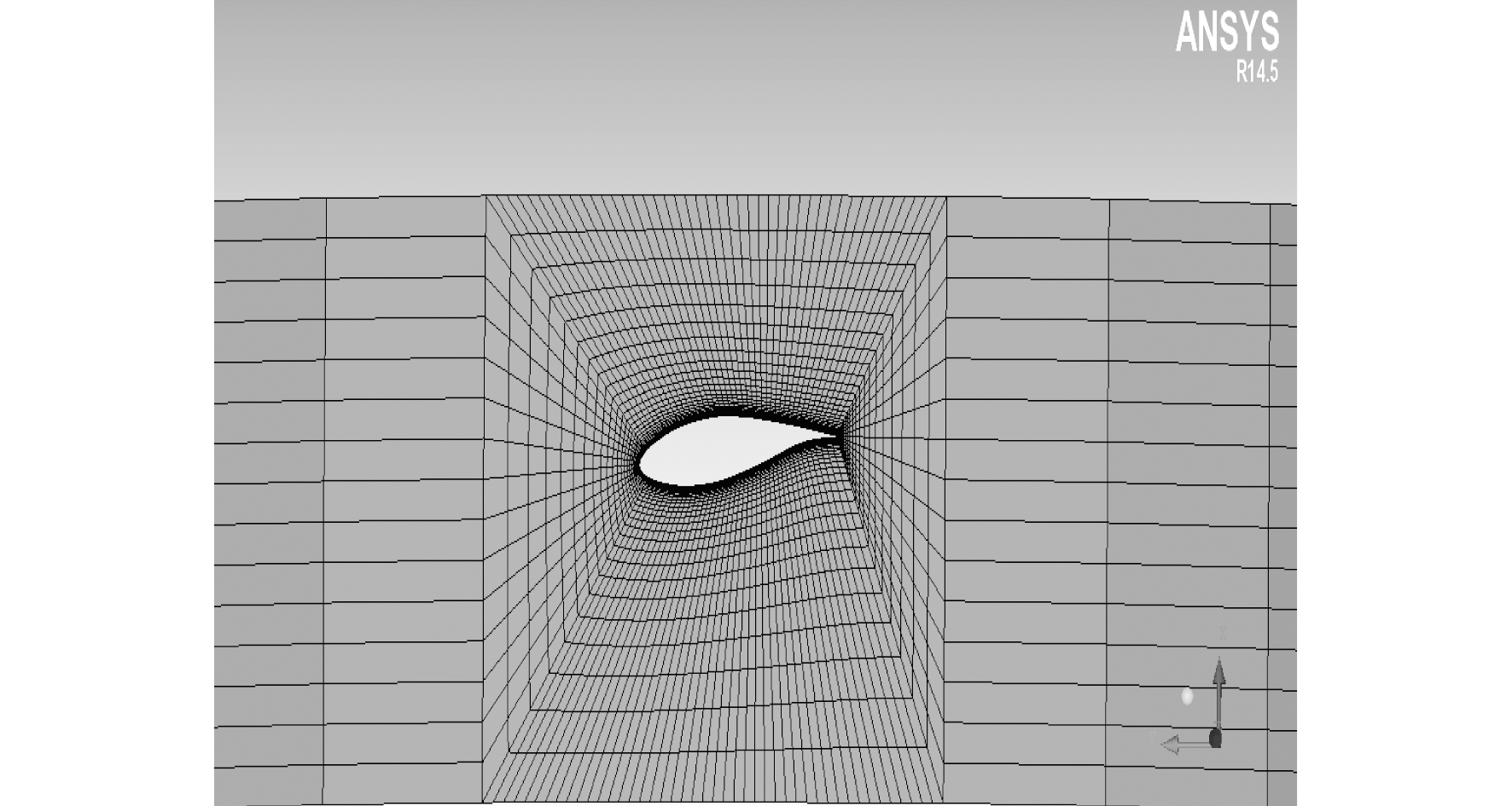
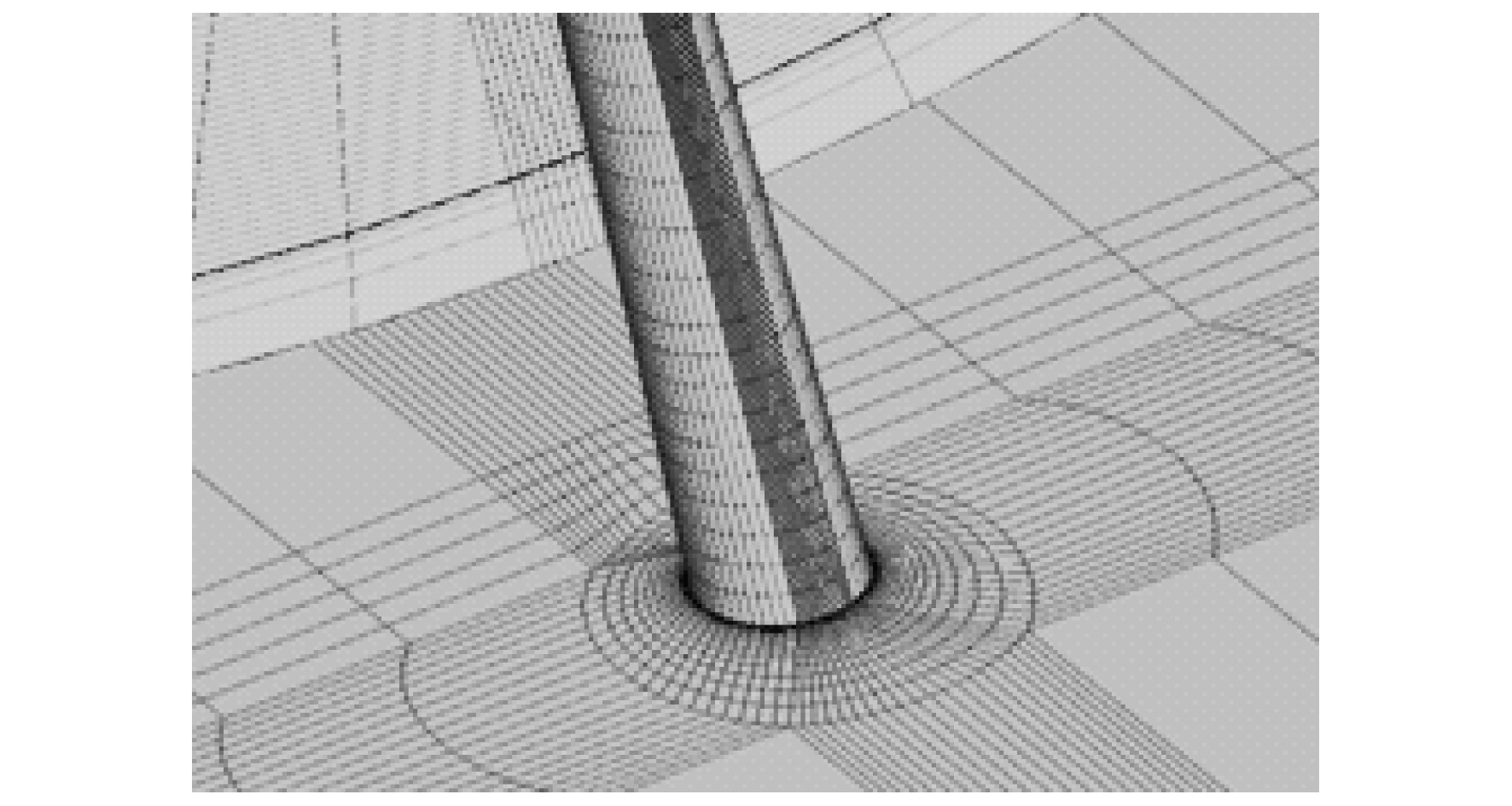
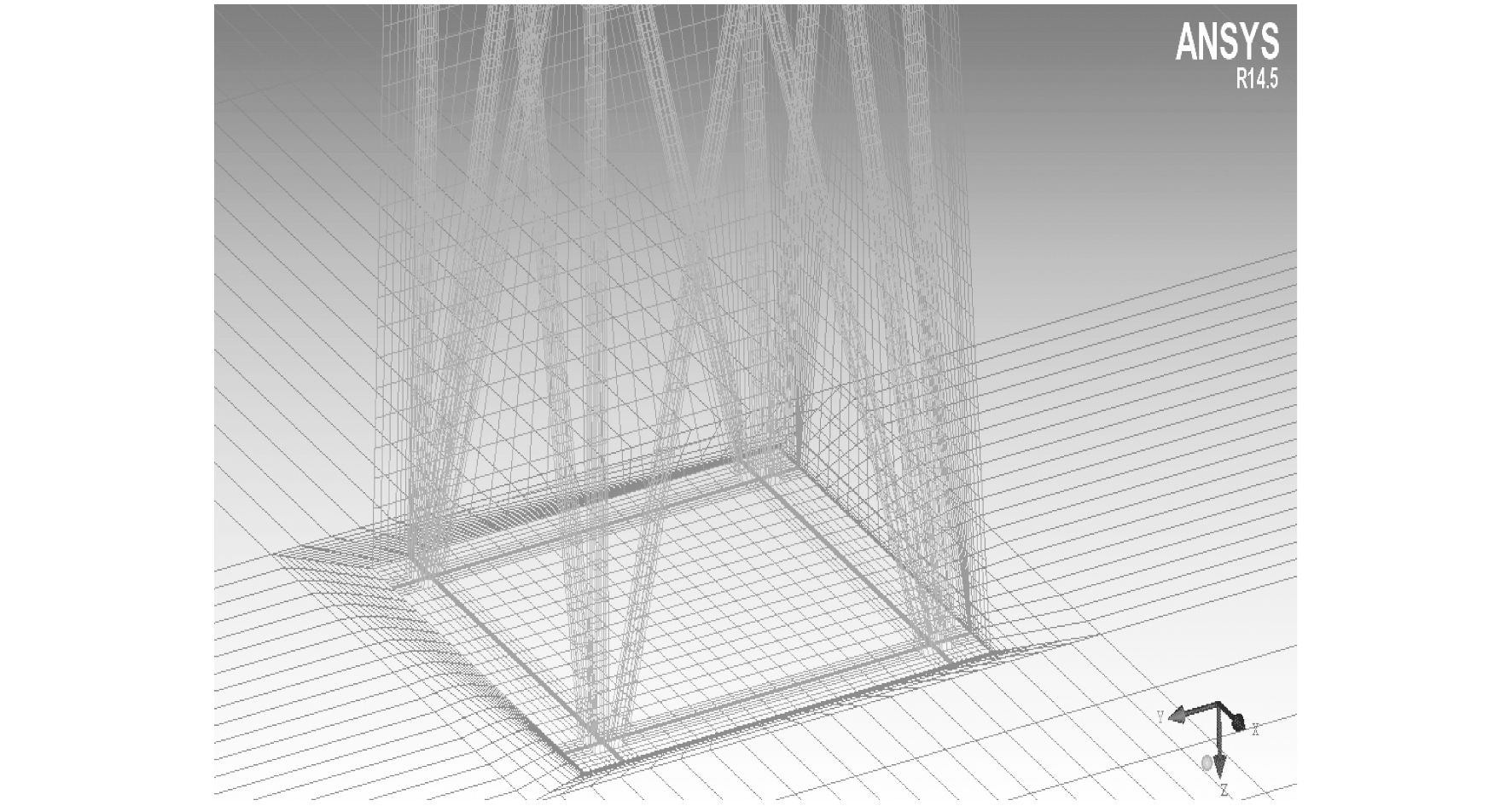
外围流场的入口距离风力机旋转平面1D(126 m), 出口距离风力机旋转平面20D(2 520 m); 旋转域直径为70 m, 其入口距离风力机旋转平面3 m, 出口距离风力机旋转平面3 m。叶片周围、塔架周围网格划分如图 3~图 5所示。
为了满足y+的要求, 叶片第一层网格尺寸为1 mm, 并按1.2的增长率进行网格加密, 加密层数为30层; 塔筒表面第一层网格尺寸为1 mm, 网格增长率为1.15, 加密层数为20层; 桁架表面第一层网格尺寸为1 mm, 网格增长率为1.2, 桁架表面至内区域边界的网格数为15个。塔筒周围网格总数为2.03×106个, 整个计算域网格数为4.0×106个; 桁架所在的小静止域网格数为4.9×105个, 外围大静止域网格数为2.0×106个, 整个计算域网格数为4.5×106个。
1.3 控制方程
本文数值模拟计算基于N-S方程, 考虑到湍流模型需与壁面函数法兼容以及叶轮的旋转效应, 选用带有湍流漩涡修正的RNG k-ε两方程模型, 离散格式为二阶迎风, 利用SIMPLE算法进行求解[9]。采用滑移网格法计算, 设置旋转域, 以叶轮旋转轴为轴进行旋转, 风力机组部件视为刚性, 不考虑流固耦合。
RNG k-ε模型控制方程[10]为:
| $\frac{\partial(\rho k)}{\partial t}+\frac{\partial}{\partial x_{i}}\left(\rho k u_{i}\right)=\frac{\partial}{\partial x_{j}}\left(\alpha_{\mathrm{k}} \mu_{\mathrm{eff}} \frac{\partial k}{\partial x_{j}}\right)+ \\ G_{\mathrm{k}}+G_{\mathrm{b}}-\rho_{\varepsilon}-Y_{\mathrm{M}}+S_{\mathrm{k}}$ | (1) |
| $\frac{\partial(\rho \varepsilon)}{\partial t}+\frac{\partial}{\partial x_{i}}\left(\rho \varepsilon u_{i}\right)=\frac{\partial}{\partial x_{j}}\left(\alpha_{\varepsilon} \mu_{\mathrm{eff}} \frac{\partial \varepsilon}{\partial x_{j}}\right)+ \\ C_{1 \varepsilon} \frac{\varepsilon}{k}\left(G_{\mathrm{k}}+C_{3 \varepsilon} G_{\mathrm{b}}\right)-C_{2 \varepsilon} \rho \frac{\varepsilon^{2}}{k}-R_{\varepsilon}+S_{\varepsilon}$ | (2) |
式中:ρ——空气密度;
k——湍流脉动动能;
t——时间;
xi, xj——空间某一方向(i, j=1, 2, 3);
ui——速度在某一方向上的分量(i=1, 2, 3);
αk——湍流动能普朗特数的倒数;
μeff——有效黏性系数;
Gk——产生的湍流动能;
Gb——由浮力产生的湍流动能;
ρε——耗散项的密度;
YM——在可压缩湍流中过渡的扩散产生的波动;
ε——脉动耗散率;
αε——湍流耗散率普朗特数的倒数;
C1ε, C2ε, C3ε——模型默认常数;
Rε, Sk, Sε——用户自定义项。
2 计算结果分析
2.1 塔影效应下的风力机受力分析
图 6为风力机塔架表面所受到的升力和阻力随风力机叶片旋转的变化曲线。
从图 6可以看出, 对于塔筒式风力机, 每当叶片旋转到塔筒的前方时, 塔筒表面所受到的升力和阻力的大小和方向都发生急剧的转变。这是因为, 此时塔筒正处于风力机叶片的尾迹中, 塔筒对尾迹气流的剧烈扰动使得塔筒的受力发生突变, 如果长时间处于这种影响中会对塔筒造成严重的损坏。对于桁架式风力机, 其所受到的升力和阻力的最大差值分别为9 500 N和8 000 N, 相比于塔筒所受到的最大升力差值32 000 N和最大阻力差值26 000 N, 桁架所受的升力和阻力要明显小于塔筒所受的升力和阻力, 并且没有太大的波动和规律性, 虽然每次叶片旋转到桁架前方时, 桁架所受到的升力和阻力都有所变化, 但变化不明显。造成这些现象的原因, 是因为气流到达桁架时, 有一部分气流可以从桁架的钢柱之间穿过, 另一部分气流则要受到多根钢柱的阻挡作用, 通过每一根钢柱时都要发生绕流现象, 每根绕流的叠加使得气流的扰动变得复杂; 而气流在到达塔筒时则会受到完全阻挡, 使塔筒受到很大的升力和阻力。这也充分说明桁架式风力机的受力远小于塔筒式风力机, 更有利于结构的安全。
2.2 塔影效应下的风力机速度和湍流强度分析
2.2.1 塔影效应对近尾迹流场的影响
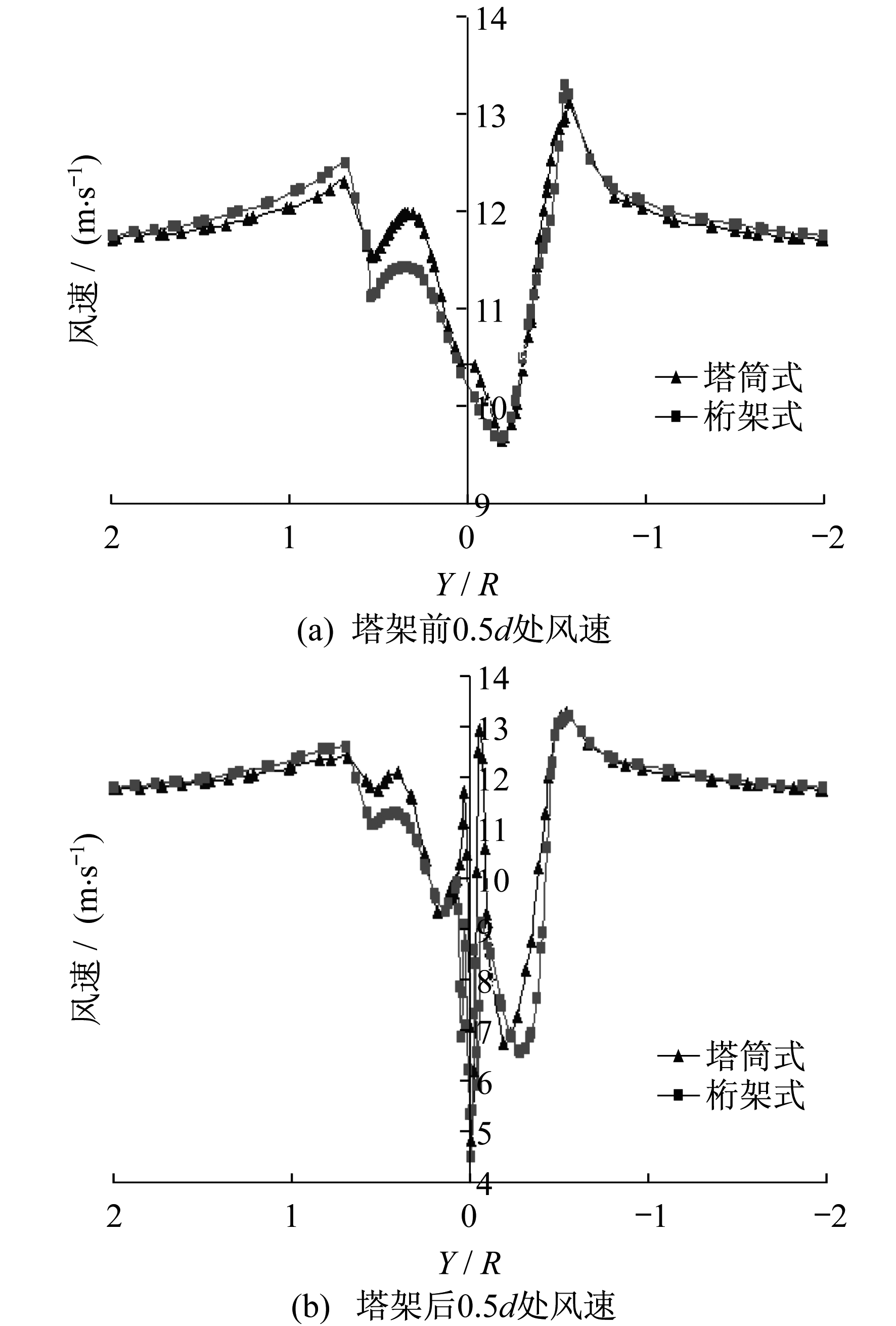
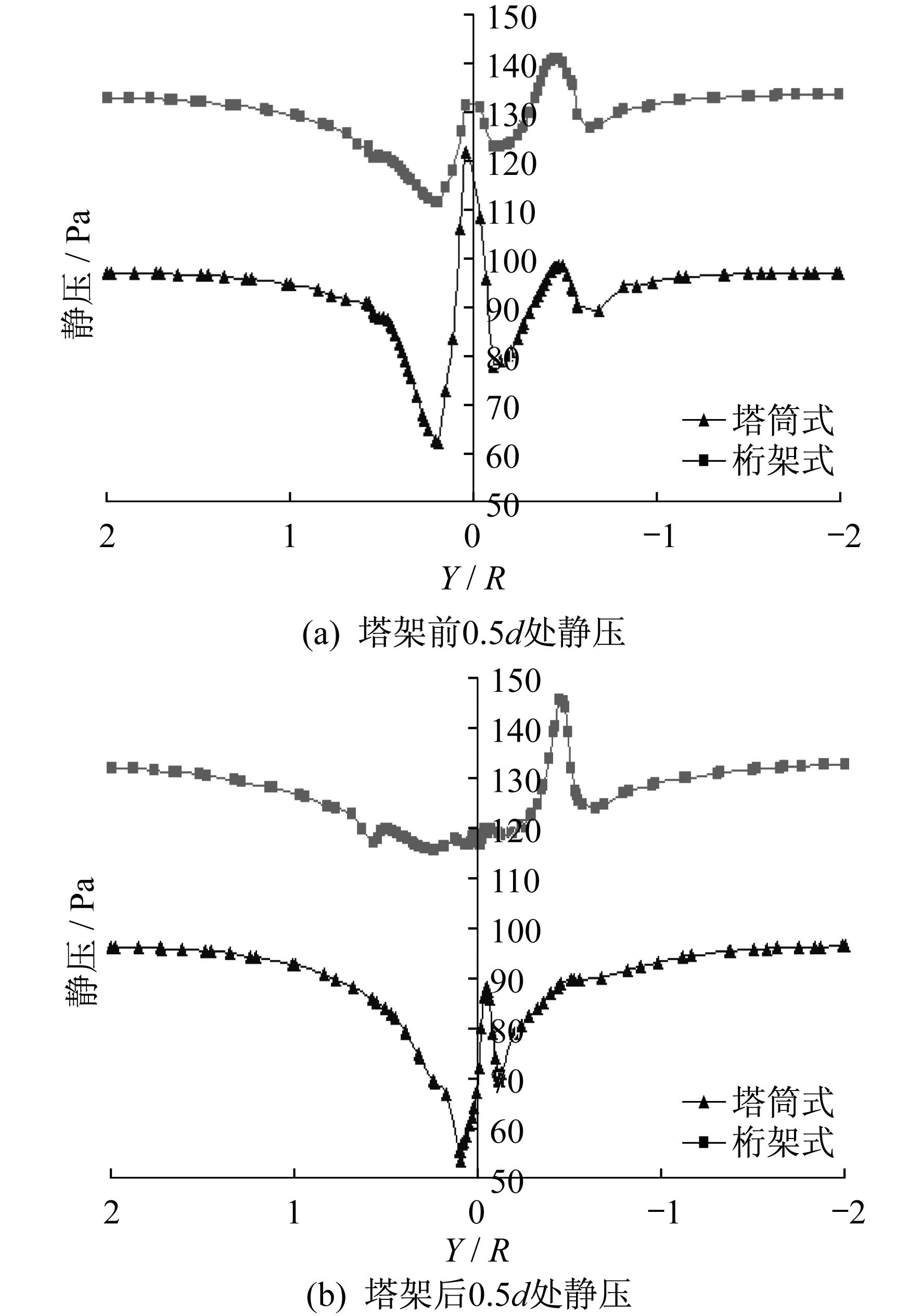
首先分析风力机塔架前后距离塔架比较近的位置处的风速和静压的变化, 提取塔架前0.5d(d为塔架底部直径)和塔架后0.5d处的风速和静压做成曲线, 如图 7和图 8所示。
从图 7可以明显看出, 来流风在两种形式的塔架前后的速度都有明显变化。这种变化在塔架正前方和正后方中心附近的位置最明显, 并且从图 7(b)可以看到, 气流在经过塔架后, 其速度在塔架附近的变化都很剧烈, 但是桁架式风力机的速度变化要小于塔筒式风力机。这是因为气流在经过塔架后很小的距离内, 由于气流在塔架的绕流作用导致塔架正后方的气流速度很小, 而塔架两侧的气流受到挤压, 速度很大, 并且由于气流在塔筒所受到的挤压要大于在桁架的细长钢柱处所受到的挤压, 所以塔筒后方的速度变化要大于桁架。由图 8的静压变化可以看出, 静压在塔架前后也发生了变化, 其中桁架前后的压力变化最大值为30 Pa, 而塔筒前后的压力变化最大值则达到了70 Pa, 桁架前后的压力变化明显小于塔筒, 这也是由塔架结构不同导致的绕流作用不同所引起的。因此, 对于塔架本身来说, 桁架式的结构更安全一些。
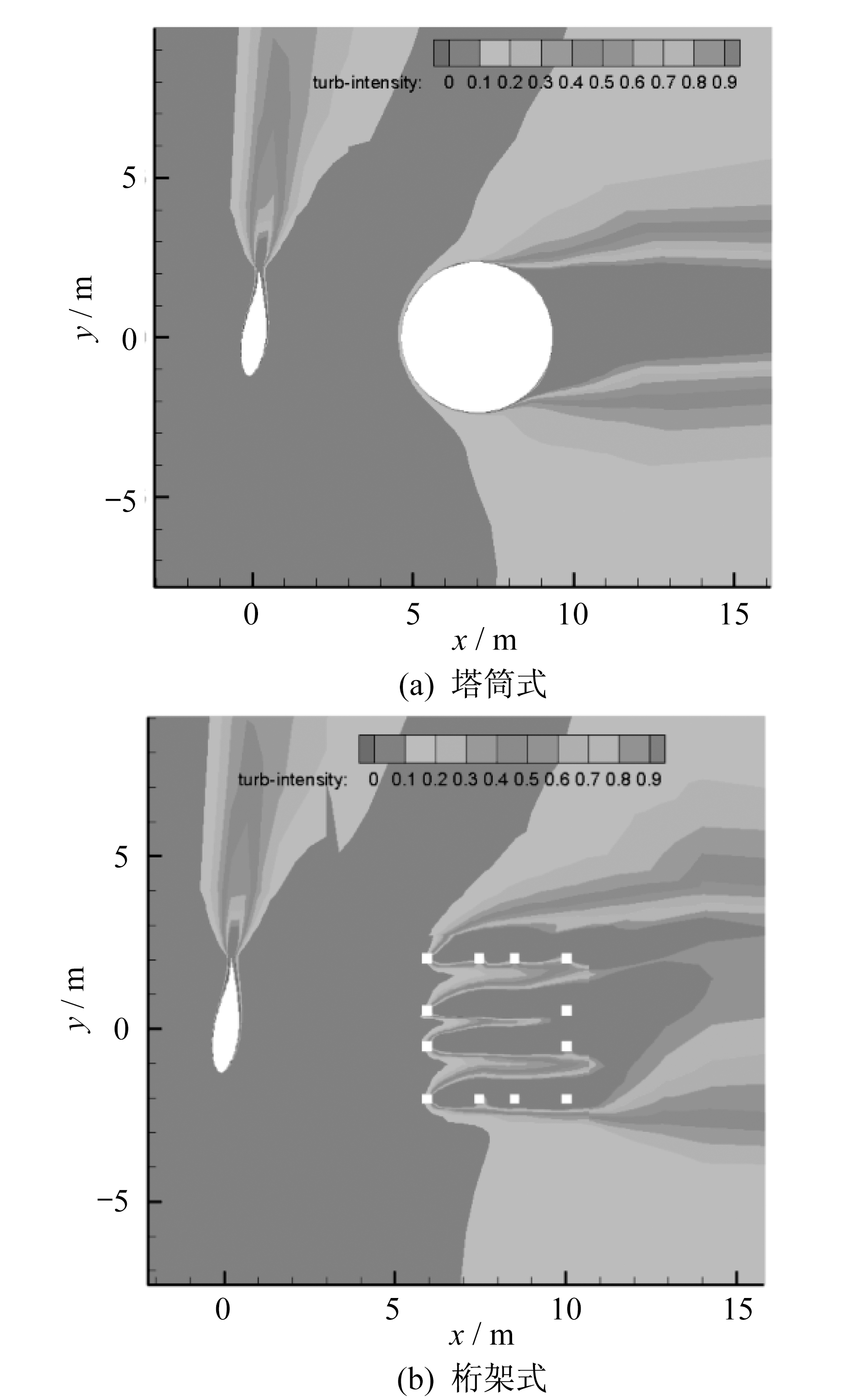
图 9为0.6R处的湍流强度云图。
从图 9可以看出, 塔架的存在会对风力机叶片产生一定的影响。相互影响最严重的地方出现在叶根处, 并且由于塔架的扰动, 使风力机尾迹区产生很大的湍流强度。对比两种形式的塔架可以看出, 桁架式的塔架对风力机尾迹气流的扰动要大于塔筒式的塔架, 其扰动的范围及强度也要大一些。
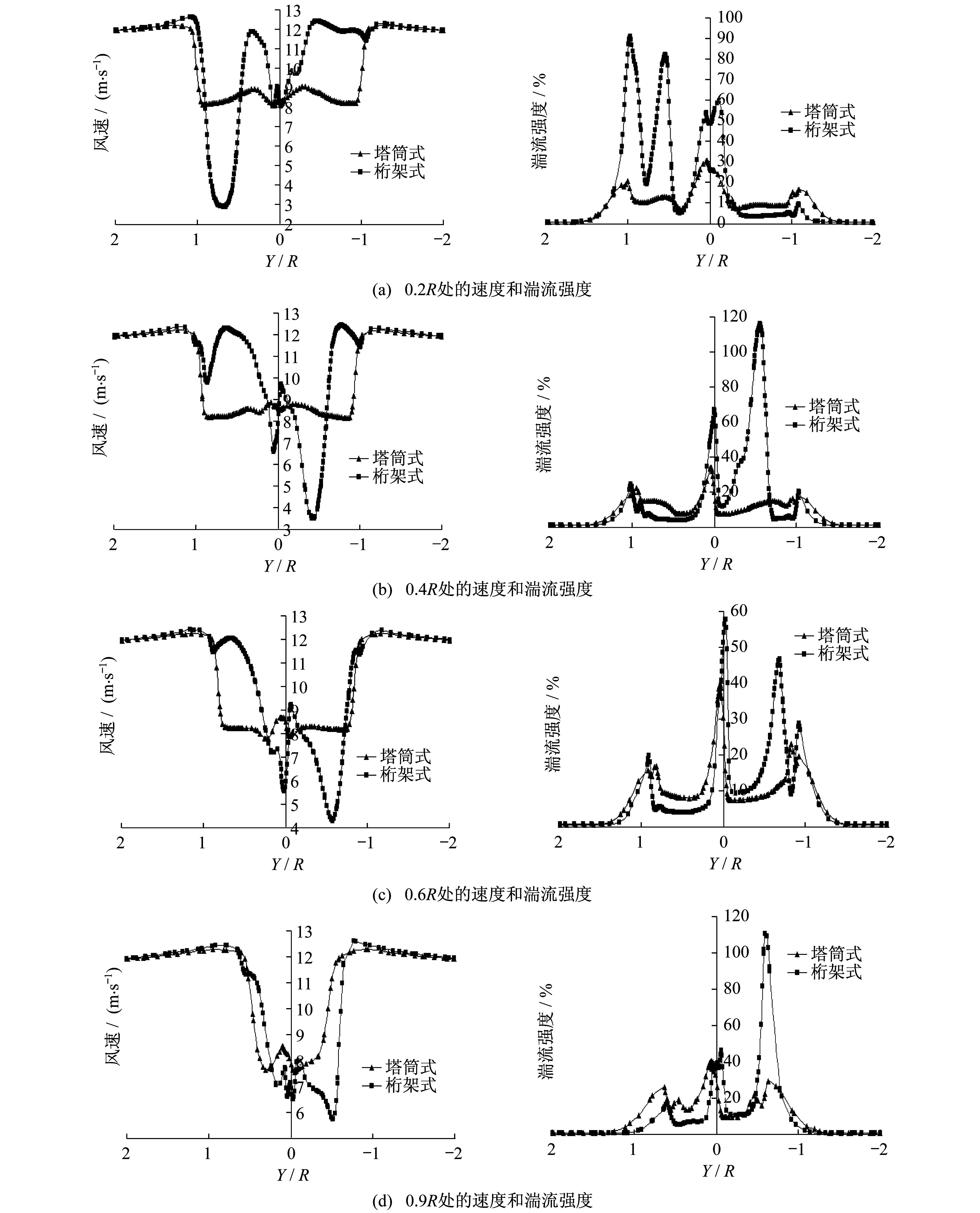
图 10为风力机下游0.5倍风轮直径处, 两种形式塔架不同叶高处的速度和湍流强度对比曲线。从图 10可以看出, 塔筒式风力机的速度最小值和湍流强度最大值都出现在接近塔筒正后方的位置, 速度亏损的最大值约为30%, 湍流强度最大值约为40%;对于桁架式风力机而言, 其速度最小值和湍流强度最大值的出现位置并不固定, 主要是由桁架结构造成的, 在不同叶高处的截面, 其钢柱的位置是不同的, 导致气流绕流钢柱的位置也发生了变化, 桁架式风力机的速度亏损最大值达到了70%, 湍流强度最大值则达到了120%, 明显大于塔筒式风力机。这充分说明桁架对风力机近尾迹的影响要大于塔筒对风力机近尾迹的影响。
2.2.2 塔影效应对远尾迹流场的影响
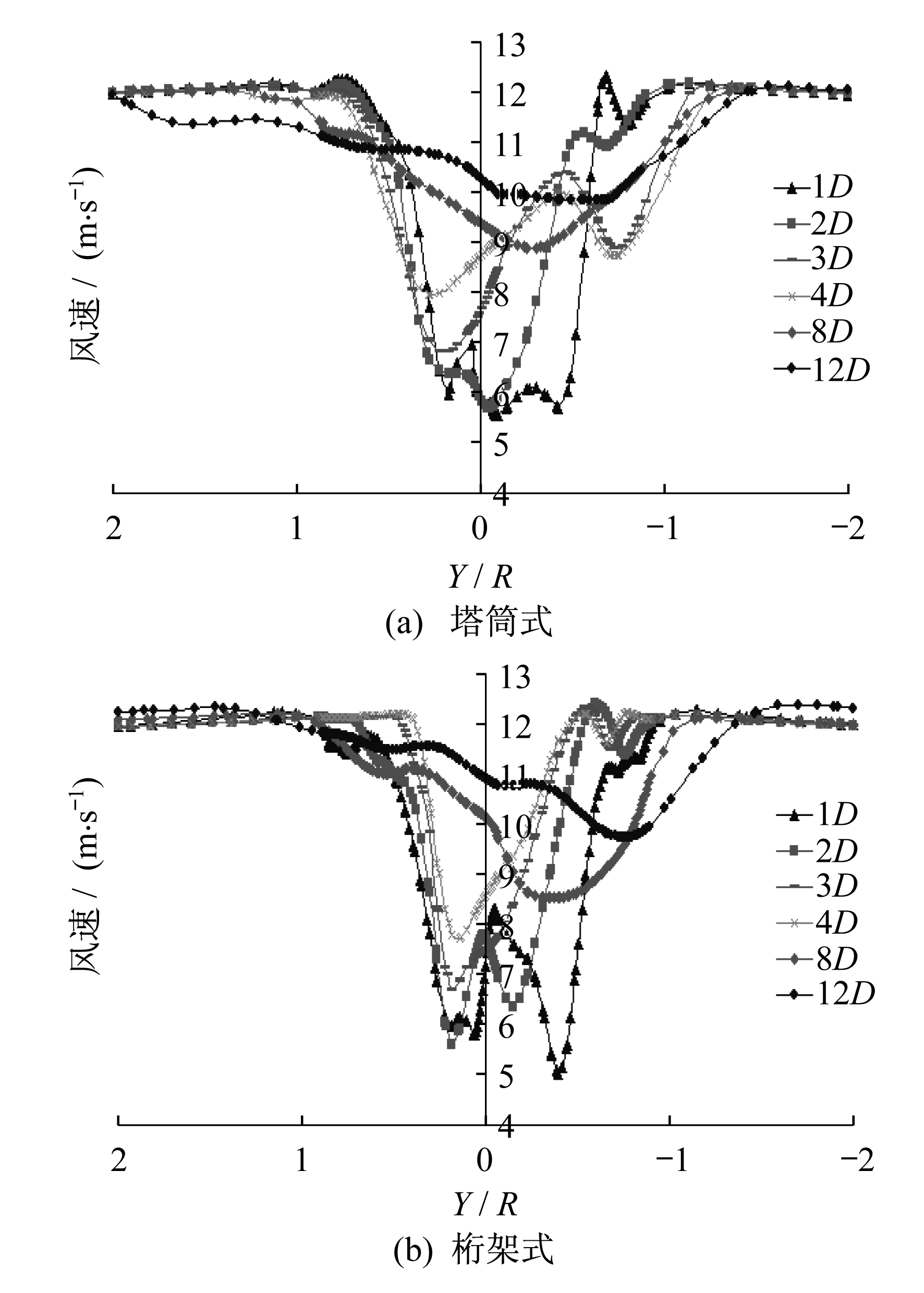
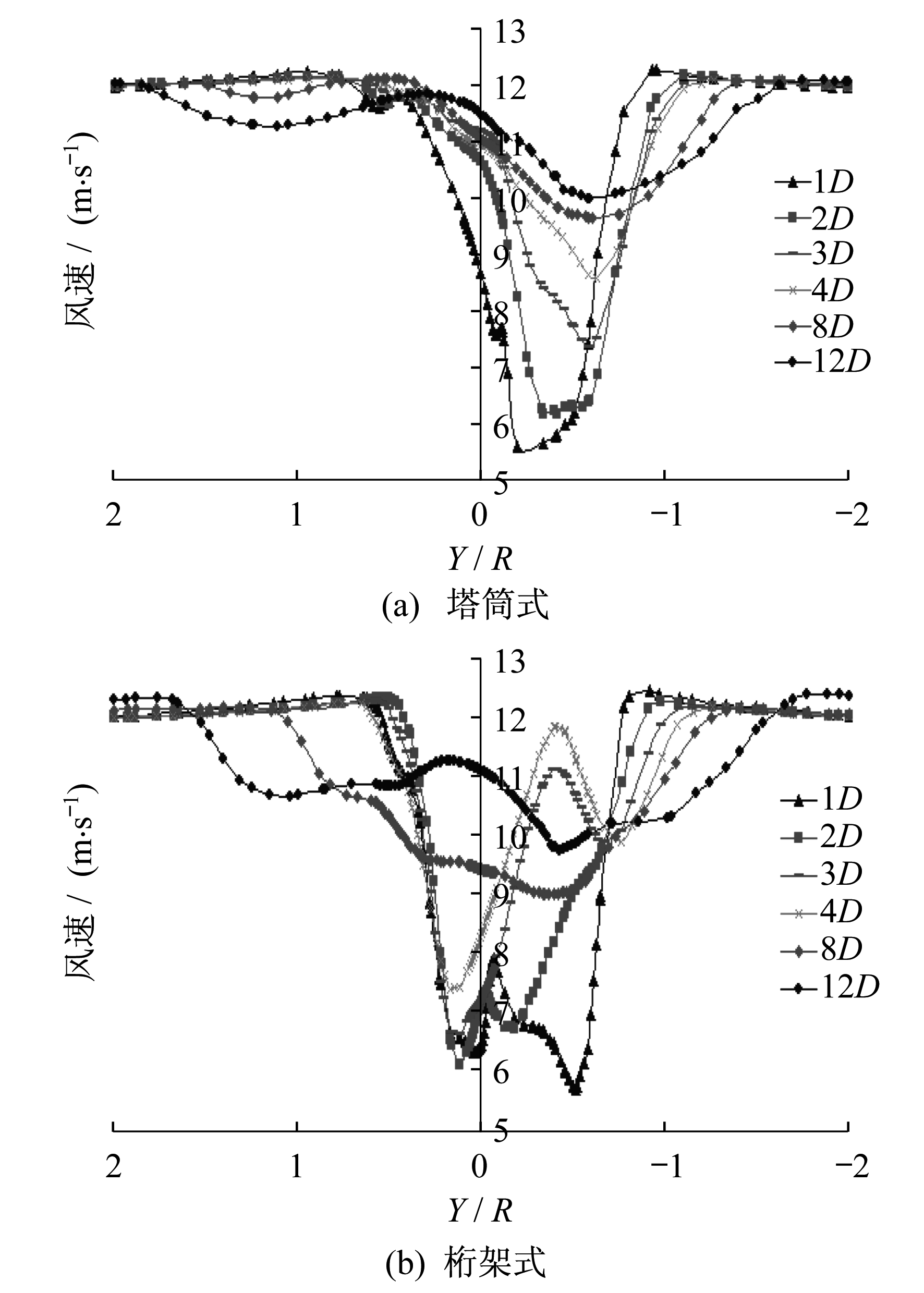
从图 11和图 12可以看出, 在风力机下游2倍风轮直径范围内, 塔影效应的影响是最大的, 但随着距离风力机越来越远, 塔影效应开始逐渐减小, 风速开始逐渐恢复[11]。在z=-40 m处下游8倍风轮直径处, 塔筒式风力机的流场风速已经恢复到来流风速的80%左右, 而桁架式风力机流场风速才恢复到来流风速的75%左右; 在z=-56.7 m处下游8倍风轮直径处, 塔筒式风力机的流场风速已经恢复到来流风速的85%左右, 而桁架式风力机流场风速才恢复到来流风速的80%左右; 在12倍风轮直径处, 塔筒式风力机的流场速度已经恢复到接近来流风速的90%, 桁架式也已经恢复到85%。由此表明, 在风力机下游相同距离处, 塔筒式风力机尾迹流场的最小速度总是略大于桁架式风力机流场的最小速度; 此外, 速度分布曲线的形状受塔架形状的影响, 这种影响在桁架式风力机上的表现要明显一点, 并且随着距离塔架越来越远, 塔架的形状对流场速度分布曲线的影响开始减弱。
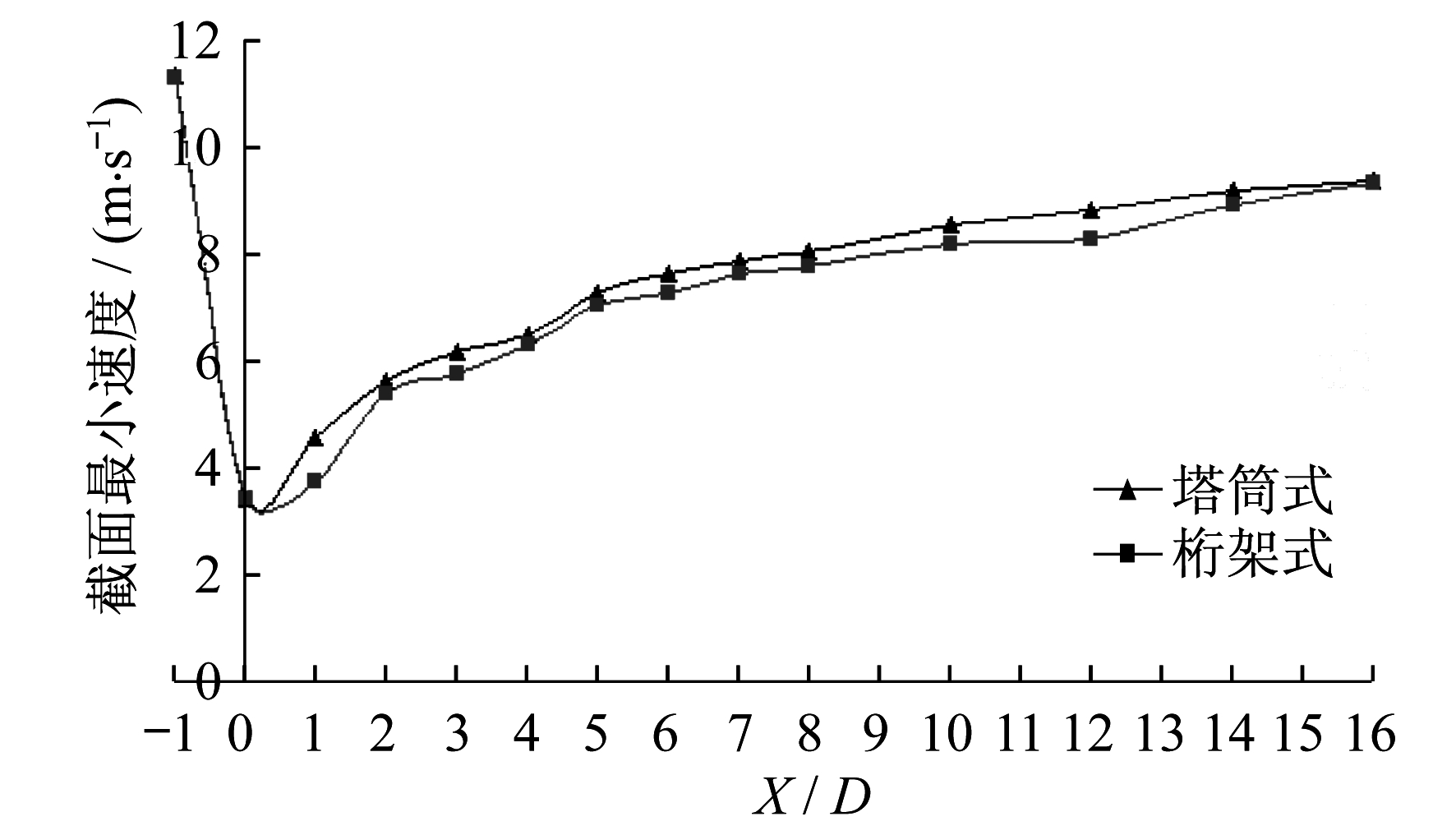
图 13为两种形式塔架不同截面的最小速度曲线。
从图 13可以看出, 无论是哪种形式的塔架, 在来流风到达风力机时, 风速都有很大的下降, 而随着距离风力机旋转平面越来越远, 两种形式塔架的风力机尾迹流场的最小速度都逐渐增大, 并且在0~5D的范围内风速增加的最快, 但桁架式风力机不同截面的最小速度始终略小于塔筒式风力机。
因此, 在选用桁架作为风力机塔架时, 风力机的布置间距要考虑略大于塔筒式风力机的布置间距。
3 结论
本文利用FLUENT软件对两种形式塔架的风力机整机进行了模拟分析, 在对塔影效应下的塔筒式和桁架式风力机受力情况、速度及湍流强度分布进行了对比分析后, 得出如下结论。
(1) 对比塔架表面所受的升力和阻力可以看出:对于塔筒式塔架的风力机, 每当叶片旋转到塔筒的前面时, 塔筒表面所受到的升力和阻力的大小和方向都发生急剧转变; 对于桁架式风力机, 桁架所受的升力和阻力明显小于塔筒所受的升力, 并且没有太大的波动和规律性。所以, 对于塔架本身来说, 桁架式的结构更安全一些。
(2) 对比风力机下游0.5倍风轮直径处两种形式塔架的速度和湍流强度曲线可以看出:塔筒式风力机的速度最小值和湍流强度最大值都出现在接近塔筒正后方的位置, 速度亏损的最大值约为30%, 湍流强度最大值约为40%;对于桁架式风力机。所以, 其速度最小值和湍流强度最大值出现的位置并不固定, 速度亏损最大值达到了70%, 湍流强度最大值则达到了120%, 明显大于塔筒式风力机。所以, 说明桁架对风力机尾迹的影响大于塔筒对风力机尾迹的影响。
(3) 对比两种形式塔架下游不同截面的风速曲线可以看出:在风力机下游2倍风轮直径范围内, 塔影效应的影响是最大的, 随着距离风力机越来越远, 塔影效应也开始逐渐减小, 风速开始逐渐恢复, 在0~5D范围内风速增加的速度最快, 并且在风力机下游相同距离处, 塔筒式风力机尾迹流场的最小速度总是略大于桁架式风力机的尾迹流场最小速度。所以, 桁架式风力机的布置间距要考虑略大于塔筒式风力机的布置间距。另外,速度分布曲线的形状受塔架形状的影响, 这种影响在桁架式风力机上的表现要明显一点, 并且随着距离塔架越来越远, 塔架的形状对流场速度分布曲线的影响开始减弱。
参考文献
-
[1]CHATTOT J J. Tower shadow modelization with helicoidal vortex method[J]. Computers & Fluids, 2008, 37(5): 499-504.
-
[2]LACKNER M A, DEVELDER N, SEBASTIAN T. On 2D and 3D potential flow models of upwind turbine tower interfere[J]. Computers & Fluids, 2013, 71(1): 375-379.
-
[3]REISO M, HAGEN T R, MUSKULUS M. A calibration method for downwind wake models accounting for the unsteady behaviour of the wind turbine tower shadow behindmonopole and truss tower[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 121: 29-38. DOI:10.1016/j.jweia.2013.07.016
-
[4]上风向风力机塔影效应的数值模拟研究[J]. 工程热物理学报, 2012, 33(19): 33-35.
-
[5]封晨颖.考虑塔影效应的风力机叶片气动载荷计算与数值模拟分析[D].湘潭: 湘潭大学, 2013.
-
[6]基于风剪切和塔影效应的风力机风速动态建模[J]. 太阳能学报, 2011, 32(8): 1238-1245.
-
[7]范忠瑶.风力机定常与非定常气动问题的数值模拟研究[D].保定: 华北电力大学, 2011.
-
[8]JONKMAN J, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5-MW reference wind turbine for off shore system development[R]. Technical Report NREL/TP-500-38060, 2009.
-
[9]MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149
-
[10]大型海上风力机尾迹区域风场分析[J]. 计算力学学报, 2012, 29(3): 327-332. DOI:10.7511/jslx20123006
-
[11]水平轴风力机近尾迹流场数值模拟[J]. 太阳能学报, 2010, 31(7): 1485-1490.