|
|
|
发布时间: 2019-12-10 |
|
|
|
|
收稿日期: 2018-11-26
基金项目: 国家自然科学基金青年科学基金(51607111)
中图法分类号: TM615
文献标识码: A
文章编号: 1006-4729(2019)06-0544-09
|
摘要
随着对能源利用效率要求的提高及日益激增的光伏数据, 传统的光伏预测方法已逐渐丧失优势。为了更加准确地进行光伏预测, 采用深度学习的框架, 并利用循环神经网络(RNN)中最重要的一个结构——长短时记忆网络(LSTM)对时间序列的强大处理能力进行了智能算法建模。由于LSTM具有“遗忘”与“更新”功能, 很好地解决了长序依赖问题, 从而使光伏预测在精度上有了质的变化, 预测速度也得到显著提升。
关键词
光伏预测; 深度学习算法; 循环神经网络; 长短时记忆网络
Abstract
With the increasing demand for energy efficiency and the pohtovoltaic data that is increasing coustantly, traditional PV forecasting methods have gradually lost their advantages.In order to make more accurate PV predictions, a deep learning framework is adopted.Due to the powerful processing power of time series, the most important structure in the recurrent neural network (RNN)—long-short-term memory network (LSTM) is used for intelligent algorithm modeling.Because LSTM has the functions of "forgetting" and "updating", it solves the problem of long-order dependence, which makes the PV prediction have a qualitative change in accuracy, and the prediction speed is also significantly improved.
Key words
photovoltaic power forecasting; deep learning algorithm; recurrent neural networks; long-short-term memory network
近年来, 光伏发电规模随着清洁能源的推广应用不断扩大。但由于光伏发电量随天气变化产生波动性, 不利于电力系统的安全经济运行, 使得光伏发电大规模并网遇到了阻碍[1]。准确地进行光伏出力预测是目前迫切需要解决的一大难题, 也是可再生能源电力系统的研究热点之一。为提高光伏预测的精度, 传统的算法一直在改进, 新的算法也不断地被提出, 主要可分为物理方法、统计方法和智能预测方法等几大类[2]。
物理方法是将光伏电池模型、逆变器模型以及光伏面板参数等整合起来进行建模预测。机理模型主要由太阳辐照方程和光电转化方程两大重要部分组成。由于物理方法存在受光伏组件影响较多的缺陷, 同时光伏电站的地理信息和气象信息较难获取, 所以导致模型的精确度无法满足要求, 在实际工程运用中会产生较大误差[3-4]。
统计方法需要大量的历史数据作为输入, 涉及概率统计和聚类等方法, 主要包括分类回归、时间序列、模糊聚类等方法。统计方法的不足在于, 光伏特征因素和光伏预测的函数关系很难直接从历史数据中提取, 使得预测结果与实际存在较大偏差, 因此在实际应用中很难得到普及[5-8]。
智能预测方法不同于传统的物理及统计方法, 需要从大量气象、光伏数据中通过模型的自学习能力进行数据挖掘, 寻找规律进行预测。目前, 光伏预测已从传统的浅层神经网络向更深层次、更多维度方向发展。之前智能预测方法基于训练函数拟合能力, 例如人工神经网络(Artificial Neural Network, ANN)[9]与支持向量机(Support Vector Machine, SVM)等。尽管此类方法在电力预测领域发挥了重要的作用, 但同样存在长时间序列记忆能力没有得到解决、多特征多维度的数据无法清晰表达、预测精度不理想等问题。基于此, HINTON G E等人提出了深度学习算法, 揭开了第一轮智能算法的探讨[10]。
2016年3月, 经过深度学习算法训练的AlphaGo击败了人类围棋顶尖高手; 2017年10月19日《自然》发表的一篇研究论文中指出:在无任何人类输入的条件下, AlphaGo Zero能够迅速自学围棋, 并以100:0的战绩击败“前辈”。自此掀起了深度学习算法的第二轮研究浪潮。目前, 深度学习算法多领域的应用已初见成效, 文字分析、图像处理、语音识别等方面都有突破性的创新[11]。在光伏预测领域, 深度学习算法仍处在起步阶段。多参数优化、神经网络结构调整、局部最优等是算法改进道路上亟待解决的难题[12]。
1 模型的可行性分析
深度学习算法的多神经网络层为其应对多特征的数据提供了有利结构, 而光伏预测的输入特征在时间尺度上的有序变化, 其中包含了太阳辐射强度、温度、气压等诸多特征, 两者的组合为光伏预测带来了新的可能。传统神经网络模型需要花费大量时间在数据预处理上, 包括数据清洗筛选、查漏补缺以及对影响因素较小的特征项进行剔除。这些看似智能的预测方法, 实则需要大量的人工干预, 只能算作是半智能算法; 而人为的特征筛选, 无法找到各个特征之间内在的隐藏联系, 从而造成了特征原始属性无法完整表达、错误估计特征量的潜在联系等问题。相对来说, 深度学习算法模型因其具有深度结构, 并且包含多层的隐层节点, 可以更好地保留特征间的隐藏属性, 使模型蕴含的信息能够完整表达。前期复杂的筛选工作由于模型的自学习能力得到有效简化, 干扰因素在权重与偏置的调整下逐渐弱化, 使得光伏预测研究真正走上了智能预测的道路。
人工提取特征属于浅层结构学习, 不具有普及性; 而深度学习算法则将光伏预测的特征进行深层次提取学习, 并在神经网络中进行复杂的特征变换, 即使在不同地区、不同时间也能捕捉到深层特征与隐藏信息, 使其在不同情形下能有相同预测效果[13]。循环神经网络(Recurrent Neural Network, RNN)作为深度学习中处理和预测序列数据的良好模型, 在各个领域都得到大量应用; 而长短时记忆网络(Long-Short-Term Memory, LSTM)作为RNN的一个重要结构, 在序列数据的长期记忆方面表现更为良好; 在光伏预测中, 辐照度、风速、温度、大气压力等都是随时间变化的序列数据, 理论上利用LSTM进行光伏预测切实可行。
2 基于深度学习的网络模型
得益于人工神经网络的研究, 深度学习模拟神经元运作方式对数据进行表征学习, 通过多隐藏层之间的联系建立起多层感知器的学习结构, 简单的数据形式在神经网络的作用下通过升维、降维获得了高层特征, 数据表达方式也得到了更新[14]。
2.1 LSTM模型
作为RNN中的一个重要结构, LSTM通过小模块的连接建立时间递归神经网络, 将时间序列中的延迟事件保存下来, 并在后续训练中进行提取。为了使子模块保存长期记忆, LSTM引进了核心结构“遗忘门”和“输入门”。遗忘门可以让循环神经网络遗忘无用的信息, 输入门可以输入补充最新的记忆, 两者的密切配合决定了信息的遗忘与保留[15]。
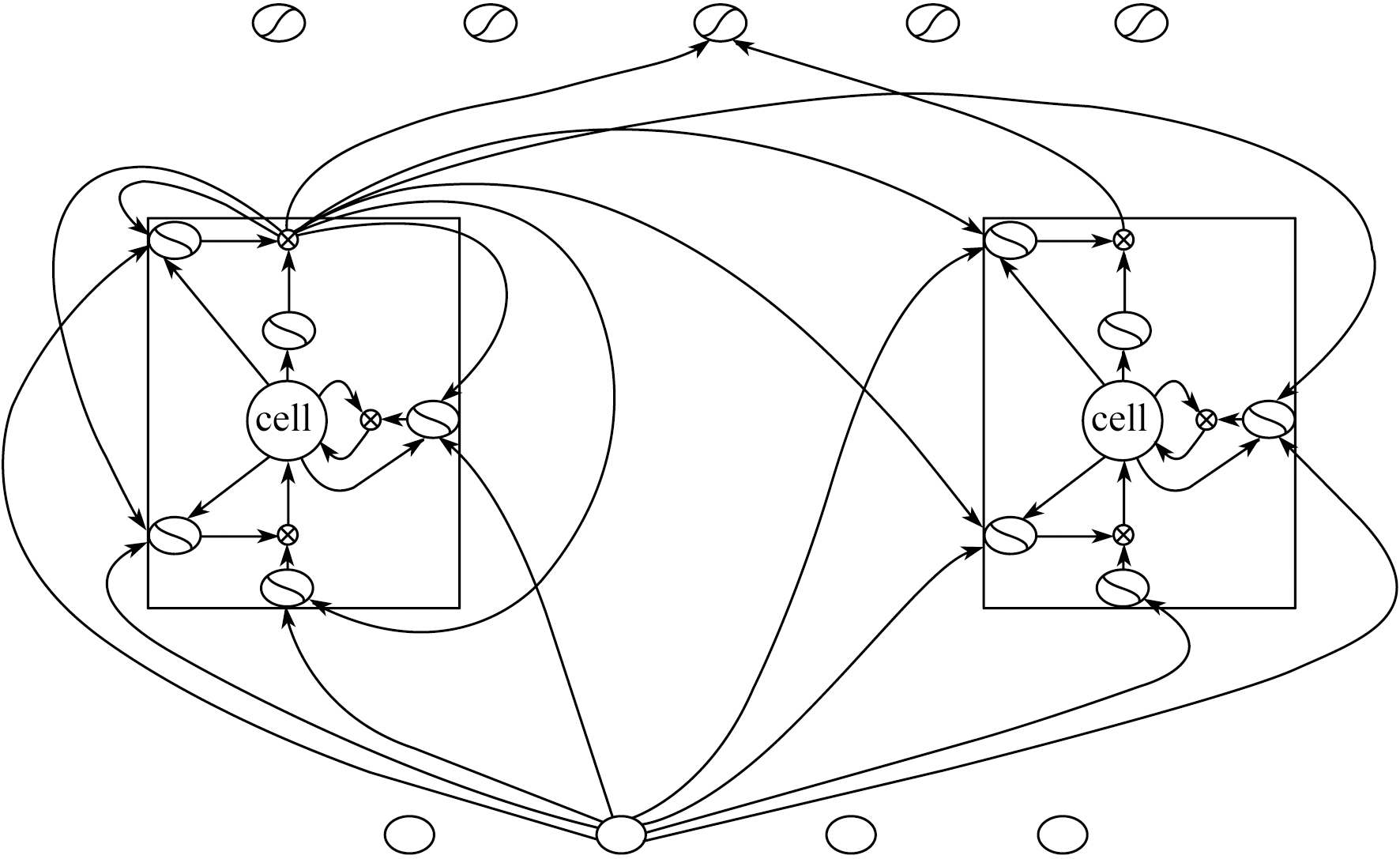
通过刻意的设计, LSTM将遗忘门层、输入门层、更新门层以及输出门层组合成为交互的层, 解决了长期依赖问题。LSTM的这些“门”结构组合处理器被称为cell。当输入进入cell中后, 根据判定规则决定信息的遗忘或保留。简单的一进二出的工作原理, 在反复运算下解决了神经网络中存在已久的长序依赖问题。此外, LSTM具有较高的普适性和灵活性。cell间的结构使得模型具有较长时间的记忆功能, 且使误差传递没有衰减, 当前信息即使在长时间后的训练中也能得到保存, 并对当前状态进行调整。
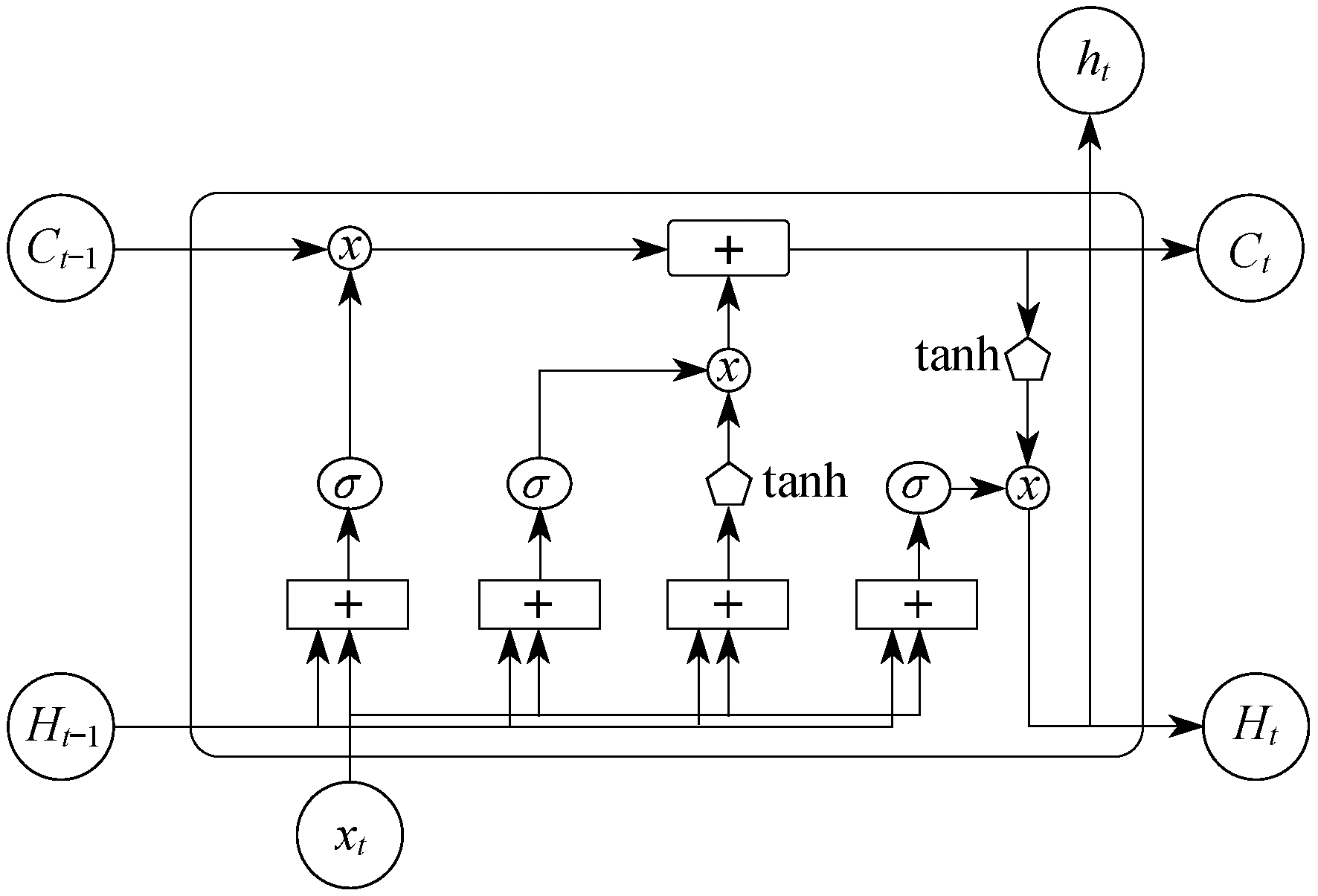
LSTM具体结构如图 1所示。图 1中, xt为t时刻输入; Ht-1为t-1时刻LSTM的输出; Ct-1为t-1时刻单元状态输出; Ht为t时刻输出; Ct为t时刻单元状态输出; ht为t时刻的信息保留; tanh为双切正切函数, 使输入值的取值范围为[-1, 1]。在特征相差明显时, 表现出良好效果并在循环过程中会不断扩大特征效果。
2.2 LSTM训练的核心思路
3 基于LSTM的光伏预测模型建立
3.1 输入数据预处理
光伏预测的难点之一在于前期的数据处理, 光伏电站的信息采集系统的稳定运行对预测过程影响巨大。数据不完整、缺失以及数据质量差是预测中首先要解决的问题。常用的数据修正方法是复杂度较低的K近邻补全算法, 即选取集中缺失数据的k个完整最近邻数据来进行补缺。序列数据最大特征就是相邻数据间具有相似性。若有某一段数据缺失, 根据其前后数据的连贯性, 选择辅助变量, 找到最邻近的k个样本, 求取平均值来替代缺失值。
首先, 利用欧式距离法判断远近, 公式为
| $ d\left(X_{i}, X_{j}\right)=\sqrt{\sum\limits_{r=1}^{m}\left(x_{i r}-x_{j r}\right)^{2}} $ | (1) |
式中:Xi={xi1, xi2, xi3, …, xim}——第i个样本点的前m维数据;
Xj={xj1, xj2, xj3, …, xjm}——第j个样本点的前m维数据;
xir——第i个样本点的第r维属性;
xjr——第j个样本点的第r维属性。
在进行上述判断后将序列归一化, 控制样本数据在[0, 1]的变化范围内。公式为
| $ y_{i}=\frac{x_{i}-\min (x)}{\max (x)-\min (x)} $ | (2) |
式中:yi——归一化后的输出值;
xi——输入值;
max(x)——此数组最大值;
min(x)——此数组最小值。
3.2 输入输出量的选择
在对输入数据进行预处理后, 如何选择合适的输入量及标签来使用神经网络进行训练, 是建立负荷预测模型中最为关键的一步。光伏预测中影响因素很多, 物理预测方法要求选取最为关键的因素作为输入量。利用深度学习的方式进行预测, 可有效避免数据筛选这项工作。此外, 由于LSTM网络特性, 在训练中对权重影响较小的特征项, 会在迭代中逐步被遗忘。具体输入特征如图 3所示。其中:xt为t时刻输入, it为t时刻输入门状态, ot为t时刻输出门状态, ft为t时刻遗忘门状态, ct为t时刻cell当前状态, ht为t时刻输出。
3.3 LSTM模型参数及相关函数选择
LSTM模型主要由5个参数进行约束, 包括神经网络层层数、步长、训练块大小、学习率、输入输出变量维数。神经网络层层数确定了网络的基本结构, 步长则表示每次训练的跨度, 训练块大小决定输入的大小, 学习率表示训练速率, 输入输出变量维数则确定了网络训练的输入输出之间的关系。
本文所用数据每天采样点数在80~150;多次实验后, 以40个历史数据作为一个batch用于预测, 每个历史数据具有39个特征值, 所以输入层维度为40×39, 输出层采用单输出LSTM的预测模型, 维数为1;隐藏层数目的多少决定了模型的拟合能力, 层数太少拟合效果差, 反之则会增加训练成本, 需要根据数据大小进行动态调整。
3.3.1 激活函数
目前, 训练RNN最有效的算法是反向传播算法。简而言之, LSTM网络通过反向传播, 以减少代价为导向, 调整各项参数。采用梯度下降算法, 沿梯度下降方向调整神经元之间的连接权重w和每个神经元本身的偏置b, 公式为
| $ \frac{\partial C}{\partial w}=(a-y) \sigma^{\prime}(z) x $ | (3) |
| $ \frac{\partial C}{\partial b}=(a-y) \sigma^{\prime}(z) $ | (4) |
式中:C——代价;
a——输出值;
y——实际值;
z——神经元的输入;
x——样本;
σ——激活函数。
若要训练收敛较快, 则选用的激活函数梯度就越大。
激活函数选取不当, 会造成梯度消失:当数值接近于正向∞, 求导之后就更小, 约等于零, 偏导为零。Sigmid会发生梯度消失, 很少采用; Tanh同样会梯度消失; ReLu相对较好, 不仅避免了梯度消失的问题, 而且起到了降维作用。
3.3.2 损失函数设计
损失函数(loss function)动态表达了训练过程中预测值f(x)与真实值Y的误差变化过程, 用L(Y, f(x))表示, 模型的好坏与损失函数密切相关。模型的结构风险函数θ*由经验风险项和正则项两部分组成, 损失函数作为经验风险的核心部分起着至关重要的作用。公式为
| $\theta^{*}=\arg \;\mathop {\min }\limits_\theta \frac{1}{N} \sum\limits_{i=1}^{N} L\left(y_{i}, f\left(x_{i}, \theta\right)+\lambda \Phi(\theta)\right)$ | (5) |
式中:θ——经验风险函数;
N——迭代次数。
损失函数度量的是预测值与真实值之间的差异, 通常写作L(y_, y), y_代表预测值, y代表真实值。目标函数可以看作是优化目标, 优化模型的最终目标是使目标函数最大或者最小。代价函数类似于目标函数, 区别在于:代价函数可以包含一些约束条件如正则项, 以准确率作为最终的评测指标, 而损失函数仅仅表达了训练过程中的误差变化。
3.3.3 隐藏层的确定
在确定神经网络模型的输入输出及隐藏层层数的参数后, 即可搭建神经网络基本架构。在其他条件不变的情况下, 隐藏层选取得越多, 网络数据处理能力和学习训练能力更好; 但神经元的增加, 带来的是模型复杂程度的增加, 若深度学习平台没有很好的硬件支撑, 训练速度将会变得十分缓慢。隐藏层节点的选取主要依靠经验, 在对模型进行无数次调参后, 确定最优参数。新模型一般会选用经验公式并配合试凑法进行隐藏层层数的选定, 经验公式为
| $l=\sqrt{m+n}+c \\ l=\sqrt{m n} \\ l=\sqrt{m n+1.679\;9 n+0.928\;8}$ | (6) |
式中:l——隐含层节点数;
m——输出层节点数;
n——输入层节点数;
c——调节常数, 取1~10。
光伏发电功率的预测模型输入层节点数为39, 输出层节点数为1, 则根据式(6)可初步确定出隐含层节点数在6~10之间。
3.3.4 预测效果评估
光伏发电系统在夜间无法运行, 发电功率为零。由于采用平均绝对误差(Mean Absolute Error, MAE)或者标准差(Standard Deviation, SD)会导致某些误差无法计算, 所以选用均方根误差(Root Mean Square Error, RMSE)进行讨论, 公式为
| $ \varepsilon_{\mathrm{RMSE}}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n}\left[\frac{\hat{P}(i)-p(i)}{C_{\mathrm{ap}, i}}\right]^{2}} $ | (7) |
式中:εRMSE——模型控制绝对误差的性能;
n——预测验证数据个数;
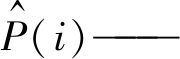 风电功率的预测值;
风电功率的预测值;
p(i)——风电功率的实际值;
i——预测点序列编号;
Cap, i——输出序列最大值。
4 算例分析
本文采用美国佛罗里达州Cocoa地区某光伏电站发电数据。该地区位于西五区, 北纬28.39°, 西经80.46°, 海拔高度为12 m。光伏组件采用施耐德Micro03036, 光伏面板倾斜率为28.5°, 光伏模块方位角为180°, 时间为2011年1月21日至2012年3月4日, 采样周期为5 min, 共计39 040条数据。由于一年中太阳日出日落的时间不同, 所以每天采样的时间点也不同, 加上采集器的数据丢失, 每天的时间点在80~150不等。常规的神经网络对数据清洗要求很高, 数据质量对实验结果的误差影响很大。本文对数据只进行了初步的筛选, 数据空缺采用K邻补全法进行了填补, 这是智能算法的优势之一。在大数据的支撑下, 一方面缺失或者采集错误的数据占比非常小, 另一方面算法本身对数据不好的特征项会相应的减少其影响因子。这些都使得LSTM对数据的依赖仅仅体现在数量上。
4.1 预测过程
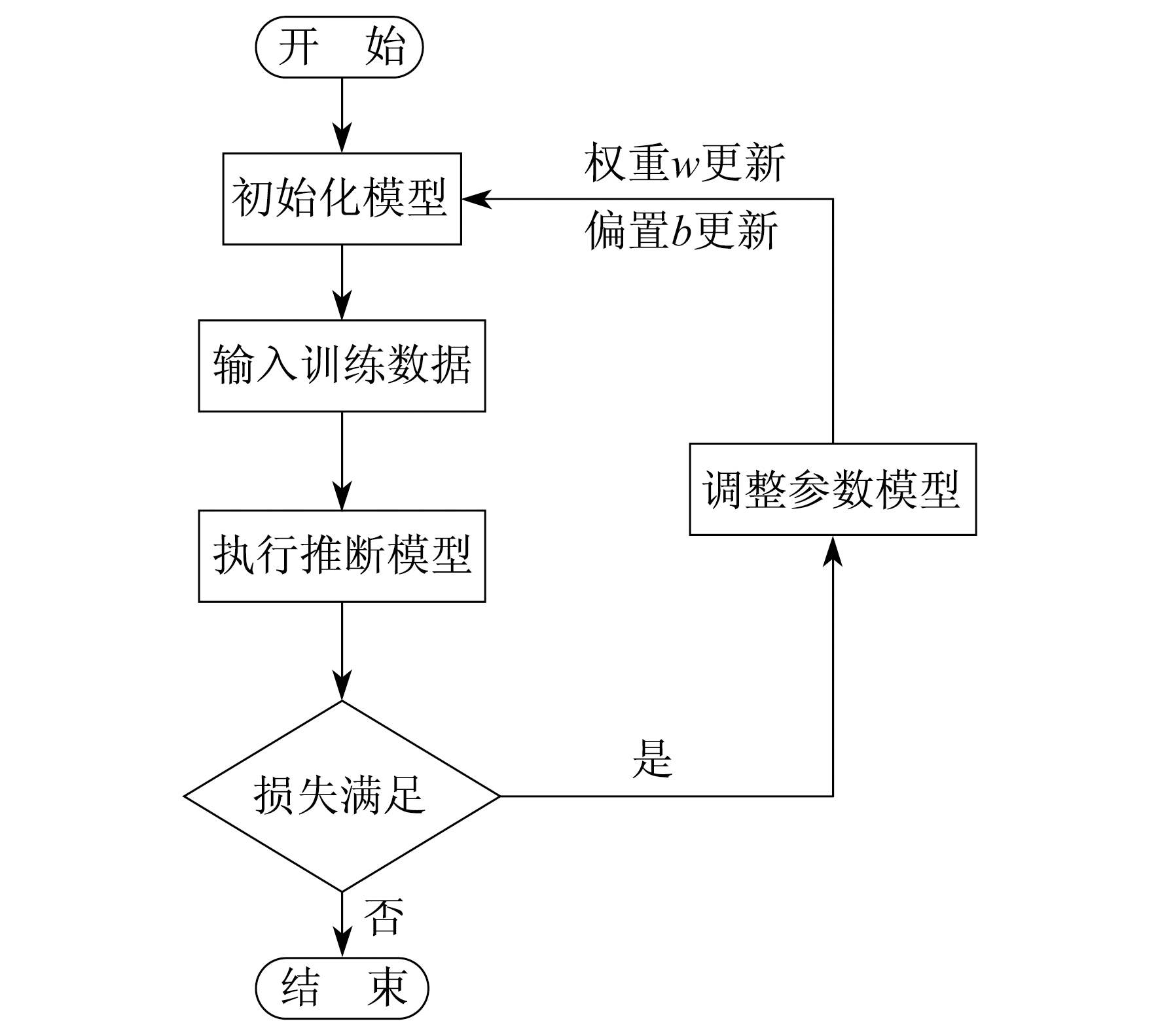
本文对Cocoa地区某一光伏电站进行建模。首先, 对光伏发电系统的发电原理进行研究, 并对光伏发电输出功率的影响因素进行分析; 其次, 在综合考虑物理方法及统计方法的基础上, 利用深度学习算法进行预测, 取得最优功率预测模型; 最后, 对预测得到的数据与实测数据进行对比分析。模型计算流程图如图 4所示。
(1) 首先研究光伏发电技术的原理, 熟悉光伏发电系统的构成和运行方式。太阳辐照度、温度、风速、云团等相关天气条件是影响光伏发电的主要因素, 通过分析光伏电站的历史发电数据及气象数据, 最终确定影响输出功率的主要影响因素和次要影响因素。
(2) 39 000条数据中, 取前35 000条作为训练集, 后4 000条作为测试集。经预处理后, 将水平面辐射和NWP气象数据(温度、湿度、气溶胶浓度和云量等相关天气条件)、发电站的逆变器、电池等硬件的数据信息(电池温度, 伏安特性等)作为特征输入, 并将光伏电站的历史实测发电量作为输出, 代入LSTM深度神经网络中, 对区域内光伏电站进行功率预测训练, 建立相应的深度学习模型。
(3) 在建立深度学习模型后, 选取测试集中某一天作为对照样本。假设这一天共采集了n条数据, 那么需要向前一天借m条(m为训练集大小, 即训练块大小)数据; 以a+m条(其中0≤a≤n-1, a∈Z)为一个训练块, 建立连续n个初始输入矩阵, 具体为
| $ \left[ {\begin{array}{*{20}{c}} {\left[\begin{array}{cccc} a_{0,0} & a_{0,1} & \cdots & a_{0,38} \\ a_{1,0} & a_{1,1} & \cdots & a_{1,38} \\ \vdots & \vdots & & \vdots \\ a_{m-1,0} & a_{m-1,1} & \cdots & a_{m-1,38} \end{array}\right]}\\ {\left[\begin{array}{cccc} a_{1,0} & a_{1,1} & \cdots & a_{1,38} \\ a_{2,0} & a_{2,1} & \cdots & a_{2,38} \\ \vdots & \vdots & & \vdots \\ a_{m, 0} & a_{m, 1} & \cdots & a_{m, 38} \end{array}\right]}\\ {\begin{array}{*{20}{c}} \vdots & \vdots & \vdots \end{array}}\\ {\left[\begin{array}{cccc} a_{n-1,0} & a_{n-1,1} & \cdots & a_{n-1,38} \\ a_{n, 0} & a_{n, 1} & \cdots & a_{n, 38} \\ \vdots & \vdots & & \vdots \\ a_{n+m-1,0} & a_{n+m-1,1} & \cdots & a_{n+m-1,38} \end{array}\right]} \end{array}} \right]$ |
对应输出矩阵为
| $ \left[\begin{array}{c} y_{m-1} \\ y_{m} \\ \vdots \\ y_{n+m-1} \end{array}\right] $ |
模型内部运行流程如下。
每个LSTM包含了3个输入, 即上一时刻的单元状态、上一时刻LSTM的输出和当前时刻输入。遗忘门用来计算哪些信息需要忘记, 通过ReLu函数处理后变为0~∞的值, 数值大小表示保留程度(0表示全部忘记), 于是有
ft=σ(Wf·[ht-1, xt]+bf)
式中:ft——ReLu损失函数;
Wf, bf——遗忘门的偏置项。
若输入层维度、隐藏层维度、状态维度分别为dx, dh, dc, 得到Wf=dc(dh+dx)。
输入门引入两部分新的信息到cell中, 第一部分为需保存信息, 即
it=σ(Wi·[ht-1, xt]+bi)
第二部分为产生的新信息, 即
| $ \tilde{c}_{t}=\tanh \left(W_{c} \cdot\left[h_{t-1}, x_{t}\right]+b_{c}\right) $ |
两部分信息的组合获得一个新记忆。当前状态由遗忘门输入、前一个cell状态及上输入门组成, 公式为
| $ c_{t}=f_{t} c_{t-1}+i_{t} \tilde{c}_{t} $ |
输出门通过ReLu函数计算输出信息, 再与当前单元状态值计算得到
ot=σ(Wo·[ht-1, xt]+bo)
ht=ottanh(ct)
4.2 超参数影响分析
隐藏层表示模型含有的LSTM层数。隐藏层数越多, 函数能够更加准确拟合。但层数过多会造成训练量急速上升, 影响训练速度。不同隐藏层层数训练效果对比如表 1所示。经多次尝试, 最优训练参数确定隐藏层层数为10时, 此时均方根误差可以达到0.001级别, 明显好于9层、11层一个数量级。
表 1
不同隐藏层层数训练效果对比
| 隐藏层层数 | 训练块大小 | 步长 | 学习率 | 迭代次数 | 均方根误差 |
| 9 | 50 | 40 | 0.0006 | 2000 | $0.0110 \sim 0.0140$ |
| 10 | 50 | 40 | 0.0006 | 2000 | $0.0011 \sim 0.0040$ |
| 11 | 50 | 40 | 0.0006 | 2000 | $0.0130 \sim 0.0210$ |
训练块大小表示输入矩阵的大小。在神经网络训练过程中, 合理范围内增大训练块大小, 可以让内存利用更加有效。同时, 跑完一次全数据集所需的迭代次数减少, 这也意味着处理速度会得到有效的提升。训练块大小越大, 下降方向可以更加容易地确定, 训练震荡会稳定在合理范围内; 但若盲目增大训练块大小, 内存容量会被迅速占用, 造成数据溢出, 程序崩溃。不同训练块大小训练效果对比如表 2所示。由表 2可知, 当训练块大小在50左右时, 训练效果最好。
表 2
不同训练块大小训练效果对比
| 隐藏层层数 | 训练块大小 | 步长 | 学习率 | 迭代次数 | 均方根误差 |
| 10 | 30 | 40 | 0.0006 | 2000 | $0.0021 \sim 0.0140$ |
| 10 | 50 | 40 | 0.0006 | 2000 | $0.0011 \sim 0.0040$ |
| 10 | 70 | 40 | 0.0006 | 2000 | $0.0310 \sim 0.0620$ |
| 10 | 100 | 40 | 0.0006 | 2000 | $0.0700 \sim 0.0760$ |
步长表示每次训练移动的长度。步长移动距离越短, 搜索过程中越不会错过最优解, 但代价是花费大量时间, 收敛缓慢, 容易陷入局部最优。步长过长, 每次偏移过大, 会造成永远都找不到真正的最小值。对于深度越高的神经网络, “平滑区”会越来越多, 局部最小点也会越来越多。没有合适的算法, 很容易陷入某个局部最小值里去。不同步长训练效果对比如表 3所示。由表 3可以看出, 步长持续增大, 训练结果反而越差, 这也意味着步长存在最适区间, 超过或者低于这个区间, 对训练结果都会有极大影响。
表 3
不同步长训练效果对比
| 隐藏层层数 | 训练块大小 | 步长 | 学习率 | 迭代次数 | 均方根误差 |
| 10 | 50 | 20 | 0.0006 | 2000 | $0.0017 \sim 0.0530$ |
| 10 | 50 | 40 | 0.0006 | 2000 | $0.0011 \sim 0.0040$ |
| 10 | 50 | 60 | 0.0006 | 2000 | $0.0021 \sim 0.0550$ |
| 10 | 50 | 80 | 0.0006 | 2000 | $0.0280 \sim 0.0630$ |
学习率表示模型的训练速度。不同的学习率, 模型的效果相差甚远。一般而言, 学习率可先从一个较大的值开始, 如0.1, 这样可以实现快速调试。学习率太大会造成损失爆炸, 太小损失又会训练无反应, 选择一个合适的学习率可以更快的让训练达到稳态。不同学习率训练效果对比如表 4所示。通过表 4可以发现, 随着学习率的提高, 预测精度也随之提高。
表 4
不同学习率训练效果对比
| 隐藏层层数 | 训练块大小 | 步长 | 学习率 | 迭代次数 | 均方根误差 |
| 10 | 50 | 40 | 0.06000 | 2000 | $0.0017 \sim 0.0530$ |
| 10 | 50 | 40 | 0.00600 | 2000 | $0.0051 \sim 0.0080$ |
| 10 | 50 | 40 | 0.00060 | 2000 | $0.0081 \sim 0.0055$ |
| 10 | 50 | 40 | 0.00006 | 2000 | $0.0028 \sim 0.0063$ |
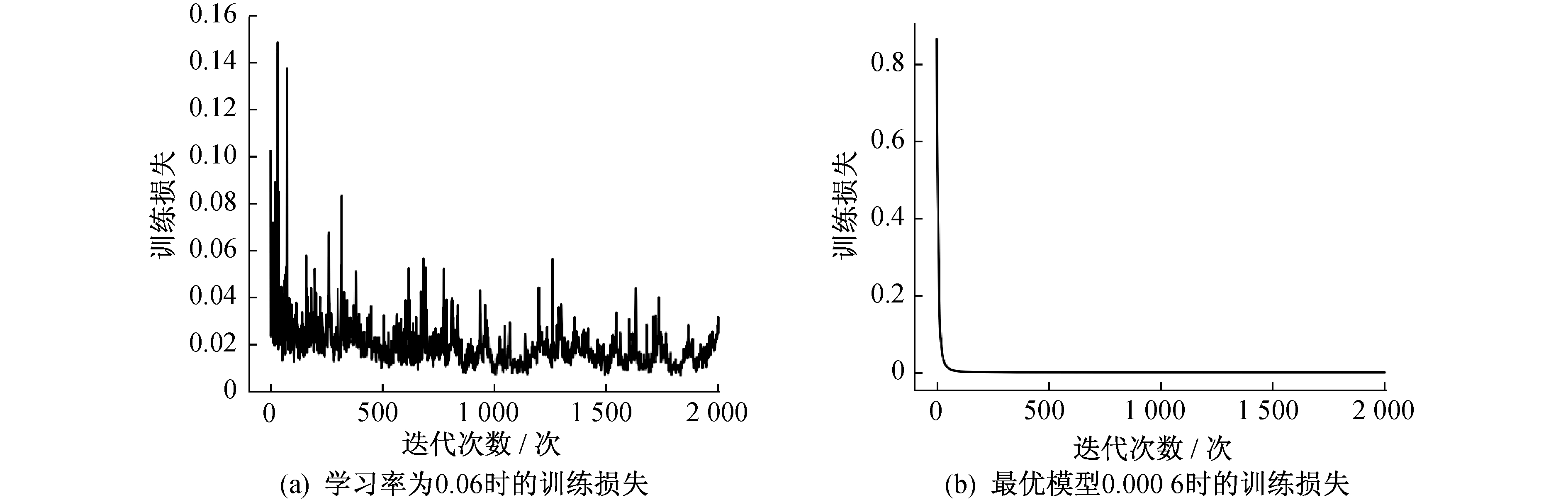
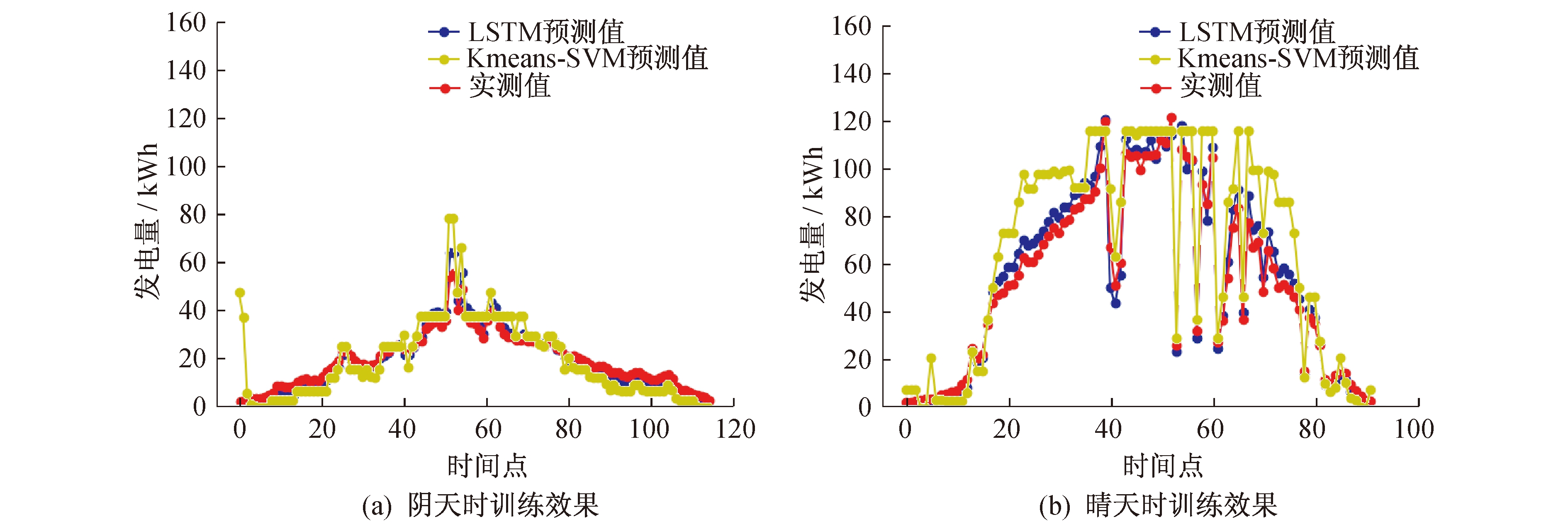
不同学习率训练损失对比如图 5所示。由图 5可知, 学习率太低, 训练过程震荡明显。随着学习率的提高, 训练损失趋于稳定, 达到0.000 6时已符合训练目的。学习率为0.06时, 两种天气训练输出与最优解如图 6所示。
经过一系列对参数的调整发现, 当训练块大小为50, 隐藏层层数为10, 步长为40, 学习率为0.000 6, 迭代次数为2 000次时, 可获得相对最优预测模型。
4.3 对照算法
4.3.1 Kmeans-SVM对照算法
VAPNIK V N等人在1995年就提出了支持向量机(Support Vector Machine, SVM)算法, 随后, VAPNIK V N将不敏感损失函数ε引入, 使得算法扩展到解决非线性回归问题[16]。具体如下。
对于给定样本集dataset={(x1, y1)(x2, y2), …, (xn, yn)}, xi∈Rd为输入值, yi∈R为目标值, i=1, 2, 3, …, n。其中Rd为d维的实数集。通过线性回归函数f(x)=wT+b来拟合样本(xi, yi), 采用ε不敏感损失函数, 可得
| $|y-f(x)|_{\varepsilon}= \\ \left\{\begin{array}{l}0 \quad|y-f(x)|<\varepsilon \\ |y-f(x)|-\varepsilon \quad|y-f(x)| \geqslant \varepsilon\end{array}\right.$ | (8) |
引入惩罚因子C, 松弛因子ξi和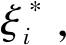 则最优化问题为
则最优化问题为
| $\min \frac{1}{2}\|w\|^{2}+C \sum\limits_{i=1}^{n}\left(\xi_{i}+\xi_{i}^{*}\right) \\ \mathrm{s. t.} f\left(x_{i}\right)-y_{i} \leqslant \varepsilon+\xi_{i} \\ y_{i}-f\left(x_{i}\right) \leqslant \varepsilon+\xi_{i}^{*} \\ \xi_{i} \geqslant 0, \xi_{i}^{*} \geqslant 0, i=1,2,3, \cdots, n$ | (9) |
引入拉格朗日乘子αi和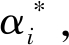 使用核函数k(x, xi), 整理得到回归模型为
使用核函数k(x, xi), 整理得到回归模型为
| $ f(x)=\sum\limits_{i=1}^{n}\left(\alpha_{i}^{*}-\alpha_{i}\right) k\left(x, x_{i}\right)+b $ | (10) |
由于自身的局限性, 仅利用SVM算法解决复杂的预测问题远远不够。为了提高预测算法的精度, 本文采用Kmeans算法对输入特征量进行聚类。其目的就是寻找K个质心来最小化平方误差。将样本集划分成K个簇, 簇的质心Ci的均值向量为
| $ \mu_{i}=\frac{1}{\left|C_{i}\right|} \sum\limits_{x \in C_{i}} x $ | (11) |
4.3.2 Kmeans-SVM模型结构
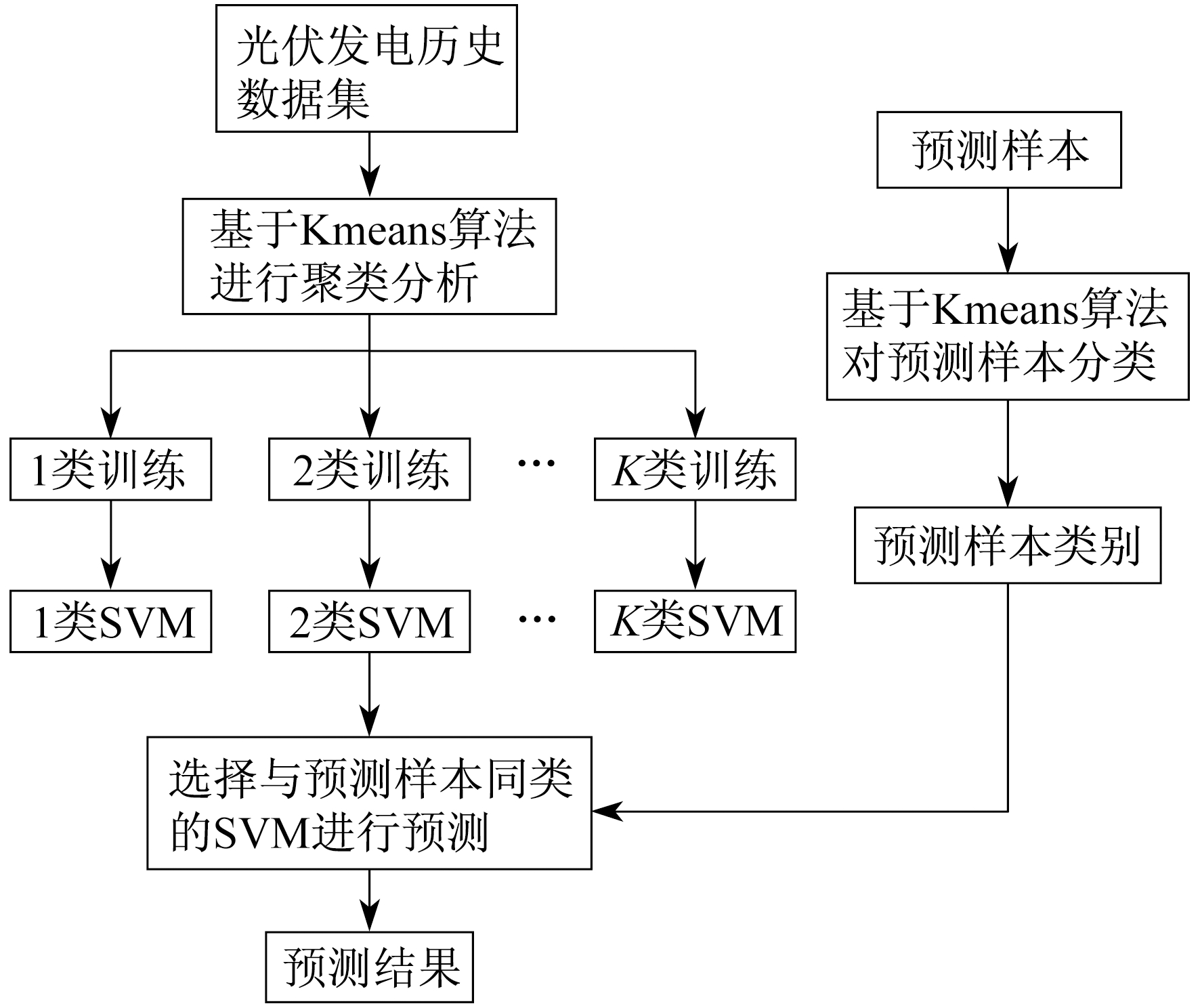
Kmeans-SVM预测模型框架如图 7所示。基于对光伏发电功率影响因素的分析, 选出以下4个参数作为训练样本:光伏组件输出的直流电流I, 直流电压U, 组件温度T, 发电功率P。
该预测模型将当前时刻的I(t), U(t), T(t), P(t), t时刻上一时刻的I(t-1), U(t-1), T(t-1), P(t-1)作为训练集的输入特征, 下一时刻的发电功率P(t+1)作为训练样本的目标, 则当前时刻的训练样本可表示为[t, I(t), U(t), T(t), P(t)k, I(t-1), U(t-1), T(t-1), P(t-1), P(t+1)]。
该预测模型可表示为
P(t+1)=mod[t, I(t), U(t), T(t), P(t),
I(t-1), U(t-1), T(t-1),
P(t-1)]
以连续两个时刻的4个参数值作为样本特征, 使用Kmeans算法把连续两个时刻光伏发电状态相近的样本归为一类, 以时刻t为特征可使归为一类的样本尽量在相邻时段。该模型先基于Kmeans算法对样本集进行聚类分析, 将样本集分成K个训练集(此处的K值通过经验法、试凑法确定), 将与预测样本同类的训练样本输入SVM来预测下一时刻的发电功率。
4.3.3 Kmeans-SVM与LSTM模型对比
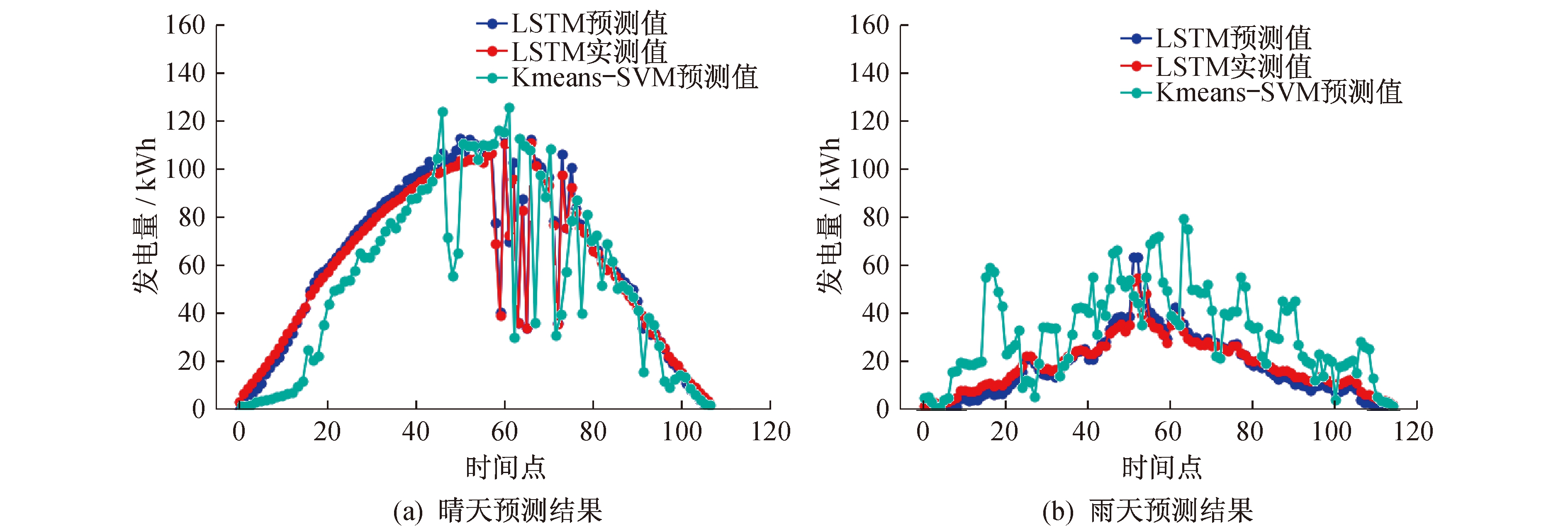
本文以美国佛罗里达州Cocoa地区某光伏电站实测数据为例, 从历史数据样本中选取晴天(2011年7月5日)、雨天(2011年6月29日)两种典型天气类型作为训练测试集对Kmeans-SVM算法光伏发电功率预测模型进行训练, 并将所得结果与LSTM算法模型预测得到的结果进行对比。图 8展示了晴天与雨天两种情况下Kmeans-SVM预测值、LSTM算法预测值与实测值的对比曲线。尽管Kmeans-SVM算法经过了聚类处理, 但结果表明LSTM算法模型的预测精度更为准确。
两种天气预测模型的误差统计结果如表 5所示。由表 5可知, Kmeans-SVM算法相较于LSTM算法预测模型两种天气预测误差分别提高了22倍和18倍。由此可见, 即使拥有K-means算法的数据分类能力以及SVM算法的泛化能力, Kmeans-SVM光伏功率预测模型与LSTM模型相比, 仍然有着巨大差距。Kmeans-SVM无需考虑数据的天气类别的情况, 即可对训练样本进行聚类分析, 但LSTM却拥有无需进行数据分类的处理方式。
表 5
两种天气预测模型的误差统计
| 天气类型 | $E_{\mathrm{RMSE}}$ | |
| Kmeans-SVM模型预测 | LSTM预测模型 | |
| 晴天 | 0.053 | 0.0023 |
| 雨天 | 0.093 | 0.0047 |
5 结语
本文从光伏预测物理原理出发, 分析了影响光伏预测的主要因素; 在对时间序列数据进行分析后, 基于LSTM的工作原理, 证明LSTM神经网络对负荷预测的适用性; 然后进行输入输出维度的选择, 建立了基于LSTM的负荷预测模型。最后与Kmeans-SVM算法进行比较发现, LSTM模型直接省去前期复杂的数据筛选预处理过程, 使得模型的局限性得到了极大的改善, 证明了基于深度学习的LSTM神经网络的负荷预测模型具有更高的精确度和更好的适用性。
参考文献
-
[1]光伏功率预测技术[J]. 电力系统自动化, 2016, 40(4): 140-151. DOI:10.7500/AEPS20150711003
-
[2]基于S-BGD和梯度累积策略的改进深度学习方法及其在光伏出力预测中的应用[J]. 电网技术, 2017, 41(10): 3292-3299.
-
[3]MA T, YANG H G, LU L. Solar photovoltaic system modeling and performance prediction[J]. Renewable & Sustainable Energy Reviews, 2014, 36(8): 304-315.
-
[4]LORENZ E, HURKA J, HEINEMANN D, et al. Irradiance forecasting for the power prediction of grid-connected photo-voltaic systems[J]. IEEE Journal of Selected Topics in.
-
[5]Applied Earth Observations & Remote Sensing, 2009, 2(1): 2-10.
-
[6]光伏发电出力的条件预测误差概率分布估计方法[J]. 电力系统自动化, 2015, 39(16): 8-15. DOI:10.7500/AEPS20141017007
-
[7]聚类分析在光伏发电量预测中的应用研究[J]. 可再生能源, 2017, 35(5): 696-701. DOI:10.3969/j.issn.1671-5292.2017.05.010
-
[8]基于提升小波-BP神经网络的光伏阵列短期功率预测[J]. 可再生能源, 2017, 35(4): 566-571. DOI:10.3969/j.issn.1671-5292.2017.04.015
-
[9]基于GA-ELM神经网络的日前电价预测[J]. 上海电力学院学报, 2018, 34(1): 90-94.
-
[10]基于改进的GABP神经网络光伏发电短期出力预测[J]. 上海电力学院学报, 2018, 34(1): 9-13.
-
[11]HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507. DOI:10.1126/science.1127647
-
[12]DAHL G E, YU D, DENG L, et al. Application of pretrained deep neural networks to large vocabulary conversational speech recognition[J]. IEEE Transactions on Audio, Speech & Language Processing, 2012, 20(1): 30-42.
-
[13]GOODFELLOW L, BENGIO Y S, GOURVILLE A. Deep learning[M]. Cambridge: Mit Press, 2016: 240-249.
-
[14]基于深度学习的超短期光伏精细化预测模型研究[J]. 电力建设, 2017, 38(6): 28-35. DOI:10.3969/j.issn.1000-7229.2017.06.005
-
[15]基于深度学习的个性化智能导学平台的研究[J]. 网络安全技术与应用, 2018(5): 34-35. DOI:10.3969/j.issn.1009-6833.2018.05.020
-
[16]改进型LSTM变形预测模型研究[J]. 江西理工大学学报, 2018, 39(5): 48-54.
-
[17]基于EMD和ABC-SVM的光伏并网系统输出功率预测研究[J]. 电力系统保护与控制, 2015, 43(21): 86-92.