|
|
|
发布时间: 2019-12-10 |
|
|
|
|
收稿日期: 2019-04-02
基金项目: 国家自然科学基金(61573239);上海市重点科技攻关计划项目(14110500700);上海市电站自动化技术重点实验室项目(13DZ2273800)
中图法分类号: TM46
文献标识码: A
文章编号: 1006-4729(2019)06-0553-09
|
摘要
当电网电压不平衡时, 交流侧的电流会出现不对称, 有功功率和无功功率在模块化多电平变流器(MMC)外部出现二次波动, 严重影响系统的稳定性和电源质量。因此, 在电网电压不平衡条件下控制MMC是非常必要的。针对电网电压不平衡状态下的MMC交流侧三相电流不对称、有功功率二次脉动、无功功率二次脉动问题, 对这3种控制目标下的参考电流分别进行了求解, 并制定了传统PI控制、滑模控制、无源控制等控制策略。最后, 在MATLAB /Simulink平台上仿真并比较3种控制策略的优缺点。
关键词
电网电压不平衡; 模块化多电平变流器; PI控制; 滑模控制; 无源控制
Abstract
When the grid voltage is unbalanced, the current on the AC side will be asymmetrical, and the active power and reactive power will cause secondary fluctuations outside the MMC, which seriously affects the stability of the system and the power quality.Therefore, it is necessary to control the MMC under grid voltage imbalance.For MMC under grid voltage imbalance, AC phase three-phase current is asymmetrical, active power secondary pulsation, and reactive power secondary pulsation problem.Firstly, the reference currents of the three control targets are solved separately, and the control strategies such as conventional PI controller, sliding mode controller and passive controller are formulated.Finally, the advantages and disadvantages of various controls are compared on the MATLAB/Simulink platform.
Key words
grid voltage imbalance; modular multilevel converter; PI control; sliding mode control; passivity based control
在中国, 地理空间的能源和电力消耗分配极不合理, 模块化多电平变流器型高压直流输电(Modular Multilevel Converter based High Voltage Direct Current, MMC-HVDC)输电容量大、谐波特性好, 因此MMC-HVDC在中国电网建设中具有极其重要的意义。目前, 生态环境问题已成为中国不平衡和不协调发展的突出问题。这要求我们加快用新能源替代不可再生能源的步伐, 促进能源生产和消费革命。在能源生产过程中, 发展方向主要体现在清洁能源, 特别是新能源的大规模开发和利用上。近年来, 越来越多的风能和太阳能等新能源的利用率不断提高。截至2017年底, 中国的总装机容量为17.8亿kW, 位居世界第一, 是1978年的30多倍。电力供应结构逐步清洁化, 清洁能源装机容量从1978年的30.3%增加到2017年的37.5%[1]。然而, 风能和太阳能等可再生能源的特点是随机性、间歇性和波动性。大规模、高比例的新能源的渗入, 会对传统的交流输电造成污染, 而MMC-HVDC输电可以减少谐波侵入, 保证电能质量, 很好地解决这些问题。它为建设具有广泛互联、智能互动、灵活性和安全性的新一代电力系统奠定了基础[2]。
当电网电压不平衡时, MMC-HVDC的交流侧会发生不平衡, 有功功率和无功功率也会出现二次脉动, 严重影响着电能质量[3-4]。文献[5-6]提出了滑模控制, 文献[7-10]提出了无源控制。滑模和无源控制各有优缺点, 但相比较传统PI控制都有各自优势。本文针对电网电压不平衡条件下的MMC的控制策略, 提出了滑模和无源的控制策略, 并与传统PI控制进行比较, 以验证本文所提控制策略的优越性。
1 电网电压不平衡条件下MMC的控制目标
当电网电压不平衡时, 由于电网与MMC之间存在Y/Δ变压器, 不存在零序分量, 因此交流侧的输出电压和输出电流可以分解[3-4]为
| $ \left\{\begin{aligned} u_{\mathrm{sj}}=& U^{+} \cos \left(\omega t+\theta^{+}+\gamma\right)+\\ & U^{-} \cos \left(-\omega t+\theta^{-}+\gamma\right) \\ i_{\mathrm{sj}}=& I^{+} \cos \left(\omega t+\varphi^{+}+\gamma\right)+\\ & I^{-} \cos \left(-\omega t+\varphi^{-}+\gamma\right) \end{aligned}\right. $ | (1) |
式中:U+, U-, I+, I-——正、负序电压、电流的幅值;
ω——交流侧电网角频率;
θ+, θ-, φ+, φ-——正、负序电压及电流的初相角;
γ——相角差。
同样地, 将式(1)中的MMC的网侧电压和电流变换到dq两相旋转坐标下, 可以得到
| $ \left\{\begin{array}{l} U_{\mathrm{s}}=U_{\mathrm{s}}^{+}+U_{\mathrm{s}}^{-} \\ I_{\mathrm{s}}=I_{\mathrm{s}}^{+}+I_{\mathrm{s}}^{-} \end{array}\right. $ | (2) |
式中:
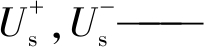 usj在dq坐标系的正、负序分量;
usj在dq坐标系的正、负序分量;
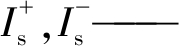 isj在dq坐标系下的分量。
isj在dq坐标系下的分量。
根据瞬时功率理论, MMC交流侧的瞬时功率可以表示为
| $ \begin{array}{c} S=\frac{2}{3}\left(u_{\mathrm{s}}^{+} \mathrm{e}^{\mathrm{j} \theta_{1}}+u_{\mathrm{s}}^{-} \mathrm{e}^{-\mathrm{j} \theta_{1}}\right)\left(i_{\mathrm{s}}^{+} \mathrm{e}^{\mathrm{j} \theta_{1}}+i_{\mathrm{s}}^{-} \mathrm{e}^{-\mathrm{j} \theta_{1}}\right)= \\ P_{\mathrm{s} 0}+P_{\mathrm{s} 2 \sin } \cos (2 \omega t)+P_{\mathrm{s} 2 \cos } \sin (2 \omega t)+ \\ Q_{\mathrm{s} 0}+Q_{\mathrm{s} 2 \mathrm{sin}} \cos (2 \omega t)+Q_{\mathrm{s} 2 \cos } \sin (2 \omega t) \end{array} $ | (3) |
式中:θ1——d轴和q轴之间的夹角;
Ps0, Qs0——有功功率、无功功率的直流量;
Ps2sin, Qs2sin——有功功率、无功功率的2次波动量的正弦分量的幅值;
Ps2cos, Qs2cos——有功功率、无功功率的2次波动量的余弦分量的幅值。
将式(3)整理成矩阵形式为
| $ \left[ \begin{matrix} {{P}_{\text{s0}}} \\ {{P}_{\text{s2sin}}} \\ {{P}_{\text{s2cos}}} \\ {{Q}_{\text{s0}}} \\ {{Q}_{\text{s2sin}}} \\ {{Q}_{\text{s2cos}}} \\ \end{matrix} \right]\text{=}\frac{3}{2}\left[ \begin{matrix} u_{\text{s}d}^{+} & u_{\text{s}q}^{+} & u_{\text{s}d}^{-} & u_{\text{s}q}^{-} \\ u_{\text{s}q}^{-} & -u_{\text{s}d}^{-} & -u_{\text{s}q}^{+} & u_{\text{s}d}^{+} \\ u_{\text{s}d}^{-} & u_{\text{s}q}^{-} & u_{\text{s}d}^{+} & u_{\text{s}q}^{+} \\ u_{\text{s}q}^{+} & -u_{\text{s}d}^{+} & u_{\text{s}q}^{-} & -u_{\text{s}d}^{-} \\ -u_{\text{s}d}^{-} & -u_{\text{s}q}^{+} & u_{\text{s}d}^{+} & u_{\text{s}q}^{+} \\ u_{\text{s}q}^{-} & -u_{\text{s}d}^{-} & u_{\text{s}d}^{+} & u_{\text{s}q}^{+} \\ \end{matrix} \right]\left[ \begin{matrix} i_{\text{s}d}^{+} \\ i_{\text{s}q}^{+} \\ i_{\text{s}d}^{-} \\ i_{\text{s}q}^{-} \\ \end{matrix} \right] $ | (4) |
根据电网电压发生不平衡所造成的影响, 可将外部控制目标分为3个:交流侧电流为三相对称交流电; 有功功率无脉动; 无功功率无脉动。依照式(4), 不同的控制目标得到不同的参考电流, 并由此进行控制。
交流侧电流为三相对称交流电(控制目标1), 也即电流中无负序分量, 即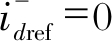 和
和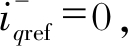 根据式(4)可以得到
根据式(4)可以得到
| $ \left\{\begin{array}{l} i_{d \mathrm{ref}}^{+}=\frac{2}{3} \frac{u_{\mathrm{s}q}^{+} P_{\mathrm{s} 0}+u_{\mathrm{s} d}^{+} Q_{\mathrm{s} 0}}{u_{\mathrm{s}d}^{+^{2}}+u_{\mathrm{s}q}^{+^{2}}} \\ i_{q \mathrm{ref}}^{+}=\frac{2}{3} \frac{u_{\mathrm{s}q}^{+} P_{\mathrm{s} 0}+u_{\mathrm{s}d}^{+} Q_{\mathrm{s} 0}}{u_{\mathrm{s}d}^{+^{2}}+u_{\mathrm{s}q}^{+^{2}}} \end{array}\right. $ | (5) |
有功功率无脉动(控制目标2), 也即消除有功功率2倍频的波动。提取式(4)的前4列, 可得
| $\left[\begin{array}{c}P_{\mathrm{s} 0} \\ P_{\mathrm{s} 2 \mathrm{sin}} \\ P_{\mathrm{s} 2 \cos } \\ Q_{\mathrm{s} 0}\end{array}\right]=\frac{3}{2}\left[\begin{array}{cccc}u_{\mathrm{s} d}^{+} & u_{\mathrm{s}q}^{+} & u_{\mathrm{s}d}^{-} & u_{\mathrm{s}q}^{-} \\ u_{\mathrm{s} q}^{-} & -u_{\mathrm{s}d}^{-} & -u_{\mathrm{s}q}^{+} & u_{\mathrm{s}d}^{+} \\ u_{\mathrm{s}d}^{-} & u_{\mathrm{s}q}^{-} & u_{\mathrm{s}d}^{+} & u_{\mathrm{s}q}^{+} \\ u_{\mathrm{s}q}^{+} & -u_{\mathrm{s}d}^{+} & u_{\mathrm{s}q}^{-} & -u_{\mathrm{s}d}^{-}\end{array}\right]\left[\begin{array}{c}i_{\mathrm{s}d}^{+} \\ i_{\mathrm{s}q}^{+} \\ i_{\mathrm{s} d}^{-} \\ i_{\mathrm{s}q}^{-}\end{array}\right]$ | (6) |
消除有功功率的波动, 即满足有功功率的正弦2倍频与余弦2倍频都为零, 即Ps2sin=0, Ps2cos=0, 可得到该控制目标下的电流给定值为
| $ \left\{ {\begin{array}{l} i_{d \mathrm{ref}}^{+}=\frac{2}{3}\left(\frac{u_{\mathrm{s} d}^{+}}{D_{1}} P_{\mathrm{s} 0}+\frac{u_{\mathrm{s} q}^{+}}{D_{2}} Q_{\mathrm{s} 0}\right) \\ i_{q\mathrm{ref}}^{+}=\frac{2}{3}\left(\frac{u_{\mathrm{s}q}^{+}}{D_{1}} P_{\mathrm{s} 0}-\frac{u_{\mathrm{s} d}^{+}}{D_{2}} Q_{\mathrm{s} 0}\right) \\ i_{d \mathrm{ref}}^{-}=\frac{2}{3}\left(-\frac{u_{\mathrm{s} d}^{-}}{D_{1}} P_{\mathrm{s} 0}+\frac{u_{\mathrm{s}q}^{-}}{D_{2}} Q_{\mathrm{s} 0}\right) \\ i_{q \mathrm{ref}}^{-}=\frac{2}{3}\left(-\frac{u_{\mathrm{s} q}^{-}}{D_{1}} P_{\mathrm{s} 0}-\frac{u_{\mathrm{s} d}^{-}}{D_{2}} Q_{\mathrm{s} 0}\right) \end{array}} \right. $ | (7) |
其中,
| $ \begin{array}{l} D_{1}=u_{\mathrm{s} d}^{+^{2}}+u_{\mathrm{s} q}^{+^{2}}-u_{\mathrm{s} d}^{-2}-u_{\mathrm{s} d}^{-^{2}} \\ D_{2}=u_{\mathrm{s} d}^{+^{2}}+u_{\mathrm{s} q}^{+^{2}}+u_{\mathrm{s} d}^{-2}+u_{\mathrm{s} d}^{-2} \end{array} $ |
无功功率无脉动(控制目标3), 也即消除无功功率2倍频的波动。提取式(4)的1, 4, 5, 6列, 可得到表达式如下
| $ \left[ {\begin{array}{*{20}{c}} {{P_{{\rm{s0}}}}}\\ {{Q_{{\rm{s0}}}}}\\ {{Q_{{\rm{s2sin}}}}}\\ {{Q_{{\rm{s2cos}}}}} \end{array}} \right]{\rm{ = }}\frac{3}{2}\left[ {\begin{array}{*{20}{c}} {u_{{\rm{s}}d}^ + }&{u_{{\rm{s}}q}^ + }&{u_{{\rm{s}}d}^ - }&{u_{{\rm{s}}q}^ - }\\ {u_{{\rm{s}}q}^ + }&{ - u_{{\rm{s}}d}^ + }&{u_{{\rm{s}}q}^ - }&{ - u_{{\rm{s}}d}^ - }\\ { - u_{{\rm{s}}d}^ - }&{ - u_{{\rm{s}}q}^ - }&{u_{{\rm{s}}d}^ + }&{u_{{\rm{s}}q}^ + }\\ {u_{{\rm{s}}q}^ - }&{ - u_{{\rm{s}}d}^ - }&{u_{{\rm{s}}q}^ + }&{ - u_{{\rm{s}}d}^ + } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {i_{{\rm{s}}d}^ + }\\ {i_{{\rm{s}}q}^ + }\\ {i_{{\rm{s}}d}^ - }\\ {i_{{\rm{s}}q}^ - } \end{array}} \right]$ | (8) |
此控制目标下无功功率的2次谐波为零, 即Qs2sin=0, Qs2cos=0, 可求解出此控制目标下给定电流的表达式为
| $ \left\{ {\begin{array}{*{20}{c}} {i_{d \mathrm{ref}}^{+}=\frac{2}{3}\left(\frac{u_{\mathrm{s} d}^{+}}{D_{2}} P_{\mathrm{s} 0}+\frac{u_{\mathrm{s}q}^{+}}{D_{1}} Q_{\mathrm{s} 0}\right)}\\ {i_{q \mathrm{ref}}^{+}=\frac{2}{3}\left(\frac{u_{\mathrm{s} q}^{+}}{D_{2}} P_{\mathrm{s} 0}-\frac{u_{\mathrm{s}d}^{+}}{D_{1}} Q_{\mathrm{s} 0}\right)}\\ {i_{d \mathrm{ref}}^{-}=\frac{2}{3}\left(-\frac{u_{\mathrm{s}d}^{-}}{D_{2}} P_{\mathrm{s} 0}+\frac{u_{\mathrm{s} q}^{-}}{D_{1}} Q_{\mathrm{s} 0}\right)}\\ {i_{q \mathrm{ref}}^{-}=\frac{2}{3}\left(-\frac{u_{\mathrm{s}q}^{-}}{D_{2}} P_{\mathrm{s} 0}-\frac{u_{\mathrm{s} d}^{-}}{D_{1}} Q_{\mathrm{s} 0}\right)} \end{array}} \right. $ | (9) |
根据上述3个控制目标, 分别得到在各个目标下的给定电流, 再将该电流作为不同原理设计的控制器的参考值来达到控制目的。
2 控制策略制定
2.1 控制原理比较
2.1.1 PI控制
PI控制器已存在多年, 由于其结构简单、稳定性好、运行可靠且调整方便, 已成为工业控制的主要技术之一。其控制量通过线性组合给定值和实际值之间的偏差而形成。控制部分主要由比例和积分两个部分组成。其中:比例调节的作用是将系统出现的偏差减小, 比例作用越大, 调节速度越快, 误差减小, 但过大的比例会使系统的稳定性降低; 积分环节可使系统消除稳态误差, 其作用越大, 稳态性越好, 但动态响应速度越慢。
2.1.2 滑模控制
2.1.3 基于欧拉-拉格朗日模型的无源控制
无源控制(Passivity Based Control, PBC)是ORTEGA R等人提出的非线性反馈能量控制方法。无源系统的能量从初始时间到当前时间增加不超过外部注入能量的总和, 也就是说, 无源系统的运动问题伴随着能量损失。PBC控制利用输出反馈使得闭环系统特性表现为一无源映射, PBC使用输出反馈使闭环系统特征成为无源映射, 其使用欧拉-拉格朗日(Euler-Lagrange, EL)数学模型, 通过能量整形和阻尼注入(Energy Shaping and Damping Injection, ESDI), 注入合适的阻尼项, 配置系统能量耗散特性方程中的无功分量“无功力”, 迫使系统总能量跟踪预期的能量函数, 使闭环控制系统无源, 以保证系统的稳定性, 并使得被控对象的输出渐近收敛到期望值[7-9]。
2.2 双dq变换的PI控制策略制定
对于电网电压不平衡条件下MMC的PI控制策略, 通常是建立在正负序旋转坐标系下的数学模型, 在正负序系统各自使用PI控制方法。
MMC在dq坐标轴上对应着各相序的数学模型。其正序模型和负序模型分别为
| $ \left\{\begin{array}{l} u_{\mathrm{s}d}^{+}+\omega L_{0} i_{q}^{+}-R_{0} i_{d}^{+}-L_{0} \frac{\mathrm{d} i_{d}^{+}}{\mathrm{d} t}=u_{d}^{+} \\ u_{\mathrm{s}q}^{+}+\omega L_{0} i_{d}^{+}-R_{0} i_{q}^{+}-L_{0} \frac{\mathrm{d} i_{q}^{+}}{\mathrm{d} t}=u_{q}^{+} \end{array}\right. $ | (10) |
| $ \left\{\begin{array}{l} u_{s d}^{-}+\omega L_{0} i_{q}^{-}-R_{0} i_{d}^{-}-L_{0} \frac{d i_{d}^{-}}{d t}=u_{d}^{-} \\ u_{s q}^{-}+\omega L_{0} i_{d}^{-}-R_{0} i_{q}^{-}-L_{0} \frac{d i_{\mathrm{q}}^{-}}{d t}=u_{\mathrm{q}} \end{array}\right. $ | (11) |
为消除耦合项, 实现各相的单独控制, 设计的正序控制器和负序控制器分别为
| $ \left\{\begin{array}{l} y_{d+}=k_{\mathrm{p}+}\left(i_{d+}^{*}-i_{d+}\right)+k_{\mathrm{i}+} \int\left(i_{d+}^{*}-i_{d+}^{\mathrm{p}}\right) \mathrm{d} t \\ y_{q+}=k_{\mathrm{p}+}\left(i_{d+}^{*}-i_{d+}\right)+k_{\mathrm{i}+} \int\left(i_{d+}^{*}-i_{d+}\right) \mathrm{d} t \end{array}\right. $ | (12) |
| $\left\{\begin{array}{l}y_{d-}=k_{\mathrm{p}-}\left(i_{d-}^{*}-i_{d-}\right)+k_{\mathrm{i}-} \int\left(i_{d-}^{*}-i_{d-}^{\mathrm{p}}\right) \mathrm{d} t \\ y_{q-}=k_{\mathrm{p}-}\left(i_{d-}^{*}-i_{d-}\right)+k_{\mathrm{i}-} \int\left(i_{d-}^{*}-i_{d-}\right) \mathrm{d} t\end{array}\right.$ | (13) |
式中:yd+, yq+, yd-, yq-——正负序PI控制器的输出量;
kp+, ki+, kp-, ki-——正负序PI控制器系数。
将正负序PI控制器的输出量与解耦量相加, 得到PI控制器的数学模型为
| $ \left\{\begin{aligned} u_{d+}=& k_{\mathrm{p}+}\left(i_{d+}^{*}-i_{d+}\right)+\\ & k_{\mathrm{i}+} \int\left(i_{d+}^{*}-i_{d+}\right) \mathrm{d} t+\omega L_{0} i_{q+}+u_{\mathrm{s} d+} \\ u_{q+}=& k_{\mathrm{p}+}\left(i_{d+}^{*}-i_{d+}\right)+\\ & k_{\mathrm{i}+} \int\left(i_{d+}^{*}-i_{d+}\right) \mathrm{d} t-\omega L_{0} i_{d+}+u_{\mathrm{s} q+} \end{aligned}\right. $ | (14) |
| $\left\{\begin{aligned} u_{d-}=& k_{\mathrm{p}-}\left(i_{d-}^{*}-i_{d-}\right)+\\ & k_{\mathrm{i}-} \int\left(i_{d-}^{*}-i_{d-}\right) \mathrm{d} t+\omega L_{0} i_{q-}+u_{\mathrm{s}d-} \\ u_{q-}=& k_{\mathrm{p}-}\left(i_{d-}^{*}-i_{d-}\right)+\\ & k_{\mathrm{i}-} \int\left(i_{d-}^{*}-i_{d-}\right) \mathrm{d} t-\omega L_{0} i_{d-}+u_{\mathrm{s} q-} \end{aligned}\right.$ | (15) |
将交流侧三相电压电流进行正负序分离得到的dq坐标系下的正负序分量, 并将根据控制目标得到的正负序电流参考值代入设计的PI控制器内, PI控制器的输出量与环流控制器相配合对MMC进行控制。
2.3 SMC控制策略制定
相比其他控制策略, SMC控制策略在两相静止坐标系中进行控制, 其最大的优势在于可同时实现有功功率和无功功率无脉动的控制目标。
在电网电压不平衡条件下, 网侧的瞬时功率可以表示为
| $ \left\{\begin{array}{l} P=P_{0}+P_{\mathrm{c} 2}+P_{\mathrm{s} 2} \\ Q=Q_{0}+Q_{\mathrm{c} 2}+Q_{\mathrm{s} 2} \end{array}\right. $ | (16) |
式中:P0, Q0——P和Q的平均值;
Ps2, Ps2, Qs2, Qs2——有功功率余弦量、有功功率正弦量、无功功率余弦量、无功功率正弦量的2倍频波动量。
将式(16)写成矩阵形式为
| $ \left[ {\begin{array}{*{20}{c}} {{P_0}}\\ {{P_{{\rm{c2}}}}}\\ {{P_{{\rm{s2}}}}}\\ {{Q_0}}\\ {{Q_{{\rm{c2}}}}}\\ {{Q_{{\rm{s2}}}}} \end{array}} \right]=\frac{3}{2}\left[\begin{array}{cccc} u_{\mathrm{s} \alpha}^{+} & u_{\mathrm{s} \beta}^{+} & u_{\mathrm{s} \alpha}^{-} & u_{\mathrm{s} \beta}^{-} \\ 0 & 0 & u_{\mathrm{s} \alpha}^{+} & u_{\mathrm{s} \beta}^{+} \\ u_{\mathrm{s} \alpha}^{-} & u_{\mathrm{s} \beta}^{-} & 0 & 0 \\ u_{\mathrm{s} \beta}^{+} & -u_{\mathrm{s} \alpha}^{+} & u_{\mathrm{s} \beta}^{-} & -u_{\mathrm{s} \alpha}^{-} \end{array}\right]\left[\begin{array}{c} i_{\mathrm{s} \alpha}^{+} \\ i_{\mathrm{s} \beta}^{+} \\ i_{\mathrm{s} \alpha}^{-} \\ i_{\mathrm{s} \beta}^{-} \end{array}\right] $ | (17) |
对网侧有功功率、无功功率分别进行求导, 可以得到
| $ \left\{\begin{array}{l} \frac{\mathrm{d} P}{\mathrm{d} t}=\frac{3}{2}\left(\frac{\mathrm{d} u_{\mathrm{s} \alpha}}{\mathrm{d} t} i_{\mathrm{s} \alpha}+\frac{\mathrm{d} i_{\mathrm{s} \alpha}}{\mathrm{d} t} u_{\mathrm{s} \alpha}+\frac{\mathrm{d} u_{\mathrm{s} \beta}}{\mathrm{d} t} i_{\mathrm{s} \beta}+\frac{\mathrm{d} i_{\mathrm{s} \beta}}{\mathrm{d} t} u_{\mathrm{s} \beta}\right) \\ \frac{\mathrm{d} Q}{\mathrm{d} t}=\frac{3}{2}\left(\frac{\mathrm{d} u_{\mathrm{s} \alpha}}{\mathrm{d} t} i_{\mathrm{s} \alpha}+\frac{\mathrm{d} i_{\mathrm{s} \alpha}}{\mathrm{d} t} u_{\mathrm{s} \alpha}+\frac{\mathrm{d} u_{\mathrm{s} \beta}}{\mathrm{d} t} i_{\mathrm{s} \beta}+\frac{\mathrm{d} i_{\mathrm{s} \beta}}{\mathrm{d} t} u_{\mathrm{s} \beta}\right) \end{array}\right. $ | (18) |
静止坐标系下电流的导数为
| $ \left\{\begin{array}{l} \frac{\mathrm{d} i_{\mathrm{s} \alpha}}{\mathrm{d} t}=\frac{1}{L_{0}}\left(v_{\alpha}-R_{0} I_{\mathrm{s} \alpha}-u_{\mathrm{s} \alpha}\right) \\ \frac{\mathrm{d} i_{\mathrm{s} \beta}}{\mathrm{d} t}=\frac{1}{L_{0}}\left(v_{\beta}-R_{0} I_{\mathrm{s} \beta}-u_{\mathrm{s} \beta}\right) \end{array}\right. $ | (19) |
将式(19)代入式(18), 得到有功功率和无功功率表达式为
| $ \left\{\begin{array}{c} \frac{\mathrm{d} P}{\mathrm{d} t}=\frac{3}{2 L_{0}}\left(u_{\mathrm{s} \alpha} v_{\alpha}+u_{\mathrm{s} \beta} v_{\beta}\right)-\frac{3}{2 L_{0}} u_{\mathrm{s}}^{2}+ \\ \frac{3}{2}\left(i_{\mathrm{s} \alpha} \frac{\mathrm{d} u_{\mathrm{s} \alpha}}{\mathrm{d} t}+i_{\mathrm{s} \beta} \frac{\mathrm{d} u_{\mathrm{s} \beta}}{\mathrm{d} t}\right)-\frac{R_{0}}{L_{0}} P \\ \frac{\mathrm{d} Q}{\mathrm{d} t}=\frac{3}{2 L_{0}}\left(u_{\mathrm{s} \beta} v_{\alpha}+u_{\mathrm{s} \alpha} v_{\beta}\right)+ \\ \frac{3}{2}\left(i_{\mathrm{s} \alpha} \frac{\mathrm{d} u_{\mathrm{s} \beta}}{\mathrm{d} t}-i_{\mathrm{s} \beta} \frac{\mathrm{d} u_{\mathrm{s} \alpha}}{\mathrm{d} t}\right)-\frac{R_{0}}{L_{0}} Q \end{array}\right. $ | (20) |
在电网电压不平衡时, 电压在两相静止坐标系下可以表示为正序分量与负序分量之和, 即
| $ \boldsymbol{u}_{\mathrm{s}}=\left[\begin{array}{c} u_{\mathrm{s} \alpha}^{+}+u_{\mathrm{s} \alpha}^{-} \\ u_{\mathrm{s} \beta}^{+}+u_{\mathrm{s} \beta}^{-} \end{array}\right] $ | (21) |
式(21)可写为
| $ \left\{\begin{array}{l} u_{\mathrm{s} \alpha}^{+}=U_{\mathrm{s}}^{+} \cos \left(\omega_{1} t+\theta^{+}\right) \\ u_{\mathrm{s} \beta}^{+}=U_{\mathrm{s}}^{+} \sin \left(\omega_{1} t+\theta^{+}\right) \\ u_{\mathrm{s} \alpha}^{-}=U_{\mathrm{s}}^{-} \cos \left(\omega_{1} t+\theta^{-}\right) \\ u_{\mathrm{s} \beta}^{-}=-U_{\mathrm{s}}^{-} \sin \left(\omega_{1} t+\theta^{-}\right) \end{array}\right. $ | (22) |
对式(22)求导可得
| $ \left\{\begin{array}{l} \frac{\mathrm{d} u_{\mathrm{s} \alpha}^{+}}{\mathrm{d} t}=-\omega_{1} U_{\mathrm{s}}^{+} \sin \left(\omega_{1} t+\theta^{+}\right)=-\omega_{1} u_{\mathrm{s} \beta}^{+} \\ \frac{\mathrm{d} u_{\mathrm{s} \beta}^{+}}{\mathrm{d} t}=-\omega_{1} U_{\mathrm{s}}^{+} \cos \left(\omega_{1} t+\theta^{+}\right)=\omega_{1} u_{\mathrm{s} \alpha}^{+} \\ \frac{\mathrm{d} u_{\mathrm{s} \alpha}^{-}}{\mathrm{d} t}=-\omega_{1} U_{\mathrm{s}}^{-} \sin \left(\omega_{1} t+\theta^{-}\right)=\omega_{1} u_{\mathrm{s} \beta}^{-} \\ \frac{\mathrm{d} u_{\mathrm{s} \beta}^{-}}{\mathrm{d} t}=-\omega_{1} U_{\mathrm{s}}^{-} \cos \left(\omega_{1} t+\theta^{-}\right)=-\omega_{1} u_{\mathrm{s} \alpha}^{-} \end{array}\right. $ | (23) |
进一步可以得到
| $ \frac{\mathrm{d} \boldsymbol{u}_{\mathrm{s}}}{\mathrm{d} t}=\left[\begin{array}{c} -\omega_{1} u_{\mathrm{s} \beta} \\ \omega_{1} u_{\mathrm{s} \alpha} \end{array}\right] $ | (24) |
根据上述分析, 式(20)可写为
| $\frac{\mathrm{d} \boldsymbol{x}}{\mathrm{d} t}=\boldsymbol{A} \boldsymbol{x}+\boldsymbol{B} \boldsymbol{u}+\boldsymbol{F}$ | (25) |
其中,
| $ \boldsymbol{A}=\left[\begin{array}{cc}-\frac{R_{0}}{L_{0}} & -\omega_{1} \\ \omega_{1} & -\frac{R_{0}}{L_{0}}\end{array}\right], \quad \boldsymbol{B}=\left[\begin{array}{cc}\frac{3 u_{\mathrm{s} \alpha}}{2 L_{0}} & \frac{3 u_{\mathrm{s} \beta}}{2 L_{0}} \\ \frac{3 u_{\mathrm{s} \beta}}{2 L_{0}} & -\frac{3 u_{\mathrm{s} \alpha}}{2 L_{0}}\end{array}\right] \\ \boldsymbol{x}=\left[\begin{array}{l}P \\ Q\end{array}\right], \quad \boldsymbol{F}=\left[\begin{array}{c}\frac{-1.5 u_{\mathrm{s}}^{2}}{L_{0}} \\ 0\end{array}\right]$ |
根据滑模理论, 选择有功偏差和无功偏差为零作为滑模面, 即
| $ \left\{\begin{array}{l} S_{P}=P_{\mathrm{ref}}-P=\frac{\mathrm{d} P}{\mathrm{d} t}=0 \\ S_{Q}=Q_{\mathrm{ref}}-Q=\frac{\mathrm{d} Q}{\mathrm{d} t}=0 \end{array}\right. $ | (26) |
将式(20)代入式(26), 可得
| $\frac{\mathrm{d} \boldsymbol{S}}{\mathrm{d} \boldsymbol{t}}=-\boldsymbol{Ax}-\boldsymbol{Bu}-\boldsymbol{F}$ | (27) |
本文采用指数趋近律, 并且为了消除在滑模面切换过程中产生的抖动, 采用饱和函数代替符号函数。这样, 可得输出的交流侧参考电压为
| $\left[\begin{array}{c}v_{\alpha} \\ v_{\beta}\end{array}\right]= \\ -\boldsymbol{B}^{-1}\left[\begin{array}{c}\boldsymbol{A}_{1} \boldsymbol{X}_{1}+F_{1}+K_{11} S_{P}+K_{12} \operatorname{sat}\left(S_{P}\right) \\ \boldsymbol{A}_{2} \boldsymbol{X}_{2}+F_{2}+K_{21} S_{Q}+K_{22} \operatorname{sat}\left(S_{Q}\right)\end{array}\right]$ | (28) |
式中:K11, K12, K21, K22——调节系数;
sat(SP), sat(SQ)——SP, SQ的饱和函数。
饱和函数定义为
| $ \operatorname{sat}\left(S_{i}\right)=\left\{\begin{array}{ll} 1 & S \geqslant \Delta_{i} \\ \frac{S_{i}}{\lambda_{i}} & \left|S_{i}\right| \leqslant \Delta_{i} \\ -1 & S_{i} \leqslant-\Delta_{i} \end{array}\right. $ | (29) |
式中:Δi——边界层;
i=P, Q。
上面控制策略的稳定性和收敛性可由Lyapunov稳定性判据得以判定。可以构造Lyapunov函数为
| $ V=\boldsymbol{SS}^{\mathrm{T}}=S_{P}^{2}+S_{Q}^{2} $ | (30) |
由式(28)可知, V≥0恒成立。
| $\begin{aligned} \frac{\mathrm{d} \boldsymbol{S} \boldsymbol{S}^{T}}{\mathrm{d} t}=& 2 S_{P} \frac{\mathrm{d} S_{P}}{\mathrm{d} t}+2 S_{Q} \frac{\mathrm{d} S_{Q}}{\mathrm{d} t}=\\ &-2\left[K_{11} S_{P}+K_{12} \operatorname{sat}\left(S_{P}\right)+\right.\\ &\left.K_{21} S_{Q}+K_{22} \operatorname{sat}\left(S_{Q}\right)\right] \end{aligned}$ | (31) |
选取的Lyapunov函数随时间的增加而减小, 直至收缩到零, 即系统可以收敛于换切面。由初始值SP0和SQ0到达滑模面的时间为
| $\left\{\begin{array}{l}T_{P}=\frac{\ln \left(\frac{S_{P 0}+K_{12}}{K_{11}}\right)-\ln \frac{K_{12}}{K_{11}}}{K_{11}} \\ T_{Q}=\frac{\ln \left(\frac{S_{Q 0}+K_{22}}{K_{21}}\right)-\ln \frac{K_{22}}{K_{21}}}{K_{21}}\end{array}\right.$ | (32) |
由式(32)可知, 系统可在一定时间内收敛至滑动面, 且通过减小K11和K21或增大K12和K22加快趋近过程。
2.4 PBC控制策略的设计
2.4.1 不平衡电网电压下MMC的EL模型
将式(1)转换到两相旋转坐标系下并整理为
| $\frac{\mathrm{d}}{\mathrm{d} t}\left[\begin{array}{c}i_{\mathrm{s} d}^{+} \\ i_{\mathrm{s}q}^{+}\end{array}\right]=-\left[\begin{array}{cc}\frac{R_{0}}{L_{0}} & -\omega \\ \omega & \frac{R_{0}}{L_{0}}\end{array}\right]\left[\begin{array}{c}i_{\mathrm{s} d}^{+} \\ i_{\mathrm{s} q}^{+}\end{array}\right]+\frac{1}{L_{0}}\left[\begin{array}{c}u_{\mathrm{s} d}^{+}-u_{d}^{+} \\ u_{\mathrm{s} q}^{+}-u_{q}^{+}\end{array}\right]$ | (33) |
| $\frac{\mathrm{d}}{\mathrm{d} t}\left[\begin{array}{c}i_{\mathrm{s}d}^{-} \\ i_{\mathrm{s}q}^{-}\end{array}\right]=-\left[\begin{array}{cc}\frac{R_{0}}{L_{0}} & \omega \\ -\omega & \frac{R_{0}}{L_{0}}\end{array}\right]\left[\begin{array}{c}i_{\mathrm{s}d}^{-} \\ i_{\mathrm{s}q}^{-}\end{array}\right]+\frac{1}{L_{0}}\left[\begin{array}{c}u_{\mathrm{s}d}^{-}-u_{d}^{-} \\ u_{\mathrm{s}q}^{-}-u_{q}^{-}\end{array}\right]$ | (34) |
将式(33)和式(34)写成EL模型为
| $ \left\{\begin{array}{l} \boldsymbol{M} \dot{\boldsymbol{x}}^{+}+\boldsymbol{J}^{+} \boldsymbol{x}^{+}+\boldsymbol{R} \boldsymbol{x}^{+}=\boldsymbol{u}^{+} \\ \boldsymbol{M} \dot{\boldsymbol{x}}^{-}+\boldsymbol{J}^{-} \boldsymbol{x}^{-}+\boldsymbol{R} \boldsymbol{x}^{-}=\boldsymbol{u}^{-} \end{array}\right. $ | (35) |
其中,
| $ \boldsymbol{M}=\left[\begin{array}{cc} L_{0} & 0 \\ 0 & L_{0} \end{array}\right], \quad \boldsymbol{J}^{+}=\left[\begin{array}{cc} 0 & -\omega L_{0} \\ \omega L_{0} & 0 \end{array}\right] , $ |
| $ \boldsymbol{J}^{-}=\left[\begin{array}{cc} 0 & \omega L_{0} \\ -\omega L_{0} & 0 \end{array}\right], \quad \boldsymbol{R}=\left[\begin{array}{cc} R_{0} & 0 \\ 0 & R_{0} \end{array}\right] , $ |
| $ \boldsymbol{u}^{+}=\left[\begin{array}{c} u_{\mathrm{s} d}^{+}-u_{d}^{+} \\ u_{\mathrm{sq}}^{+}-u_{q}^{+} \end{array}\right], \quad \boldsymbol{u}^{-}=\left[\begin{array}{c} u_{\mathrm{s} d}^{-}-u_{d}^{-} \\ u_{\mathrm{s} q}^{-}-u_{q}^{-} \end{array}\right] , $ |
| $ \boldsymbol{x}^{+}=\left[\begin{array}{c} i_{d}^{+} \\ i_{q}^{+} \end{array}\right], \quad \boldsymbol{x}^{-}=\left[\begin{array}{l} i_{d}^{-} \\ i_{q}^{+} \end{array}\right] $ |
式中:M——正定的对角阵;
J+, J-——正、负系统的反对称矩阵;
R——对称正定矩阵, 能够反映系统的能量耗散特性;
x+, x-——正、负系统的状态变量;
u+, u-——正、负系统的输入。
2.4.2 MMC的无源性及稳定性
考虑m输入m输出系统
| $\left\{\begin{array}{l}\dot{\boldsymbol{x}}=\boldsymbol{f}(\boldsymbol{x, u}) \\ \boldsymbol{y}=\boldsymbol{h}(\boldsymbol{x})\end{array}\right.$ | (36) |
式中:x——状态量, x∈Rn;
u——输入, u∈Rm;
y——输出, y∈Rm;
m, n——输入输出和状态量的维数;
f(x, u)——关于(x, u)的局部Lipschitz函数。
对于式(36), 如果存在连续可为半正定能量存储函数H(x)(能量存储函数)及正定函数Q(x), 对于∀t > 0使得耗散不等式
| $H(\boldsymbol{x}(t))-H(\boldsymbol{x}(0)) \leqslant \\ \int_{0}^{t} \boldsymbol{y} \boldsymbol{u}^{\mathrm{T}} \mathrm{d} \tau-\int_{0}^{t} Q(\boldsymbol{x}) \mathrm{d} \tau$ | (37) |
或
| $\dot{H}(\boldsymbol{x}) \leqslant \boldsymbol{y} \boldsymbol{u}^{\mathrm{T}}-Q(\boldsymbol{x})$ | (38) |
对系统的输入u、输出y及能量供给率yuT成立, 则系统是严格无源的。
本文选择正、负序无源系统的能量存储函数分别为
| $ \left\{\begin{array}{l} V^{+}=\frac{\boldsymbol{x}^{+\mathrm{T}} \boldsymbol{M} \boldsymbol{x}^{+}}{2} \\ V^{-}=\frac{\boldsymbol{x}^{-\mathrm{T}} \boldsymbol{M} \boldsymbol{x}^{-}}{2} \end{array}\right. $ | (39) |
进而可得
| $ \left\{\begin{aligned} \dot{V}^{+}=\boldsymbol{x}^{+\mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{x}}^{+} & =x^{+\mathrm{T}}\left(\boldsymbol{u}^{+}-\boldsymbol{J}^{+} \boldsymbol{x}^{+}\right.\\ \left.-\boldsymbol{R} \boldsymbol{x}^{+}\right) & =\boldsymbol{x}^{+\mathrm{T}} \boldsymbol{u}-\boldsymbol{x}^{+\mathrm{T}} \boldsymbol{R} \boldsymbol{x}^{+\mathrm{T}} \\ \dot{V}^{-}=\boldsymbol{x}^{-\mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{x}}^{-} & =x^{-\mathrm{T}}\left(\boldsymbol{u}^{-}-\boldsymbol{J}^{-} \boldsymbol{x}^{-}\right.\\ \left.-\boldsymbol{R} \boldsymbol{x}^{-}\right) & =\boldsymbol{x}^{-\mathrm{T}} \boldsymbol{u}-\boldsymbol{x}^{-\mathrm{T}} \boldsymbol{R} \boldsymbol{x}^{-\mathrm{T}} \end{aligned}\right. $ | (40) |
分别令y=x+、Q(x)=x+TRx+和y=x-、Q(x)=x-TRx-, 则式(40)可以化为式(37)的形式, 说明不平衡电网电压下的MMC系统为严格无源的。根据无源控制理论, 严格无源的系统必定可以采用无源控制策略且控制系统稳定。
2.4.3 MMC正负序PBC控制器的设计
对两相旋转坐标系下正负两个PBC控制器进行设计, 需要确定期望的稳定平衡点。当电网电压发生不平衡时, 期望的稳定平衡点为
| $\boldsymbol{x}^{+*}=\left[\begin{array}{l}i_{d\text{ref}}^{+} \\ i_{q\text{ref}}^{+}\end{array}\right], \boldsymbol{x} x^{-*}=\left[\begin{array}{l}i_{d\text{ref}}^{-} \\ i_{q\text{ref }}^{-}\end{array}\right]$ | (41) |
式中:
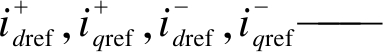 正、负序系统中状态变量
正、负序系统中状态变量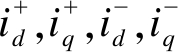 的参考值。
的参考值。
令正、负序系统的状态变量的误差分别为
| $ \left\{\begin{array}{l} \boldsymbol{x}_{\mathrm{e}}^{+}=\boldsymbol{x}^{+}-\boldsymbol{x}^{+} \\ \boldsymbol{x}_{\mathrm{e}}^{-}=\boldsymbol{x}^{-}-\boldsymbol{x}^{-} \end{array}\right. $ | (42) |
则可以得到
| $ \left\{\begin{aligned} \boldsymbol{M x}_{\mathrm{e}}^{+}+\boldsymbol{J} \boldsymbol{x}_{\mathrm{e}}^{+}+\boldsymbol{R} \boldsymbol{x}_{\mathrm{e}}^{+} & =\boldsymbol{u}^{+}-\boldsymbol{M} \boldsymbol{x}^{+} \\ -\boldsymbol{J} \boldsymbol{x}^{+*} & -\boldsymbol{R} \boldsymbol{x}^{+*} \\ \boldsymbol{M} \boldsymbol{x}_{\mathrm{e}}^{-}+\boldsymbol{J} \boldsymbol{x}_{\mathrm{e}}^{-}+\boldsymbol{R} \boldsymbol{x}_{\mathrm{e}}^{-} & =\boldsymbol{u}^{-}-\boldsymbol{M} \boldsymbol{x}^{-}-\\ \boldsymbol{J}^{-} \boldsymbol{x}^{-*} & -\boldsymbol{R} \boldsymbol{x}^{-*} \end{aligned}\right. $ | (43) |
正、负序系统的误差能量函数取为
| $ \left\{\begin{array}{l} H^{+}=\frac{\boldsymbol{x}_{\mathrm{e}}^{+\mathrm{T}} \boldsymbol{M x}_{\mathrm{e}}^{+}}{2} \\ H^{-}=\frac{\boldsymbol{x}_{\mathrm{e}}^{-\mathrm{T}}\boldsymbol{M x} _{\mathrm{e}}^{-}}{2} \end{array}\right. $ | (44) |
只要使H+和H-收敛到零, 则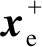 和
和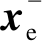 也能收敛到零, 即可达到PBC控制的目的。为了使系统快速收敛到所希望的点, 误差能量函数迅速变为零, 需要注入阻尼来加速系统的能量耗散, 从而加快系统的响应速度[8]。注入阻尼耗散项为
也能收敛到零, 即可达到PBC控制的目的。为了使系统快速收敛到所希望的点, 误差能量函数迅速变为零, 需要注入阻尼来加速系统的能量耗散, 从而加快系统的响应速度[8]。注入阻尼耗散项为
| $ \left\{\begin{array}{l} \boldsymbol{R}_{d}^{+} \boldsymbol{x}_{\mathrm{e}}^{+}=\left(\boldsymbol{R}_{0}+\boldsymbol{R}_{\mathrm{a}}^{+}\right) \boldsymbol{x}_{\mathrm{e}}^{+} \\ \boldsymbol{R}_{d}^{-} \boldsymbol{x}_{\mathrm{e}}^{-}=\left(\boldsymbol{R}_{0}-\boldsymbol{R}_{\mathrm{a}}^{-}\right) \boldsymbol{x}_{\mathrm{e}} \end{array}\right. $ | (45) |
其中,
| $ \boldsymbol{R}_{\mathrm{a}}^{+}=\left[\begin{array}{cc} R_{\mathrm{a} 1}^{+} & 0 \\ 0 & R_{\mathrm{a} 2}^{+} \end{array}\right], \quad \boldsymbol{R}_{\mathrm{a}}^{-}=\left[\begin{array}{cc} R_{\mathrm{a} 1}^{-} & 0 \\ 0 & R_{\mathrm{a} 2}^{-} \end{array}\right] $ |
式中:
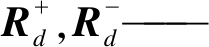 正、负序系统注入的阻尼正定矩阵。
正、负序系统注入的阻尼正定矩阵。
结合式(45)可将式(43)改写为
| $ \left\{\begin{aligned} \boldsymbol{M} \boldsymbol{x}_{\mathrm{e}}^{+}+\boldsymbol{R}_{d}^{+} \boldsymbol{x}_{\mathrm{e}}^{+}=\boldsymbol{u}^{+}-\left[\boldsymbol{M} \boldsymbol{x}^{+*}\right.& +\\ \boldsymbol{J}^{+}\left(\boldsymbol{x}^{+*}+\boldsymbol{x}_{\mathrm{e}}^{+}\right)+\boldsymbol{R} \boldsymbol{x}^{+*} & -\boldsymbol{R}_{\mathrm{a}}^{+} \boldsymbol{x}_{\mathrm{e}}^{+} \\ \boldsymbol{M} \boldsymbol{x}_{\mathrm{e}}^{-}+\boldsymbol{R}_{d}^{-} \boldsymbol{x}_{\mathrm{e}}^{-}=\boldsymbol{u}^{-}-\left[\boldsymbol{M} \boldsymbol{x}^{-*}+\right.\\ \boldsymbol{J}^{-}\left(\boldsymbol{x}^{-*}+\boldsymbol{x}_{\mathrm{e}}^{-}\right)+\boldsymbol{R} \boldsymbol{x}^{-*} & -\boldsymbol{R}_{\mathrm{a}}^{-} \boldsymbol{x}_{\mathrm{e}}^{+} \end{aligned}\right. $ | (46) |
进而可以推出正、负序系统的PBC控制器的控制信号分别为:
| $ \left\{\begin{array}{l} u_{d}^{+}=u_{\mathrm{s} d}^{+}+\omega L_{0} i_{q}^{+}-R_{0} i_{d\text{ref}}^{+}+R_{\mathrm{a}1}^{+}\left(i_{d}^{+}-i_{d\text{ref}}^{+}\right) \\ u_{q}^{+}=u_{\mathrm{s} q}^{+}-\omega L_{0} i_{q}^{+}-R_{0} i_{q\text{ref }}^{+}+R_{\mathrm{a} 2}^{+}\left(i_{q}^{+}-i_{q\text{ref }}^{+}\right) \end{array}\right. $ | (47) |
| $ \left\{\begin{array}{l} u_{d}^{-}=u_{\mathrm{s} d}^{-}+\omega L_{0} i_{q}^{-}-R_{0} i_{d\text{ref}}^{-}+R_{\mathrm{a} 1}^{-}\left(i_{d}^{-}-i_{d\text{ref}}^{-}\right) \\ u_{q}^{-}=u_{\mathrm{s} q}^{-}-\omega L_{0} i_{q}^{-}-R_{0} i_{q\text{ref }}^{-}+R_{\mathrm{a} 2}^{-}\left(i_{q}^{-}-i_{q\text{ref }}^{-}\right) \end{array}\right. $ | (48) |
3 仿真结果及分析
3.1 控制目标1下的仿真
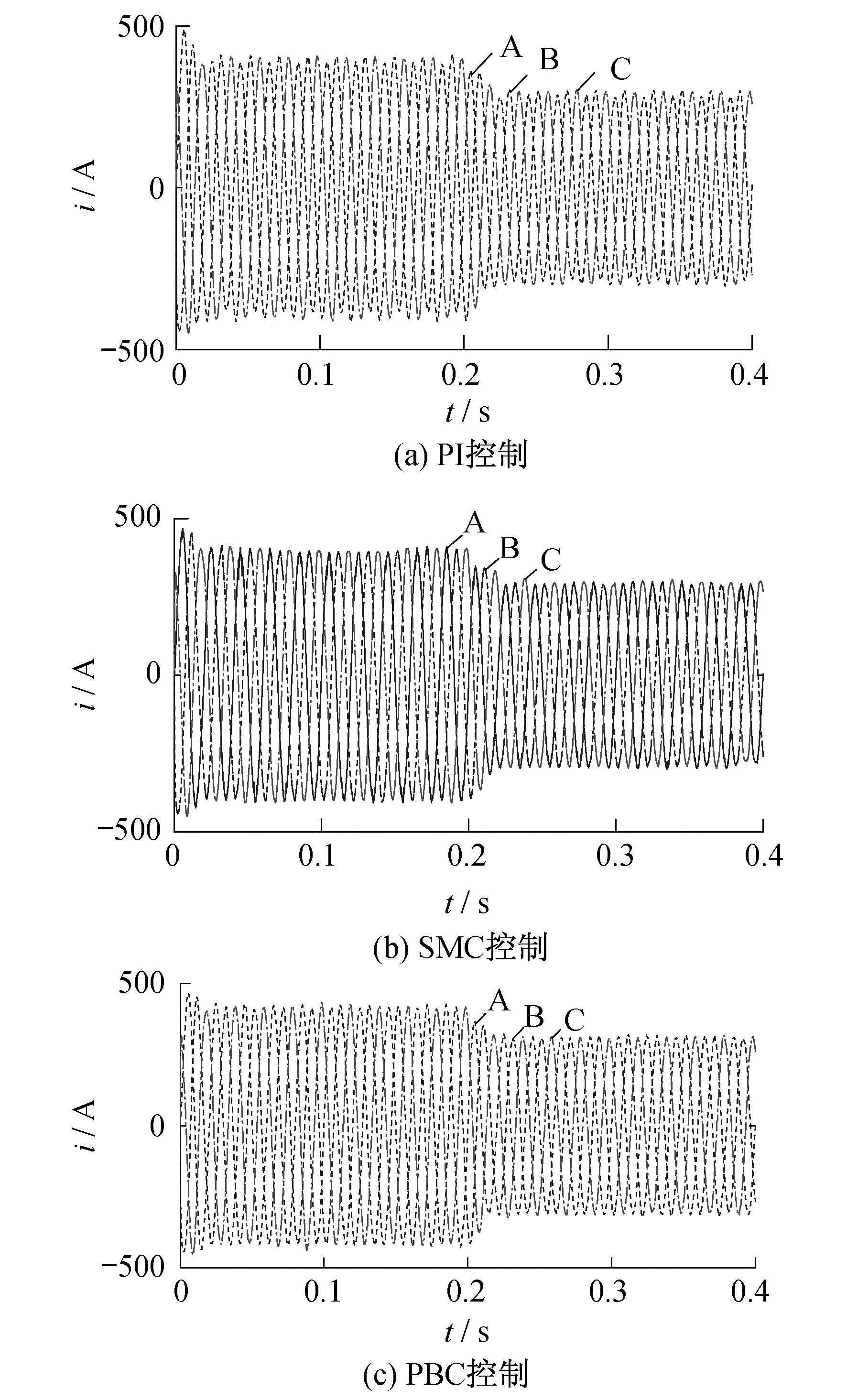
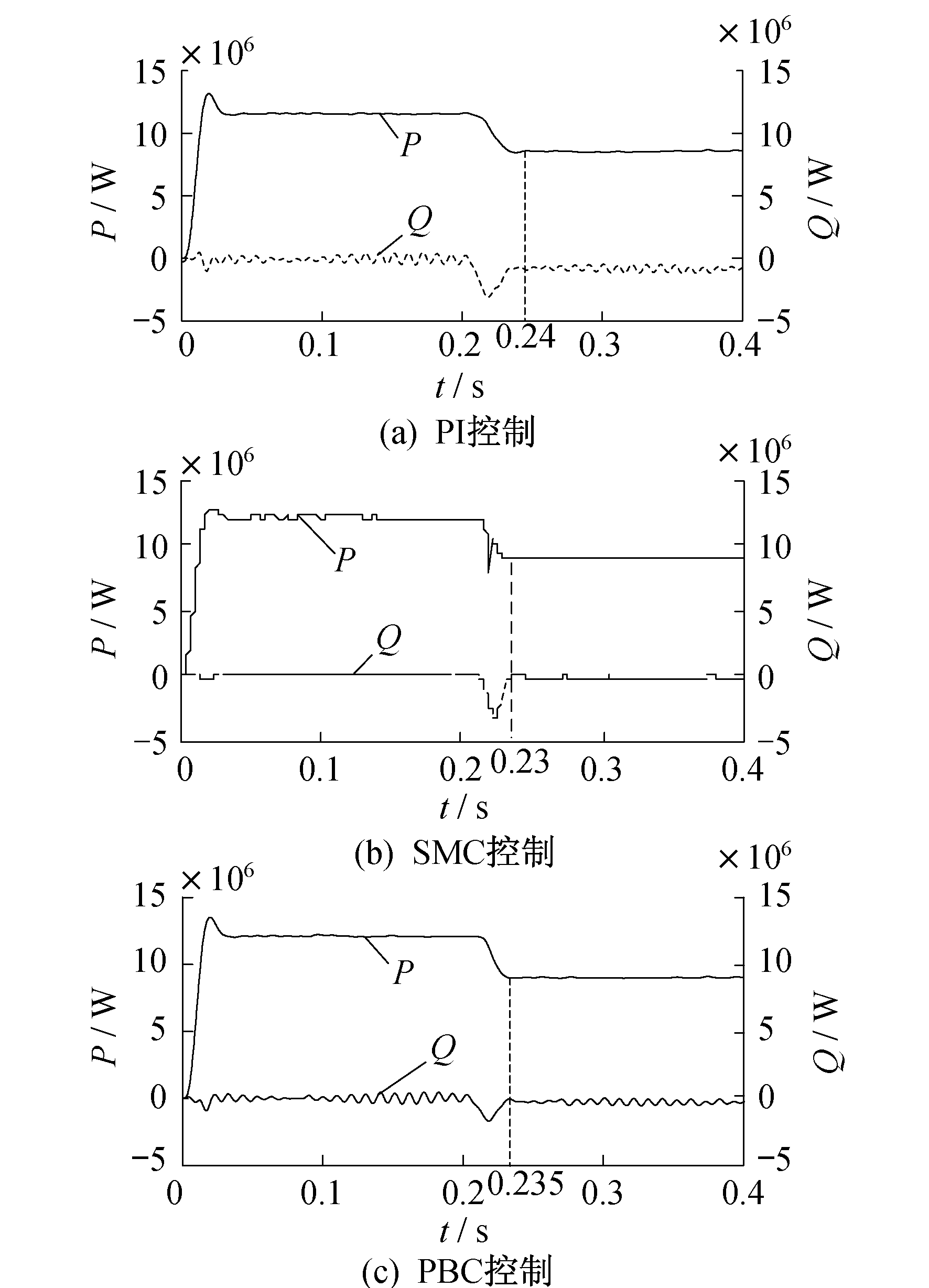
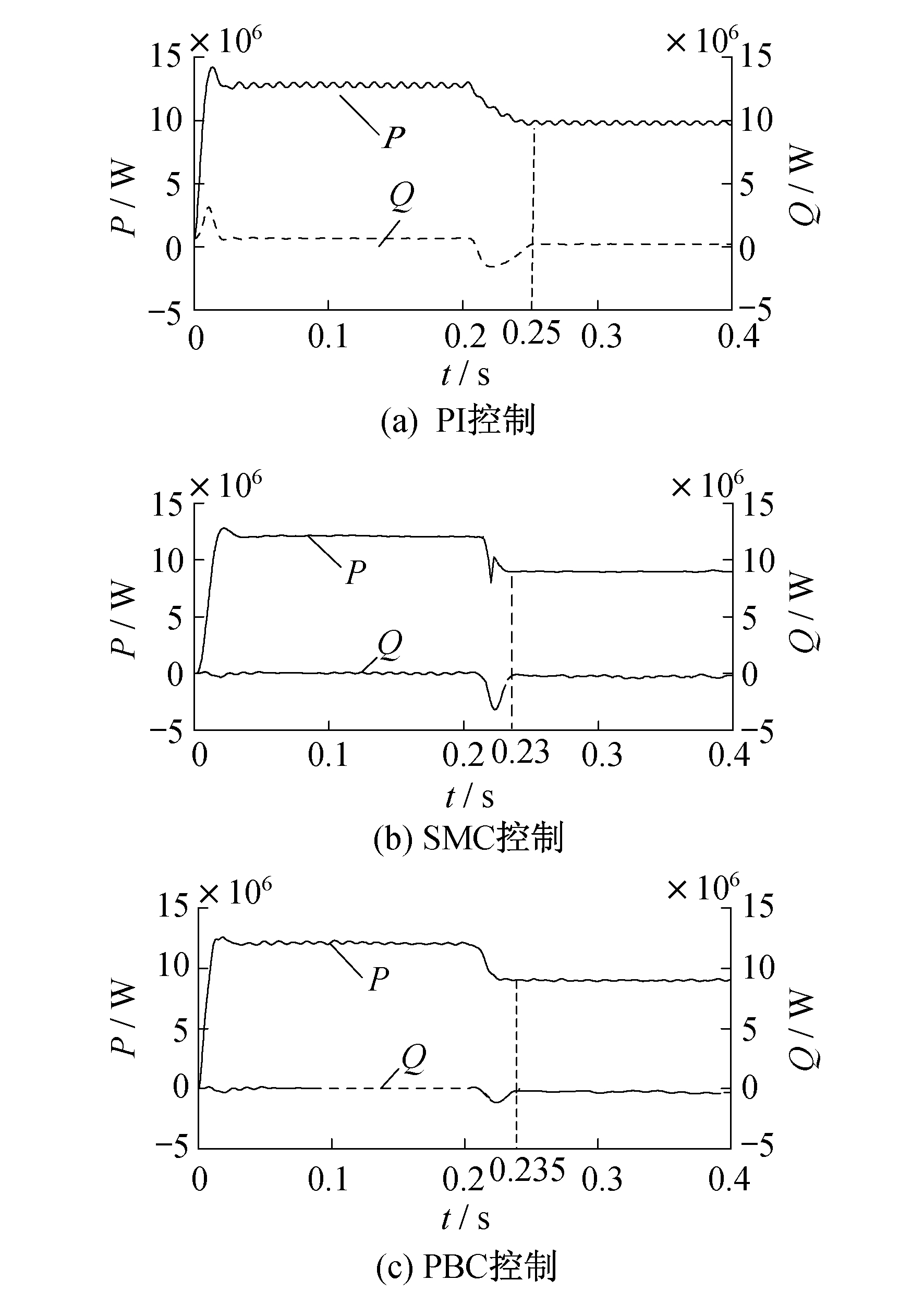
控制目标1(交流侧电流为三相对称交流电)下3种控制策略的交流侧电流波形和功率波形分别如图 1和图 2所示。
通过图 1和图 2可以看出:3种控制策略法对于控制目标1的实现都可以达到理想的结果, 即交流侧的三相电流基本保持三相对称, 但此时有功功率和无功功率都会产生脉动; 就谐波含量而言, 传统PI控制和SMC控制的谐波含量比基于能量原理的PBC控制高; 在三相给定的功率发生变化时, 传统PI控制反应速度较慢, 大约比其他2种方法慢10 ms。为了进一步比较3种控制策略下的三相电流的对称程度, 引入了电流不平衡系数(Current Unbalanced Factor, CUF)这一概念, 3种方法下的CUF如表 2所示。
表 2
控制目标1下3种控制策略的CUF %
| 控制策略 | CUF |
| PI控制 | 3.5 |
| SMC控制 | 2.7 |
| PBC控制 | 1.8 |
通过表 2可知, 传统PI控制的电流不对称度最高, 其次为SMC控制, 而PBC控制可以达到2%以下, 效果最好。
3.2 控制目标2下的仿真
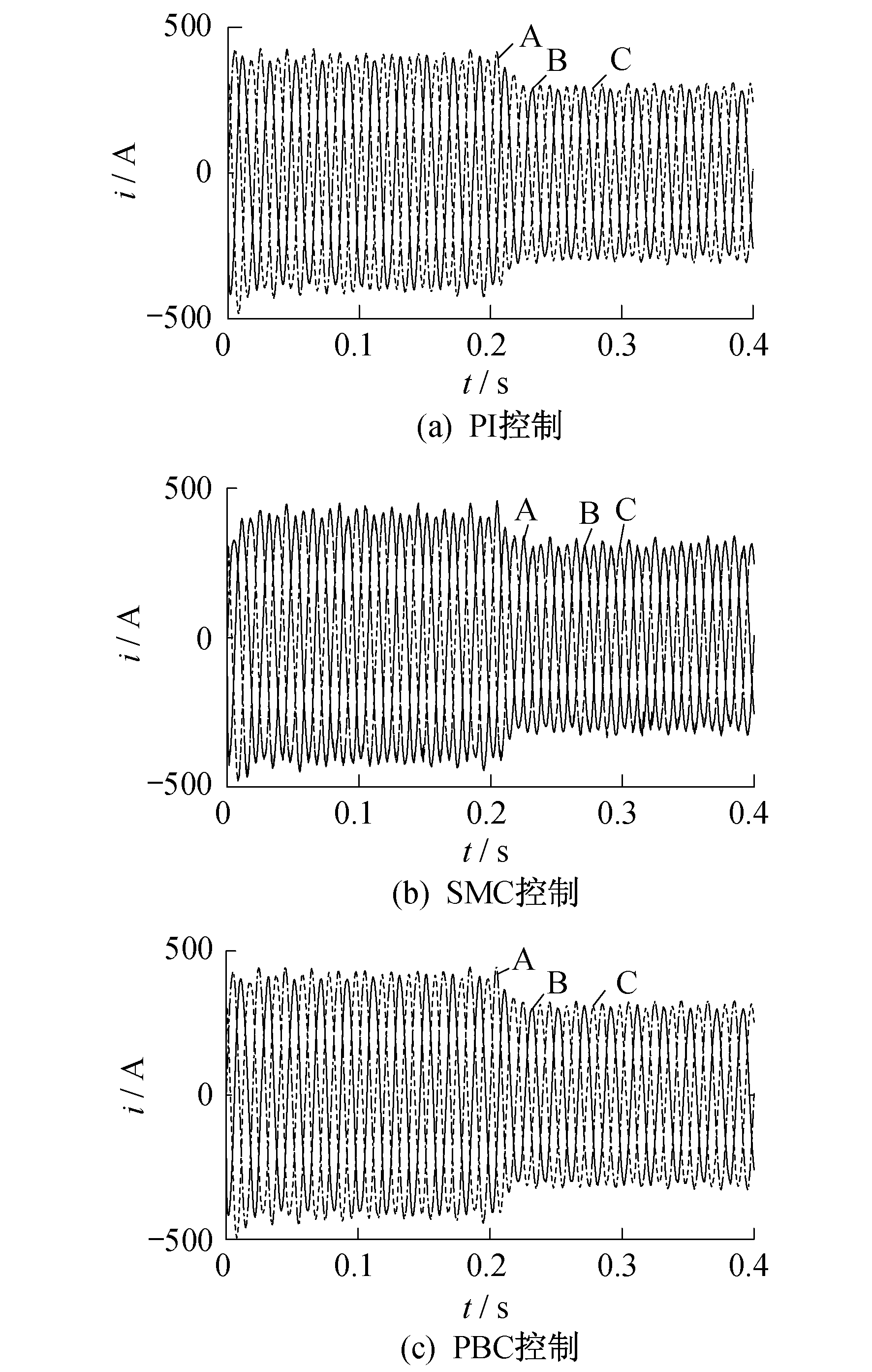
控制目标2(有功功率无脉动)下3种控制策略的交流侧电流波形和功率波形分别如图 3和图 4所示。
通过图 3和图 4可知:3种控制策略基本都可实现控制目标2, 但此时电流不再对称, 无功功率也会出现二次脉动; 传统的PI控制的超调量较高, 在给定功率发生改变时, 使用PI控制经过0.4 s后达到稳定, 使用PBC控制需要0.35 s, 而使用SMC控制仅需要0.3 s。为了进一步比较各种控制策略中有功功率谐波的含量, 测试了3种控制策略下有功功率的总谐波畸变率(Total Harmonic Distortion, THD)。其中, PI控制下有功功率的THD为6.15%, SMC控制下有功功率的THD为6.50%, 而PBC控制下有功功率的THD最小, 为2.45%。
3.3 控制目标3下的仿真
4 结语
本文针对电网电压不平衡产生的问题, 分别采用传统PI控制、SMC控制、PBC控制3种不同控制策略。通过理论推导和软件仿真表明, 后2种的控制效果都优于传统PI控制, 其中PBC控制的电流不平衡度和谐波含量都小于其他两种方法, SMC控制的响应速度最快。
参考文献
-
[1]国内外配电前沿技术动态及发展[J]. 中国电机工程学报, 2016, 36(6): 1552-1567.
-
[2]MAYA J, XAVIER D P. Smart grid development in Quebec: A review and policy approach[J]. Renewable and Sustainable Energy Reviews, 2018, 82(2): 1922-1930.
-
[3]YANG F, ZHANG D Z, SUN C W. China's regional balanced development based on the investment in power grid infrastructure[J]. Renewable and Sustainable Energy Reviews, 2016, 53(1): 1549-1557.
-
[4]SUN W S, CHENG Q M, CHENG Y M, et al. A new control strategy for MMC under grid voltage unbalance condition[J]. International Transactions on Electrical Energy Systems, 2019, 29(5): 1-16.
-
[5]不平衡及谐波电网下并网逆变器的谐振滑模控制技术[J]. 中国电机工程学报, 2014, 34(9): 1345-1352.
-
[6]广义谐波电网环境电压源型并网变流器滑模变结构直接功率控制策略[J]. 电网技术, 2016, 40(6): 1845-1850.
-
[7]电压不平衡下双馈感应发电机机侧变换器PBC控制方法[J]. 电力系统自动化, 2016, 40(19): 73-81. DOI:10.7500/AEPS20150915004
-
[8]基于PCHD模型的光伏Z源并网逆变器PBC控制[J]. 高电压技术, 2016, 42(9): 2723-2732.
-
[9]电网不平衡下DFIG网侧变换器侧基于PCHD模型的PBC控制[J]. 电网技术, 2017, 41(5): 1627-1635.
-
[10]基于准Z源逆变器的光伏发电系统的双滑模变结构控制[J]. 上海电力学院学报, 2017, 33(5): 459-465.