|
|
|
发布时间: 2019-12-10 |
|
|
|
|
收稿日期: 2019-06-14
基金项目: 国家自然科学基金(61873159);上海市科学技术委员会项目(18020500700)
中图法分类号: TM76
文献标识码: A
文章编号: 1006-4729(2019)06-0580-07
|
摘要
为了提高传统风能最大功率点跟踪控制的鲁棒性, 提出了新的滑模自适应最大功率点跟踪控制策略。由于实际无速度传感器的风电系统变量难以测量, 为此构造了滑模状态观测器来估计系统的转速跟踪误差, 并基于估计值设计了滑模自适应最大功率点跟踪控制器。最后, 基于MATLAB/Simulink仿真平台搭建了完整的风电系统仿真模型。仿真结果表明, 在不同风速扰动作用下, 所提出的控制策略均能实现良好的跟踪和控制效果, 提高了风电系统的鲁棒性, 保证了风电系统的最大功率输出。
关键词
风电系统; 状态观测器; 最大功率点跟踪; 滑模自适应控制
Abstract
A new Maximum Power Point Tracking control strategy based on sliding mode adaptive control is put forward to improve the robustness of traditional MPPT control in the wind power system.As the variable is difficult to measure in the wind power system without speed sensor, the sliding mode state observer is designed.The observer is used to estimate the rotating speed error and the sliding mode adaptive controller is constructed based on the observer value.In the end, the simulation model is built based on the MATLAB/Simulink platform.The simulation results show that the proposed control strategy can achieve good tracking and control effect under the different wind speed disturbance, improve the robustness of wind power system and ensure the maximum power output of wind power system.
Key words
wind power system; state observer; max power point tracking; sliding mode adaptive control
随着能源危机和环境污染的日趋严重, 风力发电作为目前最有商业开发潜力的新能源发电技术受到了广泛研究和推广[1]。与双馈感应电机相比, 永磁同步电机(Permanent Magnet Synchronous Generator, PMSG)具有结构简单、效率高、控制灵活等优点[2-3], 因此基于永磁同步电机的变速风力发电系统是未来发展的方向。
最大功率点跟踪(Maximum Power Point Tracking, MPPT)是风机在额定风速以下的主要运行策略, 目前已有很多相关研究成果。文献[4]对风力发电系统最大功率点跟踪进行了研究, 基于RT-LAB实时仿真平台搭建了2.5 MW直驱式永磁风力发电系统仿真模型, 对不同风速条件下, 直驱式永磁风力发电系统的工作情况进行了实时仿真实验。文献[5]建立了小信号系统模型, 利用梯度估计法设计了转矩补偿器来补偿传统最优电磁转矩的给定值, 可以减小较大转动惯量对风机转速的影响; 但是, 梯度估计法的方向最优只是局部性质, 对于整体而言不能保证寻求的是最优补偿, 不能完全保证系统运行在最优点。文献[6]提出了一种智能控制算法, 通过检测风速变化, 采用模糊推理估测最佳风机转速, 同时结合神经网络算法对隶属度函数的输入和输出进行了调整; 但是, 该文献只对最优转速进行了优化, 跟踪控制仍采用传统的最优电磁转矩法。文献[7]采用基于增强学习法的神经网络控制, 通过定时检测风速的变化来调整最大运行点, 数据实时更新, 可靠性较高; 但这种实时跟踪调整方案的经济性较差, 且不能保证风速检测的精度。文献[8]采用磁链和转矩观测器对磁链和转矩进行了观测, 省去了复杂的坐标变换、繁琐计算等环节; 但是, 转速偏差控制采用PID算法, 对干扰的抑制作用较弱。文献[9]提出了基于扩张状态观测器的滑模控制; 但鲁棒性较差, 同时扩张状态增加了系统方程的阶数, 更加难以控制。
根据以上分析, 本文提出了基于滑模状态观测器的最大功率点跟踪控制策略。相比于其他控制方式, 基于观测器的滑模控制结构相对简单, 且节约系统成本, 同时可实现对干扰的动态补偿。利用MATLAB/Simulink仿真平台搭建系统模型, 通过不同算例来验证所设计的滑模自适应最大功率点跟踪控制器的优越性。
1 永磁直驱风电系统结构
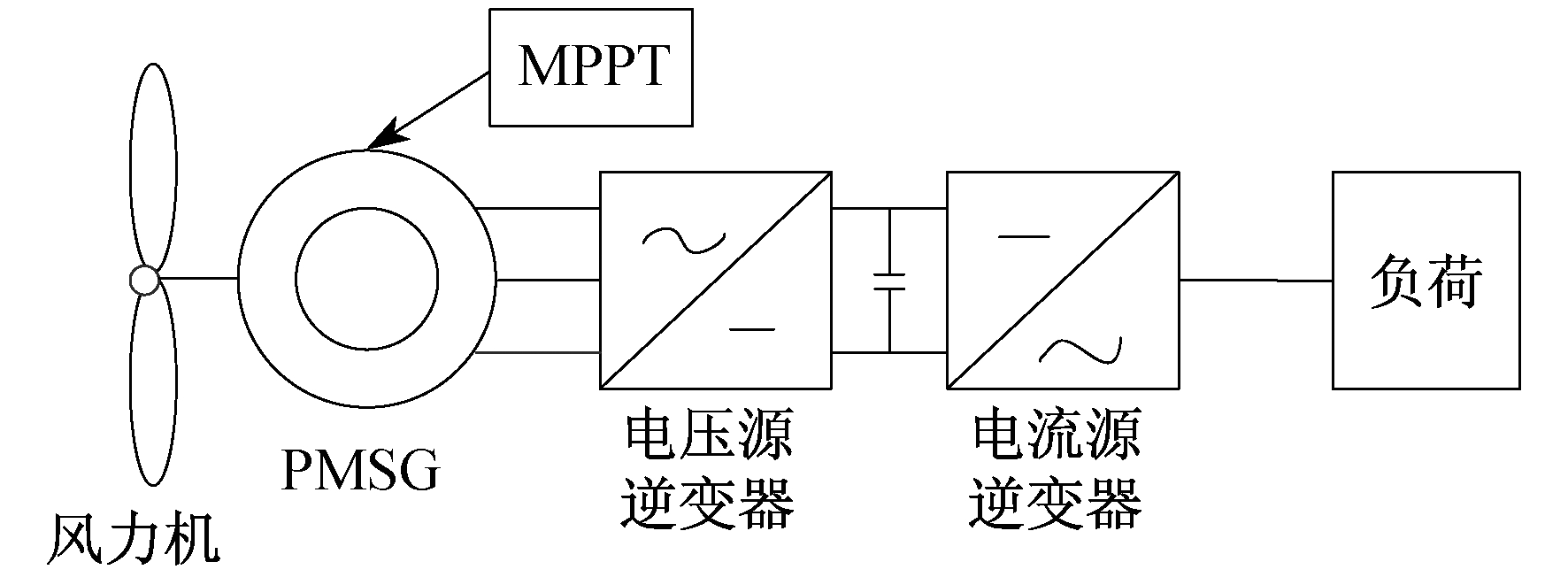
本文采用的是永磁直驱风电系统, 主要包括风力机, PMSG, 变流环节, 负荷。其结构如图 1所示。
风电系统的控制分为低于额定风速的最大功率点跟踪控制和高于额定风速的变速变桨控制。本文主要研究低于额定风速的最大功率点跟踪控制, 以保证最大限度地利用风能。
1.1 风机的机械特性
根据空气动力学原理, 风机从自然随机变化的风中所能捕获的机械功率Pw[10]为
| $ P_{\mathrm{w}}=\frac{1}{2} \pi \rho R^{2} v_{\mathrm{w}}^{3} C_{\mathrm{P}}(\lambda, \beta) $ | (1) |
| $ \lambda=\frac{w_{\mathrm{w}}}{R} $ | (2) |
| $ \mathrm{C}_{\mathrm{p}}=0.517\;6\left(\frac{116}{\tau}-0.4 \beta-5\right) \mathrm{e}^{\frac{-21}{\tau}}+0.006\;8 \lambda $ | (3) |
| $ \tau=\frac{1}{\frac{1}{\lambda+0.08 \beta}-\frac{0.035}{\beta^{3}+1}} $ | (4) |
式中:ρ——空气密度;
R——风机的叶片半径;
vw——风速;
Cp——风机的风能利用系数;
λ——叶尖速比;
β——桨距角;
ww——风机的叶轮转速。
1.2 永磁同步电机的数学模型
在dq旋转坐标系下, 永磁同步电机一般采用以下模型[11-15]
| $ \left\{\begin{array}{l} u_{d}=R_{\mathrm{a}} i_{d}-w_{\mathrm{e}} L_{q} i_{q}+L_{d} \frac{\mathrm{d} i_{d}}{\mathrm{d} t} \\ u_{q}=R_{\mathrm{a}} i_{q}+w_{\mathrm{e}} L_{d} i_{d}+w_{\mathrm{e}} \varphi_{\mathrm{a}}+L_{q} \frac{\mathrm{d} i_{q}}{\mathrm{d} t} \end{array}\right. $ | (5) |
式中:ud, uq, id, iq, Ld, Lq——d轴和q轴上的电压、电流、电感;
we——磁链旋转的电角速度;
Ra——定子电阻;
φa——永磁转子的磁链。
电磁转矩方程[10]为
| $ T_{\mathrm{e}}=\frac{3}{2} p \varphi_{\mathrm{a}} i_{q} $ | (6) |
式中:Te——电磁转矩;
p——极对数。
直驱永磁同步风电系统的运动方程为
| $ T_{\mathrm{L}}-T_{\mathrm{e}}-B_{\mathrm{m}} w_{\mathrm{g}}=J_{\mathrm{eq}} \frac{\mathrm{d} w_{\mathrm{g}}}{\mathrm{d} t} $ | (7) |
式中:TL——负载转矩;
Bm——黏性摩擦因数;
wg——电机的机械角速度;
Jeq——等效转动惯量。
由于永磁直驱风机系统省略了齿轮箱, 通过传动轴直接连接, 所以风机的转速等于电机的转速, 即ww=wg。
1.3 变流器数学模型
变流环节采用的是背靠背式双PWM结构, 包括机侧PWM整流器、直流环节和网侧PWM逆变器。三相静止坐标系模型经abc/dq(派克变换)转换为两相旋转坐标系模型[13]。
机侧整流器的数学模型为
| $ \left\{\begin{aligned} L_{\mathrm{f}} \frac{\mathrm{d} i_{\mathrm{m}_{-} d}}{\mathrm{d} t}=& -R_{\mathrm{f}} i_{\mathrm{m}_{-} d}+\omega_{\mathrm{e}} L_{\mathrm{f}} i_{\mathrm{m}_{-} q}+\\ & E_{\mathrm{m}_{-} d}-S_{\mathrm{m}_{-} d} U_{\mathrm{dc}} \\ L_{\mathrm{f}} \frac{\mathrm{d} i_{\mathrm{m}_{-} q}}{\mathrm{d} t}=& -R_{\mathrm{f}} i_{\mathrm{m}_{-} q}-\omega_{\mathrm{e}} L_{\mathrm{f}} i_{\mathrm{m}_{-} d}+\\ & E_{\mathrm{m}_{-} q}-S_{\mathrm{m}_{q}} U_{\mathrm{dc}} \end{aligned}\right. $ | (8) |
网侧逆变器的数学模型为
| $ \left\{\begin{array}{c} L_{\mathrm{f}} \frac{\mathrm{d} i_{\mathrm{g}_{-} d}}{\mathrm{d} t}=-R_{\mathrm{f}} i_{\mathrm{g}_{-} d}+\omega_{\mathrm{g}} L_{\mathrm{f}} i_{\mathrm{g}_{-} q}+ \\ U_{\mathrm{g}_{-} d}-S_{\mathrm{g}_{-} d} U_{\mathrm{dc}} \\ L_{\mathrm{f}} \frac{\mathrm{d} i_{\mathrm{g}_{-} q}}{\mathrm{d} t}=-R_{\mathrm{f}} i_{\mathrm{g}_{-} q}-\omega_{\mathrm{g}} L_{\mathrm{f}} i_{\mathrm{g}_{-} d}+ \\ U_{\mathrm{g}_{-} q}-S_{\mathrm{g}_{-} q} U_{\mathrm{dc}} \end{array}\right. $ | (9) |
直流环节部分可以表示为
| $ C \frac{\mathrm{d} U_{\mathrm{dc}}}{\mathrm{d} t}=\frac{3}{2} S_{\mathrm{m}_{-} d} i_{\mathrm{m}_{-} d}+\frac{3}{2} S_{\mathrm{m}_{-} q} i_{\mathrm{m}_{-} q}-i_{\mathrm{L}} $ | (10) |
式中:Lf, Rf——滤波电路的电感和电阻;
im_d, im_q——三相交流电流的d轴和q轴分量;
Em_d, Em_q——三相交流电源电压的d轴和q轴分量;
Sm_d, Sm_q——机侧整流器的d轴和q轴开关函数;
Udc——直流环节的电压值;
ig_d, ig_q——电网电流的d轴和q轴分量;
Ug_d, Ug_q——电网电压的d轴和q轴分量;
Sg_d, Sg_q——网侧逆变器的d轴和q轴开关函数;
iL——流入网侧逆变器的电流。
2 直驱式永磁同步风电系统的MPPT控制
最大功率点跟踪控制的目的是为了提高风能利用率。传统的最优电磁转矩法将风机转矩等同于电机电磁转矩, 忽略了风电传动轴的损耗。本文将风电转轴损耗量考虑在内, 结合传动轴方程和电磁转矩方程得
| $ \dot{w}_{\mathrm{g}}=\frac{1}{J} T_{\mathrm{w}}\left(w_{\mathrm{g}}, v_{\mathrm{w}}\right)-\frac{1.5 p \varphi_{\mathrm{a}}}{J} i_{q}-\frac{B_{\mathrm{m}}}{J} w_{\mathrm{g}} $ | (11) |
为便于书写, 记变化量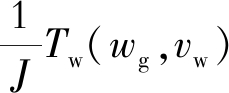 为
为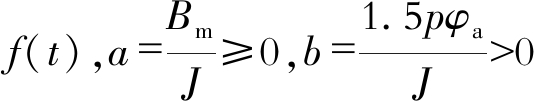 为常数, 则式(11)转化为
为常数, 则式(11)转化为
| $ \dot{w}_{\mathrm{g}}=-a w_{\mathrm{g}}-b i_{q}+f(t) $ | (12) |
取状态变量x=wref-wg, 控制变量u=iq, 得
| $ \begin{aligned} \dot{\boldsymbol{x}}=& -\dot{w}_{\mathrm{g}}=a w_{\mathrm{g}}+b i_{q}-f(t)=\\ & a\left(w_{\mathrm{ref}}-\boldsymbol{x}\right)+b i_{q}-f(t)=\\ & -a \boldsymbol{x}+b \boldsymbol{u}-f(t)+d \\ d=& a w_{\mathrm{ref}} \end{aligned} $ |
系统的状态方程为
| $\begin{aligned} \dot{\boldsymbol{x}}(t)=\boldsymbol{A} \boldsymbol{x}(t) &+\boldsymbol{B u}(t)+\boldsymbol{\Gamma} \boldsymbol{\xi}(t) \\ \boldsymbol{y}(t) &=\boldsymbol{C} \boldsymbol{x}(t) \end{aligned}$ | (13) |
式中:Γ——具有适当维数的常数矩阵;
ξ——系统干扰。
2.1 滑模观测器的设计
滑模观测器能有效估计不确定电力系统的状态变量, 故基于式(13), 设计滑模观测器[16]满足
| $ \begin{aligned} \mathit{\boldsymbol{\dot {\hat x}}}(t)=\boldsymbol{A} \hat{\boldsymbol{x}}(t)+\boldsymbol{B u}(t) & +\boldsymbol{L}(\boldsymbol{y}(t)-\\ \hat{\boldsymbol{y}}(t))+\boldsymbol{\Lambda} v \hat{\boldsymbol{y}}(t) & =\boldsymbol{C} \hat{\boldsymbol{x}}(t) \end{aligned} $ | (14) |
式中:L——观测器增益矩阵;
 观测器增益矩阵;
观测器增益矩阵;
v——补偿控制;
Λ——系数矩阵, 矩阵CΛ是列满秩的, (A, Λ)可控。
由式(13)和式(14)可得到误差系统为
| $ \left\{\begin{aligned} \dot{\boldsymbol{e}}=& (\boldsymbol{A}-\boldsymbol{L} \boldsymbol{C}) \boldsymbol{e}+\boldsymbol{\Gamma} \boldsymbol{\xi}-\boldsymbol{\Lambda} v=\\ & \boldsymbol{A}_{\mathrm{c}} \boldsymbol{e}+\boldsymbol{\Gamma} \boldsymbol{\xi}-\boldsymbol{\Lambda} v \\ e_{y}=& \boldsymbol{C} \boldsymbol{e} \end{aligned}\right. $ | (15) |
其中,
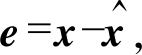 理想滑模满足
理想滑模满足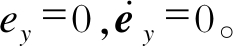
将式(14)代入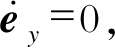 得到等价控制
得到等价控制
| $v_{\mathrm{eq}}=(\boldsymbol{C} \boldsymbol{\Lambda})^{-1} \boldsymbol{C}(\boldsymbol{A} \boldsymbol{e}+\boldsymbol{\Gamma} \boldsymbol{\xi})$ | (16) |
由式(15)和式(16)可得误差系统理想滑模的状态方程为
| $ \begin{aligned} {\mathit{\boldsymbol{\dot e}}}=& \left[\boldsymbol{I}-\boldsymbol{\Lambda}(\boldsymbol{C} \boldsymbol{\Lambda})^{-1} \boldsymbol{C}\right] \boldsymbol{A} \boldsymbol{e}+\\ & \left[\boldsymbol{I}-\boldsymbol{\Lambda}(\boldsymbol{C} \boldsymbol{\Lambda})^{-1} \boldsymbol{C}\right] \boldsymbol{\Gamma} \boldsymbol{\xi} \end{aligned} $ | (17) |
矩阵[I-Λ(CΛ)-1C]A具有m个零特征值和n-m个指定特征值, 所以理想滑动模态是渐进稳定的。
由于证明的需要, 给出以下假设。
假设1 系统干扰满足‖ξ‖≤M, M为已知正数。
假设2 假设存在m×m矩阵D使得
| $\boldsymbol{\Gamma}=\boldsymbol{\Lambda} \boldsymbol{D}$ | (18) |
给出以下定理1, 可以使误差系统方程式(15)渐进稳定。
定理1 选择正定矩阵P满足(A-LC)TP+P(A-LC)+PTInP < 0, 构造补偿控制器满足
| $ v\mathit{\boldsymbol{ = w}}\frac{{\mathit{\boldsymbol{Ce}}}}{{\left\| {\mathit{\boldsymbol{Ce}}} \right\|}} $ | (19) |
并且
| $ \lambda_{\min }(\boldsymbol{w}) \geqslant M\|\boldsymbol{D}\| \frac{\lambda_{\max } \boldsymbol{C} \boldsymbol{P}^{-1} \boldsymbol{C}^{\mathrm{T}}}{\lambda_{\min } \boldsymbol{C P}^{-1} \boldsymbol{C}^{\mathrm{T}}} $ | (20) |
和
| $\boldsymbol{\Lambda}=\boldsymbol{P}^{-1} \boldsymbol{C}^{\mathrm{T}} \boldsymbol{w}^{-1}$ | (21) |
式中:w——m×m矩阵。
那么, 误差系统方程式(15)是渐进稳定的。
证 明 对系统构造李雅普诺夫函数
| $V(t)=\boldsymbol{e}^{\mathrm{T}} \boldsymbol{Pe} $ | (22) |
当Ce=0时, v=veq得
| $ \begin{array}{l} \dot{V}=\boldsymbol{e}^{\mathrm{T}}\left(\boldsymbol{A}_{\mathrm{c}}^{\mathrm{T}} \boldsymbol{P}+\boldsymbol{P} \boldsymbol{A}_{\mathrm{c}}\right) \boldsymbol{e}+2 \boldsymbol{e}^{\mathrm{T}} \boldsymbol{C}^{\mathrm{T}} \boldsymbol{w}^{-1} \boldsymbol{D} \boldsymbol{\xi}- \\ 2 \boldsymbol{e}^{\mathrm{T}} \boldsymbol{C}^{\mathrm{T}} \boldsymbol{w}^{-1} v_{\mathrm{eq}}=\boldsymbol{e}^{\mathrm{T}}\left(\boldsymbol{A}_{\mathrm{c}}^{\mathrm{T}} \boldsymbol{P}+\boldsymbol{P} \boldsymbol{A}_{\mathrm{c}}\right) \boldsymbol{e}+ \\ \boldsymbol{e}^{\mathrm{T}}\left(\boldsymbol{A}_{\mathrm{c}}^{\mathrm{T}} \boldsymbol{P}+\boldsymbol{P} \boldsymbol{A}_{\mathrm{c}}\right) \boldsymbol{e}\left(\boldsymbol{D} \boldsymbol{\xi}-v_{\mathrm{eq}}\right)=\boldsymbol{e}^{\mathrm{T}}\left(\boldsymbol{A}_{\mathrm{c}}^{\mathrm{T}} \boldsymbol{P}+\right. \\ \left.\left.\boldsymbol{P} \boldsymbol{A}_{\mathrm{c}}\right) \boldsymbol{e}+\boldsymbol{e}^{\mathrm{T}}\left(\boldsymbol{A}_{\mathrm{c}}^{\mathrm{T}} \boldsymbol{P}+\boldsymbol{P} \boldsymbol{A}_{\mathrm{c}}\right) \boldsymbol{e}\left[\boldsymbol{D} \boldsymbol{\xi}-(\boldsymbol{C} \boldsymbol{\Lambda})^{-1} \boldsymbol{C} \boldsymbol{\Gamma} \boldsymbol{\xi}\right)\right]= \\ \boldsymbol{e}^{\mathrm{T}}\left(\boldsymbol{A}_{\mathrm{c}}^{\mathrm{T}} \boldsymbol{P}+\boldsymbol{P} \boldsymbol{A}_{\mathrm{c}}\right) \boldsymbol{e}+\boldsymbol{e}^{\mathrm{T}}\left(\boldsymbol{A}_{\mathrm{c}}^{\mathrm{T}} \boldsymbol{P}+\boldsymbol{P} \boldsymbol{A}_{\mathrm{c}}\right) \boldsymbol{e}[\boldsymbol{D} \boldsymbol{\xi}- \\ \left.\left.(\boldsymbol{C} \boldsymbol{\Lambda})^{-1} \boldsymbol{C} \boldsymbol{\Lambda} \boldsymbol{D} \boldsymbol{\xi}\right)\right]=\boldsymbol{e}^{\mathrm{T}}\left(\boldsymbol{A}_{\mathrm{c}}^{\mathrm{T}} \boldsymbol{P}+\boldsymbol{P} \boldsymbol{A}_{\mathrm{c}}\right) \boldsymbol{e} \lt 0 \end{array} $ |
当Ce≠0时,
| $ \begin{array}{l} \dot{V}=\dot{\boldsymbol{e}}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{e}+\boldsymbol{e}^{\mathrm{T}} \boldsymbol{P} \dot{\boldsymbol{e}}=\boldsymbol{e}^{\mathrm{T}}\left(\boldsymbol{A}_{\mathrm{c}}^{\mathrm{T}} \boldsymbol{P}+\boldsymbol{P} \boldsymbol{A}_{\mathrm{c}}\right) \boldsymbol{e}+ \\ (\boldsymbol{\Gamma} \boldsymbol{\xi}-\boldsymbol{\Lambda} \boldsymbol{v})^{\mathrm{T}} \boldsymbol{P} \boldsymbol{e}+\boldsymbol{e}^{\mathrm{T}} P(\boldsymbol{\Gamma} \boldsymbol{\xi}-\boldsymbol{\Lambda} \boldsymbol{v})= \\ \boldsymbol{e}^{\mathrm{T}}\left(\boldsymbol{A}_{\mathrm{c}}^{\mathrm{T}} \boldsymbol{P}+\boldsymbol{P} \boldsymbol{A}_{\mathrm{c}}\right) \boldsymbol{e}+2 \boldsymbol{e}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{\Gamma} \boldsymbol{\xi}- \\ 2 \boldsymbol{e}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{\Lambda} v=\boldsymbol{e}^{\mathrm{T}}\left(\boldsymbol{A}_{\mathrm{c}}^{\mathrm{T}} \boldsymbol{P}+\boldsymbol{P} \boldsymbol{A}_{\mathrm{c}}\right) \boldsymbol{e}+ \\ 2 \boldsymbol{e}^{\mathrm{T}} \boldsymbol{C}^{\mathrm{T}}\left(\boldsymbol{w}^{-1} \boldsymbol{D} \boldsymbol{\xi}-\frac{\boldsymbol{C} \boldsymbol{e}}{\|\boldsymbol{C} \boldsymbol{e}\|}\right) \leqslant \\ \boldsymbol{e}^{\mathrm{T}}\left(\boldsymbol{A}_{\mathrm{c}}^{\mathrm{T}} \boldsymbol{P}+\boldsymbol{P} \boldsymbol{A}_{\mathrm{c}}\right) \boldsymbol{e}+ \\ 2\left\|\boldsymbol{e}^{\mathrm{T}} \boldsymbol{C}^{\mathrm{T}}\right\|\left(\left\|\boldsymbol{w}^{-1}\right\|\|\boldsymbol{D}\|\|M\|-1\right) \leqslant \\ \boldsymbol{e}^{\mathrm{T}}\left(\boldsymbol{A}_{\mathrm{c}}^{\mathrm{T}} \boldsymbol{P}+\boldsymbol{P} \boldsymbol{A}_{\mathrm{c}}\right) \boldsymbol{e}+ \\ 2\left\|\boldsymbol{e}^{\mathrm{T}} \boldsymbol{C}^{\mathrm{T}}\right\|\left(\frac{1}{\lambda_{\min }(\boldsymbol{w})}\|\boldsymbol{D}\|\|M\|-1\right) \leqslant \\ \boldsymbol{e}^{\mathrm{T}}\left(\boldsymbol{A}_{\mathrm{c}}^{\mathrm{T}} \boldsymbol{P}+\boldsymbol{P} \boldsymbol{A}_{\mathrm{c}}\right) \boldsymbol{e}+ \\ 2\left\|\boldsymbol{e}^{\mathrm{T}} \boldsymbol{C}^{\mathrm{T}}\right\|\left(\frac{\lambda_{\max } \boldsymbol{C} \boldsymbol{P}^{-1} \boldsymbol{C}^{\mathrm{T}}}{\lambda_{\min } \boldsymbol{C} \boldsymbol{P}^{-1} \boldsymbol{C}^{\mathrm{T}}}-1\right) \leqslant 0 \end{array} $ |
所以, 构造的滑模观测器实现了对未知状态的估计。
2.2 基于滑模观测器的滑模自适应控制器设计
由滑模观测器可观测到系统的状态估计值, 将状态估计值代入到滑模自适应控制器中, 可进一步增强对系统风速变化扰动的控制效果。
2.2.1 切换面的设计
| $s=\boldsymbol{Ex}$ | (23) |
式中:E——具有适当维数的常数矩阵, 选择适当的E使EB非奇异。
当系统进入滑动模态时, s(t)=0, 故有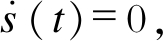 结合式(12)和式(22)可得
结合式(12)和式(22)可得
| $u_{\mathrm{eq}}=-(\boldsymbol{E} \boldsymbol{B})^{-1}(\boldsymbol{E} \boldsymbol{A} \boldsymbol{x}+\boldsymbol{E} \boldsymbol{\Gamma} \boldsymbol{\xi})$ | (24) |
则滑动模态下的系统方程为
| $ \dot{\boldsymbol{x}}=\left[\boldsymbol{A}-\boldsymbol{B}(\boldsymbol{E} \boldsymbol{B})^{-1} \boldsymbol{E} \boldsymbol{A}\right] \boldsymbol{x}-\boldsymbol{B}(\boldsymbol{E} \boldsymbol{B})^{-1} \boldsymbol{E} \boldsymbol{\Gamma} \boldsymbol{\xi} $ | (25) |
令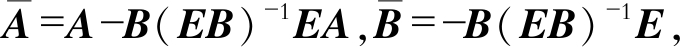 则式(25)可等效为
则式(25)可等效为
| $\boldsymbol{\dot{x}}=\boldsymbol{\bar{A}x}+\boldsymbol{\bar{B} \Gamma \xi}$ | (26) |
构造李雅普诺夫函数
| $V(t)=\boldsymbol{x}^{\mathrm{T}}(t) \boldsymbol{P x}(t)$ | (27) |
| $ \begin{array}{l} \dot{V}=\dot{\boldsymbol{x}}^{\mathrm{T}} \boldsymbol{\bar{P}} \boldsymbol{x}+\boldsymbol{x}^{\mathrm{T}} \overline{\boldsymbol{P}} \dot{\boldsymbol{x}}= \\ (\overline{\boldsymbol{A}} \boldsymbol{x}+\overline{\boldsymbol{B}} \boldsymbol{\Gamma} \boldsymbol{\xi})^{\mathrm{T}} \overline{\boldsymbol{P}} \boldsymbol{x}+\boldsymbol{x}^{\mathrm{T}} \overline{\boldsymbol{P}}(\overline{\boldsymbol{A}} \boldsymbol{x}+\overline{\boldsymbol{B}} \boldsymbol{\Gamma} \boldsymbol{\xi})= \\ \boldsymbol{x}^{\mathrm{T}}\left(\overline{\boldsymbol{A}}^{\mathrm{T}} \overline{\boldsymbol{P}}+\overline{\boldsymbol{P}} \overline{\boldsymbol{A}}\right) \boldsymbol{x}+2\left(\boldsymbol{x}^{\mathrm{T}} \overline{\boldsymbol{P}} \overline{\boldsymbol{B}}+\overline{\boldsymbol{B}} \overline{\boldsymbol{P}} \boldsymbol{x}\right) \boldsymbol{\Gamma} \boldsymbol{\xi}= \\ \boldsymbol{x}^{\mathrm{T}}(-\boldsymbol{Q}) \boldsymbol{x}+2\left(\boldsymbol{x}^{\mathrm{T}} \overline{\boldsymbol{P}} \overline{\boldsymbol{B}}+\overline{\boldsymbol{B}} \overline{\boldsymbol{B}} \boldsymbol{x}\right) \boldsymbol{\Gamma} \boldsymbol{\xi} \leqslant \\ -\lambda_{\min }(\boldsymbol{Q})\|\boldsymbol{x}\|^{2}+ \\ 2\|\boldsymbol{x}\|\|\overline{\boldsymbol{P}}\|\|\overline{\boldsymbol{B}}\| M\|\boldsymbol{\Gamma}\| \end{array} $ |
因此, 当 且λmin(Q) > 0时,
且λmin(Q) > 0时,
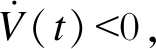 即保证了系统在滑模面s(t)=0上是稳定的。其中, 对于给定的正定对称矩阵
即保证了系统在滑模面s(t)=0上是稳定的。其中, 对于给定的正定对称矩阵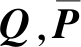 满足
满足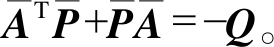
2.2.2 控制器的设计
控制器的趋近律取为
| $\dot{s}=-k s-(\varepsilon+\hat{f}) \operatorname{sgn}(s)$ | (28) |
式中:ε, k——常数, ε > 0, k > 0;
sgn()——符号函数。
自适应律
| $\dot{\hat {f}}=m(\boldsymbol{E B})|s|$ | (29) |
因本文状态方程为一阶, 所以EB为常数。
结合式(24)设计滑模控制器, 满足
| $ \begin{array}{c} u=-(\boldsymbol{E} \boldsymbol{B})^{-1}(\boldsymbol{E} \boldsymbol{A} \hat{x}+\boldsymbol{E} \boldsymbol{M} \boldsymbol{\Gamma})- \\ k s-(\boldsymbol{\varepsilon}+\hat{f}) \operatorname{sgn}(s) \end{array} $ | (30) |
证 明 构造李雅普诺夫函数
| $ V=\frac{1}{2} s^{2}+\frac{1}{2 m} \tilde{f}^{2} $ | (31) |
| $\dot{V}=s \dot{s}+\frac{1}{m} \tilde{f} \dot{\tilde{f}}=s \dot{s}+\frac{1}{m} \tilde{f} \dot{\hat{f}}=$ $s \dot{s}+\frac{1}{m} \tilde{f}(m(\boldsymbol{E} \boldsymbol{B})|s|)= \\ s \boldsymbol{E}\left\{\boldsymbol{A} \boldsymbol{x}+\boldsymbol{B}\left[-(\boldsymbol{E} \boldsymbol{B})^{-1}(\boldsymbol{E} \boldsymbol{A} \hat{\boldsymbol{x}}+\boldsymbol{E} \boldsymbol{M} \boldsymbol{\Gamma})-\right.\right. \\ k s-(\boldsymbol{\varepsilon}+\hat{f}) \operatorname{sgn}(s)]+ \\ \boldsymbol{\Gamma} \boldsymbol{\xi}\}+(\boldsymbol{E} \boldsymbol{B}) \tilde{f}|s|= \\ s\{\boldsymbol{E} \boldsymbol{A}(\boldsymbol{x}-\hat{\boldsymbol{x}})-\boldsymbol{E} \boldsymbol{M} \boldsymbol{\Gamma}-(\boldsymbol{E} \boldsymbol{B})[k s+ \\ (\varepsilon+\hat{f}) \operatorname{sgn}(s)]+\boldsymbol{E} \boldsymbol{\Gamma} \boldsymbol{\xi}\}+(\boldsymbol{E} \boldsymbol{B}) \tilde{f}|s| \leqslant \\ \boldsymbol{E} \boldsymbol{A}(\boldsymbol{x}-\hat{\boldsymbol{x}}) s-(\boldsymbol{E} \boldsymbol{B})[k s+(\varepsilon+\hat{f}) \operatorname{sgn}(s)] s+ \\ (\boldsymbol{E B})(\hat{f}-f)|s| \leqslant\|\boldsymbol{E} \boldsymbol{A}\|\|\boldsymbol{x}-\hat{\boldsymbol{x}}\|\|s\|- \\ \|\boldsymbol{E} \boldsymbol{B}\|\left[k s^{2}+(\boldsymbol{\varepsilon}+\hat{f})|s|\right]+ \\ \|\boldsymbol{E} \boldsymbol{B}\|(\hat{f}-f)|s| \leqslant\|\boldsymbol{E} \boldsymbol{A}\|\|\boldsymbol{x}-\hat{\boldsymbol{x}}\|\|s\|- \\ \|\boldsymbol{E} \boldsymbol{B}\|\left[k s^{2}+(\varepsilon+\hat{f})|s|-(\hat{f}-f)|s|\right] \leqslant \\ \|\boldsymbol{E} \boldsymbol{A}\|\|\boldsymbol{x}-\hat{\boldsymbol{x}}\|\|s\|- \\ \|\boldsymbol{E} \boldsymbol{B}\|\left[k s^{2}+(\varepsilon+f)|s|\right]<0$ |
即系统满足到达条件, 所设计的控制器能够使系统的运动轨迹保持在滑动模态附近。
3 仿真结果分析
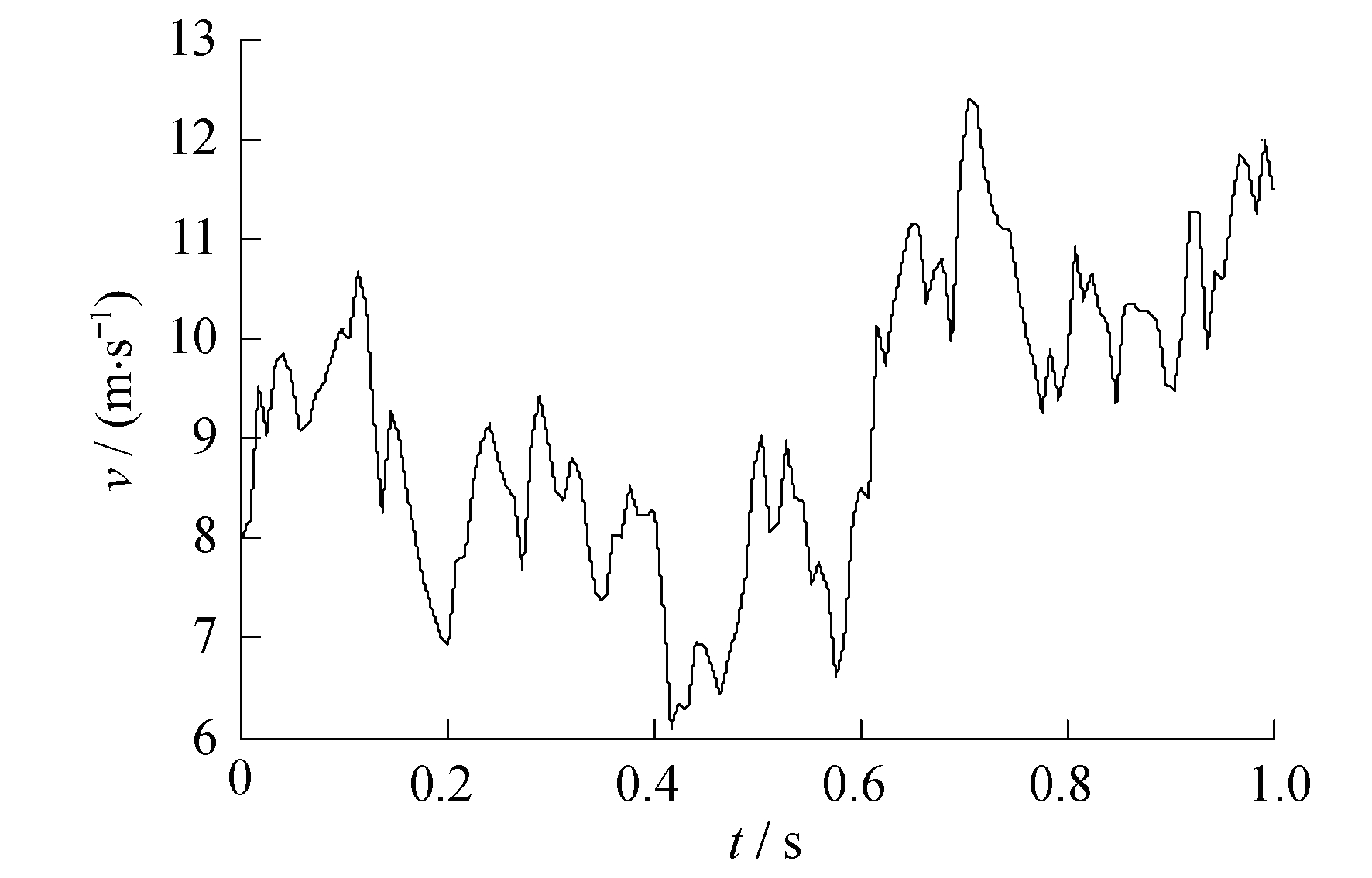
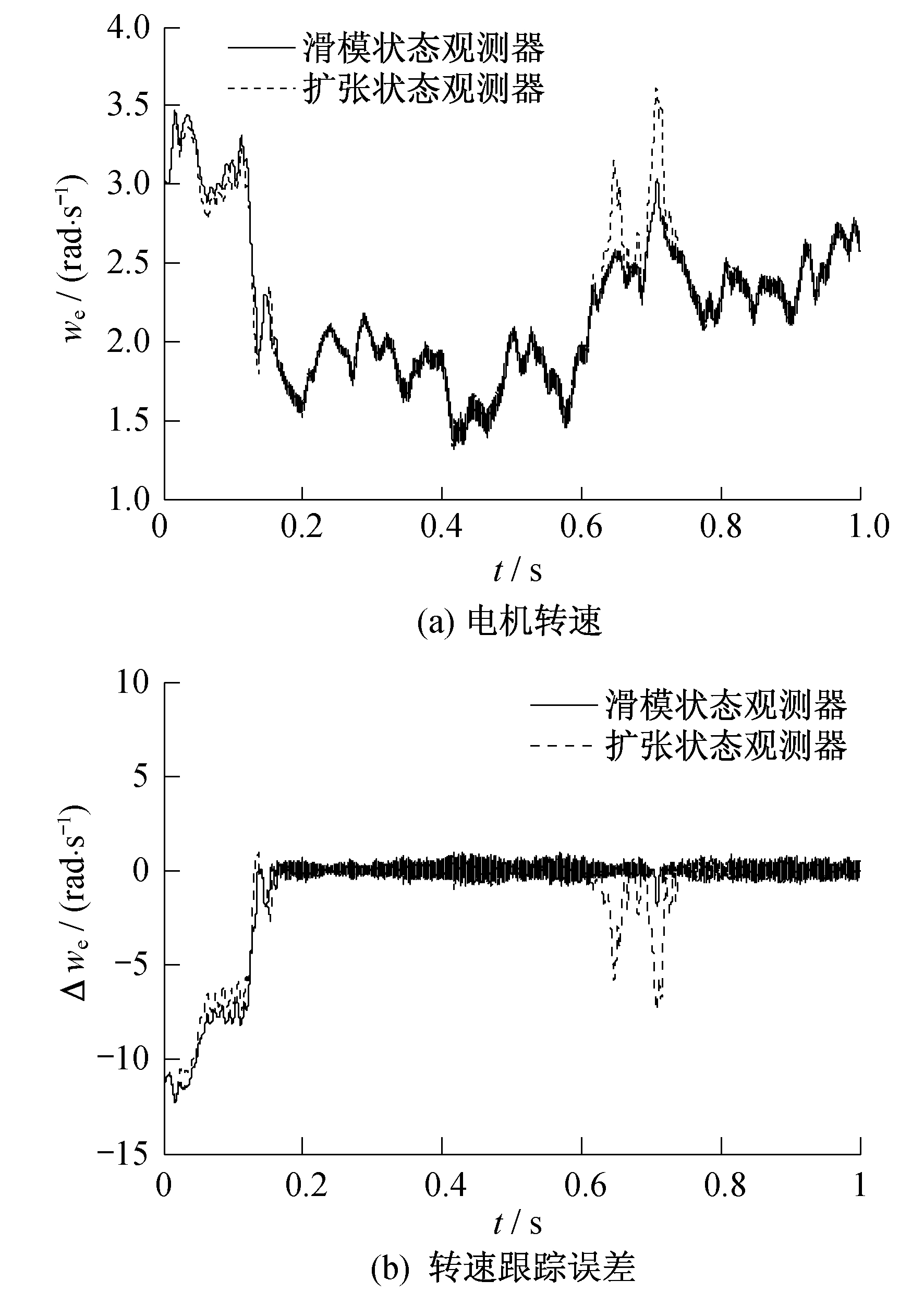
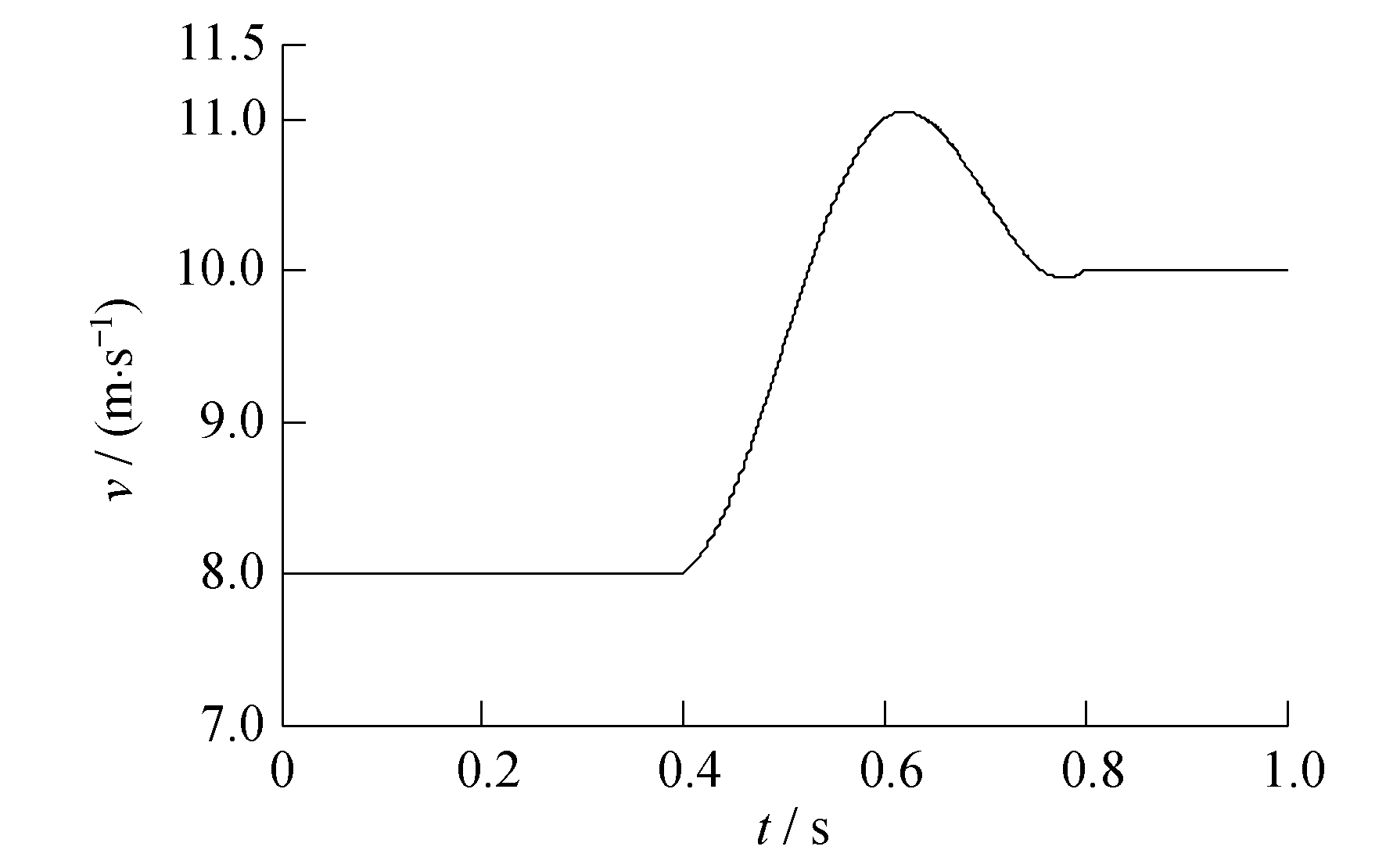
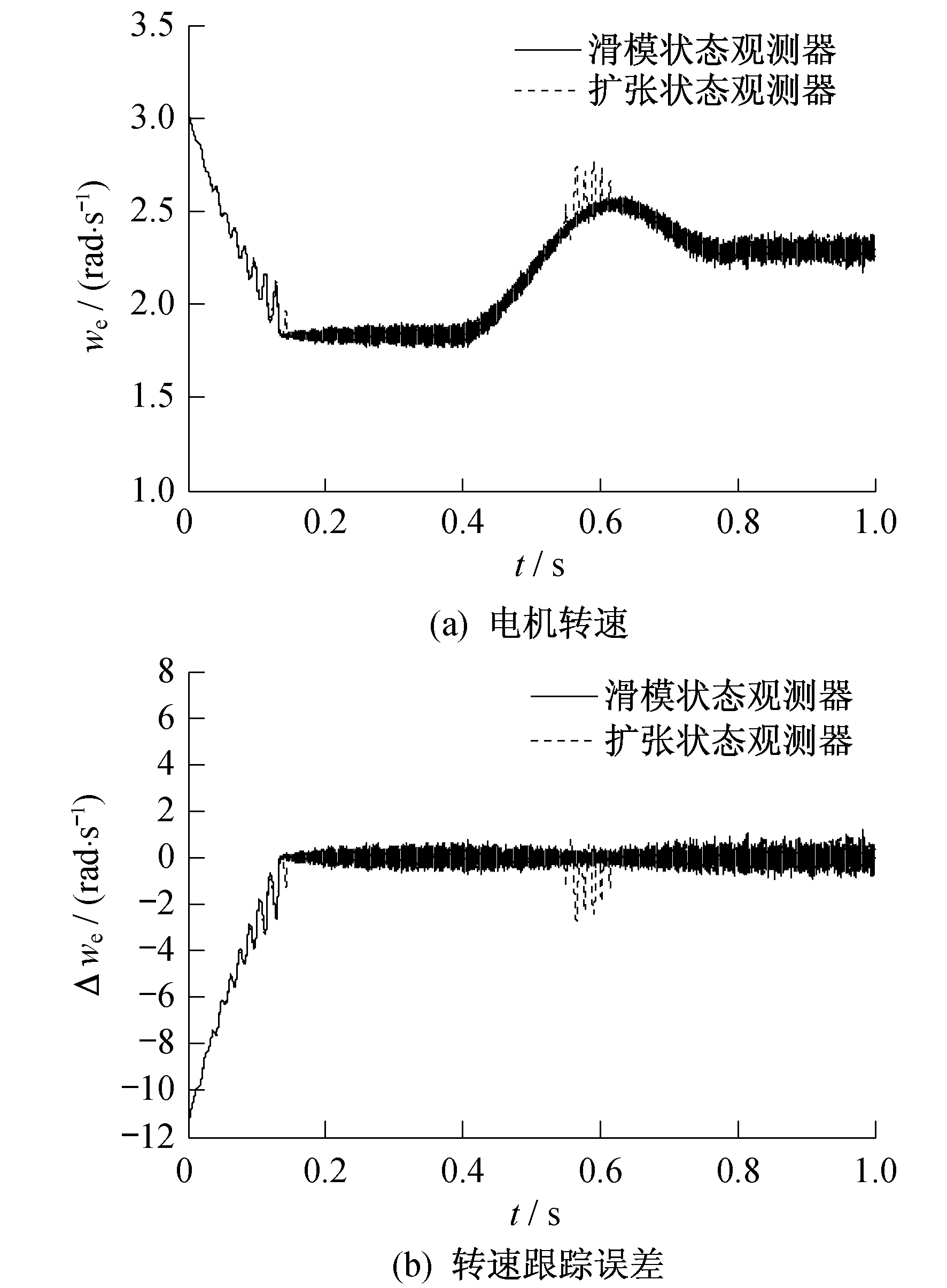
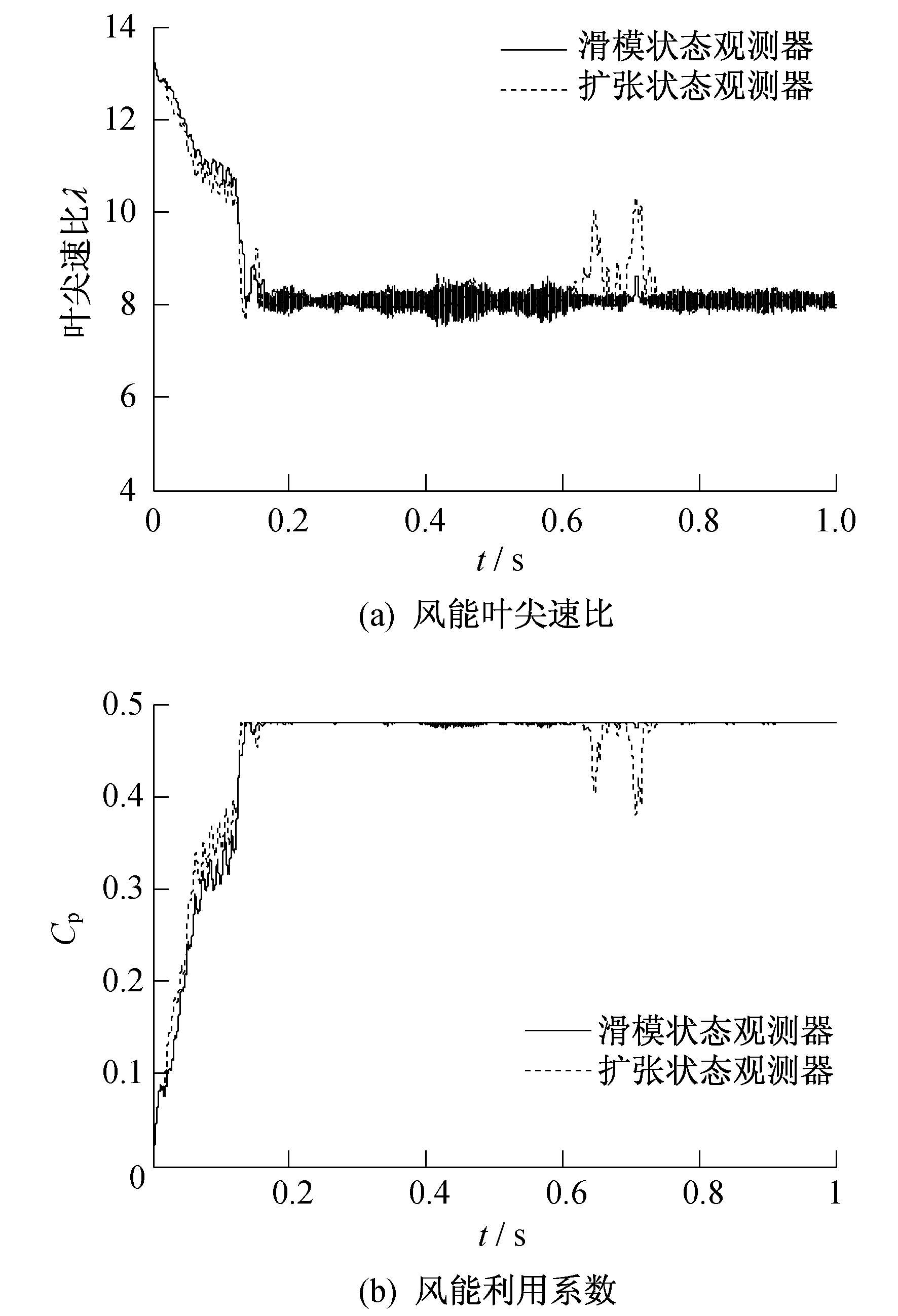
设计3个算例仿真, 在不同风速条件下验证滑模状态观测器和基于状态观测器的滑模自适应控制器的有效性。算例1是在随机风速变化下, 风速变化较快、波动较大时, 验证观测器的观测效果。算例2是在平滑风速下, 风速变化较为缓慢、波动较小时, 验证观测器的观测效果。算例3是在随机风速下验证控制器的控制效果。仿真结果表明, 所设计的滑模状态观测器具有较好的鲁棒性, 对于不同程度的干扰都有较好的平抑效果; 同时, 基于状态观测器的滑模自适应控制器能最大限度地利用风能。在本仿真算例中, 风机和电机的参数选取如表 1和表 2所示。
表 1
系统仿真中的风机参数
| 参数 | 数值 |
| 额定功率$P_{\mathrm{N}} / \mathrm{MW}$ | 2 |
| 额定风速$v_{\mathrm{wN}} /\left(\mathrm{m} \cdot \mathrm{s}^{-1}\right)$ | 13 |
| 风机半径$R / \mathrm{m}$ | 35.325 |
| 空气密度$\rho /\left(\mathrm{kg} \cdot \mathrm{m}^{-3}\right)$ | 1.225 |
| 最佳叶尖速比$\lambda$ | 8.1 |
| 切入风速$v_{\text {cutin }} /\left(\mathrm{m} \cdot \mathrm{s}^{-1}\right)$ | 5 |
| 切出风速$v_{\text {cutout }} /\left(\mathrm{m} \cdot \mathrm{s}^{-1}\right)$ | 24 |
| 风能系数$C_{P \max }$ | 0.48 |
表 2
系统仿真中的电机参数
| 参数 | 数值 |
| 额定功率$P_{\mathrm{N}} / \mathrm{MW}$ | 2 |
| 转动惯量$J /\left(\mathrm{kg} \cdot \mathrm{m}^{2}\right)$ | 500 |
| 转子磁链$\psi_{\mathrm{a}} / \mathrm{Wb}$ | 1.67 |
| 交直轴电感$L / \mathrm{H}$ | 0.003 |
| 交、直轴电阻$R_{\mathrm{a}} / \Omega$ | 0.01 |
| 定子额定电压$U_{\mathrm{d}} / \mathrm{V}$ | 750 |
| 极对数$p$ | 32 |
3.1 算例仿真1
3.2 算例仿真2
3.3 算例仿真3
4 结论
(1) 针对传统无速度传感器的风电系统变量难以测量的问题, 设计了一种滑模状态观测器, 能很好地估计系统转速跟踪误差。
(2) 基于估计值设计了基于滑模状态观测器的滑模自适应最大功率点跟踪控制器, 补偿系统扰动, 相比于传统的最大功率点跟踪控制具有更好的鲁棒性。
参考文献
-
[1]独立光储直流微电网分层协调控制[J]. 电力系统保护与控制, 2017, 45(8): 37-45. DOI:10.7667/PSPC160589
-
[2]一种新型结构变速恒频风力发电机组系统及其控制策略[J]. 电工技术学报, 2013, 28(7): 80-86. DOI:10.3969/j.issn.1000-6753.2013.07.011
-
[3]10 MW变速直驱型风力发电机组的建模及MATLAB仿真[J]. 电力系统保护与控制, 2011, 39(24): 8-15. DOI:10.3969/j.issn.1674-3415.2011.24.002
-
[4]基于RT-LAB兆瓦级PMSG实时仿真及最大功率跟踪[J]. 电气开关, 2018(4): 63-66. DOI:10.3969/j.issn.1004-289X.2018.04.015
-
[5]采用梯度估计的风力发电系统最优转矩最大功率点追踪效率优化[J]. 中国电机工程学报, 2015, 35(10): 1-8.
-
[6]MEHARRAR A, TIOURSI M, HATTI M, et al. A variable speed wind generator maximum power tracking based on adaptative neuro-fuzzy inference system[J]. Expert Systems with Applications, 2011, 38(2): 7659-7664.
-
[7]WEI C, ZHANG Z, QIAO W, et al. An adaptive network-based reinforcement learning method for MPPT control of PMSG wind energy conversion systems[J]. IEEE Transactions on Power Electronics, 2016, 31(11): 7837-7848. DOI:10.1109/TPEL.2016.2514370
-
[8]基于无风速传感器的永磁直驱风力发电系统的直接转矩最大功率跟踪控制[J]. 电工技术学报, 2014, 29(1): 132-137.
-
[9]基于扩张状态观测的永磁直驱风力发电系统MPPT自适应滑模控制[J]. 电力系统保护与控制, 2014, 42(18): 58-65. DOI:10.7667/j.issn.1674-3415.2014.18.010
-
[10]直驱式永磁同步风力发电动态特性的研究[J]. 电力系统保护与控制, 2012, 40(14): 38-43. DOI:10.7667/j.issn.1674-3415.2012.14.007
-
[11]永磁同步电机调速系统的滑模控制[J]. 电工技术学报, 2009, 24(9): 71-77. DOI:10.3321/j.issn:1000-6753.2009.09.011
-
[12]永磁风力发电系统及其功率变换技术[J]. 电工技术学报, 2012, 27(11): 1-13.
-
[13]风力发电三相PWM变换器的建模与控制[J]. 电网技术, 2009, 33(20): 43-48.
-
[14]基于积分时变滑模控制的永磁同步电机调速系统[J]. 电工技术学报, 2011, 26(6): 56-61.
-
[15]风气互补发电系统的孤岛运行仿真[J]. 太阳能学报, 2013, 34(2): 207-212. DOI:10.3969/j.issn.0254-0096.2013.02.005
-
[16]LIAO Y, HE J B, YAO J, et al. Power smoothing control strategy of direct-driven permanent magnet synchronous generator for wind turbine with pitch angle control and torque dynamic control[J]. Proceedings of the CSEE, 2009, 29(18): 71-77.
-
[17]柴储混合电力系统的频率协调控制策略[J]. 上海电力学院学报, 2018, 34(6): 577-580.
-
[18]高为炳.变结构控制理论基础[M].北京: 科学出版社, 1990: 85-123.
-
[19]GAO W B, WANG Y F, HOMAIFA A. Discrete time variable structure control systems[J]. IEEE Transactions on Industrial Electronics, 1995, 42(2): 117-122. DOI:10.1109/41.370376
-
[20]GAO W B. Variable structure control theory and design methods[M]. Beijing: Science and Technology Press, 1996: 90-133.