|
|
|
发布时间: 2019-12-10 |
|
|
|
|
收稿日期: 2019-10-07
基金项目: 国家自然科学基金青年科学基金(51607111);上海市科学技术委员会地方院校能力建设项目(15160500800)
中图法分类号: TM715
文献标识码: A
文章编号: 1006-4729(2019)06-0573-07
|
摘要
在楼宇短期负荷预测中, 针对单一预测模型难以充分学习负荷时间序列中的特性问题, 提出了一种基于自回归差分移动平均-长短期记忆神经网络(ARIMA-LSTM)组合模型的楼宇负荷预测方法。首先, 根据灰色关联度选取相似日时间序列数据为训练样本; 然后, 利用ARIMA模型预测负荷, 并将原始数据和ARIMA预测数据之间的误差视为非线性分量; 最后, 通过LSTM神经网络对误差序列进行校正, 得到楼宇短期负荷的最终预测值。通过对上海市某楼宇的预测效果分析, 并将其与ARIMA模型、LSTM模型和ARIMA-SVM组合模型进行对比, 验证了所提方法能够有效控制预测误差, 提高楼宇负荷预测精度。
关键词
楼宇短期负荷预测; 自回归差分移动平均模型; 长短期记忆神经网络; 时间序列; 灰色关联度
Abstract
Aiming at the problem that a single forecasting model is difficult to fully learn the characteristics of the time series, this paper proposes a combined model based on ARIMA-LSTM forecasting method.Firstly, the data of similar daily time series are selected as training samples according to the grey correlation degree; then the load is predicted by ARIMA, and the error between the original data and the ARIMA prediction data is regarded as a nonlinear component.The Long-Short Term Memory Network(LSTM) corrects the error sequence to obtain the final predicted value of the building's short-term load.Through the analysis of the prediction effect of a building in Shanghai, and the comparison with ARIMA, LSTM model and ARIMA-SVM combined model, it is proved that the method can effectively control the prediction error and improve the building load forecasting accuracy.
Key words
short-term load forecasting of buildings; autoregressive integrated moving average model(ARIMA); long-short term memory(LSTM); time series; grey correlation degree
随着我国城镇化建设的高速发展, 楼宇建筑能耗的比重也将持续上升。为了缓解能源危机、改善环境恶化, 降低楼宇能耗、提高能效管理已成为业界重点关注的问题。这使得楼宇负荷预测成为泛在电力物联网建设的一项重要研究内容。精确的负荷预测, 可以为楼宇能效管理系统制定用电需求响应和负荷调度规划提供决策依据, 有利于优化供需平衡, 提高用电设备的利用率, 对智能电网的节能调度和稳定运行具有重要意义[1]。
目前, 国内外对短期负荷预测模型的研究主要分为两类。一类是线性模型, 文献[2]运用协整理论并考虑带输入变量温度序列, 建立了ARIMAX模型来进行短期负荷预测, 极大地提高了预测精度; 文献[3]采用regARIMA模型对消除离群值影响的月负荷数据进行预测, 改善了预测效果。上述模型的研究对象均为地区负荷, 其变化规律具有较强的周期性, 若细化到单个楼宇负荷时, 由于样本数据的波动性和随机性较大, 采用线性模型将会增大预测误差。另一类是非线性模型, 文献[4]采用DBN-SVM组合模型来预测未来小时负荷, 其预测精度较高, 但忽略了不同时间序列负荷数据间的关系; 文献[5]将注意力机制(Attention)与长短期记忆神经网络(Long-Short Term Memory, LSTM)相结合, 突出对负荷预测起关键作用的输入特征, 建立多步长、多变量的短期负荷预测模型, 有效提高了预测精度。上述研究均对非线性模型进行了优化, 其预测效果良好。作为时间序列的楼宇负荷, 由于预测模型的误判、拟合不足或过度拟合等问题, 采用单一人工神经网络进行建模的效果不一定最好[6]。因此, 组合线性和非线性模型可以提高系统的准确性[7]。
同时, 在利用线性和非线性组合模型进行负荷预测的研究中, 文献[8-10]采用组合预测方法分别处理时间序列和误差序列, 提高了预测的精度, 其中误差序列是通过原始序列和线性预测之间的差异获得的。根据BOX G E和JENKINS G M设计的自回归差分移动平均(Autoregressive Integrated Moving Average, ARIMA)模型表明, 误差序列不应该呈现线性相关[11]。因此, 利用非线性模型来处理误差序列中可能存在的一些非线性关系是合理的。
为解决单一模型无法同时兼顾时间序列数据的线性和非线性关系的问题, 本文提出了一种基于ARIMA-LSTM组合模型的楼宇短期负荷预测方法。首先, 考虑气象因素和日期类型对楼宇负荷的影响, 利用灰色关联度分析法选取输入特征量的关键影响因素; 然后, 获取相似日样本数据; 同时, 综合考虑楼宇负荷序列的线性和非线性特点, 利用线性ARIMA模型进行预测; 最后, 采用LSTM模型进行误差矫正。以上海市某楼宇为例, 通过比较本文方法和其他方法的预测结果, 验证本文预测方法的有效性。
1 基于灰色关联度的相似日选择
1.1 负荷影响因素分析
气象因素对楼宇短期负荷预测的主要影响因素有气温、风速、相对湿度、降雨量等[13]。随着这些因素的变化, 楼宇负荷会发生剧烈变化。同时, 对于楼宇建筑负荷而言, 工作日、非工作日(周六、周日和节假日)的电力负荷量也是差异显著。
作为计算灰色关联度的样本, 本文将选择如下日特征因素:日期类型、最高气温、最低气温、风速、相对湿度、降雨量。其映射值如表 1所示。
表 1
日特征因素的映射值
| 日特征因素 | 标识符号 | 映射值 |
| 日期类型 | d | |
| 最高气温 | tmax | |
| 最低气温 | tmin | |
| 风速 | w | |
| 相对湿度 | h | |
| 降雨量 | r |
1.2 数据预处理
由于负荷与各影响因子的量纲不同, 直接将不同量纲的数据输入预测模型进行训练, 容易造成模型不收敛, 进而影响负荷预测的准确度。文献[15]的研究表明, 对样本数据进行归一化处理可以提高模型的收敛速度。因此, 本文将采用最大最小归一化处理, 将各影响因素样本数据转换到[0, 1]内, 其计算公式为
| $ X^{*}=\frac{X-X_{\min }}{X_{\max }-X_{\min }} $ | (1) |
式中:X*——归一化后的值;
X——样本序列值;
Xmin——X中的最小值;
Xmax——X中的最大值。
1.3 灰色关联度分析
针对楼宇负荷影响因素较多的情况, 本文采用灰色关联度分析法, 利用气象因素、日期类型与负荷序列之间发展趋势的相似或相异程度来选取关键影响因素。
设待预测日的特征向量为Yj={y1, y2, y2, …, ym}, j=1, 2, 3, …, m, 第i个历史日的特征向量为Xij={xi1, xi2, xi3, …, xim}, i=1, 2, 3, …, n, 其中m为影响因子个数, n为历史记录天数。以待预测日特征向量Yj为参考序列, 历史日特征向量Xij为比较序列, 则灰色关联度的计算步骤如下。
首先, 求两极的最大差和最小差, 公式分别为
| $ Z=\max\limits _{1 \leqslant i \leqslant n} \max\limits _{1 \leqslant j \leqslant m} \left| \boldsymbol{Y}_{j}-\boldsymbol{X}_{i j}\right| $ | (2) |
| $ Z=\min\limits _{1 \leqslant i \leqslant n} \min\limits _{1 \leqslant j \leqslant m} \left| \boldsymbol{Y}_{j}-\boldsymbol{X}_{i j} \right|$ | (3) |
然后, 记βij为Yj在Xij处的关联系数, 则
| $ \beta_{i j}=\frac{z+\rho Z}{\Delta Z_{i j}+\rho Z} $ | (4) |
式中:ρ——分辨系数, 一般在[0, 1]之间取值, 取ρ=0.5;
ΔZij=|Yj-Xij|。
计算各影响因子的灰色关联权重为
| $ \mu_{j}=\frac{\frac{1}{n} \sum\limits_{i=1}^{n} \beta_{i j}}{\sum\limits_{j=1}^{m} \frac{1}{n} \sum\limits_{i=1}^{n} \beta_{i j}} $ | (5) |
最后, 可计算灰色关联度为
| $ r_{i}=\frac{1}{m} \sum\limits_{j=1}^{m}\left(\mu_{j} \beta_{i j}\right), i=1,2,3, \cdots, n $ | (6) |
1.4 相似日选择
挑选出关键影响因素后, 以该因素数据序列为对象来选择楼宇负荷预测的相似日。余弦距离是最常用的相似度量方法, 利用向量夹角的余弦值即向量方向来刻画相似度, 可以不受维度影响, 范围限定在[1, 2]内。因此, 本文选用余弦距离进行相似度量。
设某两天关键影响因素数据序列为Lp=[lp1, lp2, lp3, …, lpt]和Lq=[lq1, lq2, lq3, …, lqt], t=1, 2, 3, …, n, 则两负荷日之间的余弦距离为
| $ \cos F_{p q}=\frac{\sum\limits_{k=1}^{t} L_{p k} L_{q k}}{\sqrt{\sum\limits_{k=1}^{t} L_{p k}^{2}} \sqrt{\sum\limits_{k=1}^{t} L_{q k}^{2}}} $ | (7) |
其中, cos Fpq的数值越大, 则影响因素序列曲线形态差异越小, 负荷的相似度也就越高。
2 基于ARIMA-LSTM的负荷预测模型
楼宇负荷序列中含有线性分量和非线性分量, 仅采用单一模型难以充分学习负荷序列的特性。本文采用线性和非线性模型组合的方法来预测楼宇负荷, 利用线性模型ARIMA拟合时间序列的负荷数据, 最大程度地消除数据中的线性成分, 然后利用非线性模型LSTM来预测线性模型无法拟合的误差序列, 并以此来校正最终预测结果, 充分发挥了线性模型和非线性模型的预测性能。
2.1 线性ARIMA模型
ARIMA模型是由BOX G E和JENKINS G M[16]提出, 其在时间序列分析中的能力和灵活性已得到广泛证明。ARIMA(p, d, q)模型由p阶自回归模型AR(p)、q阶移动平均模型MA(q)和产生平稳序列的差分次数d组成, 通过差分处理将非平稳的时间序列平稳化, 然后对因变量的滞后值以及随机误差项的当前值和滞后值进行回归。本文根据赤池信息准则(Akaike Information Criterion, AIC)来确定模型的最佳阶次, 最终建立ARIMA(2, 1, 2)模型, 满足了模型平稳性要求, 并有效地消除了预测中存在的随机波动。
2.2 非线性LSTM模型
神经网络是一种可用于逼近任何非线性函数的有效工具, 在处理非线性问题时受到广泛使用[17]。其中, 循环神经网络(Recurrent Neural Networks, RNN)由SATHASIVAM S[18]于1982年提出, 主要用于处理和预测时间序列数据, 通过时间反向传播或实时循环学习算法进行训练。
但是, 由于实际中序列过长会导致优化时出现梯度消失或爆炸的问题, 经常造成训练结果较差。HOCHREITER S和SCHMIDHUBE J[19]提出了一种长短期记忆神经网络(LSTM), 作为RNN的变体, 专门用于克服梯度消失问题, 能够长时间存储信息。
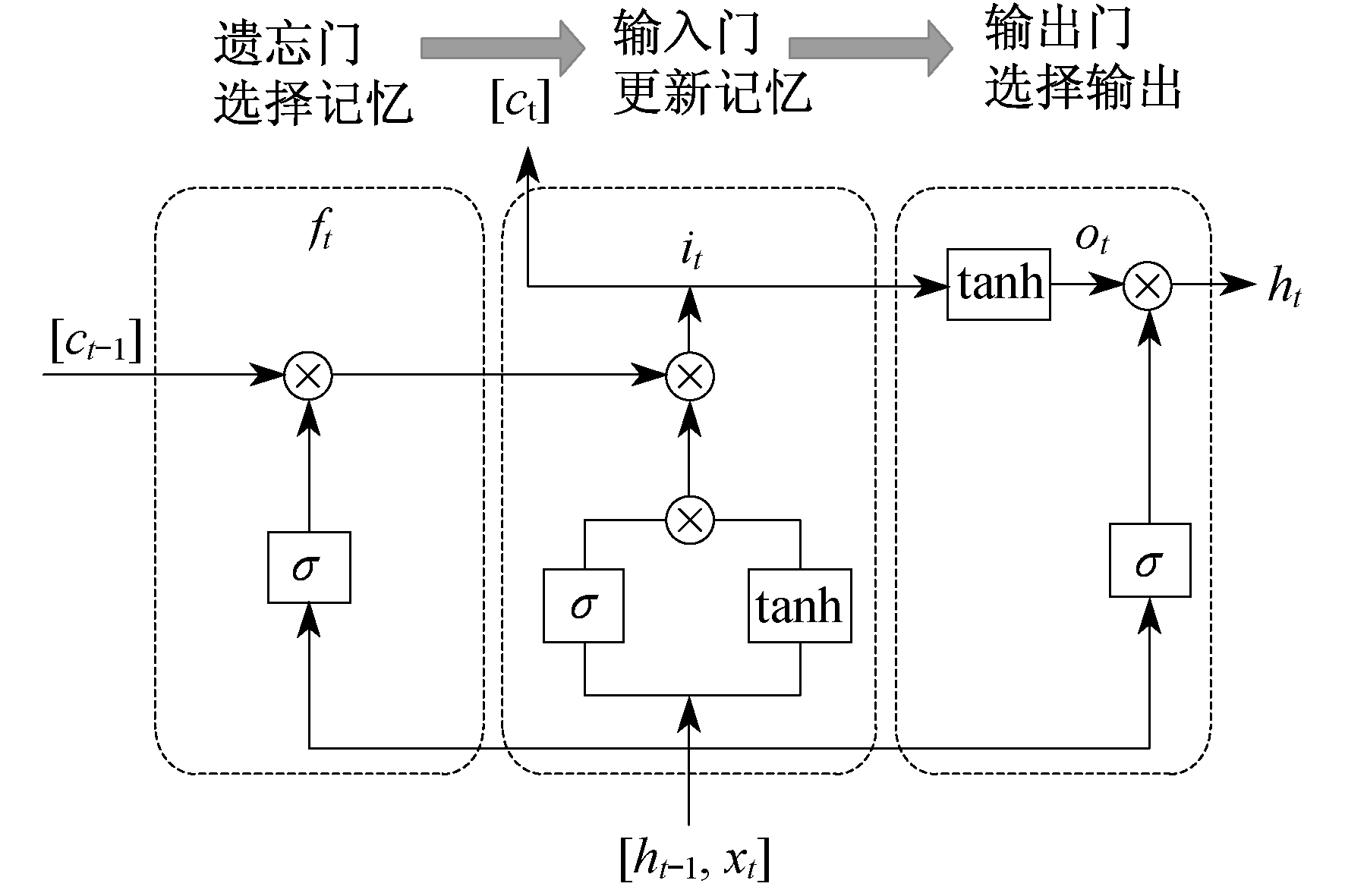
LSTM神经网络由输入层、输出层和介于其间的多个隐藏层构成。其中, 隐藏层被构造成具有记忆功能的单元, 每个单元包含了3个门, 分别是遗忘门(Forget Gate)、输入门(Input Gate)和输出门(Output Gate)[20]。标准的LSTM神经网络记忆单元如图 1所示。
在遗忘门中, 每个输入xt, 前一时刻单元输出ht-1和前一时刻单元状态ct-1共同决定了状态记忆单元的遗忘部分; 输入门中, 在sigmoid和tanh函数的激活下, 将单元状态ct-1更新到ct; 输出门中, 更新后的单元状态ct再一次通过sigmoid和tanh函数, 有选择地输出ht。LSTM神经网络单元可以用以下方程组进行定义:
| $f_{t}=\sigma\left(\boldsymbol{W}_{\mathrm{f}}\left[h_{t-1}, x_{t}\right]+b_{\mathrm{f}}\right)$ | (8) |
| $i_{t}=\sigma\left(\boldsymbol{W}_{\mathrm{i}}\left[h_{t-1}, x_{t}\right]+b_{\mathrm{i}}\right)$ | (9) |
| $o_{t}=\sigma\left(\boldsymbol{W}_{\mathrm{o}}\left[h_{t-1}, x_{t}\right]+b_{\mathrm{o}}\right)$ | (10) |
| $g_{t}=\tanh \left(\boldsymbol{W}_{\mathrm{g}}\left[h_{t-1}, x_{t}\right]+b_{\mathrm{g}}\right)$ | (11) |
| $c_{t}=g_{t} \cdot i_{t}+f_{t} \cdot c_{t-1}$ | (12) |
| $h_{t}=o_{t} \cdot \tanh \left(c_{t}\right)$ | (13) |
式中:ft, it, ot, gt——遗忘门, 输入门, 输出门, 备选状态;
ct, ht——当前输入更新后的单元状态, 当前的预测或输出状态;
Wf, Wi, Wo, Wg——相应门的权重矩阵;
bf, bi, bo, bg——各相应门的偏移量;
σ——sigmoid激活函数;
tanh——双曲正切激活函数;
·——向量中元素按位相乘。
2.3 ARIMA-LSTM组合模型
设原始负荷数据集为H=[h1, h2, h3, …, hn], 利用ARIMA模型得到H的历史数据拟合序列A=[A1, A2, A3, …, An]和预测序列PA=[P1, P2, P3, …, Pt], 将拟合值与负荷实际值相比较, 得到拟合误差序列ΔA=[ΔA1, ΔA2, ΔA3, …, ΔAn], 计算公式为
| $\Delta A_{i}=h_{i}-A_{i}, i=1,2,3, \cdots, n$ | (14) |
拟合误差序列ΔA在一定程度上减少了线性分量的影响, 使得负荷的非线性特性较强。神经网络模型的非线性学习性能适用于拟合误差序列的预测校正, 因此本文利用LSTM神经网络对拟合误差序列ΔA进行预测, 得到非线性误差预测项ΔLt, 其计算公式为
| $\Delta L_{t}=f\left(\Delta A_{t-1}, \Delta A_{t-2}, \cdots, \Delta A_{t-n}\right)+\varepsilon_{t}$ | (15) |
式中:f(·)——LSTM的非线性建模;
εt——随机误差, 无法预测。
将预测值ΔLt作为负荷误差预测结果, 进一步学习误差序列的非线性特征, 输出一个稳定有效的预测结果并进行误差校正, 最后得到ARIMA-LSTM组合模型的预测结果为
| $P_{\mathrm{AL} t}=P_{t}+\Delta L_{t}$ | (16) |
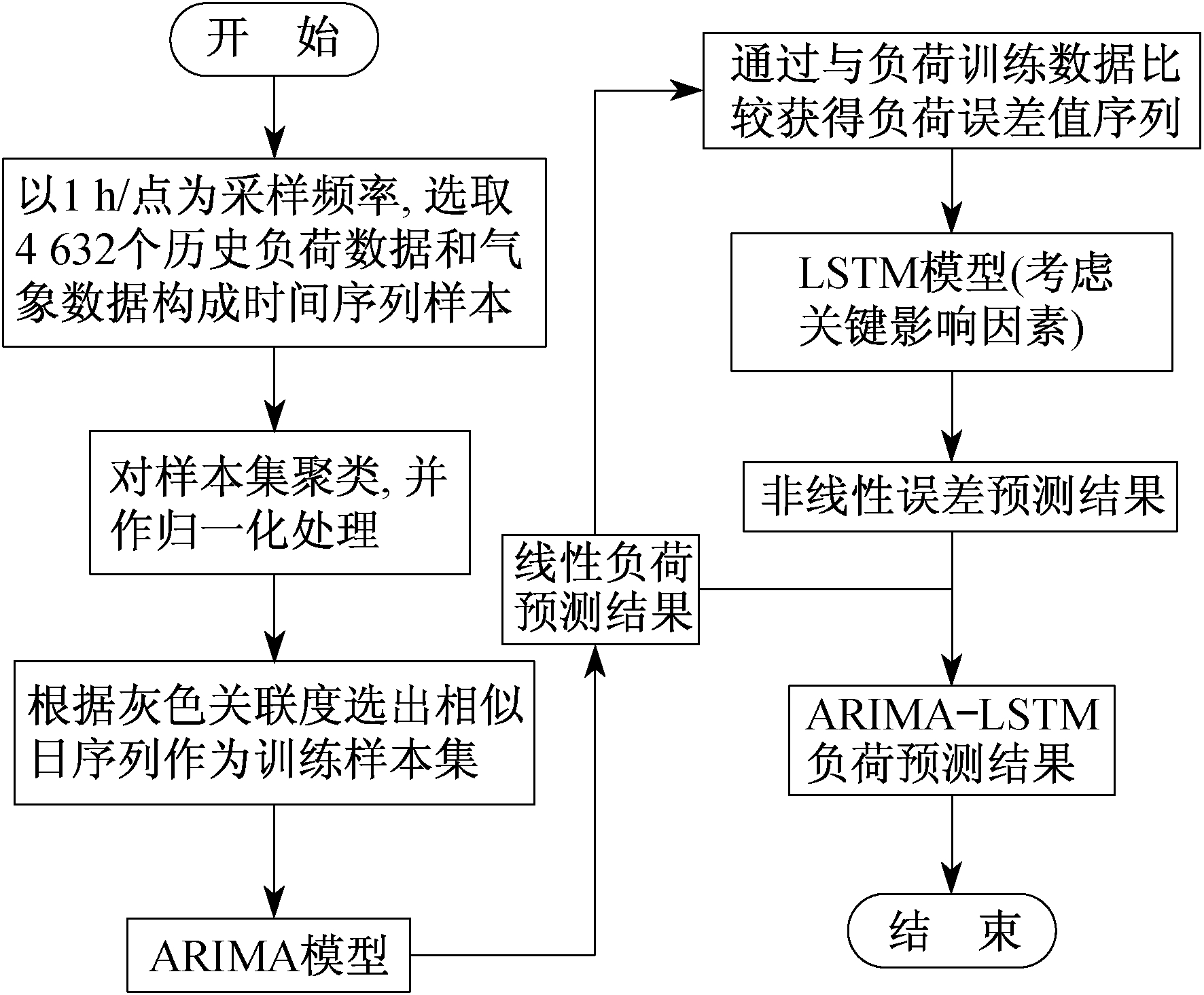
本文提出的ARIMA-LSTM组合模型预测步骤为:将相似日负荷训练集数据输入到ARIMA模型中, 得到线性负荷预测值; 比较负荷训练数据和线性拟合数据, 得到拟合误差序列; 结合相似日的关键气象因素数据, 利用LSTM模型预测拟合误差序列; 将线性拟合预测值与非线性误差预测值相加, 得出组合模型最终的负荷预测结果。
3 算例分析
3.1 数据来源与预测流程
本文以上海市某楼宇2011年9月2日至2012年3月12日的历史负荷数据为样本, 对该楼宇2012年3月13日至3月19日的短期负荷进行预测。实验数据包含负荷数据、气象数据和日期类型数据, 采样间隔均为1 h, 每天记录24个数据点。利用灰色关联度相似日选择和ARIMA-LSTM组合模型进行楼宇短期负荷预测的具体流程如图 2所示。
3.2 预测结果误差评估指标
选用平均绝对误差(MAE)、均方根误差(RMSE)和平均绝对百分比误差(MAPE)等统计指标对模型的负荷预测性能进行评价。其计算公式分别为
| $ e_{\mathrm{MAE}}=\frac{1}{N} \sum\limits_{t=1}^{N} \left| P_{t}-\hat{P}_{t} \right| $ | (17) |
| $ e_{\mathrm{RMSE}}=\sqrt{\frac{1}{N} \sum\limits_{t=1}^{N}\left(P_{t}-\hat{P}_{t}\right)^{2}} $ | (18) |
| $ e_{\mathrm{MAPE}}=\frac{1}{N} \sum\limits_{t=1}^{N}\left|\frac{P_{t}-\hat{P}_{t}}{P_{t}}\right|^{2} \times 100 \% $ | (19) |
式中:N——预测点总个数;
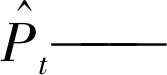 负荷实际值;
负荷实际值;
Pt——负荷预测值。
3.3 实验结果与分析
采用归一化方法去除负荷数据和气象数据的量纲, 并计算负荷与各影响因素之间的灰色关联度, 结果如表 2所示。从表 2可以看出, 日期类型和气温对负荷的影响较大, 故本文只选取这两项作为关键影响因素。
表 2
各影响因素的灰色关联度结果
| 影响因素名称 | 数据范围 | 灰色关联度 |
| 气温 | [0, 1] | 0.6031 |
| 日期类型 | [0, 1] | 0.1985 |
| 降雨量 | [0, 1] | 0.0676 |
| 风速 | [0, 1] | 0.0614 |
| 相对湿度 | [0, 1] | 0.0379 |
以2012年3月13日为例, 采用余弦距离法选出与预测日的日期类型和气温情况最相近的15个历史日作为相似日, 如表 3所示。将所选取的15个相似日的日期类型数据、气温数据和负荷数据作为组合预测模型的训练集。经多次实验确定ARIMA模型的参数为(2, 1, 2), LSTM神经网络的隐藏层有50个神经元, 训练块大小(batch_size)为32, 训练次数(epochs)为50。
表 3
2012年3月13日的相似日选择结果
| 日期 | 余弦距离相似度 | 日期 | 余弦距离相似度 |
| $2012-03-08$ | 1.9024 | $2012-03-06$ | 1.6536 |
| $2012-02-28$ | 1.8852 | $2012-03-12$ | 1.6231 |
| $2012-03-02$ | 1.8641 | $2012-02-29$ | 1.6025 |
| $2012-03-09$ | 1.8294 | $2012-02-23$ | 1.5846 |
| $2012-02-16$ | 1.7562 | $2012-03-07$ | 1.5549 |
| $2012-03-05$ | 1.7357 | $2012-02-24$ | 1.5308 |
| $2012-03-01$ | 1.7086 | $2012-02-22$ | 1.5128 |
| $2012-02-20$ | 1.6804 |
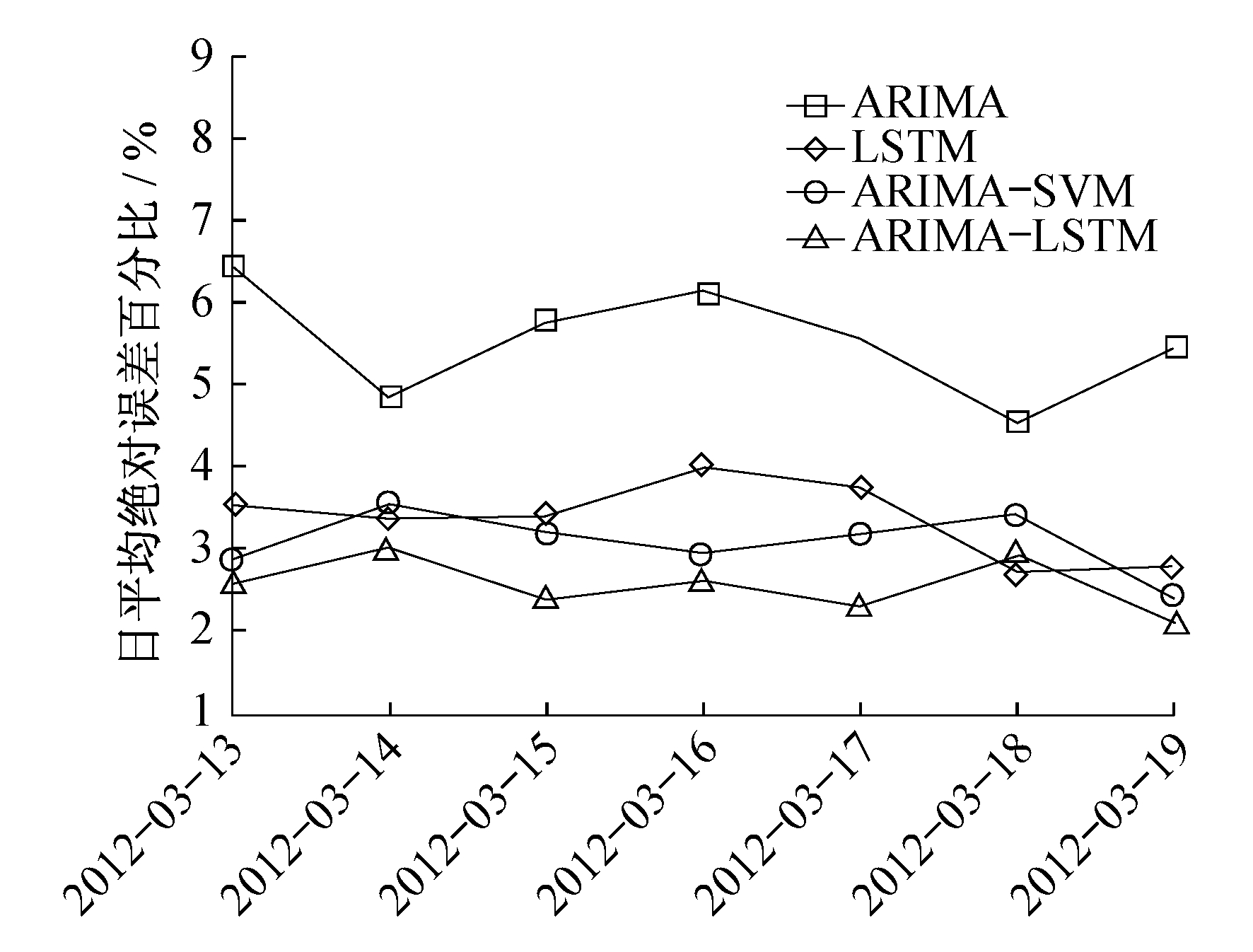
为比较不同模型的预测效果, 本文采用ARIMA模型、LSTM模型、ARIMA-SVM组合模型和ARIMA-LSTM组合模型, 分别对该办公楼宇2012年3月13日至19日中每天24个时刻(时间间隔1 h)的负荷进行预测, 并计算出每天的平均绝对误差eMAPE, 各模型的预测结果误差曲线如图 3所示。
同时, 为进一步分析不同预测模型的预测效果, 表 4列出了各模型在连续7个预测日的平均绝对误差结果。由表 4可以看出, ARIMA模型的平均绝对误差为5.53%, 远大于其他3种模型, 而ARIMA-LSTM模型预测连续7天负荷的eMAPE为2.45%, 小于其他3种模型, 预测效果最好。
表 4
4种模型的预测效果对比
| 预测模型 | $e_{\mathrm{MAPE}} / \%$ | $e_{\mathrm{MAE}} / \mathrm{kW}$ | $e_{\mathrm{RMSE}} / \mathrm{kW}$ |
| ARIMA | 5.53 | 143.26 | 190.46 |
| LSTM | 3.37 | 129.86 | 146.19 |
| ARIMA-SVM | 3.09 | 93.35 | 117.03 |
| ARIMA-LSTM | 2.45 | 85.36 | 101.91 |
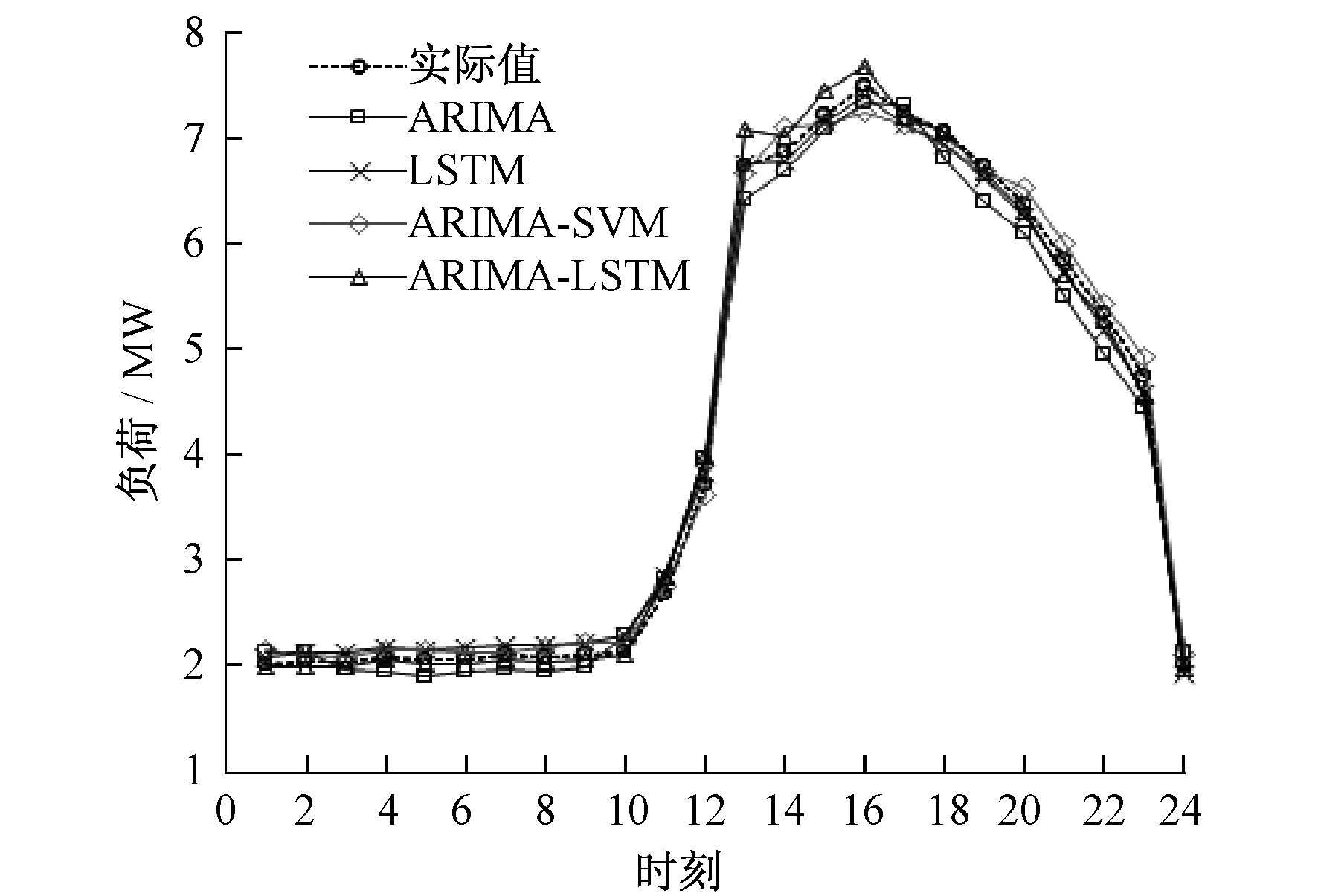
为进一步分析模型的性能, 利用4种模型分别对2012年3月下旬的某一天进行负荷预测, 将各负荷模型的预测值与实际负荷数据进行比较, 计算出各个时刻负荷预测的绝对误差百分比, 如图 4所示。由图 4可以看出, 各负荷预测模型的预测数值均出现不同程度的偏差。
结合图 4中各模型负荷预测的误差百分比分布, 利用统计学原理, 分别统计出各时刻预测误差小于3%的概率, 如表 5所示。由表 5可以看出:本文所提出的ARIMA-LSTM组合模型的预测误差小于3%的概率要远高于其他3种模型, 表明该方法在负荷预测上的准确度更高; 同时, ARIMA-LSTM组合模型的平均绝对误差eMAPE为2.02%, 平均绝对误差eMAE为78.85 kW, 均方根误差eRMSE为97.91 kW, 均小于其他模型, 由此可见ARIMA-LSTM组合模型在控制预测误差方面效果更理想。
表 5
4种模型预测的误差概率统计情况
| 预测模型 | 误差预测模型小于3 %的概率/% | eMAPE/% | eMAE/kW | eRMSE/kW |
| ARIMA | 12.5 | 5.15 | 190.20 | 212.79 |
| LSTM | 45.8 | 3.44 | 107.93 | 112.92 |
| ARIMA-SVM | 54.2 | 2.82 | 98.01 | 108.57 |
| ARIMA-LSTM | 87.5 | 2.02 | 78.85 | 97.91 |
4 结语
本文提出了一种基于ARIMA-LSTM组合模型的楼宇短期负荷预测方法, 通过灰色关联度和余弦距离筛选出相似日训练样本数据, 然后结合ARIMA模型的线性特点和LSTM模型的非线性优势预测楼宇短期负荷, 有效提高了预测精度, 从而为智能楼宇能量管理系统提供了更准确的数据基础。但文中仅对单一楼宇进行了研究, 未来可考虑结合并行技术和迁移学习实现对海量楼宇用户数据的预测研究, 提高运算效率。
参考文献
-
[1]MOCANU E, NGUYEN P H, GIBESCU M, et al. Deep learning for estimating building energy consumption[J]. Sustainable Energy, Grids and Networks, 2016, 6(2): 91-99.
-
[2]基于ARIMAX模型的夏季短期电力负荷预测[J]. 电力系统保护与控制, 2015, 43(4): 108-114. DOI:10.7667/j.issn.1674-3415.2015.04.017
-
[3]基于regARIMA模型的月度负荷预测效果研究[J]. 中国电力, 2018, 51(5): 166-171.
-
[4]基于信息融合的电力大数据可视化预处理方法[J]. 广东电力, 2016, 29(12): 10-14. DOI:10.3969/j.issn.1007-290X.2016.12.003
-
[5]电力市场中基于Attention-LSTM的短期负荷预测模型[J]. 电网技术, 2019, 43(5): 1745-1751.
-
[6]BABU C N, REDDY B E. A moving-average filter based hybrid ARIMA-ANN model for forecasting time series data[J]. Appl Soft Comput, 2014(23): 27-38.
-
[7]DE MATTOS N, PAULO S G, CAVALCANT I, et al. Nonlinear combination method of forecasters applied to PM time series[J]. Pattern Recognit Lett, 2017(6): 65-72.
-
[8]基于GA-RBF神经网络的电力系统短期负荷预测[J]. 上海电力学院学报, 2019, 35(3): 205-210.
-
[9]DE MATTOS N P S, FERREIRA T A, LIMA A R, et al. A perturbative approach for enhancing the performance of time series forecasting[J]. Neural Netw, 2017(28): 114-124.
-
[10]RUIZ-AGUILAR J, TURIAS I, JIMÉNEZ-COME M. Hybrid approaches based on SARIMA and artificial neural networks for inspection time series forecasting[J]. Transp Res, 2014(3): 1-13.
-
[11]BOX G E, JENKINS G M. Time series analysis: forecasting and Control[M]. San Fransisco, CA, USA: John Wiley and Sons Inc, 2015: 712-713.
-
[12]基于气温与日期类型的改进BP网络热负荷预测[J]. 系统仿真学报, 2018, 30(4): 1464-1472.
-
[13]基于PSO改进的T-S模糊神经网络短期电力负荷预测研究[J]. 上海电力学院学报, 2017, 33(4): 325-330.
-
[14]基于灰色关联与模糊聚类分析的负荷预处理方法[J]. 电测与仪表, 2017, 54(11): 36-42. DOI:10.3969/j.issn.1001-1390.2017.11.007
-
[15]基于数据挖掘技术和支持向量机的短期负荷预测[J]. 电测与仪表, 2016, 53(10): 62-67. DOI:10.3969/j.issn.1001-1390.2016.10.011
-
[16]CONTIER J, ESPINOLA R, NOGALES F J, et al. ARIMA models to predict next-day electricity price[J]. IEEE Transactions on Power Systems, 2003, 18(3): 1014-1020. DOI:10.1109/TPWRS.2002.804943
-
[17]KOURENTZES N, BARROW D K, CRONE S F. Neural network ensemble operators for time series forecasting[J]. Expert Syst Appl, 2014, 41(9): 4235-4244. DOI:10.1016/j.eswa.2013.12.011
-
[18]SATHASIVAM S. Logic learning in hopfield networks[J]. Modern Applied Science, 2006, 2(3): 208-209.
-
[19]HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735
-
[20]基于深度学习LSTM网络的短期电力负荷预测方法[J]. 电子技术, 2018, 47(1): 39-41. DOI:10.3969/j.issn.1000-0755.2018.01.011