|
|
|
发布时间: 2020-04-10 |
|
|
|
|
收稿日期: 2019-12-23
基金项目: 国家自然科学基金(51507098)
中图法分类号: TK83
文献标识码: A
文章编号: 2096-8299(2020)02-0136-05
|
摘要
风机轴承振动信号中混杂着噪声, 会对后期的故障诊断造成困难。提出了一种改进经验模态分解(EMD)与小波阈值降噪相结合的风机数据降噪方法。首先, 采用EMD对原始振动信号进行分解得到信号的固有模态函数, 考虑到各个分量中都含有噪声和信号从而出现模态混叠现象, 故采用相关系数法筛选出信号分量和噪声分量对EMD进行改进。然后, 采用小波阈值法对噪声分量进行降噪, 并将信号分量与处理后的噪声分量进行重构, 最终完成信号降噪。最后, 选取某风机轴承振动数据作为实验数据, 有效地去除了原始信号中的噪声, 并得出轴承内圈故障的结论, 与实际结果一致, 验证了所提方法的有效性。
关键词
经验模态分解; 风机信号; 小波阈值
Abstract
A new noise elimination method is improved to solve the problem of fault diagnosis due to the noise mixed in the vibration signal of wind turbine bearing.Firstly, the original signal is decomposed by empirical mode to get the components of each mode function.Because the noise and signal exist at the same time, the modal overlap will occur, the correlation coefficient is used to screen out the signal component and noise component; then wavelet threshold is used to reduce noise; finally the signal component and the processed noise component are reconstructed to reduce the noise and diagnose the fault.The simulation results show its effectiveness.
Key words
empirical mode decomposition; wind turbine signal; wavelet threshold
风电机组采集系统采集到的信号通常都是将有用信号和噪声混杂在一起, 特别是在故障刚刚发生或故障程度较弱的情况下, 噪声的干扰会很严重, 就增大了故障诊断难度[1-2]。另外, 由于一些人为因素, 加速度传感器中的电路会产生波动信号, 对随后的信号分析结果产生不同程度的影响[3]。风机轴承的振动信号是非线性微弱信号, 易受到噪声的干扰, 其故障特征的提取有一定的困难[4]。
常用的信号处理方法主要有Fourier变换、小波阈值法、频谱分析法、人工神经网络法等[5]。但Fourier变换无法获得信号的全局化结果, 只对平稳的信号比较有效; 小波阈值法虽然可以分离不同频率区间的信号, 但小波基与小波系数的选择较为困难[6-7]。
为了能够更加有效地消除信号中的噪声, 本文提出利用改进经验模态分解(Empirical Mode Decomposition, EMD)与小波降噪相结合的方法, 对风机轴承的振动信号进行降噪。首先, 运用EMD算法对初始信号进行一次降噪处理, 获得分解后的固有模态函数(Intrinsic Mode Function, IMF)分量, 并计算其与初始信号的互相关系数; 然后, 根据相关系数的大小选择出噪声分量, 并用小波阈值法对噪声分量进一步降噪; 最后, 将处理后的信号进行重构得到消噪信号, 从而有效消除原始信号中的噪声。
1 EMD算法与小波阈值法原理
1.1 EMD算法
EMD信号处理算法并不像其他算法一样有设定的基函数, 其全部的分解过程中没有预先设定好的基函数, 信号本身就是所有基函数的来源[7]。EMD会将信号中分布在不同尺度上的波动和趋势离散开, 最终形成若干个IMF分量和一个余项之和[8]。
其中, 每个IMF分量必须全都满足如下两个基本要求:
(1) 所有数值序列中, 全部极值点的数量与全部过零点的数量必须相同或至多两者之间相差1;
(2) 在任意一点上, 所取得的信号包络最大极值与最小极值均值必须为零。
EMD算法具体步骤如下。
步骤1确定原始信号S1(t)全部的局部极大值点和极小值点, 然后用3次样条插值函数确定其上下包络线u1(t)和v1(t), 并计算上下包络线的平均值曲线为
| $ m_{1}(t)=\frac{u_{1}(t)+v_{1}(t)}{2} $ | (1) |
原始信号与包络均值的差值为
| $h_{1}(t)=S_{1}(t)-m_{1}(t)$ | (2) |
如果h1(t)无法达到IMF分量的两个要求, 则将h1(t)看作原初始信号, 不断循环重复上述做法得到h11, h12, h13, …, h1k。
| $h_{1 k}(t)=h_{1}(t)-m_{1 k}(t)$ | (3) |
筛选k次, 直到h1k(t)变为IMF分量, 称为1阶IMF分量, 记为
| $c_{1}(t)=h_{1 k}(t)$ | (4) |
步骤2从初始信号中减去c1(t), 获得1阶剩余信号r1(t)。由于r1(t)中仍包含较长周期的初始信号分量, 因此要对r1(t)进行相同的步骤, 依次得到2阶IMF分量和2阶剩余信号, ……, n阶IMF分量和n阶剩余信号。这一过程可表示为
| $ \left\{\begin{array}{c} r_{1}(t)-c_{2}(t)=r_{2}(t) \\ \vdots \\ r_{n-1}(t)-c_{n}(t)=r_{n}(t) \end{array}\right. $ | (5) |
当rn(t)变成为单调函数时, 筛选结束, 得到
| $ S_{1}(t)=\sum\limits_{i = 1}^n c_{i}(t)+r_{n}(t) $ | (6) |
式(6)表示原始信号被分解为若干个固有模态函数分量与一个余项之和。
1.2 小波阈值法去噪
小波阈值法的本质是对信号进行滤波[9-10]。首先, 为了得到初始信号的小波分解系数, 对初始信号进行一次小波变换; 然后, 根据小波系数能够反映出信号性质的特性, 对其进行阈值运算, 经过阈值处理后便可以过滤掉信号中存在的噪声; 最后, 用小波逆变换方法将小波系数进行逆变换处理, 即重新构造小波, 便完成了对信号的降噪。
小波阈值可以由Stein无偏风险估计原理得到。软阈值法降噪后信号会失真, 硬阈值法降噪后信号不连续, 重构信号会发生振荡。半软阈值函数减小了软阈值法带来的偏差, 同时兼顾了硬阈值法的优点, 弥补了两种方法存在的不足。因此, 本文选择半软阈值法对小波系数进行处理, 小波分解层数为4, 小波分解基函数为db8。半软阈值函数为
| $W_{\tau}=\left\{\begin{array}{ll}\operatorname{Sign}(W)\left[|W|-\frac{T}{\mathrm{e}^{m\left(W^{2}-T^{2}\right)}}\right] & |W| \geqslant T \\ 0 & |W|<T\end{array}\right.$ | (7) |
式中:Wτ——经过域值处理后的小波系数;
W——信号分解后的小波系数值;
T——阈值;
m——调节因子。
2 改进的EMD-小波阈值法
为了弥补EMD方法中存在的缺陷, 本文使用相关系数法来解决EMD所产生的信号模态相互混叠的问题。其原理为:噪声主导分量与振动信号之间的相关度小, 而信号主导分量与振动信号之间的相关度大, 求得各IMF与初始信号之间的相关系数, 并将其与设定值进行比较, 来筛选和判断该分量是噪声分量还是信号分量。利用小波阈值法对噪声分量进行二次降噪, 最后将二次降噪的噪声分量与信号分量进行重构便得到最终的降噪信号。改进算法的具体流程如图 1所示。
(1) 设含噪信号为S(t), 对S(t)首先进行EMD, 获得各个IMF分量和一个剩余分量。
(2) 依次计算出每个IMF分量与原初始信号间的相关系数, 公式为
| $ \rho_{x y}=\frac{\sum\limits_{n = 0}^\infty x(n) y(n)}{\sqrt{\sum\limits_{n=0}^{\infty} x^{2}(n) \sum\limits_{n = 0}^\infty y^{2}(n)}} $ | (8) |
式中:x(n), y(n)——时间序列。
(3) 依据经验, 设定阈值为最大相关系数的1/10, 并以此对各IMF进行筛选, 将筛选出的噪声分量进行下一步小波阈值降噪。
(4) 将经过小波降噪后的IMF分量与信号主导IMF分量进行信号重构, 得到最终的降噪信号S′(t)。
3 风机振动数据降噪和故障诊断
3.1 风机轴承振动数据的降噪
实验数据选取某海上风机的振动数据, 轴承型号为FL-HSN2410DFT1, 内圈随工作轴转动, 转动速度为800 r/min, 传感器的采样频率为12 000 Hz。通过计算得出轴承的故障频率分别为:外圈105.43 Hz, 内圈156.68 Hz, 滚动体133.49 Hz。图 2为某时刻原始信号的波形和频谱。
由图 2可以看出, 原始信号波形有微弱的周期性冲击信号, 频率分布不集中, 初步判定轴承运行在故障状态, 对其进行EMD-小波阈值降噪处理。首先对其进行EMD, 得到13个IMF分量和一个剩余分量r, 如图 3所示。限于篇幅, 文中只给出前6个。
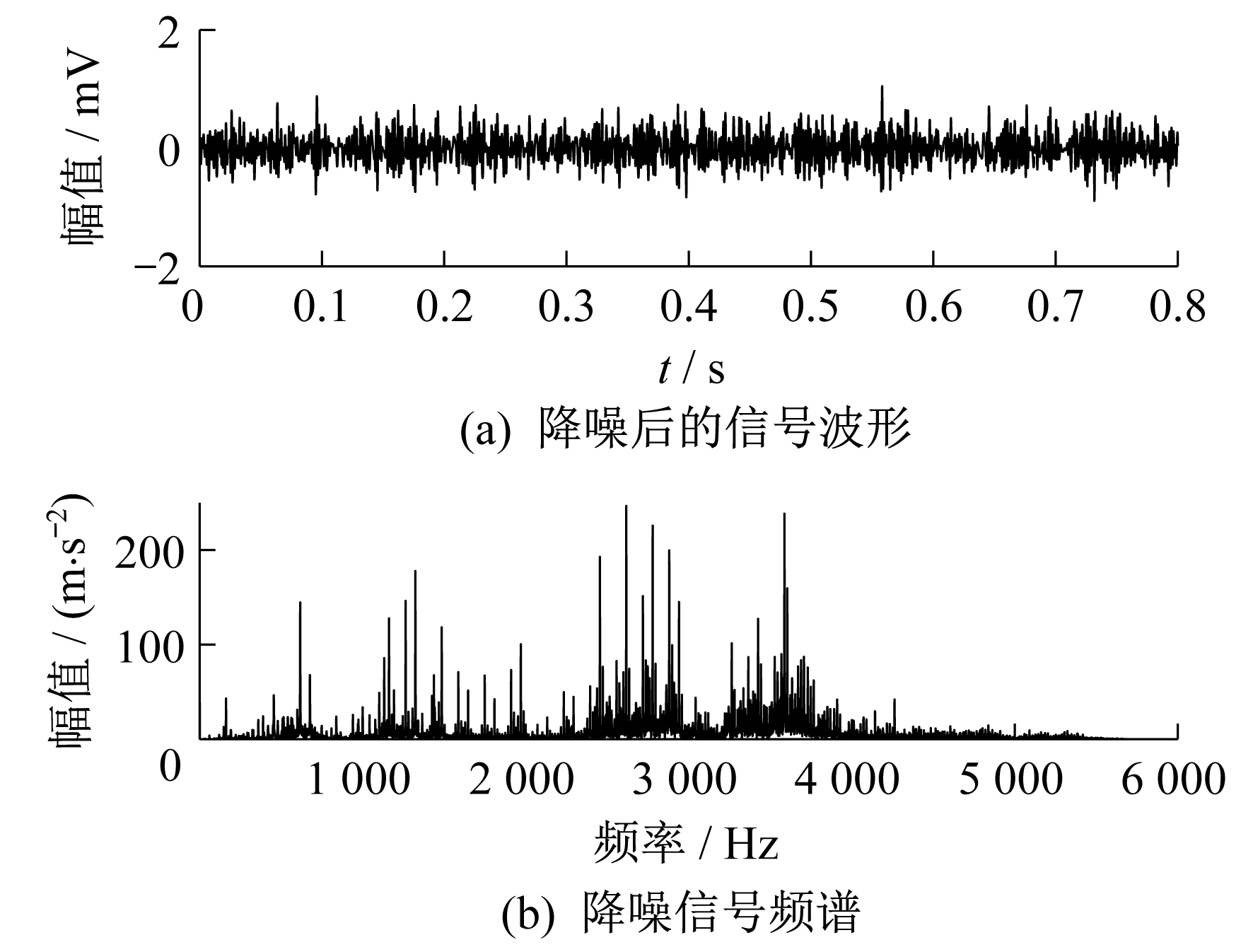
采用相关系数法对噪声分量和信号分量进行进一步筛选, 依据式(8)求出各个IMF分量与初始信号之间的相关系数, 如表 1所示。将相关系数的大小与设定值相比较, 选出相关性最大的几个分量。将IMF4~IMF10作为信号分量, 剩余的IMF分量作为噪声分量并对其进行小波阈值降噪, 则重构信号=信号分量+噪声分量, 其波形和频谱如图 4所示。
表 1
各IMF分量与原始信号的相关系数
| IMF | 相关系数 | IMF | 相关系数 |
| 1 | 0.015 | 8 | 0.254 |
| 2 | 0.026 | 9 | 0.163 |
| 3 | 0.039 | 10 | 0.081 |
| 4 | 0.362 | 11 | 0.006 |
| 5 | 0.463 | 12 | 0.012 |
| 6 | 0.656 | 13 | 0.001 |
| 7 | 0.523 |
一般信号和噪声信号的区别在于:噪声信号只在零点处取得函数最大值1, 在其他点处函数值会快速降到较小值; 一般信号之间都会存在一定的关联性, 其自相关系数也会在零时刻获得最大值, 但其他点的自相关函数值并不会很快降到极小值, 而是随着信号的变化而变化。
因此, 可利用噪声信号与一般信号自相关性的差异来验证本文方法的有效性。将原始信号减去降噪后的信号得到两者的差值信号, 如图 5所示。将上述差值信号进行自相关性分析, 结果如图 6所示。
由图 6可以看出, 差值信号自相关函数在零点处取得了最大值, 并且在其余点处的函数值都很小, 符合噪声信号的基本特征, 从侧面反映了本文提出的方法具有良好的降噪效果。
分别计算本文方法与传统EMD方法的信噪比(SNR)和均方误差(MSE)。用EMD方法对振动信号进行降噪后, SNR为20.81 dB, MSE为0.46 dB; 采用改进EMD -小波阈值法处理后, SNR提高到21.27 dB, MSE降低到0.35 dB。两项性能指标都得到了改善, 说明了本文所提出方法的可行性。
3.2 轴承的故障诊断
4 结语
风机振动信号中存在着大量噪声, 对其后进行精确故障诊断造成了一定的困难。本文提出了改进的EMD-小波阈值降噪方法。利用EMD对初始信号进行分解, 并用小波阈值法对筛选出的噪声分量进一步降噪, 将处理后的信号进行重构得到消噪信号。实验表明:该方法能够有效地去除噪声, 提高信噪比和降低均方误差, 为后期进行精确的故障诊断作好准备, 是一种有效可行的信号降噪方法。
参考文献
-
[1]大功率并网风电机组状态监测与故障诊断研究综述[J]. 电力自动化设备, 2016, 36(1): 6-16.
-
[2]基于EMD的改进马田系统的滚动轴承故障诊断[J]. 振动与冲击, 2017, 36(5): 151-156.
-
[3]滚动轴承复合故障诊断的自适应方法研究[J]. 振动与冲击, 2016, 35(10): 145-150.
-
[4]基于单通道盲源分离的齿轮故障诊断研究[J]. 现代制造工程, 2017(4): 138-141.
-
[5]分层自适应小波阈值轴承故障信号降噪方法[J]. 振动工程学报, 2019, 32(3): 548-556.
-
[6]EEMD降噪与倒频谱分析在风电轴承故障诊断中的应用[J]. 机床与液压, 2018, 46(13): 156-159. DOI:10.3969/j.issn.1001-3881.2018.13.038
-
[7]基于小波包分解的电力系统谐波检测分析[J]. 上海电力学院学报, 2017, 33(1): 60-64.
-
[8]WANG C Q, ZHOU J Z, QIN H, et al. Fault diagnosis based on pulse coupled neural network and probability neural network[J]. Expert Systems with Applications, 2011, 38(11): 14307-14313.
-
[9]EMD去噪法在FMCW雷达信号处理中的应用[J]. 科学技术与工程, 2014, 14(27): 66-70. DOI:10.3969/j.issn.1671-1815.2014.27.013
-
[10]基于改进阈值函数的小波阈值去噪算法[J]. 计算机系统应用, 2016, 25(6): 191-195.