|
|
|
发布时间: 2020-04-10 |
|
|
|
|
收稿日期: 2019-10-07
基金项目: 上海市青年科技英才扬帆计划(16YF1404700)
中图法分类号: TK39
文献标识码: A
文章编号: 2096-8299(2020)02-0161-07
|
摘要
火电厂选择性催化还原法(SCR)烟气脱硝系统是处理燃煤机组烟气排放NOx污染的主要途径, 但该系统具有多输入变量、环境影响复杂、时变非线性等特征, 因此建立准确的系统模型是SCR优化控制的基础。提出了一种融合遗传算法(GA)主元分析和广义回归神经网络(GRNN)数据挖掘的SCR系统建模方法。首先使用GA对运行数据进行变量选择优化计算; 然后将最优变量作为GRNN的输入量, 利用数据挖掘技术建立SCR系统数据模型。基于某电厂机组运行数据的实例分析表明, 该方法建立的模型具有复杂度低、精度高、泛化能力强等优点。
关键词
选择性催化还原法; NOx排放; 遗传算法; 广义回归神经网络; 数据模型
Abstract
The selective catalytic reduction (SCR) flue gas denitration system is the main way to deal with the pollution of NOx discharged from coal-fired units.The system has characteristics such as multiple input variables, complex environmental impact, and time-varying nonlinearity.Therefore, establishing an accurate system model is the basis of SCR system optimization control.A method to establish SCR system model based on genetic algorithm(GA) principal component analysis and generalized regression neural network(GRNN) data mining is proposed.Firstly, GA is used to optimize the calculation of variable selection.Then the optimal variable is used as the input of GRNN.The data model of SCR system is established by data mining.The example verification based on the running data of a power plant unit shows that the model established by this method has the advantages of low complexity, high precision and strong generalization ability.
Key words
selective catalytic reduction; NOx emission; genetic algorithm; generalized regression neural network; data model
近年来, 随着我国经济的发展, 能源消费中所带来的环境污染也越来越严重。氮氧化物(NOx)是主要的大气污染物之一, 伴随着耗电量的增加, 燃煤电厂的烟气浓度排放成为重点关注对象[1-4]。我国对氮氧化物排放控制标准的要求越来越严格, 为了控制火电厂尾气中氮氧化物的排放, 燃煤电厂广泛使用选择性催化还原法(Selective Catalytic Reduction, SCR)烟气脱硝系统, 因此各电厂对SCR系统优化控制技术的需求十分迫切[5]。准确的模型是系统优化控制的基础, 选择合适的输入变量是建立模型的重要前提。
随着人工智能技术的迅速发展, 数据建模方法得到了广泛研究[6]。周洪煜等人[7]采用径向基函数神经网络建立了SCR脱硝系统模型并优化出口烟气NH3/NOx比值; MEHMOOD T等人[8]对常用的变量选择方法进行了详细论述; 徐富强等人[9]建立了最优径向基函数模型, 通过平均影响值算法来进行变量处理。刘吉臻等人[10]采用点互信息进行了变量选择并建立了脱硝系统模型。
本文采用遗传算法(Genetic Algorithm, GA)对SCR系统运行数据进行优化计算, 经过主元分析选出重要的独立变量; 然后将变量选择结果作为广义回归神经网络(Generalized Regression Neural Network, GRNN)模型输入变量, 通过交叉验证的方法训练GRNN, 利用数据挖掘技术建立SCR系统的GRNN优化控制数据模型; 最后基于上海华能某电厂机组SCR系统运行数据进行了验证。
结果表明, 该方法建立的模型具有拟合度高、复杂度低、泛化能力强等优点, 能准确反映SCR系统的变化过程, 在电厂SCR系统升级建设中具有较高的实用价值。
1 SCR烟气脱硝系统介绍
图 1为上海华能某电厂燃煤机组采用的SCR烟气脱硝系统。
SCR脱硝装置布局在锅炉省煤器和空气预热器的中间, 设计为高灰型, 安装上SCR反应器, 烟气挡板分别装在反应器两侧进口烟道以及省煤器旁路。SCR脱硝系统采用TiO2作为催化剂, 用尿素制备脱硝还原剂。热解炉中的氨气还原剂由热解喷枪喷出尿素溶液蒸发而来, 空气/氨气混合物通过热解炉出口的母管分散进入各分支管, 混合气体通过分支管的喷氨栅格进入烟道, 静态混合器将烟气与氨气进行充分混合后送入催化反应器。催化氧化还原反应在氨气与NOx达到相应温度时开始发生, 这样NOx就被还原为N2和H2O, 以实现烟气脱硝[11]。其脱硝效率受氨氮比、烟气含氧量、锅炉温度、进风量、反应时间等一系列因素的影响[12]。
SCR脱硝过程发生的主要化学反应如下:
| $4 \mathrm{NO}+4 \mathrm{NH}_{3}+\mathrm{O}_{2} \rightarrow 4 \mathrm{N}_{2}+6 \mathrm{H}_{2} \mathrm{O}$ | (1) |
| $\mathrm{NO}+\mathrm{NO}_{2}+2 \mathrm{NH}_{3} \rightarrow 2 \mathrm{N}_{2}+3 \mathrm{H}_{2} \mathrm{O}$ | (2) |
| $6 \mathrm{NO}_{2}+8 \mathrm{NH}_{3} \rightarrow 7 \mathrm{N}_{2}+12 \mathrm{H}_{2} \mathrm{O}$ | (3) |
| $4 \mathrm{NH}_{3}+3 \mathrm{O}_{2} \rightarrow 2 \mathrm{N}_{2}+6 \mathrm{H}_{2} \mathrm{O}$ | (4) |
| $4 \mathrm{NH}_{3}+5 \mathrm{O}_{2} \rightarrow 4 \mathrm{NO}+6 \mathrm{H}_{2} \mathrm{O}$ | (5) |
2 基于GA-GRNN数据挖掘的SCR系统模型
2.1 SCR系统模型优化分析
在SCR系统数据建模时, 既要考虑全工况, 又要考虑各种影响因素。发电机组动态工况下各变量特性不稳定, 模型的准确度与其息息相关。其中, 关联度最大的有机组负荷、入口烟气NOx含量、入口烟气温度、入口烟气含氧量、喷氨量、SCR反应器1层压力差、SCR反应器2层压力差、SCR反应器3层压力差、进入反应器前总压力、总煤量、总风量、出口烟气含氧量共12个变量。系统输出为烟囱入口NOx含量。在建立系统数据模型时, 加入过多关联性小的输入变量会加剧模型建立的复杂度, 因此对变量影响因素进行主元分析, 选择出重要的独立变量是提高模型精度的重要环节。12个输入变量及序号如表 1所示。
表 1
12个变量及序号
| 序号 | 变量名 |
| 1 | 机组负荷 |
| 2 | 入口烟气NOx含量 |
| 3 | 入口烟气温度 |
| 4 | 入口烟气含氧量 |
| 5 | 喷氨量 |
| 6 | SCR反应器1层压力差 |
| 7 | SCR反应器2层压力差 |
| 8 | SCR反应器3层压力差 |
| 9 | 进入反应器前总压力 |
| 10 | 总煤量 |
| 11 | 总风量 |
| 12 | 出口烟气含氧量 |
其中, 机组负荷与烟囱入口烟气NOx含量变化关系如图 2所示。
由图 2可知, 在机组负荷上升时, 烟囱出口烟气NOx含量也随之升高, 即喷氨调节的延迟会造成排放超标, 喷氨量加大。为了达到排放标准, 电厂会进行过量喷氨, 导致氨逃逸的发生。因此, 通过数据挖掘技术建立准确的SCR数据优化模型是电厂改造形势所需。
2.2 GA变量选择方法
GA最初由美国的HOLLAND J教授提出, 它通过模拟种群自然选择和基因遗传中发生的复制、交叉和变异等现象, 通过选择、交叉和变异进而得到最适应此环境的个体, 从而能够求得变量选择最优解[13]。
所需的N个初始串结构数据系统随机产生, 一个串结构数据对应一个种群个体, 分为0/1两个值。适应度是GA用来度量群体中每个个体在优化计算中达到最优解的程度, X为相应个体, 用适应度函数来度量每个个体适应度的大小。本文取测试数据误差平方和的倒数为适应度函数, 即
| $ f(X)=\frac{1}{\operatorname{sse}(\hat{T}-T)}=\frac{1}{\sum\limits_{i=1}^{n}\left(\hat{t}_{i}-t_{i}\right)^{2}} $ | (6) |
式中:
 测试集预测值,
测试集预测值,

T——测试集的真实值, T={t1, t2, t3, …, tn};
n——测试集的数目。
选择操作选用比例选择算子, 代表被选中的个体能遗传到下一代种群的概率与该个体适应度大小成正比。
计算种群中所有个体的适应度值之和
| $ F=\sum\limits_{k=1}^{n_{r}} f\left(X_{k}\right) $ | (7) |
式中:nr——个体特征总数;
k——个体特征;
Xk——种群中的各个个体。
计算每个个体的相对适应度, 并将其作为该个体被选中然后能遗传到下一代种群的概率, 即
| $ p_{k}=\frac{f\left(X_{k}\right)}{F} \quad k=1,2,3, \cdots, n_{\mathrm{r}} $ | (8) |
式中:F——种群中所有个体的适应度之和。
用模拟轮盘赌操作, 产生0~1之间的随机数, 确定个体被选中的次数。个体的适应度越大, 被选中的概率也就越大, 其基因也就会在种群中逐渐扩大。
交叉操作采用单点交叉算子。先进行种群中个体的两两随机配对, 然后选出配对个体的基因交叉点, 再交换两个个体的部分染色体, 产生两个新个体, 其原理如图 3所示。
变异操作采用单点交叉算子。先随机产生变异点, 然后改变对应基因座上的基因值, 其原理如图 4所示。
经过不断的迭代操作后, 当达到迭代截止条件时, 得到的末代种群即为筛选出的重要输入变量。
2.3 GRNN算法
GRNN是美国学者SPECHT D F提出的一种径向基神经网络。其优点是非线性映射能力强、柔性网络结构以及超高的容错性和鲁棒性, 多用于解决非线性问题。
GRNN网络结构由输入层、模式层、求和层和输出层4层构成, 如图 5所示[14]。
GRNN的理论基础是非线性回归分析, 通过计算含有最大概率值的y来进行非独立变量Y于独立变量x的回归分析。设f(x, y)表示随机变量x和y的联合概率密度函数, 已知x的观测值为X, y是相对于X的回归, 条件均值为
| $ \hat{Y}=E\left(\frac{y}{X}\right)=\frac{\int_{-\infty}^{\infty} y f(X, y) \mathrm{d} y}{\int_{-\infty}^{\infty} f(X, y) \mathrm{d} y} $ | (9) |
式中:
 在输入X条件下Y的预测输出。
在输入X条件下Y的预测输出。
通过Parzen非参数估计, 利用样本数据集 估算出密度函数
估算出密度函数
| $ \begin{aligned} \hat{f}(X, y)=& \frac{1}{n(2 \pi)^{\frac{p+1}{2}} \sigma^{p+1}} \sum_{i=1}^{n} \exp \left[-\frac{\left(X-X_{i}\right)^{\mathrm{T}}\left(X-X_{i}\right)}{2 \sigma^{2}}\right] \times \\ & \exp \left[-\frac{\left(X-Y_{i}\right)^{2}}{2 \sigma^{2}}\right] \end{aligned} $ | (10) |
式中:p——随机变量x的维数;
σ——Gaussian函数的密度系数;
Xi, Yi——随机变量x和y的观测值。
利用 替换f(X, y)并代入式(10)中, 得
替换f(X, y)并代入式(10)中, 得
| $ \begin{aligned} \hat{Y}(X)=& \sum_{i=1}^{n} \exp \left[-\frac{\left(X-X_{i}\right)^{\mathrm{T}}\left(X-X_{i}\right)}{2 \sigma^{2}}\right] \centerdot \\ & \int_{-\infty}^{+\infty} y \exp \left[-\frac{\left(X-Y_{i}\right)^{2}}{2 \sigma^{2}}\right] \mathrm{d} y \times \\ & \left(\sum_{i=1}^{n} \exp \left[-\frac{\left(X-X_{i}\right)^{\mathrm{T}}\left(X-X_{i}\right)}{2 \sigma^{2}}\right] \centerdot\right.\\ & \left.\int_{-\infty}^{+\infty} \exp \left[-\frac{\left(Y-Y_{i}\right)^{2}}{2 \sigma^{2}}\right] \mathrm{d} y\right)^{-1} \end{aligned} $ | (11) |
由于 ze-z2dz=0, 故可通过积分计算得出网络输出
ze-z2dz=0, 故可通过积分计算得出网络输出 为
为
| $ \hat{Y}(X)=\frac{\sum\limits_{i=1}^{n} Y_{i} e x p\left[-\frac{\left(X-X_{i}\right)^{T}\left(X-X_{i}\right)}{2 \sigma^{2}}\right]}{\sum\limits_{i=1}^{n} \exp \left[-\frac{\left(X-X_{i}\right)^{T}\left(X-X_{i}\right)}{2 \sigma^{2}}\right]} $ | (12) |
估计值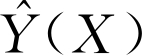 是观测值Yi的全部加权平均数, 所有Yi的权重因子是其样本Xi与X两者Euclid距离平方的指数。当σ取合适值时, 便能考虑所有训练数据的因变量, 加大与预测点最近的样本点所对应因变量的权值。
是观测值Yi的全部加权平均数, 所有Yi的权重因子是其样本Xi与X两者Euclid距离平方的指数。当σ取合适值时, 便能考虑所有训练数据的因变量, 加大与预测点最近的样本点所对应因变量的权值。
2.4 基于GA-GRNN数据挖掘的SCR系统模型
数据挖掘技术是一种数据库知识的发现, 是从采集的海量数据中通过算法搜索隐藏其中的信息和规律的过程, 主要包括三大流程:数据预处理、数据挖掘算法以及知识表示和评估。
首先, GA变量选择是利用GA进行优化计算, 编码长度设计为N, 种群大小为M, 最大进化代数设为X, 染色体每一位对应一个输入变量。每一位基因只能取“0”和“1”两种情况:如果某一位是“1”, 其对应的输入变量参与最后的建模; 若为“0”, 则不参与最后建模。取测试样本集和方差的倒数为遗传算法适应度函数, 选择运算采用比例选择算子, 交叉运算采用单点交叉算子, 变异运算采用单点变异算子, 经过大量数据的不断迭代进化。当满足迭代终止条件(最大进化代数)时, 筛选出最优变量作为建模的输入变量{w1, w2, w3, …, wi}。
因一般神经网络在函数逼近时存在收敛速度慢和局部极小等一系列缺点, 而GRNN数据挖掘技术在逼近能力、分类能力和学习速度方面具有较强优势, 网络最后收敛于样本量积累最多的优化回归面, 并且可以处理不稳定的数据, 因此将其用于基于数据的系统模型的建立。
以GA筛选出的{w1, w2, w3, …, wi}作为网络输入, 构建GRNN模型, 利用大量数据进行数据挖掘, 采用交叉验证的方法训练GRNN。当SPREAD值(即径向基函数的扩展速度, 默认值为1)较小时, 网络对样本的逼近能力较强; 当SPREAD值越大时, 网络对样本的近似越平滑, 误差也变大。
在建模过程中, 为了得出最佳的SPREAD值, 通常用循环训练法找出最佳值, 并以此最佳方法建立GRNN, 从而达到最好的预测效果。利用GA变量选择优化GRNN建模的流程如图 6所示。
3 算例分析
通过采集华能上海某火电厂1#机组SCR系统的实际运行数据, 来验证本文提出的基于GA-GRNN数据挖掘技术的建模方法的有效性。选取正常运行下1#机组负荷变化较大的某一周, 间隔1 min进行采样, 处理掉异常数据, 选取720组历史运行数据作为研究样本, 其中600组数据作为训练数据, 剩余120组作为测试数据。原始12个输入变量如表 1所示。
先将所有数据样本进行平滑处理, 归一化到[-1, 1]范围内, 利用GA进行变量选择, 编码长度为12, 种群大小为20个, 最大进化代数设为60代, 选取测试样本均方误差倒数为GA适应度函数, 经过数据挖掘不断迭代筛选出最优输入变量[15]。
模型精度评价指标采用均方根误差(Root Mean Square Error, RMSE)和平均绝对百分比误差(Mean Absolute Percentage Error, MAPE), 计算公式为
| $ \mathrm{RMSE}=\sqrt{\frac{\sum\limits_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}}{n}} $ | (13) |
| $ \mathrm{MAPE}=\frac{1}{n} \sum\limits_{i=1}^{n} \left| {\frac{y_{i}-\hat{y}_{i}}{y_{i}}} \right| $ | (14) |
式中:
 测量值和预测值。
测量值和预测值。
GA适应度函数进化曲线如图 7所示。变量选择结果如图 8所示。
筛选出的最优变量结果为“1”, 由图 8得原始变量序号为1, 2, 5, 8, 9, 10, 12, 即为机组负荷、入口烟气NOx含量、喷氨量、SCR反应器3层压力差、进入反应器前总压力、总煤量、出口烟气含氧量。
通过基于GA变量选择得出的7个输入变量以及输出变量烟囱入口烟气NOx含量构建GRNN模型。采用交叉验证方法训练GRNN, 并循环找出最佳SPREAD值, 利用数据挖掘GRNN对SCR脱硝系统进行优化建模, 结果如图 9所示。
运行显示, 最佳SPREAD值为0.1, GRNN模型计算值大致在实际测量值附近, 说明模型能很好地反映SCR脱硝系统出口烟气NOx含量的动态变化, 具有很好的精度以及较强的学习能力和泛化能力。
将本文提出的方法与其他方法进行对比。利用数据挖掘技术, 首先通过原始12个输入变量进行BP神经网络建模, 然后通过GA变量选择得出的7个输入变量进行BP神经网络建模以验证变量选择对模型精度的影响, 并将7个输入变量用于Elman建模与GRNN模型进行比较。其中原变量BP模型计算结果如图 10所示, GA-BP模型计算结果如图 11所示, GA-Elman模型计算结果如图 12所示。不同建模方法下各指标比较如表 2所示。
表 2
不同建模方法比较
| 模型 | $\mathrm{RMSE} /\left(\mathrm{mg} \cdot \mathrm{m}^{-3}\right)$ | $\mathrm{MAPE} / \%$ | 建模时间$/ \mathrm{s}$ |
| $\mathrm{BP}$ | 3.9689 | 10.3649 | 2.62500 |
| $\mathrm{GA}-\mathrm{BP}$ | 3.5873 | 9.7064 | 0.23438 |
| $\mathrm{GA} -\mathrm{Elman}$ | 2.8148 | 6.9653 | 0.14063 |
| $\mathrm{GA}-\mathrm{GRNN}$ | 2.0224 | 4.5687 | 0.12500 |
通过图 9~图 12和表 2可以发现, BP神经网络泛化能力最差; 利用GA-BP, GA-GRNN, GA-Elman模型与BP模型进行对比发现, 变量选择能提高模型精度, 降低模型复杂度, 证明GA变量选择算法在该系统中的适应性; 通过对比GA-BP, GA-GRNN, GA-Elman 3种模型发现, GRNN的拟合效果最好, 测试样本计算结果误差最小, MAPE只有4.568 7%, 模型精度大幅提高, 建模时间缩短, 说明GRNN算法提高了模型的准确性和鲁棒性, 能够满足工程优化需要。
4 结语
本文采用数据挖掘技术, 通过GA优化计算进行变量选择, 在连续迭代演化后, 筛选出最具代表性的输入自变量参与建模。然后将最优输入变量作为GRNN的输入, 采用交叉验证方法训练GRNN, 通过循环找到最佳SPREAD, 最终建立SCR脱硝系统数据模型。实例分析表明, 通过GA变量选择减少输入变量的数量可以有效地降低模型的难度和复杂性, 建立的GRNN模型具有模型泛化能力强、精度高等优点, 能够进一步实现SCR脱硝系统优化控制以及智能电厂的建设与改造。
参考文献
-
[1]300 MW级燃煤电站锅炉烟气低温脱硝及脱汞试验研究[J]. 上海电力学院学报, 2018, 34(4): 329-332.
-
[2]基于我国新大气污染排放标准下的燃煤锅炉高效低NOx协调优化系统研究及工程应用[J]. 中国电机工程学报, 2014, 34(增刊1): 122-129.
-
[3]火电厂氮氧化物排放控制技术[J]. 环境工程, 2008, 26(6): 82-85.
-
[4]选择性催化还原烟气脱硝技术在玉环电厂4×1 000 MW机组上的应用[J]. 电力环境保护, 2009, 25(3): 1-3.
-
[5]核心向量机的电站锅炉NOx排放特性大数据建模[J]. 中国电机工程学报, 2016, 36(3): 717-722.
-
[6]电站锅炉SCR烟气脱硝系统优化数值模拟[J]. 动力工程学报, 2014, 34(1): 50-56.
-
[7]超临界锅炉烟气脱硝喷氨量混结构-径向基函数神经网络最优控制[J]. 中国电机工程学报, 2011, 31(5): 108-113.
-
[8]MEHMOOD T, LILAND K H, SNIPEN L, et al. A review of variable selection methods in partial least squares regression[J]. Chemometrics and Intelligent Laboratory Systems, 2012, 118(2): 62-69.
-
[9]基于优化的RBF神经网络的变量筛选方法[J]. 计算机系统应用, 2012, 21(3): 206-208. DOI:10.3969/j.issn.1003-3254.2012.03.047
-
[10]基于偏互信息的变量选择方法及其在火电厂SCR系统建模中的应用[J]. 中国电机工程学报, 2016, 36(9): 2438-2443.
-
[11]脱硝技术的现状及展望[J]. 洁净煤技术, 2017, 23(2): 12-19.
-
[12]燃煤电站尿素热解SCR脱硝优化系统[J]. 锅炉技术, 2018, 49(4): 6-11. DOI:10.3969/j.issn.1672-4763.2018.04.002
-
[13]基于多种群遗传算法的含分布式电源的配电网故障区段定位算法[J]. 电力系统保护与控制, 2016, 44(2): 36-41. DOI:10.7667/j.issn.1674-3415.2016.02.005
-
[14]基于广义回归网络的动态权重回归型神经网络集成方法研究[J]. 计算机应用研究, 2005(12): 47-49. DOI:10.3969/j.issn.1001-3695.2005.12.015
-
[15]电站空冷系统变工况性能的数值研究[J]. 中国电机工程学报, 2012, 32(35): 66-73.


















