|
|
|
发布时间: 2020-04-10 |
|
|
|
|
收稿日期: 2019-11-21
中图法分类号: TM461.5
文献标识码: A
文章编号: 2096-8299(2020)02-0173-06
|
摘要
提出了一种适用于数字化控制的双向CLLC变换器同步整流策略。采用差分比较电路、高频变压器和高速比较器, 将主回路电压电流信号转换为数字信号, 输入现场可编程逻辑门阵列, 完成同步整流控制。实验结果表明, 该方法简单有效, 最多可以提高变换器5%的转换效率。
关键词
CLLC变换器; 数字化控制; 现场可编程逻辑门阵列; 同步整流
Abstract
This paper proposes a synchronous rectification strategy for bidirectional CLLC converters suitable for digital control, using differential comparison circuit, high frequency transformer and high speed comparator to convert the main loop voltage and current signals into digital signal.The field programmable gate array is input to complete the synchronous rectification control.The experiment proves that the method is simple and effective, which can increase the conversion efficiency of the converter by up to 5%.
Key words
CLLC converter; digital control; field programmable gate array(FPGA); synchronous rectification
随着电动汽车、可再生能源、储能系统、不间断电源系统及电力电子变压器等领域的快速发展, 具备能量双向流动的双端口隔离型双向直流-直流(Direct Current-Direct Current, DC-DC)变换器得到了广泛应用, 并成为了研究热点[1-5]。能否实现高功率密度和高变换效率一直是DC-DC变换器设计的重点和难点。目前大量学者致力于具备软开关能力的DC-DC变换器研究, 以减少损耗、提高效率。近些年来, 软开关谐振型DC-DC变换器拓扑以及LLC谐振变换器参数优化得到了越来越多的关注[6-10]。然而, LLC谐振变换器一般只工作于单相传递能量的情况, 反向工作时, 为LC震荡, 调频范围过宽, 负载调节率受限。目前也有文献对LLC谐振变换器在双向DC-DC变换器中的应用进行了研究。如文献[11]提出了对称结构的CLLC谐振变换器, 但其谐振点的增益小于1且受负载影响。为了提高效率, DC-DC变换器一般会采用同步整流的方法。文献[12]提出了一种基于无传感器的LLC电路输出侧同步整流策略, 虽然减少了传感器, 但是该方法仅适用于LLC电路。文献[13]提出了采用专用芯片进行同步整流, 减小了外围电路设计, 适合于能量单相传递情况, 难以与双向CLLC变换器兼容。
本文提出了一种适用于全数字化控制的双向CLLC变换器同步整流策略, 并且通过实验证明, 该方法简单有效, 最多可以提高变换器5%的转换效率。
1 CLLC电路损耗分析
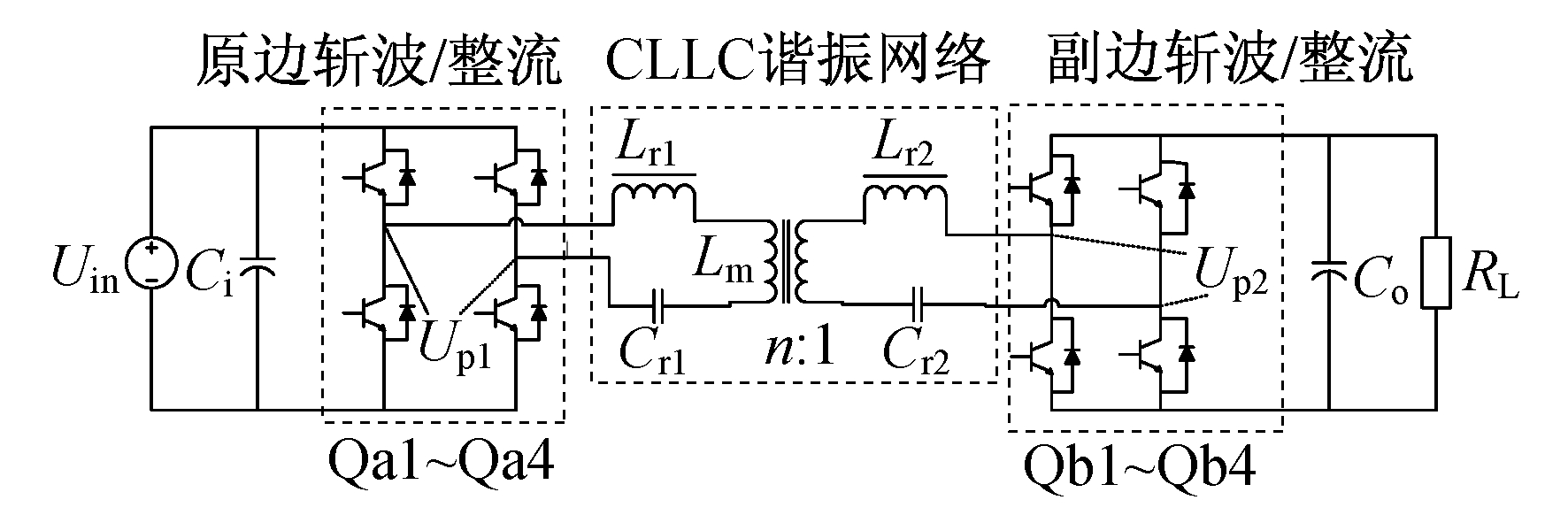
全桥CLLC变换器的拓扑结构如图 1所示。
在正向工作时, 电路一次侧的Qa1~Qa4斩波, 将输入电压Uin转化为高频方波电压Up1, Up1通过CLLC网络, 传递到电路二次侧, 即高频交流电压Up2, 经过Qb1~Qb4的反并联二极管整流, 电容Co滤波, 成为给负载供电的稳定直流。此时Qb1~Qb4关闭, 仅通过体二极管进行整流。由于电路拓扑完全对称, 反向工作时与正向相类似。当变压器变比n≫1时, 电路正反向工作差异较大, 而CLLC电路一般工作于双边电压相差不大的情况下, 故变压器变比n一般取1。
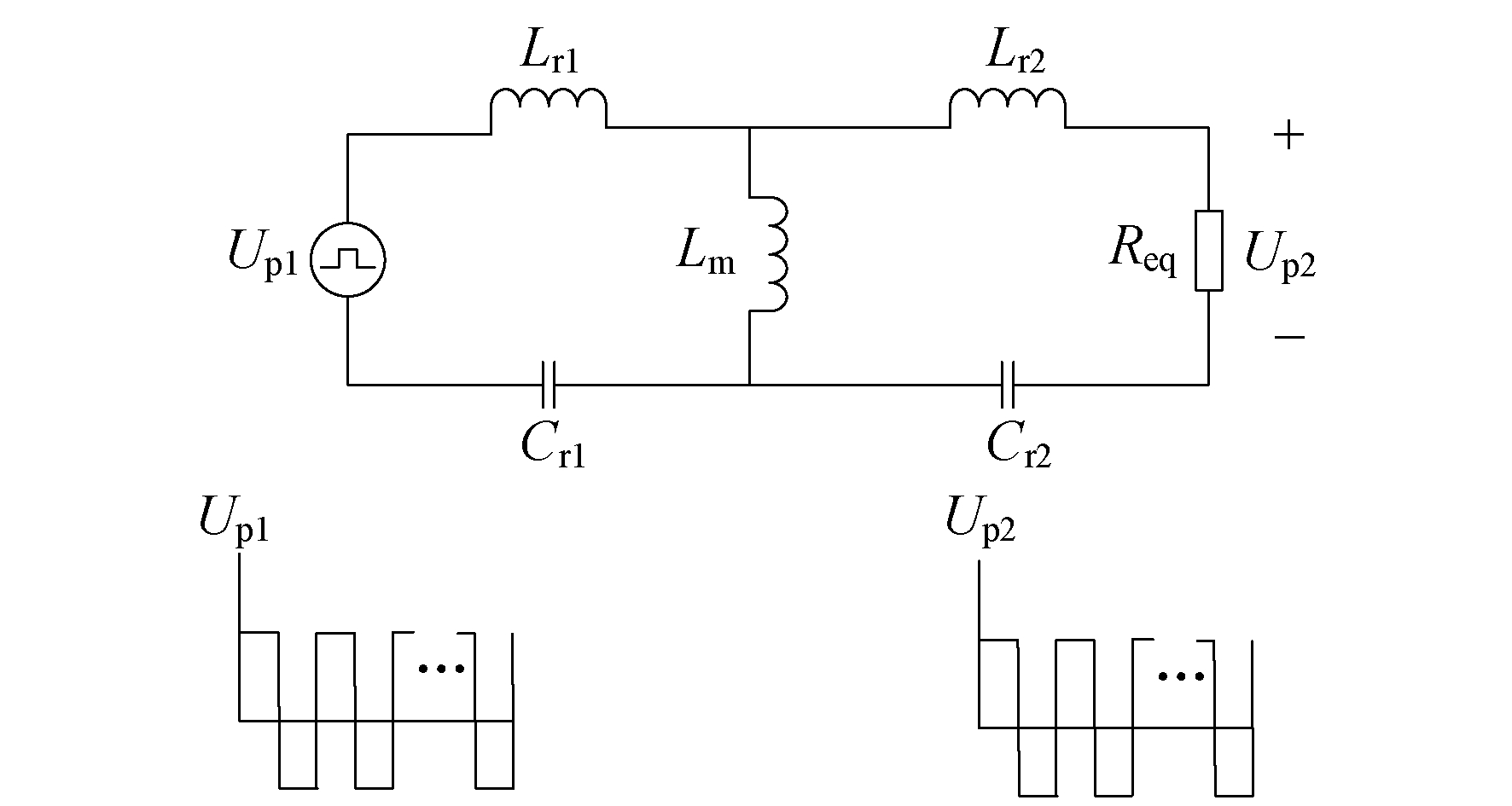
由于CLLC电路中非线性器件较多, 直接采用时域分析或者模态分析过于复杂, 因此先采用基波分析法对CLLC电路进行简化, 简化后的电路如图 2所示。
考虑到实际工程中谐振电感Lr1和Lr2的设计比较复杂, 对其初始磁导率μ和线径等参数有严格的要求。因此, 为了简化理论分析, 也为了降低成本, 令Lr=Lr1=Lr2, Cr=Cr1=Cr2, 此时CLLC谐振腔为互易二端口网络。
在图 2中, 令输入交流电压基波幅值为Uin, 其向量表示形式为Uin, 频率为fc, 角频率ωc=2πfc, 相角为0 rad/s, 可得等效交流开路输出电压
| $ \dot{\boldsymbol{U}}_{\mathrm{eq}}=\frac{\mathrm{j} L_{\mathrm{m}} \omega_{\mathrm{c}}}{-\frac{\mathrm{j}}{C_{\mathrm{r}} \omega_{\mathrm{c}}}+\mathrm{j} L_{\mathrm{m}} \omega_{\mathrm{c}}+\mathrm{j} L_{\mathrm{r}} \omega_{\mathrm{c}}} \boldsymbol{U}_{\mathrm{in}} $ | (1) |
令输出负载电阻为RL, 可得交流负载电阻为
| $ R_{\mathrm{eq}}=\frac{8}{\pi^{2}} R_{\mathrm{L}} $ | (2) |
通过推导得到输出电压为
| $ \dot{\boldsymbol{U}}_{\text {out }}=\frac{R_{\text {eq }}}{R_{\text {eq }}+\dot{Z}_{\text {out }}} \dot{\boldsymbol{U}}_{\text {eq }} $ | (3) |
式中:
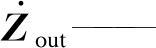 输出阻抗。
输出阻抗。
直流增益Gdc可表示为
| ${G_{{\rm{dc}}}} = \left| {\frac{{{{\mathit{\boldsymbol{\dot U}}}_{{\rm{out}}}}}}{{{{\mathit{\boldsymbol{\dot U}}}_{{\rm{in}}}}}}} \right| = \\ \;\;\;\sqrt {\omega _{\rm{c}}^2} \sqrt {R_{{\rm{eq}}}^2} \sqrt {L_{\rm{m}}^2} \times \\ \;\;\;\left[ {{{\sqrt {\left( { - \frac{1}{{{\omega _{\rm{c}}}{C_{\rm{r}}}}} + {\omega _{\rm{c}}}{L_{\rm{m}}} + {\omega _{\rm{c}}}{L_{\rm{r}}}} \right)} }^2} \times } \right.\\ {\left. {\;\;\;\sqrt {{{\left( { - \frac{{\frac{{{L_{\rm{m}}}}}{{{C_{\rm{r}}}}} - \omega _{\rm{c}}^2{L_{\rm{m}}}{L_{\rm{r}}}}}{{ - \frac{1}{{{\omega _{\rm{c}}}{C_{\rm{r}}}}} + {\omega _{\rm{c}}}{L_{\rm{m}}} + {\omega _{\rm{c}}}{L_{\rm{r}}}}} - \frac{1}{{{\omega _{\rm{c}}}{C_{\rm{r}}}}} + {\omega _{\rm{c}}}{L_{\rm{r}}}} \right)}^2} + R_{{\rm{eq}}}^2} } \right]^{ - 1}}$ | (4) |
为了简化, 令kCr, kLr, k2Lr, k2Lm分别为
| $ \left\{\begin{array}{l} k_{C_{\mathrm{r}}}=C_{\mathrm{r}}^{2} R_{\mathrm{eq}}^{2} \omega_{\mathrm{c}}^{2} \\ k_{L_{\mathrm{r}}}=C_{\mathrm{r}}\left(L_{\mathrm{m}}+L_{\mathrm{r}}\right) \omega_{\mathrm{c}}^{2} \\ k_{2 L \mathrm{r}}=C_{\mathrm{r}}\left(L_{\mathrm{m}}+2 L_{\mathrm{r}}\right) \omega_{\mathrm{c}}^{2} \\ k_{2 L \mathrm{m}}=C_{\mathrm{r}}\left(2 L_{\mathrm{m}}+L_{\mathrm{r}}\right) \omega_{\mathrm{c}}^{2} \end{array}\right. $ | (5) |
可得简化后的直流增益Gdc为
| $ \begin{aligned} G_{\mathrm{dc}} & =\frac{L_{\mathrm{m}} R_{\mathrm{eq}} C_{\mathrm{r}}}{\left|-1+k_{\mathrm{Lr}}\right|} \times \\ & \left[\left(R_{\mathrm{eq}}^{2}+\frac{\left(-1+C_{\mathrm{r}} L_{\mathrm{r}} \omega_{\mathrm{c}}^{2}\right)^{2}\left(-1+k_{2 L \mathrm{m}}\right)^{2}}{C_{\mathrm{r}}^{2} \omega_{\mathrm{c}}^{2}\left(-1+k_{L \mathrm{r}}\right)^{2}}\right)\right]^{-\frac{1}{2}} \end{aligned} $ | (6) |
经过电路模型等效可得电路输入阻抗为
| $ \boldsymbol{Z}_{\mathrm{in}}=-\frac{\mathrm{j}}{C_{\mathrm{r}} \omega_{\mathrm{c}}}+\mathrm{j} L_{\mathrm{r}} \omega_{\mathrm{c}}+ $ |
| $Z_{\mathrm{in}}=-\frac{\mathrm{j}}{C_{\mathrm{r}} \omega_{\mathrm{c}}}+\mathrm{j} L_{\mathrm{r}} \omega_{\mathrm{c}}+ \\ \frac{L_{\mathrm{m}} \omega_{\mathrm{c}}\left[-\mathrm{j}+C_{\mathrm{r}} \omega_{\mathrm{c}}\left(R_{\mathrm{eq}}+\mathrm{j} L_{\mathrm{r}} \omega_{\mathrm{c}}\right)\right]}{-1+C_{\mathrm{r}} \omega_{\mathrm{c}}\left[-\mathrm{j} R_{\mathrm{eq}}+\left(L_{\mathrm{m}}+L_{\mathrm{r}}\right) \omega_{\mathrm{c}}\right]}$ | (7) |
实部ZinR为
| $ Z_{\mathrm{inR}}=\frac{C_{\mathrm{r}}^{2} L_{\mathrm{m}}^{2} R_{\mathrm{eq}} \omega_{\mathrm{c}}^{4}}{k_{C_{\mathrm{r}}}+\left(-1+k_{L_{\mathrm{r}}}\right)^{2}} $ | (8) |
虚部ZinI为
| $ \begin{array}{r} Z_{\text {in }}=\left(1-k_{2 L \mathrm{r}}+k_{C \mathrm{r}}+\omega_{\mathrm{c}}^{2} C_{\mathrm{r}} L_{\mathrm{r}} k_{L \mathrm{r}}\right) \times \\ \frac{L_{\mathrm{m}} \omega_{\mathrm{c}}}{k_{C_{\mathrm{r}}}+\left(-1+k_{L \mathrm{r}}\right)^{2}}-\frac{1}{C_{\mathrm{r}} \omega_{\mathrm{c}}}+L_{\mathrm{r}} \omega_{\mathrm{c}} \end{array} $ | (9) |
谐振变换器一次侧输入电流
| $ i_{L 1}=\frac{U_{\mathrm{in}}}{\sqrt{Z_{\mathrm{inR}}^{2}+Z_{\mathrm{inI}}^{2}}} $ | (10) |
谐振变换器一次侧输出电流
| $ i_{L 2}=\frac{G_{\mathrm{dc}} U_{\mathrm{in}}}{R_{\mathrm{eq}}} $ | (11) |
设一次侧开关管导通电阻与线路电阻之和为Ron, 则一次侧通态功率损耗PMOS1为
| $ P_{\mathrm{MOS} 1}=4 R_{\mathrm{on}} i_{L 1}^{2} $ | (12) |
由于一次侧工作在零电压开关(Zero Voltage Switch, ZVS)区域, 其开关管导通损耗可以忽略, 又因为开关管的关断损耗比较小, 因此可以忽略其关断损耗。
二次侧的损耗PMOS2可以表示为
| $ P_{\text {моs } 2}=4 R_{\mathrm{d}} i_{L, 2}^{2} $ | (13) |
式中:Rd——二次侧开关管导通电阻。
故电路总损耗
| $P_{\text {loss }}=P_{\text {MOS1 }}+P_{\text {MOS2 }}=4 R_{\text {on }} i_{L 1}^{2}+4 R_{\mathrm{d}} i_{L 2}^{2}$ | (14) |
由式(14)可得电路损耗与Ron和Rd相关。由于一次侧开关管起到斩波作用, 其电阻阻值相对稳定, 故可采用减少二次侧开关管电阻的方式, 达到减小电路损耗的目的。
2 同步整流策略
同步整流的主要思想就是在体二极管导通的情况下, 控制开关管同步导通, 降低二次侧开关管导通电阻Rd, 提高转换效率。由于全数字化控制通常采用微控制器(Micro-Controller Unit, MCU)直接进行控制, 但考虑到开关管的导通极其迅速, 会导致MCU来不及响应, 从而失去原有的控制作用, 会对电路造成损害, 因此选择现场可编程门阵列(Field Programmable Gate Array, FPGA)对同步整流进行控制。
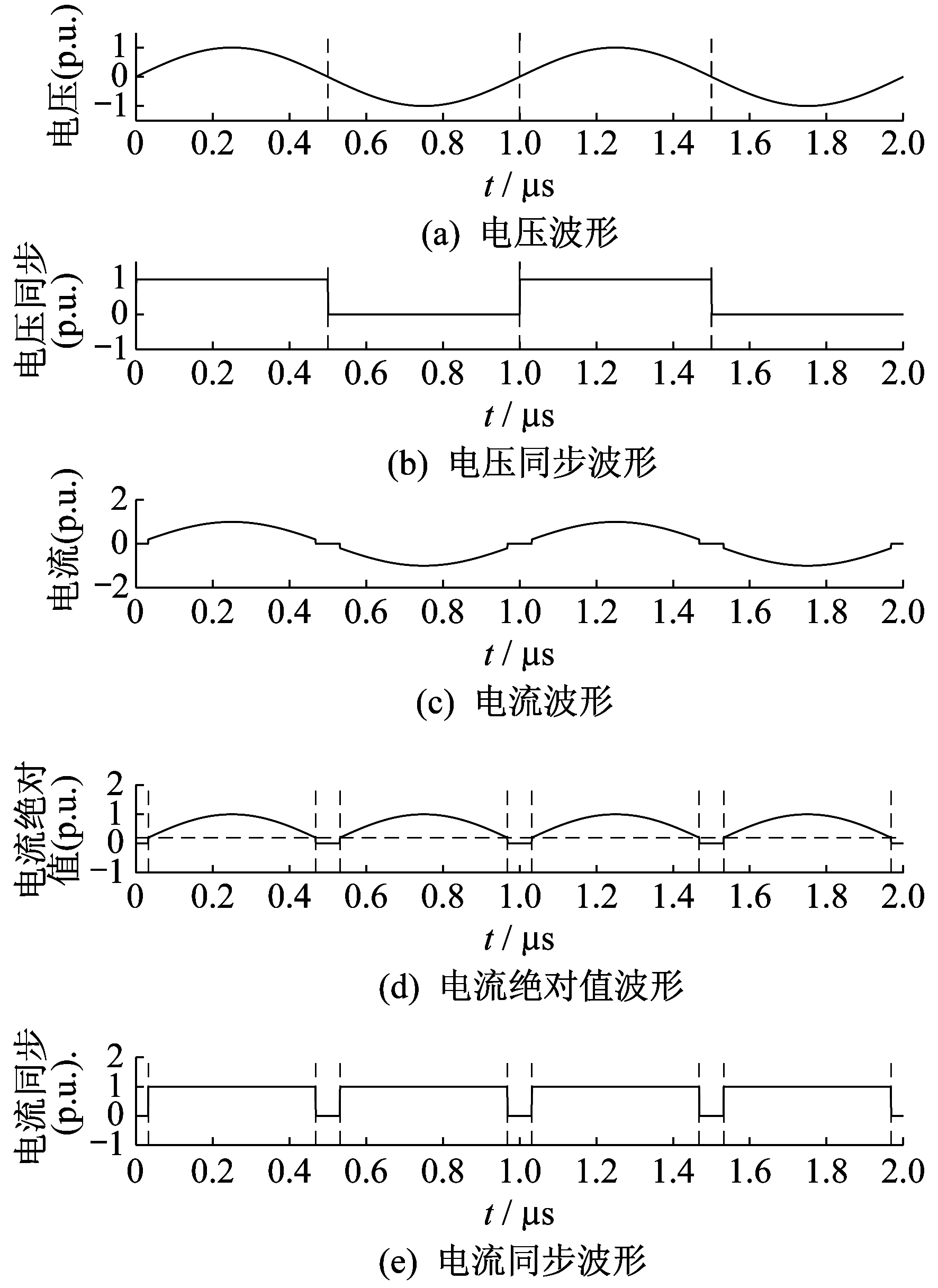
由于CLLC电路工作状态是对称的, 以正向传输功率为例介绍FPGA的工作原理。图 3从上至下依次为Up2电压波形; Up2电压过零比较后的结果; 二次侧电流的波形, 二次侧电流取绝对值的波形, 二次侧电流取绝对值过零比较后的结果。
由图 3可推导出同步整流中二极管导通的真值, 结果如表 1所示。表 1中, 1为高, 0为低。
表 1
二极管导通逻辑真值
| 电压同步 | 电流同步 | 导通二极管序号 |
| 1 | 1 | 1, 4 |
| 0 | 1 | 2, 3 |
| X | 0 | 全关闭 |
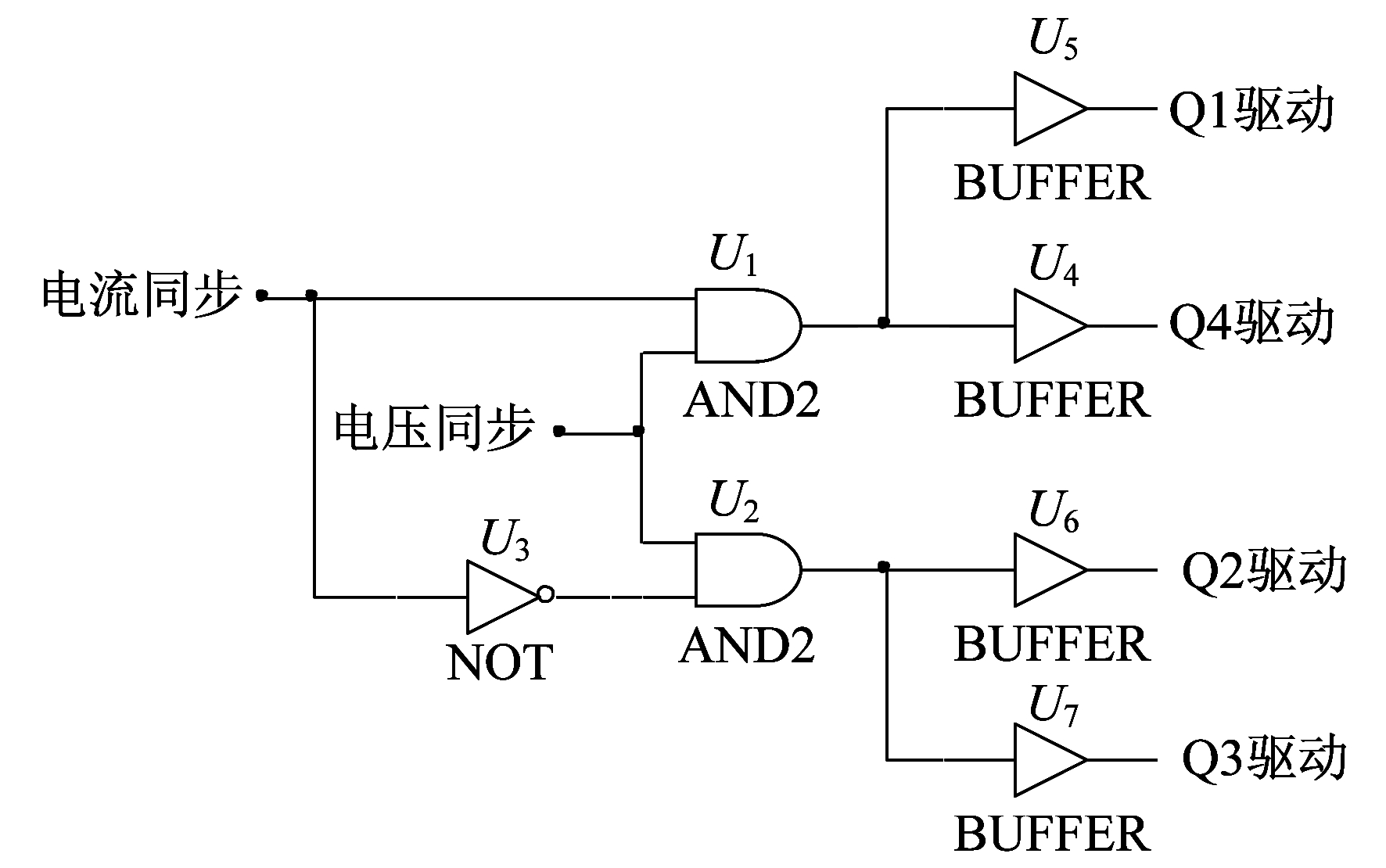
由此可知, 仅需要将Up2电压的极性与电流绝对值的比较结果输入逻辑电路即可完成同步整流。其对应的逻辑设计图如图 4所示。
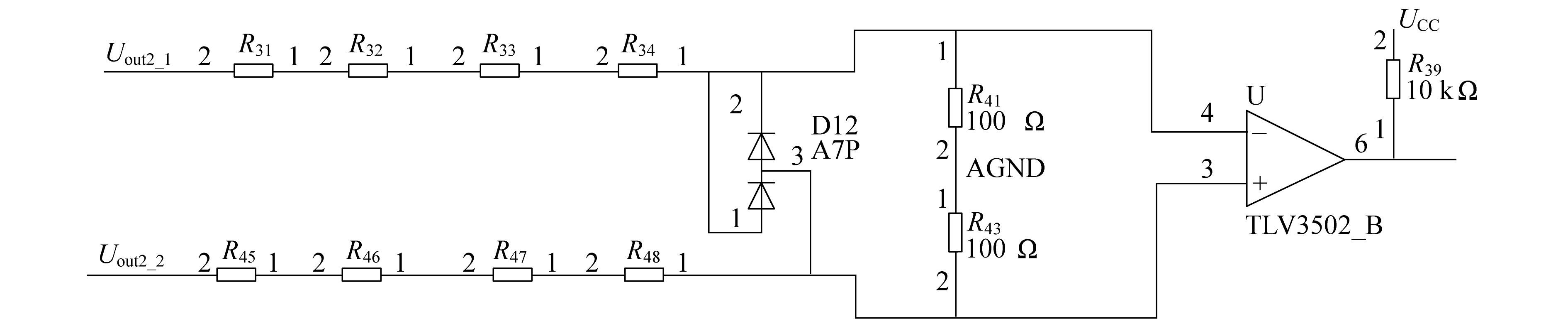
综合考虑隔离等级和成本, 采用差分比较电路对Up2电压极性进行采样。图 5为电压过零点检测电路。当Uout 1≫Uout 2时, 二极管D12导通, 将电压钳位在0.7 V左右, 以避免高压损坏比较器; 当Uout 1≪Uout 2时, 相类似, 电压钳位在-0.7 V。通过此电路, 可直接得到电压过零点, 电阻R31~R34与R45~R48为主回路隔离电阻, 用以隔离主电路的高压。
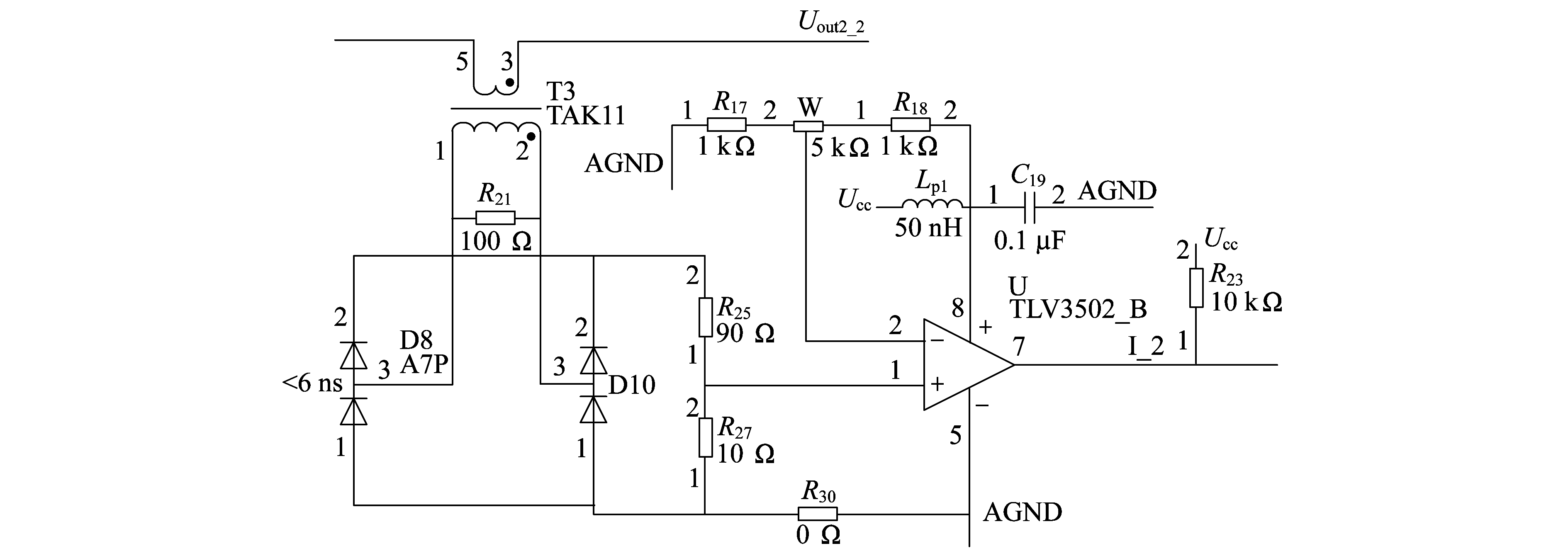
利用高频电流互感器对电流进行采样。电流同步信号采样电路如图 6所示。将一次侧的大电流感应为二次侧小电流, 通过桥式整流电路得到电流信号的绝对值, R25与R27起到分压作用, 避免电压过高损坏比较器, R17和R18与滑动变阻器W构成比较门槛值, 与输入信号进行比较, 得到一次侧电流二倍频信号, 即电流同步信号。
3 实验分析
CLLC谐振变换器的设计规格如下:额定输入电压为400 V, 输入直流电压Uin的范围为350~450 V; 额定输出电压Uout为400 V, 输出电压范围为380~420 V, Uout的纹波要求小于5%;最大输出功率为2.5 kW, 最大输出负载为1 kΩ; 允许的开关频率fc的变化范围为100~300 kHz, 死区时间为200 ns。表 2为主要电子器件选型。
表 2
CLLC电子变压器的器件选型
| 器件 | 功能 |
| TMS320F28069 | 主控芯片 |
| XC6SLX9 | 主控FPGA |
| C3M0065090D | Sic-MOSFET |
| UCC21520 | 驱动芯片 |
| TLV3502 | 高速比较器 |
输出滤波电路采用无极性电容并联电解电容。考虑到输入输出电压接近电解电容450 V的耐压极限, 为了防止电容过压, 采用双电解电容串联, 并且并联均压电阻。CLLC谐振主回路参数如表 3所示。
表 3
CLLC电子变压器的滤波与谐振器件
| 器件 | 设计值 |
| 无极性电容$/ \mu \mathrm{F}$ | 1 |
| 电解电容$/ \mu \mathrm{F}$ | $340(450 \mathrm{V}, 680 \mu \mathrm{F})$ |
| 均压电阻$/ \mathrm{k} \Omega$ | $50(4 \mathrm{W})$ |
| 励磁电感$L_{\mathrm{m}} / \mu \mathrm{H}$ | 71.7 |
| 谐振电感$L_{\mathrm{r}} / \mu \mathrm{H}$ | 17.4 |
| 谐振电容$C_{\mathrm{r}} / \mathrm{nF}$ | 67.1 |
| 变压器变比 | 1: 1 |
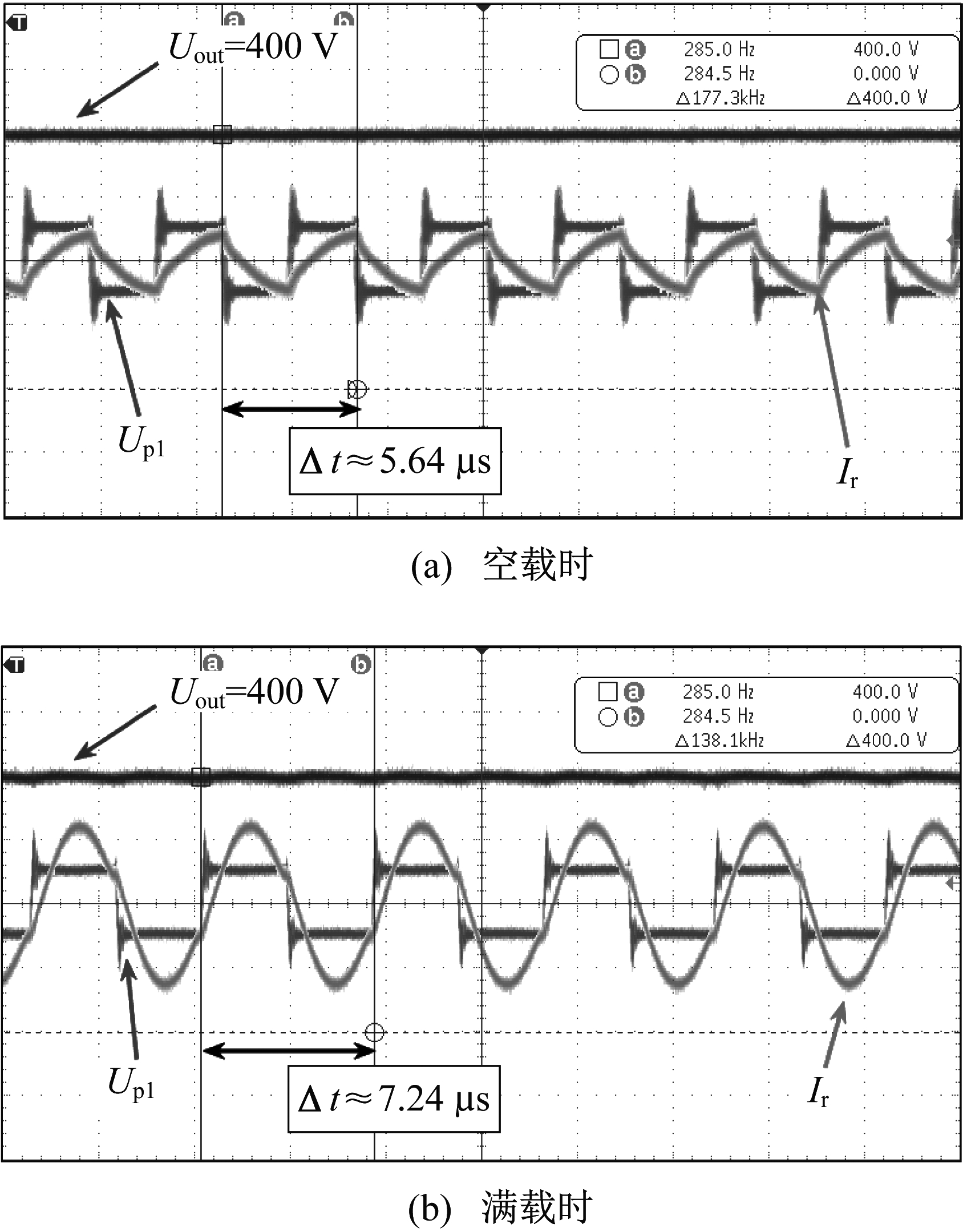
图 7分别展示了空载(输出功率Pout=530 W, fc=177.3 kHz)和满载(输出功率Pout=2.5 kW, fc=138.1 kHz)工况下的输出电压(Uout)、高频方波电压(Up1)和谐振电流(Ir)波形。由图 7可知, 谐振电流Ir相位超前于电压Up1, 电路工作于软开关状态, 且此时输出电压Uout相对恒定, 证明电路可以实现稳压输出。
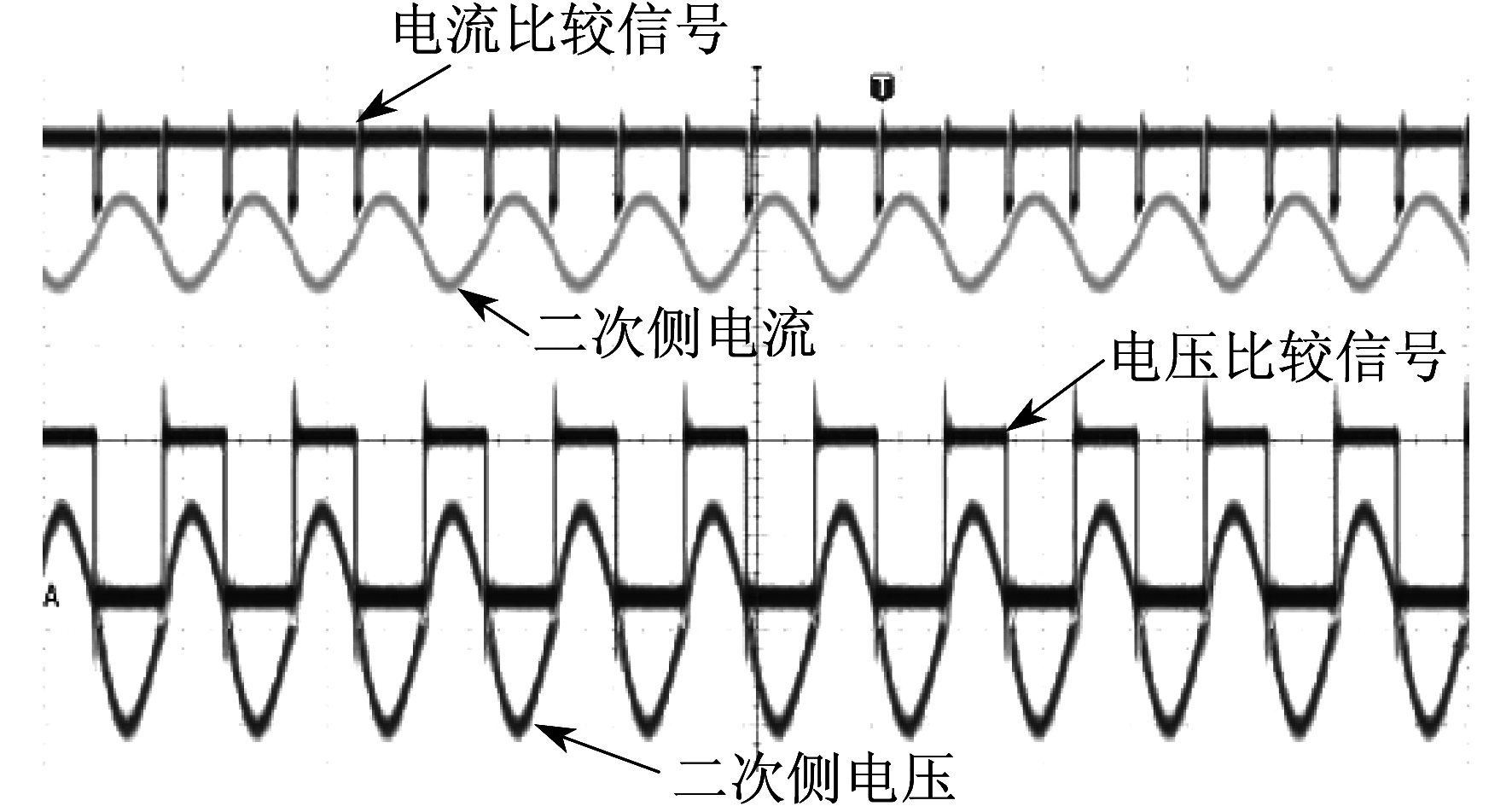
图 8显示的是电流比较信号、二次侧电流、电压比较信号和二次侧电压。由图 8可知, 原始信号与其同步信号无相位偏差, 满足同步整流条件。
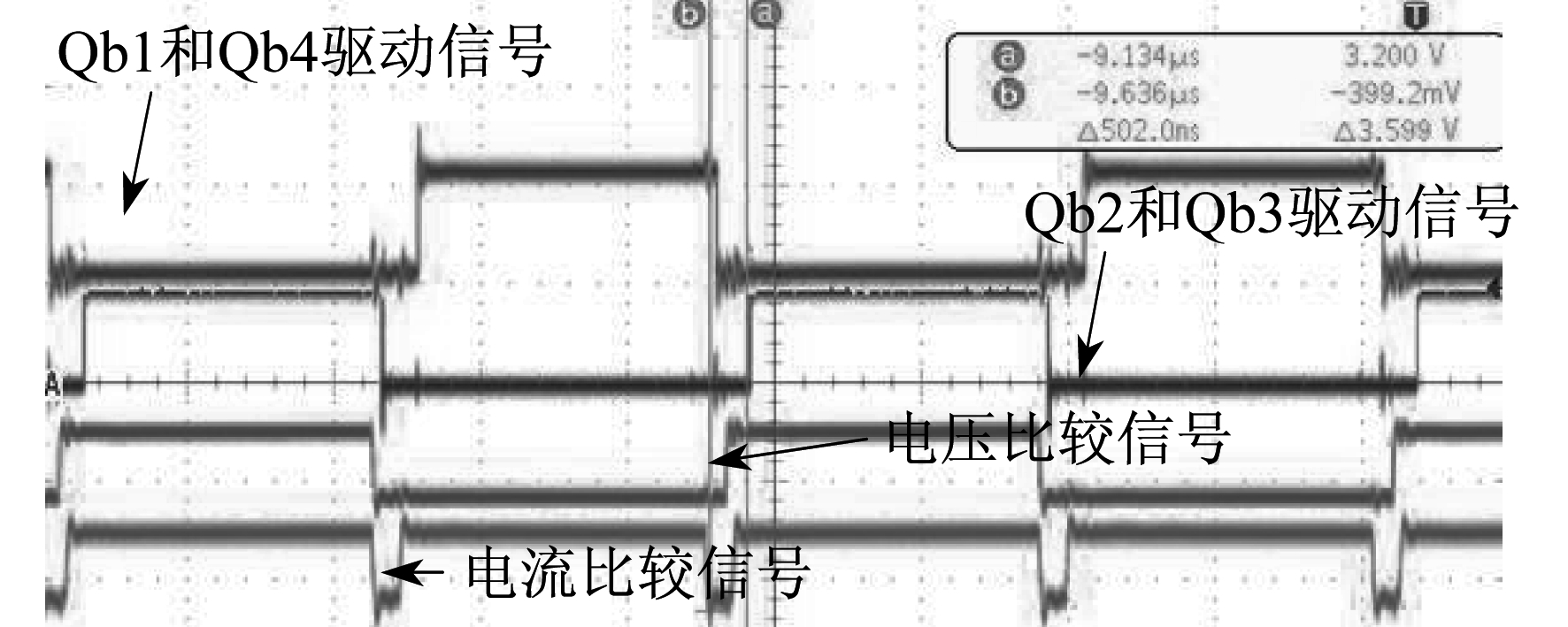
图 9显示的是Qb1和Qb4驱动信号、Qb2和Qb3驱动信号、电压比较信号以及电流比较信号。由图 9可知, 驱动信号与同步信号基本无相差, 满足开关管工作条件。
图 10为采用同步整流与不采用同步整流情况下的效率对比。由图 10可知:在轻载时, 同步整流没有明显提升样机效率, 这是由于轻载时输出电流较小, 故效率提升不明显; 但在重载时, 输出电流较大, 此时同步整流对效率提升明显, 最高可达5%左右。
4 结论
本文提出了一种数字化控制的CLLC变换器同步整流策略, 并通过实验证明该同步整流策略拥有以下3个优点:
(1) 采用全数字化控制, 利用FPGA处理高速信号, 简单有效;
(2) 使用比较器提取主回路信号, 避免使用高速模数转换器转换引入的高成本;
(3) 通过同步整流, 进一步提升了变换器效率, 最高可提升约5%的效率。
参考文献
-
[1]电动汽车蓄电池双向充放电系统的研制[J]. 上海电力学院学报, 2017, 33(1): 44-48.
-
[2]双向DC/DC变换器的设计[J]. 上海电力学院学报, 2017, 33(3): 270-272.
-
[3]直流微网中高降压比软开关DC-DC变换器[J]. 上海电力学院学报, 2015, 31(1): 29-34.
-
[4]第四类LLC谐振变流器模块功能准同构拓扑探求及变形研究[J]. 中国电机工程学报, 2009, 29(9): 35-42. DOI:10.3321/j.issn:0258-8013.2009.09.006
-
[5]DUJIC D, ZHAO C H, MESTER A, et al. Power electronic traction transformer-low voltage prototype[J]. IEEE Transactions on Power Electronics, 2013, 28(12): 5522-5534. DOI:10.1109/TPEL.2013.2248756
-
[6]一种改进的LLC变换器谐振网络参数设计方法[J]. 中国电机工程学报, 2008, 28(33): 6-11. DOI:10.3321/j.issn:0258-8013.2008.33.002
-
[7]FENG W Y, LEE F C, MATTAVELLI P. Optimal trajectory control of burst mode for LLC resonant converter[J]. IEEE Transactions on Power Electronics, 2013, 28(1): 457-466. DOI:10.1109/TPEL.2012.2200110
-
[8]LEE I O, MOON G W. The k-Q analysis for LLC series resonant converter[J]. IEEE Transactions on Power Electronics, 2013, 28(1): 13-16.
-
[9]LLC谐振变换器效率优化设计[J]. 中国电机工程学报, 2013, 33(18): 48-56.
-
[10]ZOU S L, LU J H, MALLIK A, et al. Bi-directional CLLC converter with synchronous rectification for plug-in electric vehicles[J]. IEEE Transactions on Industry Applications, 2018, 54(2): 998-1005. DOI:10.1109/TIA.2017.2773430
-
[11]JUNG J H, KIM H S, RYU M H, et al. Design methodology of bidirectional CLLC resonant converter for high-frequency isolation of DC distribution systems[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1741-1755. DOI:10.1109/TPEL.2012.2213346
-
[12]基于UCD3138的移相全桥同步整流控制策略[J]. 电子世界, 2019(15): 8-10.
-
[13]基于TEA1791A的同步整流电路[J]. 通信电源技术, 2019, 36(7): 26-27.