Print

发布时间: 2020-08-30
摘要点击次数:
全文下载次数:
DOI: 10.3969/j.issn.2096-8299.2020.04.011
2020 | Volume 36 | Number 4




        




  <<上一篇 




  下一篇>> 




基于智能技术的电力系统负荷预测技术研究进展
expand article info 栗风永, 杨洋
上海电力大学 计算机科学与技术学院, 上海 200090
收稿日期: 2020-02-14
基金项目: 国家自然科学基金通用技术联合基金（U1736120）
中图法分类号: TP183;TM715
文献标识码: A
文章编号: 2096-8299(2020)04-0379-06

摘要

负荷预测是智能电网安全领域的热门研究方向。智能技术应用到智能电网负荷预测领域取得了一系列研究成果。首先，对主流负荷预测技术进行总结；然后，将面向智能电网的传统负荷预测技术与近年来新兴的智能负荷预测技术进行对比，并详细介绍了两个领域中典型成果的基本原理和方法；最后，讨论了智能电网负荷预测技术仍需要解决的问题及未来的研究趋势。

关键词

负荷预测; 智能电网; 预测模型; 深度学习

Research Progress of Load Forecasting Technology of Power System Based on Intelligent Technology
expand article info LI Fengyong, YANG Yang
School of Computer Science and Technology, Shanghai University of Electric Power, Shanghai 200090, China

Abstract

Load forecasting is a hot research direction in smart grid.Intelligent technology has been applied to the field of load prediction of smart grid, and a series of research results have been obtained.This paper first summarizes the mainstream load forecasting technologies, then compares the traditional load forecasting technologies with the emerging intelligent load forecasting technologies for smart grids in recent years.Subsequently, the basic principles and methods of typical results in two areas are introduced in detail.Finally, load forecasting issues that need to be addressed and future research trends are further discussed.

Key words

load forecasting; smart grids; prediction model; deep learning

电力负荷预测是指通过模型处理负荷的历史数据和天气数据, 在满足精确度的条件下, 对未来一段时间某个地区的负荷进行预测的方法。提高负荷预测的精确度, 对用电管理、能源消耗的控制、电力系统的经济消耗和社会收益都有着非常重要的意义。电力负荷预测已经成为电力系统管理现代化、智能化必不可少的一环[1-4]。已有的负荷预测方法有很多种, 例如差分自回归移动平均模型(Autoregressive Integrated Moving Average Model, ARIMA)[5]、人工神经网络(Artificial Neural Network, ANN)[6]、支持向量回归(Support Vactor Regerssion, SVR)[7]等。

电力负荷预测在时间跨度上可以分为超短期、短期、中期和长期负荷预测。好的短期负荷预测方法不仅影响合理的发电计划和实时电价, 还方便电力企业对负荷进行及时调整, 使用电企业在进行重要作业时避开用电高峰, 在经济层面对发电厂进行调峰有着重要意义[8]。在规模上, 负荷预测可以分为电网层级的负荷预测和用户层级的负荷预测。电网层级的负荷预测对电力系统的稳定运行和合理改善有着重要的意义。用户层级的负荷预测与售电公司相关, 售电公司需要对用户做出合适的负荷预测, 根据预测结果找出合适的售电方案。与电网层级的负荷预测相比, 用户层级的负荷预测容易受天气和节日等因素影响, 具有较大的随机性, 预测更加困难[9], 所以在不同场景运用不同的预测方法尤为重要。

近些年迅速发展的软硬件技术, 使得针对智能电网的负荷预测新兴技术和方法不断涌现, 无论是将传统算法与新的算法相结合, 还是将大数据和深度学习等现代热门技术积极引入, 都取得了众多创新性的成果。本文对传统负荷预测技术和新兴负荷预测方法进行对比, 分析了这些方法的原理、流程、优势及不足; 最后对未来的研究方向提出了建议。

1 线性回归预测模型

负荷预测主要是根据历史负荷数据归纳出负荷规律, 然后通过线性回归方法建立预测模型, 计算出未来某一时刻的负荷数据。其模型为

$ \mathit{\boldsymbol{Y}}\left( t \right) = \mathit{\Psi }(\mathit{\boldsymbol{X}}\left( t \right), \Delta \left( \theta \right)) $ (1)

式中:$\mathit{\boldsymbol{Y}}\left(t \right)$——预测数据序列;

$\mathit{\Psi }$(·)——构建的预测模型;

$\mathit{\boldsymbol{X}}\left(t \right)$——已知数据序列;

Δ($θ$)——调整模型精确度的一系列参数项。

由于各个场景的用电特征不同, 使用的预测模型与方法也有所不同[8]。若数据的自变量与因变量之间存在着明显的线性相关关系, 则可建立线性回归模型进行预测:

$ y\left( t \right) = {b_0} + {b_1}{x_{i1}} + {b_2}{x_{i2}} + \ldots + {b_n}{x_{in}} + \theta $ (2)

式中:$y(t)$——$t$时刻预测的负荷值;

${x_i}_1, {x_i}_2, {x_i}_3, \ldots, {x_i}_n$——影响负荷值的因素;

${b_0}, {b_1}, {b_2}, \ldots, {b_n}$——回归方程的回归系数;

$θ$——随机干扰项。

尽管现在的负荷预测拥有强大的科学理论基础, 但负荷预测存在以下特点:不确定性, 由于负荷受到众多因素的影响, 人们无法将这些因素全部考虑进去, 导致预测结果不确定; 条件性, 只有在满足一定的条件下才能对未来进行预测; 时间性, 每种负荷预测方法都具有一定的时间范围, 在进行负荷预测时, 需要指定预测的时间范围; 多方案性, 不同情况下的预测模型通常不一致, 可能会得出多种预测方案。

2 主流负荷预测方法

主流负荷预测技术主要围绕两个范畴展开, 即传统负荷预测方法和智能负荷预测方法。传统负荷预测是指利用传统的机器学习方法对智能电网中的电力负荷数据进行处理; 而智能负荷预测主要是利用新兴的深度神经网络模型和大数据处理技术对大规模的电力负荷数据展开预测。

2.1 传统负荷预测方法

2.1.1 回归分析法

回归分析法是根据影响负荷的因素与负荷之间的关系, 建立负荷数据之间的关系式, 构造相应的回归预测模型。回归分析法大致可分为两种:线性回归法和非线性回归法, 其中线性回归法主要包括一元线性回归和多元线性回归。

文献[10]将KOENKER R等人提出的分位数回归[11]与BREIMAN L提出的随机森林[12]相结合, 提出了一种基于分位数回归森林模型。该模型可以提前24 h对短期负荷概率密度进行预测。通过考虑每个决策树中每个叶节点的观测值, 在随机森林中生成K决策树, 之后根据给定的参数遍历所有决策树, 计算每棵决策树观测值的权重, 再利用这些权重计算分布函数的估计。分位数回归森林模型可以转换为以下优化问题。

$ \begin{array}{*{20}{l}} {\mathop {\min }\limits_\mathit{\boldsymbol{\beta }} \sum\limits_{i = 1}^N {{\rho _\tau }} \left( {{Y_i} - \mathit{\boldsymbol{X}}_i^\prime \mathit{\boldsymbol{\beta }}} \right) = }\\ {\mathop {\min }\limits_\mathit{\boldsymbol{\beta }} \sum\limits_{i\mid {Y_i} \ge \mathit{\boldsymbol{X}}_i^\mathit{\boldsymbol{\beta }}\mathit{\boldsymbol{\beta }}} \tau \left| {{Y_i} - \mathit{\boldsymbol{X}}_i^\prime \mathit{\boldsymbol{\beta }}} \right| + }\\ {\sum\limits_{i\mid {Y_i} < \mathit{\boldsymbol{X}}{'_i}\mathit{\boldsymbol{\beta }}} {(1 - \tau )} \left| {{Y_i} - \mathit{\boldsymbol{X}}_i^\prime \mathit{\boldsymbol{\beta }}} \right|, 0 < \tau < 1} \end{array} $ (3)

式中:$\mathit{\boldsymbol{\beta }}$——回归系数向量;

$N$——样本数量;

${{\rho _\tau }}$——分位数回归的损失函数;

$τ$——分位数;

${{Y_i}}$——因变量;

${\mathit{\boldsymbol{X}}_i^\prime \mathit{\boldsymbol{\beta }}}$——因变量$Y$在自变量${{\mathit{\boldsymbol{X}}_\mathit{i}}}$下的分位数。

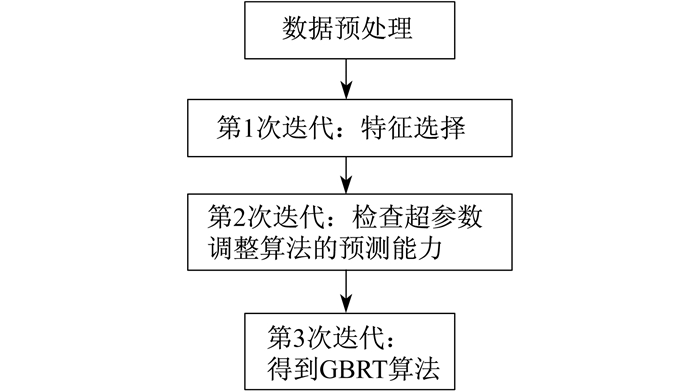
文献[13]提出了优化的梯度增强回归树(Gradient Boosting Regression Trees, GBRT)算法。该算法使用了3次迭代构造预测模型。第1次迭代选择出数据集的重要特征, 第2次迭代检查了特征选择数据集上6种超参数调整算法的预测能力, 第3次迭代使用了特征工程和超参数调整。算法流程如图 1所示。



图 1 GBRT算法流程图

苏丽等人[14]针对Lyapounov最大指数法嵌入维数提出了一种自回归误差算法, 在原方法的基础上对求嵌入维数进行改进, 使用偏离平方和取代之前的主观判断, 作为对所得数据进行离散程度判断的指标, 克服了人为嵌入维数取值造成的不准确问题。

回归分析模型由于构造简单, 所需参数较少, 所以预测速度相比较快, 比较容易理解。但是对于历史数据的要求高, 需要寻找合适的参数, 且很多实际因素的影响没有考虑进去, 导致准确度相对较低。

2.1.2 时间序列法

时间序列法是目前电力负荷预测中一种比较成熟的方法。在电力负荷预测中, 所使用的历史数据都是按照一定的时间间隔进行采集的, 这些数据构成有序集合, 形成了一个时间序列。根据负荷的历史数据来建立负荷随时间变化的数学模型, 就可以确立负荷预测的表达式, 预测未来的负荷波动情况。

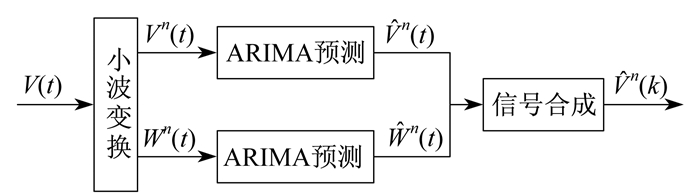
张然然等人[15]提出了一种小波变换与差分自回归移动平均模型相结合的方法。该方法的建模原理如图 2所示。其中$V$($t$)为原始的时间序列信号, 通过小波变换[16]将其分解为概况信号${V^n}(t)$和细节信号${W^n}(t)$, 分别对${V^n}(t)$和${W^n}(t)$建立ARIMA模型, 再进行$k$步的超前预测得出${\widehat V^n}(t)$与${\widehat W^n}(t)$, 最后通过加权求和得到最终的预测值${V^n}(t)$。



图 2 基于小波变换的ARIMA建模原理

文献[17]中利用MARS(Multivariate Adaptive Regression Splines)、SVR和ARIMA模型对短期电力负荷进行综合预测。MARS模型中$X$和$y$之间的关系如式(4)所示; 对于SVR, 非线性回归问题通过优化可得到非线性回归函数如式(5)所示; ARIMA模型计算如式(6)所示。

$ y=\hat{f}(X)=a_{0}+\sum\limits_{m=1}^{M} a_{m} \mathrm{BF}_{m}(X) $ (4)

$ f(X)=\sum\limits_{i=1}^{N}\left(\alpha_{i}-\alpha_{i}^{*}\right) K\left(x_{i}, x_{j}\right)+b $ (5)

$ \begin{array}{c} y_{t}=c+a_{1} y_{t-1}+\cdots+a_{p} y_{t-p}+u_{t}+ \\ m_{1} u_{t-1}+\cdots+m_{q} u_{t-q} \end{array} $ (6)

式中:${a_0}$——常数;

${{a_m}}$——模型系数;

${\rm{B}}{{\rm{F}}_m}(X)$——样条函数;

${{\alpha _i}, \alpha _i^*}$——拉格朗日乘数和;

$K\left({{x_i}, {x_j}} \right)$——描述$D$维特征控件中内积的内核函数;

$b$, $c$——常数;

${a_1}, {a_2}, {a_3}, \ldots, {a_p}$——AR参数;

${m_1}, {m_2}, {m_3}, \ldots, {m_q}$——MA参数;

$p$, $q$——自回归项和移动平均值;

${u_t}, {u_{t- 1}}, {u_{t- 2}}, \ldots, {u_{t - q}}$——误差项。

时间序列法的优势是所需的历史数据和工作量较少, 所以预测速度比较快, 能够反映出负荷在短期时间内变化的连续性。但该方法建模过程较复杂, 且要求较高的时间序列平稳性, 所以一般只在负荷变化比较均匀的短期负荷预测中使用。此外, 该方法对天气、节假日等不确定性因素考虑不足, 所以预测误差相对较大。

2.1.3 灰色模型

灰色预测是以灰色理论为基础, 模型中并不使用负荷的原始历史数据, 而是使用生成的数据序列。灰色预测的核心体系是灰色模型(Grey Model, GM), 即对原始负荷的历史数据进行累加或者使用其他方法得到近似的指数规律, 再进行建模, 常用的灰色模型为GM(1, 1)(一阶微分方程, 包含一个变量)[18]。

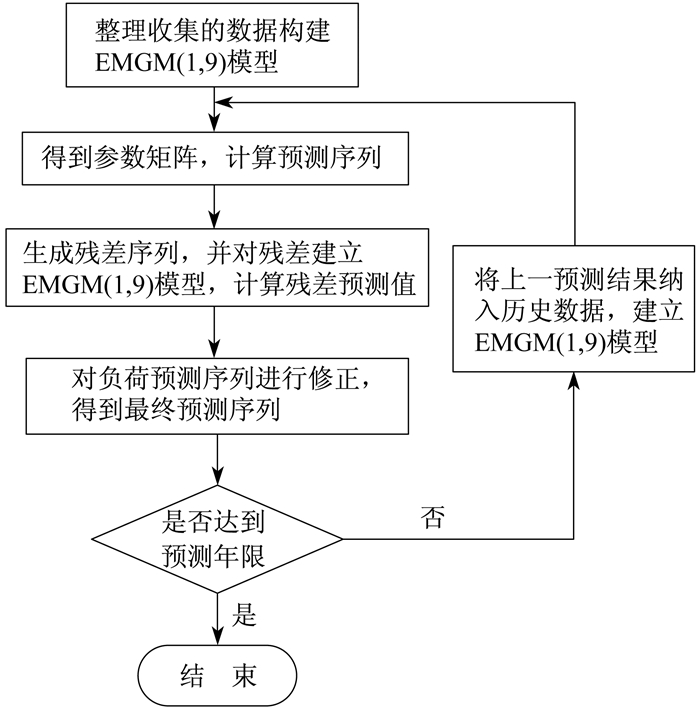
文献[19]提出了一种电力负荷预测的残差修正灰色模型(Error Modification Grey Model, EMGM)。图 3描述了其对应的流程。



图 3 灰色优化模型流程

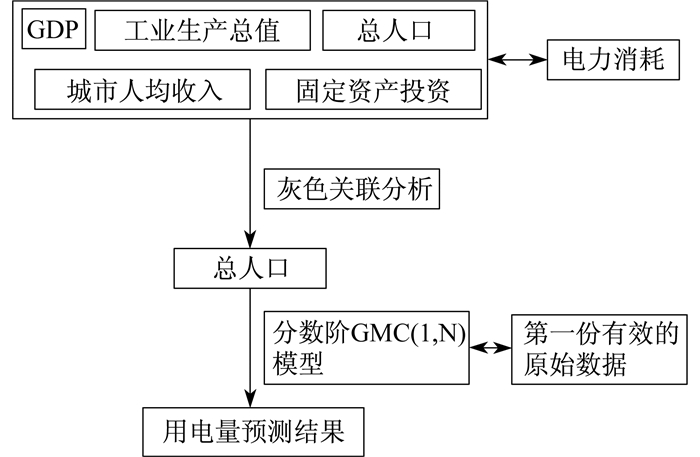
文献[20]利用面积坐标和中点线坐标的几何坐标特征, 提出了基于分数阶累积法的区间灰数序列的灰色预测模型。文献[21]在TIEN T提出的带卷积积分的灰色预测模型[GMC(1, N)][22]的基础上, 将分数阶累加生成操作序列引入, 使用灰色凸相关分析方法描述了电力消费与相关因素之间的关系, 提出了一种考虑总人口的多变量灰色预测模型。其操作流程如图 4所示。



图 4 考虑总人口的多变量灰色预测模型操作流程

灰色预测的优点是不需要太多数据, 从而使得其在生成新的数据序列时耗时较少。正是由于使用的是新生成的数据序列, 不用特别考虑原始数据的分布规律和变化规律, 所以常适用于短中期负荷预测。但该方法不足之处在于, 当数据的趋势或离散程度波动较大时, 预测结果误差较大[23]。

2.2 智能负荷预测方法

2.2.1 神经网络模型

作为新兴的负荷预测方法, 神经网络模型首先在图像识别、自然语言处理等方面大量使用。在负荷预测方面, 神经网络模型能够准确地分析负荷与天气和节日之间的关系[24-25]。

神经网络中包含着大量的神经元, 神经元可以通过非线性函数将输入映射到输出。在预测负荷数据的过程中, 神经网络选取过去一段时间的历史数据为训练样本, 构建合适的网络结构, 再用某种训练算法对其进行训练, 在满足精度要求之后用于负荷预测。在负荷预测中应用最多的是人工神经网络(Artificial Neural Networks, ANN)和递归神经网络(Recurrent Neural Networks, RNN)。

文献[26]提出了一种基于混合深度神经网络的负荷预测模糊集成模型, 先用模糊聚类对历史数据进行分类, 再用径向基函数的输出结果作为卷积神经网络的输入进行预测。文献[27]提出了一种基于神经网络和多目标优化的电力系统负荷预测混合模型。文献[28]提出了一种基于小波变换的神经网络优化方法, 并且说明了如何对改进的Bat算法的短期负荷预测进行数据选择。即先将选择后的数据预处理, 选择出最佳的母小波候选, 确定ANN架构的最佳参数, 将小波变换作为适当的过滤阶段(第一个Bat算法优化层); 之后对ANN训练和验证性能(模型拟合)进行评估; 最后对人工神经网络进行训练, 通过将蝙蝠算法[29]和比例共轭梯度算法相混合, 提高神经网络学习的准确性(第二个优化层)。文献[30]将递归卷积神经网络用于多短期负荷预测。一维卷积神经网络为

$ \begin{aligned} O_{i}^{l}=& \operatorname{ReLU}\left(\mathrm{BN}\left(O^{l-1} * F^{l}\right)_{i}\right)=\\ & \operatorname{ReLU}\left(\mathrm{BN}\left(\sum\limits_{m} O_{i+m}^{l-1} * F_{m}^{l}\right)\right) \end{aligned} $ (7)

式中:$O_i^l$——第$l$层中的第$i$个值;

*——权重取反的卷积;

${{\rm{BN}}}$, ${\mathop{\rm ReLU}\nolimits} $——批次归一化和整流线性单位激活函数。

当特征图$l$-1层的宽度为$W$, 高度为1, 通道为$C$, 表示为${O^{l- 1}} \in {R^{W \times 1 \times C}}$, 参数${F^l} \in {R^{k \times 1 \times C}}$在第l层中的“权重”是通过梯度下降法学习的权重, 用于标识局部模式。

神经网络模型对大量的非线性结构、非精确的规律具有较好的自适应性, 分类准确度学习能力和计算能力较高; 缺点是模型搭建较为复杂, 需要的参数较多, 导致学习过程比较长, 有可能陷入局部最小值, 需要优化学习过程。

2.2.2 支持向量机模型

支持向量机(Support Vector Machine, SVM)是一种为解决分类问题而提出的机器学习方法, 目的是为了寻找出最合适的超平面来对数据进行分类[31-32]。在使用SVM进行负荷预测时, 需要先对数据进行预处理, 选择合适的核函数以及参数, 再使用数据对SVM模型进行训练和测试来评估模型, 之后才能对负荷进行预测。

文献[33]提出了一种基于特征选择的短期电力负荷预测方法最小二乘支持向量机, 通过自相关函数(Autocorrelation Function, ACF)与灰狼优化算法(Grey Wolf Optimizer, GWO)对历史数据进行优化, 提取特征性较强的数据, 再使用最小二乘支持向量机进行预测, 式(8)为自相关函数, 优化式(9)为最小二乘支持向量机优化。

$ \begin{array}{l} {r_k} = r\left( {{X_t}, {X_{t - k}}} \right) = \\ \;\;\;\;\;\;\frac{{\sum\limits_{t = k + 1}^n {\left( {{X_t} - \bar X} \right)} \left( {{X_{t - k}} - \bar X} \right)}}{{\sum\limits_{t = 1}^n {{{\left( {{X_t} - \bar X} \right)}^2}} }}. \end{array} $ (8)

$ \begin{array}{*{20}{l}} {{\mathop{\rm Min}\nolimits} J(w, e) = \frac{1}{2}{w^{\rm{T}}}w + \frac{1}{2}\gamma \sum\limits_{i = 1}^N {e_i^2} }\\ {{\rm{ subject\; to }}\;{y_i} = {w^{\rm{T}}}\phi \left( {{x_i}} \right) + b + {e_i}\quad i = 1, 2, 3, \cdots , N} \end{array} $ (9)

式中:${r_k}$——滞后$k$的自相关系数;

$t, t-k$——时间序列;

$w$——权重;

${{e_i}}$——非负的松弛变量;

$b$——偏差项;

$γ$——惩罚参数。

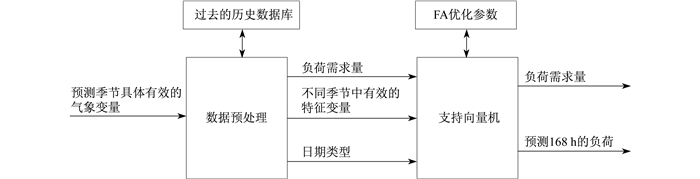
文献[34]引入了相似度概念, 用支持向量机与萤火虫算法(Firefly Algorithm, FA)[35]混合优化SVM的参数, 提出了一种模糊支持向量机进行负荷预测, FA-SVM方法的算法流程如图 5所示。



图 5 FASVM方法的算法流程

文献[36]提出了一种基于支持向量回归的序贯网格法, 根据给定的数据集, 在SVR建模处理中用其预测性能作为因变量, 用回归曲面的3个参数作为自变量, 提出了一种新颖的网格算法, 不仅为拟合参数回归曲面提供了一种新的方法, 而且还可以通过引入参数的固定网格点的渐近正态性作出统计推断。

SVM的优点是泛化能力强, 全局最优, 可以很好地处理高维数据集, 解决局部最小值问题。但该方法对于参数和核函数的选择基于经验, 有较大的人为因素; 并且缺乏对模糊现象的处理能力, 使得预测值和真实值之间存在差距[37]。

2.3 传统与智能负荷预测方法的比较

通过对比分析传统负荷预测方法和新兴负荷预测方法可以发现, 两种方法各有优缺点。结合实际应用的场景和相关数据的变化情况, 可以得到如下结论:当历史数据的变化有比较明显的趋势和规律性时, 可以建立回归分析模型和灰色预测模型, 因为它们计算简单, 所需时间较少, 有比较好的预测效果; 当历史数据比较少或者需要进行中长期预测时, 使用灰色模型或者一些较为简单的回归分析模型有比较好的效果; 而在历史数据比较充足, 并且数据的无规律性较强时, 可以通过构建深度神经网络模型和支持向量机模型来进行预测[38-40], 保证预测的数据具备较高的精度。

3 结语

为了使得电力负荷预测更加精确与快速, 探索新的预测模型成为未来亟需开展的工作。结合现有问题及新技术的发展, 未来可以从以下几个方面进行:提出高效的数据优化方法; 确定影响负荷变化的新因素; 引入新兴数据处理技术。

由于不必要因素引起偶尔的用电量不规律, 数据采集过程中会有较多的异常值, 部分不合适的特征数据可能导致构建出的模型不够精确, 所以对数据进行优化很有必要。

常见的影响负荷变化的因素如天气、节假日、温度等对于负荷来说影响比较直观, 之后的研究应该多关注一些突发事件。若能在预测模型中融入对突变负荷的预测, 将会提升智能电网的稳定性。

未来的负荷预测应与大数据更加紧密地结合, 以提高预测结果的精确度, 推进智能电网的健康发展。

参考文献