|
|
|
发布时间: 2020-10-30 |
清洁发电 |
|
|
|
收稿日期: 2020-05-18
基金项目: 中国华能集团有限公司2019年度科技项目(K-522019007)
中图法分类号: TK228
文献标识码: A
文章编号: 2096-8299(2020)05-0445-06
|
摘要
针对火电厂锅炉再热器欠温问题存在的故障隐患,研究了随机森林、极端随机树和梯度提升决策树3种集成学习算法对再热蒸汽温度的预测效果。再通过预测值与真实值之间存在的残差,可以在一定程度上反映故障隐患信息。采用滑动窗口法精确计算预警阈值,分别对3种算法的预警效果进行了对比分析,确定了极端随机树与滑动窗口法相结合的预警模型初始报警时刻最早,预测效果最为准确。
关键词
极端随机树; 再热蒸汽; 滑动窗口法; 故障预警
Abstract
Aiming at the hidden troubles of under-temperature problems of boiler reheaters in thermal power plants, the prediction effects of three integrated learning algorithms, extreme random tree, gradient boost and random forest, on the temperature of reheated steam were studied.The residual between the predicted value and the real value reflects the hidden danger information to a certain extent; at the same time, the sliding window method is used to accurately calculate the warning threshold, and the early warning effects of the three algorithms are compared and analyzed, and the extreme random tree and sliding window are determined.
Key words
extreme random tree; reheated steam; sliding window method; fault warning
蒸汽再热技术已经广泛应用于超临界机组。再热指的是从汽轮机高压缸出口出来的蒸汽, 经过再热器进一步加热后, 使蒸汽的焓和温度达到设计值, 再返回汽轮机中的低压缸做功的过程。再热器的作用是提高电厂循环的热效率, 并将汽轮机末级叶片的蒸汽温度控制在允许的范围内。这样既可以降低水蒸气的湿度, 又可以提高汽轮机的相对热效率和绝对热效率。然而, 汽轮机通流部分的改造往往会降低再热器进口蒸汽温度, 导致再热器出口气温达不到设计参数, 就会出现再热器欠温现象。如果再热器出口温度存在明显欠温, 将会对机组造成两方面危害[1]:一是由于降低了平均温差, 使汽轮机效率下降, 影响了电厂的经济性[2]; 二是由于温度降低, 根据朗肯循环, 汽轮机内蒸汽的湿度会提高, 湿蒸汽中的水珠将侵蚀汽轮机叶片, 使叶片的背面产生麻点和缺痕, 降低汽轮机的使用寿命, 危害设备的安全运行。因此, 如果在再热器欠温故障发生前就捕捉到细微的故障征兆, 发出预警信号, 就可以大大提高火电机组运行的安全性和经济性, 减少再热器欠温引起的安全事故。
故障预警是指根据安全仪表系统(Safety Instrumentation System, SIS)保存的设备监测数据, 采用合适的预警算法, 在设备故障发展初期判断出设备存在的故障隐患, 并发出预警信号, 其重点在于预测。近年来, 发电设备的故障预警在国内成为一个研究热点, 高校和企业均开展了这方面的研究。刘鑫沛等人[3]采用了改进过程记忆矩阵的多元状态估计方法, 并将其与聚类分析相结合, 很好地实现了制粉系统早期故障预警, 但在样本量较大时, 要获得聚类结论有一定的困难; 朱麟海[4]以透平出口排温为切入点, 利用支持向量机的方法建立了燃机高温部件预警模型, 但支持向量机同样存在对大规模训练样本难以实施的困难; 魏书荣等人[5]研究了海上风电机组的故障诊断与状态检测, 利用温度时序图分析, 分为正常运行、故障形成、即将发生故障3种状态进行监测, 采用神经网络与遗传算法相结合的方法进行了故障诊断; 黄伟等人[6]针对燃气-蒸汽联合循环电站中燃气轮机燃烧室故障问题, 采用相似度分析法, 并结合非线性状态估计技术进行了燃烧室故障预警研究。国外对发电设备故障诊断的研究较为成熟, 如TAYARAIN-BATHAIE S S等人[7]采用神经网络对燃气轮机进行了故障诊断与分离; SALAHSHOOR K等人[8]采用了多数据融合的故障诊断法, 并将该方法应用于工业涡轮机。本文比较了不同的机器学习算法对火电厂再热器的故障预警效果, 利用智能算法的预测功能对再热器欠温故障进行预警, 将残差是否超过滑动窗口法预设的预警阈值作为发出报警的判据, 提前发出报警信号。
1 故障预警系统结构
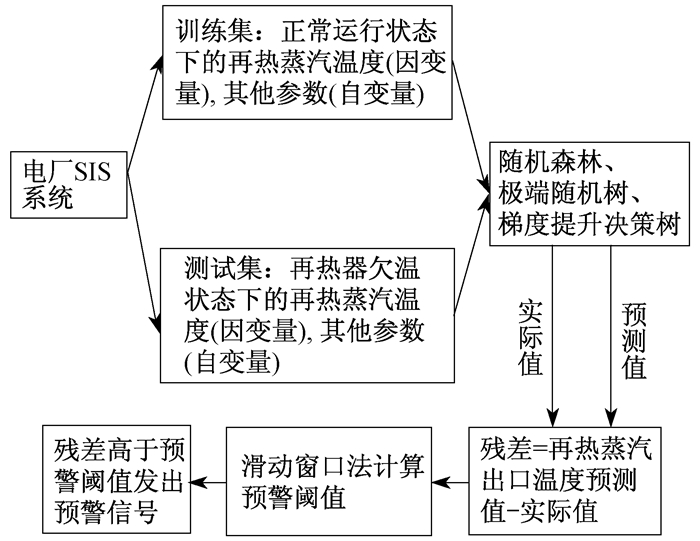
再热器欠温故障预警系统的结构如图 1所示。首先, 选取与再热蒸汽欠温故障相关的监测参数作为自变量, 以再热器出口温度为因变量; 然后, 从SIS系统提取数据输入随机森林(Random Forest, RF)、极端随机树(Extra-trees, ET)和梯度提升决策树(Gradient Boost Decision Tree, GBDT)中。将再热器正常运行状态下提取出的数据作为训练集, 3种算法分别对训练集中自变量与因变量之间的关系进行学习; 将再热器欠温状态下提取出的数据作为测试集, 此时再热器处于故障隐患状态, 其再热蒸汽出口温度预测值必然偏离其真实值, 预测值与真实值之间的差值称为残差。利用滑动窗口法对残差进行处理形成预警阈值后, 残差一旦超过预警阈值立即发出报警信号, 提醒运行人员处理。
2 3种预测算法介绍
常用的传统预测模型有灰色预测、回归预测、时间序列预测3种。目前, 人工智能算法更广泛地应用于预测中, 因此本文分别采用机器学习中的随机森林、极端随机树、梯度提升决策树对再热器出口气温进行趋势预测。
2.1 随机森林
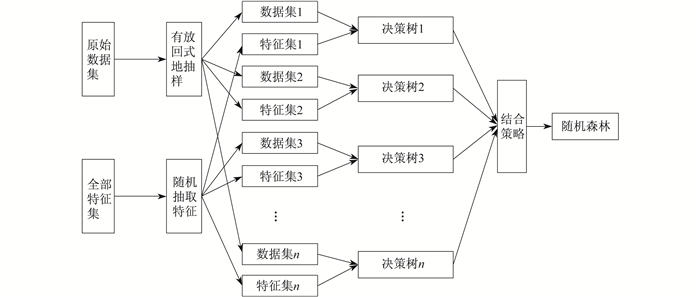
随机森林由伯克利大学教授BREIMAN L和CUTLER A于2001年共同提出[9]。该方法属于两层算法组成的集成方法。这种集成方法以二元决策树作为基学习器, 以自举集成(bagging)作为上层算法。随机森林的随机体现在:从训练集中取数据时是随机抽取的; 在构建决策树时是从整体数据集中随机选取特征的。这两步随机使得随机森林在训练时避免了过拟合现象。它利用自举取样(bootstrap)的方法在数据集的子集上训练出一系列模型, 这些子集是从训练数据集中随机抽取的。随机森林的算法流程如图 2所示。
具体的算法步骤如下。
步骤1 从N组原始样本集中利用bootstrap的方法从数据集有放回式地随机抽取M组训练样本, 针对每一个训练样本分别构建基学习器(二元决策树模型)构成的组合模型, 即
| $ \left\{h\left(X, \boldsymbol{\theta}_{j}\right), j=1, 2, 3, \cdots, K\right\} $ | (1) |
式中:X——解释变量;
θj——独立同分布的随机矢量;
K——决策树的棵数。
从故障样本中抽取数据作为测试样本集来验证模型的准确性。
步骤2 设Y为被解释变量, 取组合模型的平均值作为Y的预测值, 用(X, Y)构成随机森林的训练集。由于构成随机森林的训练集是从随机向量X和Y的分布中独立抽取的, 因此数值型预测值h(X)的推广误差均为EX, Y(Y-h(X))2。
假设原始样本集中有P个输入变量, 则在每棵决策树的每个节点从P个输入变量中随机抽取mtry(mtry为节点值)个变量作为子集分裂, 再根据分枝优度准则选择最佳分枝。
步骤3 每棵决策树开始自上向下采用分类与回归树(Classification and Regression Tree, CART)方法递归分枝且不进行剪枝处理, 叶节点的最小尺寸设定为5, 以此作为决策树生长的终止条件且确保模型建立的准确性。
步骤4 将生成的M棵决策树以bagging方法组成随机森林回归模型, 其模型的准确性采用故障数据预测的均方误差(MSE)和平均绝对误差(MAE)来评价。
2.2 极端随机树
极端随机树也是一种集成的机器学习算法[10]。该算法用{T(V, X, D)}表示, 其中T为最终的分类器模型, D为数据样本集, V为基分类器的数量。每个基分类器根据输入样本X={x1, x2, x3, …, xM}产生预测结果。极端随机树算法的步骤如下。
步骤1 给定原始数据样本集D, 样本数量S, 特征数量W。在极端随机树的分类模型中, 每个基分类器使用全部的样本进行训练。
步骤2 根据CART决策树算法生成基分类器。为增强随机性, 在每个节点分裂时随机从W个特征中选取m个特征, 对每个节点选择最优属性进行节点分裂, 分裂过程不减枝。对分裂产生的数据子集再迭代执行步骤2, 直至生成一棵决策树。
步骤3 重复步骤1和步骤2迭代V次, 生成V棵决策树以及极端随机树。
步骤4 对生成的极端随机树使用测试样本生成预测结果。
极端随机树是对随机森林的改进。随机森林是对数据行的随机, 而极端随机树是对数据行与列的随机得到分叉值, 从而进行对回归树的分叉。因此, 同样是集成学习算法, 极端随机树的泛化能力高于随机森林。此外, 极端随机树中的每一棵回归树用的是全部训练样本, 在节点分割上随机选择分割属性, 增强了基分类器节点分裂的随机性。
2.3 梯度提升决策树
梯度提升决策树(以下简称“梯度提升法”)是由斯坦福大学的教授FRIDEMAN J在2001年提出的[11]。与随机森林类似, 梯度提升法也是一种组合算法, 其基分类器是决策树; 与随机森林不同之处在于, 它的每棵树是从先前所有树的残差中来学习的。
梯度提升法使用了梯度下降法, 正如其他梯度下降法一样, 如果步长太大, 优化过程就会发散而不收敛。但是梯度提升法会对预测值进行一系列的精确化, 沿着梯度下降的方向, 每走一步, 残差都会重新计算。在开始阶段, 梯度提升法将初始化预测值设为空(null)或零, 因此残差等于预测值。
3 滑动窗口残差统计法
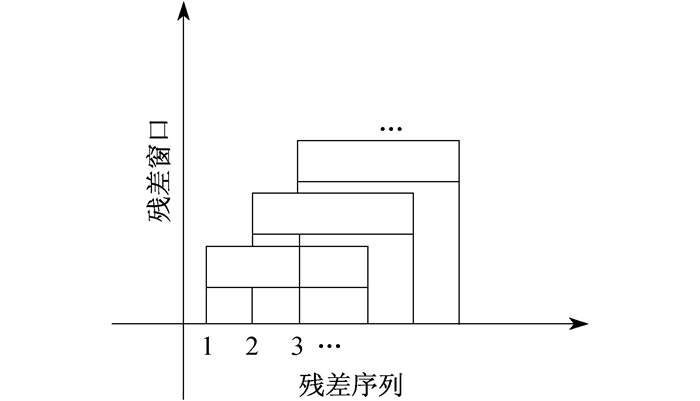
为了实时、连续地反映残差的分布变化, 采用滑动窗口法对残差均值和残差标准差进行统计分析, 结果示意如图 3所示。其中, 窗口的大小可以灵活选择[12]。与其他的统计法相比, 该统计法的优点主要有:算法易实现, 并且可以对新加入残差分布的变化进行统计分析; 合理地选择窗口大小能够确保统计的准确性和实时性; 在精度相同的情况下, 滑动窗口法能够给出发展性故障征兆的提示, 从而提高了预警的准确性和可靠性。
设极端随机树或随机森林所得到的参数预测值为
| $ \varepsilon=Y_{i}-\hat{Y}_{i} $ | (2) |
N个时刻构成的极限树模型残差序列为
| $ \varepsilon_{\mathrm{ET}}=\left[\begin{array}{lllll} \varepsilon_{1} & \varepsilon_{2} & \cdots & \varepsilon_{N} & \cdots \end{array}\right] $ | (3) |
对该序列取一个宽度为N的滑动窗口, N的取值主要结合经验选择。统计这个窗口内的残差均值为
| $ \bar \varepsilon = \frac{1}{N}\sum\limits_{i = 1}^N {{\varepsilon _i}} $ | (4) |
定义残差均值的故障预警阈值为E。设在N个窗口内残差均值绝对值的最大值为Emax, 即
| $ {E_{\max }} = \mathop {\max }\limits_{1 \le i \le N} \left| {\left\{ {{\varepsilon _1}\quad {\varepsilon _2}\quad \cdots \quad {\varepsilon _N}\quad \cdots } \right\}} \right| $ | (i) |
则定义燃烧室故障预警阈值为
| $ E=k E_{\max } $ | (6) |
式中:k——预警系数, 一般根据运行人员经验来确定, k < 1。
4 模型评价指标
均方根误差(RMSE)是用于衡量预测值与真实值之间的偏差, 均方误差(MSE)可表现预测值与真实值之间的差异程度, 平均绝对误差(MAE)反映了预测值误差的实际情况。本文采用上述指标对模型测试集的预测效果进行评价。
| $ {\rm{MSE}} = \frac{{\sum\limits_{i = 1}^S {{{\left( {{Y_i} - {{\hat Y}_{\rm{i}}}} \right)}^2}} }}{S} $ | (7) |
| $ {\rm{RMSE}} = \sqrt {\frac{{\sum\limits_{i = 1}^S {{{\left( {{Y_i} - {{\hat Y}_i}} \right)}^2}} }}{S}} $ | (8) |
| $ {\rm{MAE}} = \frac{1}{S}\sum\limits_{i = 1}^S {\left| {{Y_i} - {{\hat Y}_{\rm{i}}}} \right|} $ | (9) |
5 算法验证
某电厂于2018年5月6日某时刻1#机组跳闸, 再热蒸汽温度为487 ℃, 屏式再热器2#出口温度为564 ℃, 屏式再热器3#出口温度为568 ℃; 随后锅炉开始恢复启动, 再热蒸汽温度456 ℃, 屏式再热器2#出口温度为550 ℃, 屏式再热器3#出口温度为552 ℃。与启动前相比, 此时再热蒸汽处于欠温状态[13]。
5.1 自变量选择与样本数据集的构建
如前所述, 3种算法均以再热蒸汽出口温度为因变量, 其余变量为自变量, 因此选择与再热器出口温度相关的若干变量作为自变量, 用以预测再热器出口的真实温度。自变量的选取依据为再热器热平衡方程, 具体自变量如下:蒸汽进入再热器前的温度x1; 再热蒸汽压力x2; 烟道内温度x3; 烟道负压x4; 锅炉排烟温度x5。
自变量与因变量的数据来自SIS系统, 共收集到有效数据6 787组, 选取6 030组数据作为训练集, 757组故障隐患数据作为测试集, 采样间隔为1 min。
5.2 残差比较
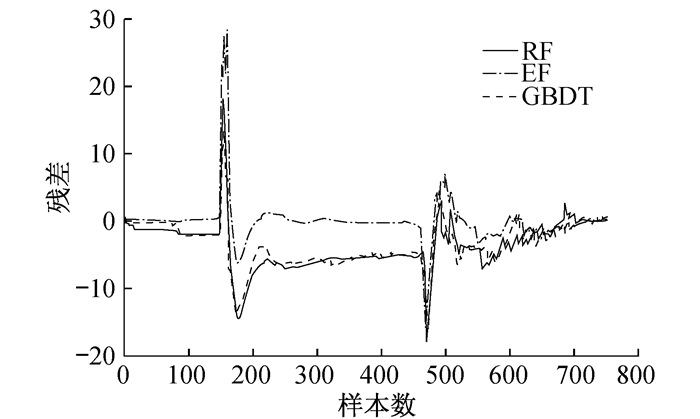
再热器出口温度预测值与真实值之间的残差可以间接反映再热器的运行状况:残差越大代表再热器与正常工况下运行的偏离程度越大。锅炉跳闸之前, 3种算法的再热器出口温度预测残差比较结果如图 4所示。
由图 4可以看出, 随机森林与梯度提升法的残差较为接近, 说明两种算法的再热器出口温度预测效果接近。在0~150 min和600~700 min时间段内, 3种算法的残差均接近于零, 此时再热器运行正常; 在150~600 min时间段内, 三者均有大幅度的振荡现象, 此时再热器出口温度的预测值偏离了实际值, 再热器欠温。在150 min时刻, 三者残差均有大幅度的跳跃, 极端随机树的残差跳跃程度大于其他两种算法, 说明极端随机树在预测排温时对再热器欠温隐患的放大程度大于其余两者。
记随机森林、极端随机树和梯度提升法的滑动窗口残差统计后的残差均值最大值分别为E1max, E2max, E3max, 选择故障预警系数k1=k2=k3=0.9, 计算出3种算法的预警阈值分别为E1=1.071, E2=0.297, E3=0.648。
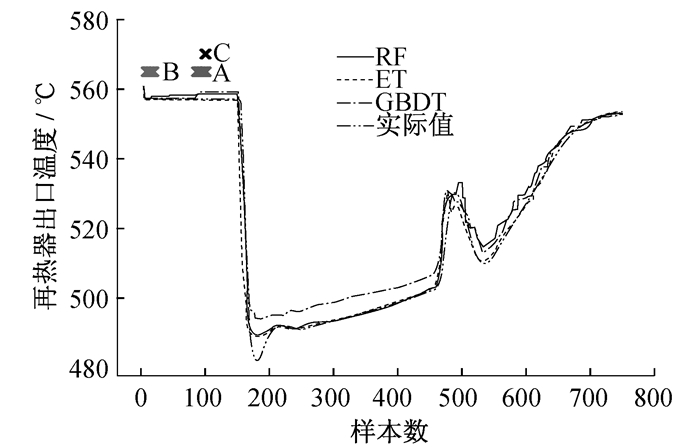
5.3 预警结果
图 5为3种算法的预警效果图。故障预警阈值为上文中的计算值。图 5中的A点、B点、C点分别代表随机森林、极端随机树和梯度提升法报警点, 运行人员可以直观地看到报警信息并及时处理。
3种算法的报警效果和预测误差如表 1所示。
表 1
3种算法报警效果和预测误差比较
| 算法 | 预警阈值 | 报警点个数 | 初始报警时刻/min | MSE | MAE | RMSE |
| RF | 1.071 | 17 | 82 | 7.331 | 1.699 | 2.708 |
| EF | 0.297 | 19 | 3 | 15.199 | 1.288 | 3.899 |
| GBDT | 0.648 | 2 | 95 | 18.285 | 3.378 | 4.276 |
由表 1可以看出, 与其他两种算法相比, 极端随机树的初始报警时刻最早, 比随机森林提前了79 min, 比梯度提升法提前了92 min, 说明极端随机树能够使运行人员更早地发现故障隐患。此外, 极端随机树报警点的个数为19, 比其他两种算法的预警点个数都要多, 且报警时间较长。MAE值可以较好地反映预测值误差的实际情况, 极端随机树的MAE值最小, 说明该算法对温度的预测效果最为准确。
6 结语
针对再热器欠温故障隐患问题, 建立了基于随机森林、极端随机树和梯度提升法的再热器出口温度预测模型, 并结合滑动窗口法计算3种算法的故障预警阈值。在计算得出温度预测值与真实值的残差后, 当残差超过预警阈值时发出报警信号, 提醒运行人员处理。实例分析结果表明, 与其他两种算法相比, 极端随机树在预测效果、报警时间和初时报警点等方面均有较大优势, 证明了该预警模型的有效性。
参考文献
-
[1]沈海华. 1 075 t/h锅炉再热器欠温改造方法[J]. 发电设备, 2016(1): 50-53.
-
[2]马加朋, 盖红德, 赵昆, 等. 电站锅炉过热器和再热器的失效模式及机理[J]. 山东工业技术, 2017(22): 13-14.
-
[3]刘鑫沛, 翟永杰, 张君颖, 等. 基于聚类分析和状态估计的制粉系统故障预警[J]. 计算机仿真, 2013, 30(8): 151-154.
-
[4]朱麟海.燃气轮机高温部件故障早期预警[D].哈尔滨: 哈尔滨工业大学, 2016.
-
[5]魏书荣, 何之倬, 唐征歧, 等. 海上风电机组的在线监测与故障预警[J]. 上海电力学院学报, 2014, 30(6): 569-573.
-
[6]黄伟, 张泽发. 基于相似度分析的电站燃气轮机燃烧室故障预警研究[J]. 上海电力学院学报, 2020, 36(3): 220-224.
-
[7]TAYARANI-BATHAIE S S, VANINI Z N S, KHORASANI K. Dynamic neural network-based fault diagnosis of gas turbine engines[J]. Neurocomputing, 2014, 125: 153-165. DOI:10.1016/j.neucom.2012.06.050
-
[8]SALAHSHOOR K, KORDESTANI M, KHOSHRO M S. Fault detection and diagnosis of an industrial steam turbine using fusion of SVM(support vector machine) and ANFIS (adaptive neuro-fuzzy inference system) classifies[J]. Energy, 2010, 130: 1-11.
-
[9]李欣海. 随机森林模型在分类与回归分析中的应用[J]. 应用昆虫学报, 2013, 50(4): 1190-1197.
-
[10]黄丛吾, 陈报章, 马超群, 等. 基于极端随机树方法的WRF-CMAQ-MOS模型研究[J]. 气象学报, 2018, 76(5): 119-129.
-
[11]万伦军.基于梯度提升模型的负相关学习算法的研究与应用[D].合肥: 中国科学技术大学, 2014.
-
[12]刘涛, 刘吉臻, 吕游, 等. 基于多元状态估计和偏离度的电厂风机故障预警[J]. 动力工程学报, 2016, 36(6): 455-456.
-
[13]刘福国, 赵万峰, 郭新根, 等. 低NOx燃烧器改造引起锅炉再热汽温降低的调整和改进[J]. 山东电力技术, 2015(5): 13-18.