|
|
|
发布时间: 2020-10-30 |
智能电网 |
|
|
|
收稿日期: 2020-05-11
基金项目: 国家自然科学基金(51977127)
中图法分类号: TM743
文献标识码: A
文章编号: 2096-8299(2020)05-0461-05
|
摘要
针对电力电缆行波定位法中难以准确检测含噪行波的问题,提出了一种基于差分和变换的电缆故障行波定位方法。对故障行波进行前后向差分运算,得到行波差分和信号,无需对行波信号进行降噪处理;利用奇异值分解和自适应阈值量化处理以滤除行波差分和信号中的背景噪声,从而准确检测故障行波的奇异值时刻;采用两端测距法实现电缆故障的精确在线定位。最后通过仿真模型验证了所提方法的有效性和优越性。
关键词
差分和变换; 行波定位; 奇异值分解; 两端测距
Abstract
In order to solve the problem that it is difficult to detect the noisy traveling-wave accurately in the fault location method of power cable, a traveling-wave location method based on difference summation transformation is proposed.The difference summation signal of traveling-wave can be obtained by the forward and backward difference operation of the fault traveling-wave without noise reduction.Singular value decomposition and adaptive threshold processing are used to filter out the background noise of the difference summation signal of traveling-wave, thereby accurately detect the singular value time of the fault traveling-wave.The method of two-terminal location can realize the accurate on-line location of power cable fault.Simulation results show the effectiveness and superiority of the proposed method.
Key words
difference summation transformation; traveling-wave location; singular value decomposition; two-terminal location
电力电缆因其安全、可靠、维护工作量小、通信容量大、使用寿命长、敷设方式美观等优点[1-3], 逐步在电力系统中得到了广泛应用, 特别在用电需求量大、供电质量要求高、交通拥堵的城市电网中, 电缆化程度得到不断提高[4]。虽然电力电缆较架空线故障几率低, 但因其一般埋于地下, 故障后位于盲区, 因此如何快速、准确、经济地定位电
缆故障, 对电缆线路运行维护、故障解除、保证电网持续可靠供电具有重要意义[2]。
现有电缆在线故障定位方法按原理可分为行波法[5]和阻抗法[6]。行波法因其不受故障类型、线路长度和过渡电阻等因素影响, 在电缆故障定位中得到了广泛应用[2]。行波法定位的关键是精确检测出行波的奇异点。目前常用的奇异点检测法有小波变换(Wavelet Transform, WT)、希尔伯特黄变换(Hibert-Huang Transform, HHT)和变分模态分解(Variational Mode Decomposition, VMD)等方法。WT的困难在于小波基函数选择且其会影响Lipschitz指数相同信号的奇异点检测效果, 从而影响定位精度[7]。HHT通过经验模态分解(Empirical Model Decomposition, EMD)将信号分为固有模态函数, 但EMD易造成模态混叠现象, 导致奇异点检测失败[8]。VMD虽克服了模态混叠, 但检测的奇异点位置在不同的分解层下会发生偏移[9]。此外, 电力电缆运行情况复杂, 且考虑到采集装置存在固有缺陷、传输通道易受外界环境干扰等因素, 因此实际采集的行波信号会不可避免地引入噪声, 会严重影响奇异点的检测。
基于上述背景, 本文提出了一种基于差分和变换(Difference Summation Transformation, DST)的电缆故障行波定位方法。首先, 分析了基于DST进行行波奇异点检测的基本原理; 然后, 介绍了利用奇异值分解(Singular Value Decomposition, SVD)降噪和阈值处理的奇异点检测过程; 最后, 通过仿真模型验证了所提方法的有效性和优越性。
1 差分和变换行波检测法
1.1 DST基本原理
考虑到电缆故障时三相暂态参数存在耦合, 采用Karenbauer变换对其进行解耦运算, 得到线模和地模的分量信号。本文采用衰减系数小、波速近似恒定的线模信号进行奇异点检测。故障定位的关键步骤是精确检测出线模行波信号(下文统称行波信号)L的奇异点, 利用DST可以精确定位L的奇异点时刻。
差分的实质是对离散信号进行微分运算, 分为前向差分
| $ D(i)=\left\{\begin{array}{ll} L(i)-L(i+1) & i=1 \\ L(i)-L(i-1) & i=N \\ \sum\limits_{r=1}^{R}[L(i)-L(i-r)+ \\ L(i)-L(i+r)] & \text { 其他 } \end{array}\right. $ | (1) |
当2≤i≤N-1时, R满足
| $ R=\left\{\begin{array}{lc} i-1 & 2 \leqslant i \leqslant h \\ h & h<i<N-h \\ N-i & N-h<i \leqslant N-1 \end{array}\right. $ | (2) |
式中:L(i)——故障行波信号采样数据, i=1, 2, 3, …, N, N为采样点数;
R——以某一时刻为中心的最大差分半径;
h——局部分析窗的宽度。
在某一局部分析窗h内非故障信号是连续且存在一阶导数的, 由式(1)可知其差分和为零; 而对于故障信号L, 其差分和不为零, 且奇异点差分和值随h的增大而增大。由此, 可以定位出奇异点的位置。
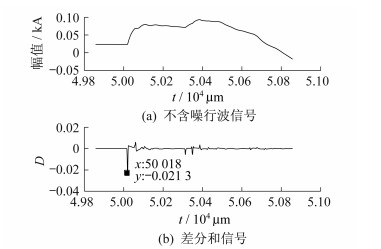
图 1为一不含噪故障行波信号及其对应的差分和信号, 故障时间为50 018 μs。由图 1(b)可知, 故障行波信号基于DST后首波奇异点位置检测准确且奇异点数目也正确。
1.2 SVD降噪
故障行波信号L经DST后, 虽然可从差分和信号D中定位奇异点, 但受外界环境干扰, 实际采集的信号L将不可避免地引入噪声, 故D中的背景噪声会影响检测器的精度。为进一步突出D中奇异点的特征峰, 采用SVD对其进行降噪处理, 基本步骤如下。
步骤1 对一维时间序列差分和信号D进行3行Hankel矩阵变换, 得到矩阵D′。
步骤2 对D′做奇异值分解。
| $ \boldsymbol{D}^{\prime}=\boldsymbol{U} \boldsymbol{S} \boldsymbol{V}^{\mathrm{T}} $ | (3) |
式中:U——左正交矩阵, U=(u1, u2, u3);
V——右正交矩阵, V=(v1, v2, …, vN-2);
S=(diag(λ1, λ2, λ3), O), 且λ1≥λ2≥λ3≥0, 均为特征值, O为零矩阵。
步骤3 令D′1=λ1u1v1T, D′2=λ2u2v2T, D′3=λ3u3v3T, 替换D′。
由SVD分解性质可得
| $ \boldsymbol{D}^{\prime}=\boldsymbol{D}_{1}^{\prime}+\boldsymbol{D}_{2}^{\prime}+\boldsymbol{D}_{3}^{\prime} $ | (4) |
对于奇异信号和噪声信号, 矩阵D′呈现不同的特征:对于奇异信号, D′各行高度相关且满足
步骤4 对D′1做反Hankel变换, 以获取降噪后的差分和信号D。
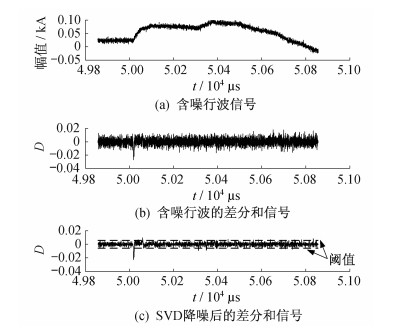
为验证基于SVD降噪的有效性, 对图 1所示的不含噪故障行波信号添加一白噪声信号, 其信噪比为30 dB, 如图 2(a)所示。对其进行差分和变换后, 得到的差分和信号如图 2(b)所示, 可见虽然差分和信号中的信噪比低于30 dB, 但却依然出现了奇异点的特征峰值。经过SVD降噪后的差分和信号如图 2(c)所示, 可见其背景噪声大大减小, 奇异点特征峰值更加明显, 验证了SVD降噪的有效性。
1.3 模极大值提取
采用通用阈值法对差分和信号D进行阈值量化处理, 即
| $ \xi=\operatorname{median}(|D|) \frac{\sqrt{2 \log N}}{0.6745} $ | (5) |
| $ \begin{array}{l} D(i)=\left\{\begin{array}{ll} D(i) & |D(i)|>\xi \\ 0 & |D(i)| \leqslant \xi \end{array}\right. \end{array} $ | (6) |
式中:ξ——选取的阈值;
median(·)——计算中值。
量化后差分和信号D中第一个模极大值点就是首波的奇异值点位置, 如图 3所示。由图 3可见, 经过阈值量化后的差分和信号首波奇异点的位置清晰可见。
2 双端行波定位
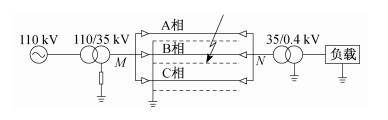
时间监测点分别位于电缆M和N两端, 采用GPS时间同步装置, 由图 4可得测距公式为
| $ \left\{\begin{array}{l} L_{M F}=\frac{v\left(t_{M}-t_{N}\right)+L_{\mathrm{T}}}{2} \\ L_{N F}=\frac{v\left(t_{N}-t_{M}\right)+L_{\mathrm{T}}}{2} \end{array}\right. $ | (7) |
式中:LMF, LNF——故障点F距离M端和N端的长度;
v——行波波速;
tM, tN——故障初始行波到达M端和N端所用的时间;
LT——线缆的总长度, 即M和N两点间的距离。
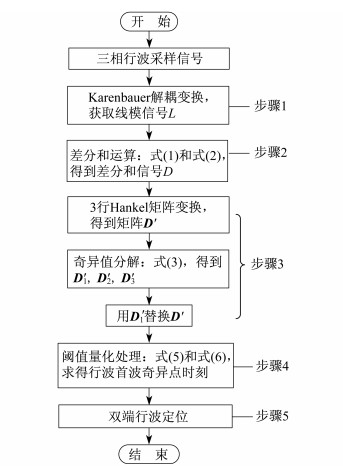
综上所述, 基于差分和变换的电缆故障行波定位方法基本流程如图 5所示。
3 仿真案例分析
3.1 仿真模型
3.2 故障行波检测
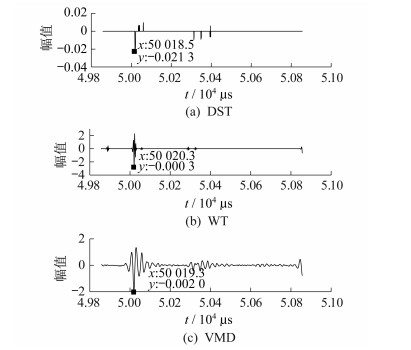
为验证所提DST方法相比WT和VMD的优越性, 对图 1所示的故障行波信号, 即为图 5距离M端2 km处发生A相单相接地故障时M点检测器采集的信号, 添加信噪比为30 dB的白噪声。WT和VMD需要对含噪故障行波信号进行前置滤噪, 本文采用小波阈值法[12]。3种方法对该行波信号的奇异点检测结果如图 7所示。
故障点理想时刻为50 018 μs。由图 7可知, DST, WT, VMD检测出的奇异点首波时刻分别为50 018.5 μs, 50 020.3 μs, 50 019.3 μs, 误差值分别为0.5 μs, 2.3 μs, 1.3 μs。可见本文所提方法较WT和VMD具有较强的抗噪能力, 且精度较高。
3.3 仿真结果
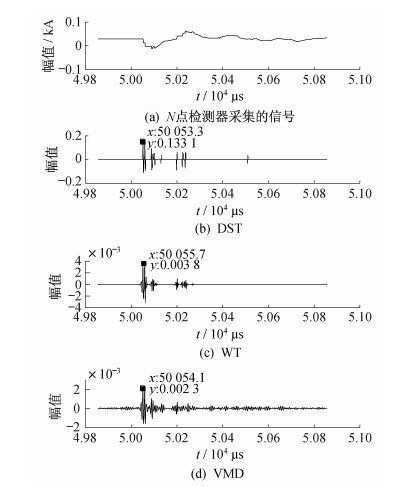
上述已经得到在距离M端2 km处发生A相单相接地故障时M点检测器采集信号的首波奇异点时刻, 为实现故障定位, 对N点检测器采集的信号也添加信噪比为30 dB的白噪声。3种方法对该行波信号的奇异点检测结果如图 8所示。
由图 8可知, DST, WT, VMD检测出的奇异点首波时刻为50 053.3 μs, 50 055.7 μs, 50 054.1 μs, 结合上述M点检测出的奇异点首波时刻, 代入式(7), 计算得故障定位结果和误差如表 1所示。
表 1
单相接地故障时3种方法的故障定位结果
| 方法 | 端点 | 首波时刻/μs | 定位结果/km | 误差/km |
| DST | M | 50 018.5 | 2.021 | 0.021 |
| N | 50 053.3 | |||
| WT | M | 50 020.3 | 1.973 | 0.027 |
| N | 50 055.7 | |||
| VMD | M | 50 019.3 | 2.023 | 0.023 |
| N | 50 054.1 |
为进一步验证本文所提方法的有效性和优越性, 分别在图 6距离M点2 km, 5 km, 7 km处设置不同的故障类型, 且同样在采集的故障行波信号中添加信噪比为30 dB的白噪声, 采用两端测距法, 3种方法的定位结果和相对误差如表 2所示。表 2中, AG, AB, ABC分别表示单相接地、两相短路和三相短路故障。
表 2
3种方法故障定位结果
| 故障位置/km | 故障类型 | 定位结果/km | 相对误差/% | |||||
| DST | WT | VMD | DST | WT | VMD | |||
| 2 | AG | 2.021 | 1.973 | 2.023 | 1.07 | 1.34 | 1.13 | |
| AB | 2.027 | 2.020 | 2.024 | 1.34 | 0.99 | 1.19 | ||
| ABC | 2.022 | 2.026 | 2.023 | 1.09 | 1.30 | 1.15 | ||
| 5 | AG | 4.951 | 4.940 | 5.057 | 0.97 | 1.20 | 1.15 | |
| AB | 4.946 | 5.063 | 5.057 | 1.08 | 1.26 | 1.13 | ||
| ABC | 4.961 | 5.049 | 5.041 | 0.78 | 0.97 | 0.81 | ||
| 7 | AG | 7.049 | 7.060 | 6.948 | 0.70 | 0.86 | 0.74 | |
| AB | 7.065 | 7.077 | 6.915 | 0.93 | 1.09 | 1.22 | ||
| ABC | 7.061 | 7.066 | 6.918 | 0.87 | 0.94 | 1.17 | ||
由表 2可知, 采取本文方法仅在距离M端2 km处发生两相短路时相对误差较WT和VMD大, 其余情况下均较其他两种方法小。由此可见, 与WT和VMD相比, 本文所提方法精度高且定位误差满足实际工程需求。
4 结语
本文提出了一种基于差分和变换的故障行波定位方法, 可以准确检测首波的奇异点时刻, 通过奇异值分解和阈值量化处理, 可使奇异点特征峰值更加明显。仿真结果表明, 相比于小波变换和变分模态分解, 本文提出的方法具有较强的抗噪能力且定位精度较高, 可以满足实际工程需要。
参考文献
-
[1]唐进, 张姝, 林圣, 等. 计及金属护层结构的电缆单端故障测距方法[J]. 中国电机工程学报, 2016, 36(6): 1748-1756.
-
[2]张姝, 林圣, 唐进, 等. 基于双层阻抗模型的三相单芯电缆自恢复故障定位[J]. 电工技术学报, 2016, 31(17): 1-10.
-
[3]LAN S, HU Y, KUO C. Partial discharge location of power cables based on an improved phase difference method[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2019, 26(5): 1612-1619. DOI:10.1109/TDEI.2019.008202
-
[4]王国昊, 姜玉林, 宋云峰, 等. 基于行波测距技术的电缆故障定位的应用[J]. 东北电力技术, 2020, 41(2): 16-18.
-
[5]廖晓辉, 赵肖健, 梁恒娜. 一种基于Hilbert-Huang变换的电力电缆故障测距方法[J]. 电力系统保护与控制, 2017, 45(3): 20-25.
-
[6]姜杰, 王鹏, 黄正炫, 等. 基于改进线路参数模型的配网电缆单相接地测距方法[J]. 电网技术, 2012, 36(5): 185-189.
-
[7]唐炬, 董玉林, 樊雷, 等. 基于Hankel矩阵的复小波-奇异值分解法提取局部放电特征信息[J]. 中国电机工程学报, 2015, 35(7): 1808-1817.
-
[8]徐俊明, 汪芳宗, 尹星, 等. 基于Hilbert-Huang变换的行波法高压输电线路故障定位[J]. 电力系统保护与控制, 2012, 40(2): 88-92.
-
[9]高艳丰, 朱永利, 闫红艳, 等. 基于VMD和TEO的高压输电线路雷击故障测距研究[J]. 电工技术学报, 2016, 31(1): 24-33.
-
[10]张岚, 王献军, 赵卫华. 电力电缆故障定位在线检测研究[J]. 电气技术, 2018, 19(10): 55-58.
-
[11]赵铁军, 王秀斌, 虞跃. 基于金属护层模型参数辨识的电缆单相故障单端测距方法[J]. 电力系统保护与控制, 2019, 47(21): 83-91.
-
[12]赵坤, 郑小霞. 基于改进EMD和小波阈值法的风机数据降噪研究[J]. 上海电力大学学报, 2020, 36(2): 136-140.