|
|
|
发布时间: 2020-10-25 |
智能电网 |
|
|
|
收稿日期: 2020-07-14
基金项目: 国网河南省电力公司科技项目(521750200017)
中图法分类号: TM71
文献标识码: A
文章编号: 2096-8299(2020)05-0471-06
|
摘要
目前部分供电公司对台区的线损管理仍采取人工方式,通过对比供售电量并按照预定的阈值对台区进行线损率异常判断。该方法计算精度较低并且不能充分考虑不同台区的线损水平差异,有一定的局限性。为此,提出了基于边缘计算模式的台区线损率计算方法,结合边缘计算模式以及相关技术,将配电台区作为边缘计算节点,采用近邻传播(AP)算法对台区电气特征参数进行分类,并通过LM算法优化的BP神经网络模型对低压台区线损率进行计算,判断该台区是否存在异常。
关键词
边缘计算; 近邻传播算法; BP神经网络; 台区线损率
Abstract
At present, some power supply companies still adopt a manual method for the line loss management of the station area.By comparing the supply and sales of electricity and making an abnormal judgment of the line loss rate of the station area according to a predetermined threshold, this method has low calculation accuracy and cannot fully consider the different line loss levels.Therefore, a line loss rate calculation method for the station area based on the edge calculation mode is proposed.This method combines the edge calculation mode and related technologies, makes the power distribution station area as the edge calculation node, and uses the Affinity Propagation to classify the electrical characteristics of the station area.The BP neural network model optimized by the LM algorithm is used to calculate the line loss rate of the low-voltage station area to determine whether there is abnormality in the station area.
Key words
edge caculation; affinity propagation; BP neural network; transformer line loss
随着通信技术以及互联网技术等的不断进步[1-3], 配电网将向着信息流、电力流、能源流高度融合的开放、智能、柔性、清洁的新型运行模式持续发展[4]。国家电网公司在2019年提出了建设全面状态感知、信息高效处理的“泛在电力物联网”[5]。然而海量的电力数据涌入使得传统的云计算模型无法高效地处理电力数据, 边缘计算模式的出现巧妙地解决了这一问题。边缘计算将计算分析功能扩展至网络边缘具备一定计算能力的设备, 就近处理电力数据, 仅需返回结果至云中心, 缓解了云中心的数据处理压力。
台区作为电力物联网的关键组成部分, 更靠近用户端, 因此台区更适合作为边缘计算模式的边缘节点, 在台区内就地分析处理数据[6-7], 有助于推动泛在电力物联网建设。台区线损管理又是台区管理中的关键组成部分[8], 因此使用合理的方法对台区线损率进行管理极为重要。
目前部分供电公司对台区的线损管理仍采取人工方式, 通过对比供电量以及售电量并按照预定的阈值对台区进行线损率异常判断, 但费时费力、计算精度较低并存在一定的片面性, 忽略了不同台区的线损水平差异, 不能合理地对台区线损率进行判断。部分学者以负荷为基础对台区线损率进行了理论计算[9-10], 也有部分学者将线性回归算法[11-12]运用在台区线损计算中。但是, 以上几种方法计算准确度较低且工作量大, 无法就地进行台区线损率计算, 大量耗费人力、物力和财力。
本文提出了一种基于边缘计算, 模式的台区线损率计算方法, 可以在边缘端就地进行台区线损率计算, 以缓解云中心的处理压力。首先, 构建了台区电气特征指标体系; 其次, 采用近邻传播算法(Affinity Propagation, AP)对其进行分类, 在此基础上建立了LM算法(Levenberg-Marquardt)优化的反向传播(Back Propagation, BP)神经网络模型, 并在云中心对其进行训练优化; 最后, 将模型移植到边缘物联代理中, 对台区的线损率进行预测计算。经仿真实验验证, 本文所提方法具有一定的实用性和有效性。
1 基于边缘计算模式的台区结构
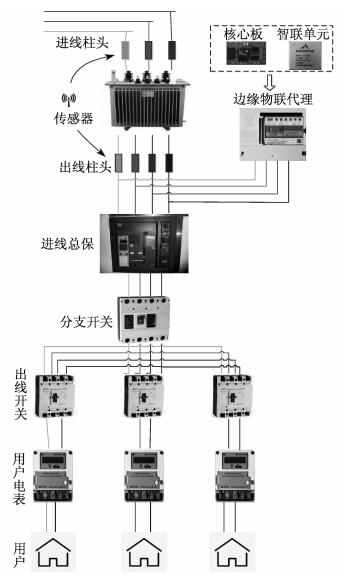
台区指(1台)变压器的供电范围或区域, 主要由母线、熔断器、配电变压器、开关、电表等部分组成。由于传统台区的计算力较弱, 不足以支持边缘计算模式, 无法实现对线损的精益化计算和分析、电能质量分析及治理、台区综合能源协同控制等功能, 因此需要对台区进行升级改造。除了在台区中加装智能开关、智能传感器以及智能电表之外, 最关键的是需要加装智能配变终端(即边缘物联代理)。边缘物联代理是配电台区进行用电信息采集、设备状态监测及通信组网、就地化分析决策、主站通信及协同计算等功能于一体的智能化终端设备。
边缘物联代理采用“硬件平台化, 软件APP化”的设计理念, 以标准化、模块化的硬件设计与低成本的软件APP方式, 在配电台区中作为数据汇聚、边缘计算、应用集成的中心, 边缘物联代理应部署在配变出线侧, 如图 1所示。
边缘物联代理由核心板和智联单元(物联网通信单元等)构成, 监控配电变压器至用户智能电表间的运行数据, 天然具备边缘计算节点特性, 所以是配电台区管理架构的核心。
2 基于边缘计算的台区线损率计算方法
2.1 台区电气特征指标体系建立
由于各个台区所处地域地形、负荷结构和电网建设程度的不同, 大致可以把台区划分为城市、郊区和农村3类台区[13], 其中城市台区、郊区和农村台区的用电量、负荷密度、供电半径均存在差异。为了充分利用台区内电气特征参数, 挖掘出信息的价值, 需要对台区内电气特征参数进行预处理。
考虑到电气特征参数的易获取性和可行性[14], 选取以下3种参数作为台区电气特征指标。其中, 反映网架特征的指标即线路特征参数有供电半径和最大供电长度, 反映负荷特性的指标即变压器特征参数有配变负载率[15]。
(1) X1, 供电半径(m), 指台区变压器到供电范围内用户端的距离。该指标是评估低压配电网台区网架结构是否合理的重要参数之一。
(2) X2, 最大供电长度(m), 指该台区实际最大供电长度。
(3) X3, 配变负载率(%), 是指台区内供电量与变压器的额定容量之比, 反映了当前台区变压器的负载状况以及台区内负荷的平均水平。
由于上述选取的3项指标的单位与性质各不相同, 数值间的差别较大, 不进行处理可能会影响训练模型数据分析的结果, 因此需要对原始数据进行标准化处理, 消去指标之间量纲和取值范围差异的影响。设特征参数个数为m个, 样本数为N个。其处理方法如下。
| $ {Z_{ij}} = \frac{{{x_{ij}} - \overline {{x_j}} }}{{\sqrt {{S_{ij}}} }} $ | (1) |
| $ \overline {{x_j}} = \frac{1}{N}\sum\limits_{i = 1}^N {{x_j}} $ | (2) |
| $ {S_{ij}} = \frac{1}{{N - 1}}\sum\limits_{i = 1}^N {{{({x_{ij}} - \overline {{x_j}} )}^2}} $ | (3) |
式中:Zij——xij标准化处理后的量;
xij——第i个台区第j个参数;
Sij——xij的方差。
2.2 AP聚类算法模型
为了更好地挖掘出台区电气特征参数的潜在信息, 需要筛选出用电性质相同的台区, 因此本文选用聚类精度较高的AP聚类算法。AP聚类算法是一种基于数据点之间的“信息传递”的聚类算法[16], 根据N个数据点之间的相似度进行聚类, 用吸引度矩阵R和归属度矩阵A在数据点之间交换信息, 不断迭代更新两个信息矩阵, 直到迭代结束。其公式为
| $ {\rm{ }}{{r}_{t + 1}} = \left\{ \begin{array}{l} S\left( {i, k} \right) - \mathop {\rm max}\limits_{j \ne k} \{ {{a}_t}\left( {i, j} \right) + {{r}_t}\left( {i, j} \right)\} , \\ i \ne k\\ S\left( {i, k} \right) - \mathop {\rm max}\limits_{j \ne k} \left\{ {S\left( {i, j} \right)} \right\}, i = k \end{array} \right. $ | (4) |
| $ {{a}_{t + 1}}(i,k) = \left\{ \begin{array}{l} {\rm min}\{ 0,{{r}_{t + 1}}(k,k) + \\ {\mathit{\boldsymbol{\sum\limits}}}_{j \ne i,k} {{\rm max}\{ {{r}_{t + 1}}(j,k),0\} \} ,i \ne k} \\ {\mathit{\boldsymbol{\sum\limits}}}_{j \ne k} {{\rm max}\{ {{r}_{t + 1}}(j,k),0\} ,i = k} \end{array} \right. $ | (5) |
式中:r(i, j), a(i, j)——i点与j点之间的吸引度矩阵和归属度矩阵;
S(i, j)——i点与j点之间的相似度。
r(i, j)与a(i, j)的值越大, 则j点作为聚类中心的可能性就越大, 并且i点隶属于以j点为聚类中心的类簇的可能性也越大。
由于AP聚类算法的迭代过程容易产生振荡, 所以每次迭代都要加上一个阻尼系数λ, λ∈(0, 1), 则有
| $ {{r}_{i + 1}}\left( {i, j} \right) ={\lambda }\cdot{{r}_i}\left( {i, j} \right) + \left( {1 - {\mathit{\boldsymbol{\lambda}}} } \right)\cdot{r}_{_{i + 1}}^{^{{\rm old}}}\left( {i, j} \right) $ | (6) |
| $ {{a}_{i + 1}}\left( {i, j} \right) ={\lambda} \cdot{{a}_i}\left( {i, j} \right) + \left( {1 - {\mathit{\boldsymbol{\lambda}}} } \right)\cdot{a}_{_{i + 1}}^{^{{\rm old}}}\left( {i, j} \right) $ | (7) |
式中:
该算法流程如下。
(1) 更新相似度矩阵中每个点的吸引度信息, 计算归属度信息;
(2) 更新归属度信息, 计算吸引度信息;
(3) 对样本点的吸引度信息和归属度信息求和, 检测其选择聚类中心的决策。
若经过若干次迭代之后其聚类中心不变, 或者迭代次数超过既定的次数, 又或者一个子区域内的关于样本点的决策经过数次迭代后保持不变, 则算法结束。
相比传统聚类算法, AP聚类算法的主要优点如下:一是算法不需要制定最终类簇的个数; 二是将已有的数据点作为最终的聚类中心, 而不是新生成一个簇中心; 三是模型对数据的初始值不敏感; 四是对初始相似度矩阵数据的对称性没有要求; 五是其结果的平方差误差更小, 聚类精度较高。
AP聚类算法每次迭代都需要更新每个数据点的吸引度值和归属度值, 在大数据量下运行时间较长, 因此在以往的研究中较少使用。边缘计算模式的出现解决了这一问题。边缘计算将主站的功能移植至边缘端中, 就地对台区数据进行处理, 仅需要返回计算结果至主站, 并不需要频繁地访问主站数据库。
2.3 LM算法优化的BP神经网络模型
2.3.1 标准BP神经网络模型
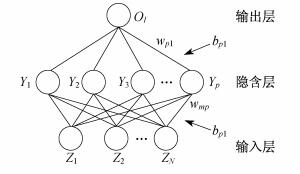
BP神经网络是目前应用最广泛、最成功的神经网络模型之一。其学习规则是使用最速下降法, 通过反向传播来不断调整网络的权值和阈值[17], 使网络的误差平方和最小。BP神经网络模型结构如图 2所示。
对于任意一台区, 设台区的电气特征参数为N个, 因此神经网络的输入层有N个BP神经元输入。设输入层的输入向量为
利用BP神经网络模型对Zij和di进行学习训练的正向传播过程为
| $ {Y_p} = f(\sum\limits_{n = 1}^N {({w_{np}}{Z_N} + {b_{np}}))} $ | (8) |
| $ {O_l} = f(\sum\limits_{p = 1}^P {({w_{pl}}{Y_P} + {b_{pl}})} ) $ | (9) |
式中:wnp, bnp——输入层到隐含层的权值和阈值;
wpl, bpl——隐含层到输出层的权值和阈值。
输出误差e为
| $ e = \frac{1}{2}\sum\limits_{l = 1}^L {{{({d_l} - {O_l})}^2}} $ | (10) |
当实际输出与期望输出不符时, 进入误差的反向传播阶段。误差通过输出层, 按误差梯度下降的方式修正各层权值, 向隐含层、输入层逐层反传。权值调整过程一直进行至网络输出的误差减少到可以接受的程度, 或者预先设定的学习次数为止。
2.3.2 LM算法优化的BP神经网络模型
LM算法是使用最广泛的非线性最小二乘算法, 用模型函数对待估参数向量在其领域内做线性近似, 利用泰勒展开, 忽略掉二阶以上的导数项, 可以将优化目标方程转化为线性最小二乘问题。该算法在优化神经网络训练均方误差方面具有较强的适用性。本文以权值修正过程为例进行介绍[18]。
在第n+1次的迭代过程中, 误差e按泰勒公式展开, 得到的公式[18]为
| $ \begin{array}{l} e\left( {w\left( {n + 1} \right)} \right) = e\left( {w\left( n \right)} \right) + {g^{\rm{T}}}\left( n \right)\Delta w\left( n \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{0.5^{\rm{T}}}\Delta w\left( n \right){A}\left( n \right)\Delta w\left( n \right) \end{array} $ | (11) |
式中:w(n)——第n次迭代过程中的权值;
A(n)——Hessian矩阵。
式(11)中, 当Δw(n)=-A-1(n)g(n)时, e(w(n+1))取得最小值。
采用LM算法对BP神经网络进行优化, 将A(n)表示为
| $ {A}\left( n \right) = {{J}^{\rm{T}}}{J} $ | (12) |
式中:J——雅克比矩阵。
LM算法对权值和阈值的修正公式为
| $ w\left( {n + 1} \right) = w\left( n \right) - {[{{J}^{\rm{T}}}{J} + \mu {I}]^{ - 1}}{{J}^{\rm{T}}}e $ | (13) |
| $ b\left( {n + 1} \right) = b\left( n \right) - {[{{J}^{\rm{T}}}{J} + \mu {I}]^{ - 1}}{{J}^{\rm{T}}}e $ | (14) |
式中:I——单位向量;
μ——常数;
b(n)——第n次迭代过程中的阈值。
LM算法不仅具有高斯-牛顿算法的局部收敛性, 而且还具有梯度下降法的全局特性。应用LM算法对BP神经网络进行优化, 与其他的BP神经网络优化方法相比, 能够很有效地降低网络权值的数目, 节省训练时间, 使网络迅速收敛且训练误差最小, 满足边缘计算模式的实时性要求, 能够较好地在边缘计算模式中得到运用。
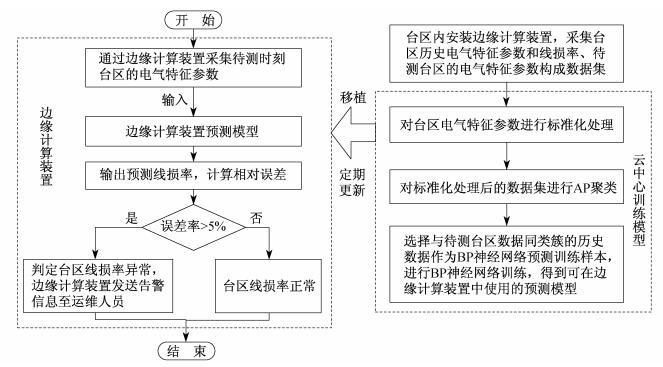
2.4 基于边缘计算的台区线损率计算流程
基于边缘计算模式的台区线损率计算方法, 主要包括以下几个步骤。
(1) 在台区内安装边缘计算装置, 利用边缘计算装置采集不同台区某历史时间段不同时刻的电气特征参数和线损率作为历史数据, 通过边缘计算装置采集待测台区待测时刻的电气特征参数。
(2) 对台区电气特征参数进行标准化处理。
(3) 通过AP聚类算法对台区的电气特征参数数据进行聚类, 计算数据之间的相似度并设置阻尼系数, 得到多个类簇。
(4) 选取与待测时刻的电气特征参数同一类簇的历史数据作为云平台预测模型的训练样本数据集, 在云平台内通过BP神经网络对数据集进行训练, 得到台区线损率预测模型。
(5) 将训练完成的预测模型移植到边缘计算终端设备, 并通过边缘终端设备采集台区待测时刻的电气特征参数, 通过模型进行预测, 得出实时预测的线损率。
(6) 将预测出的实时线损率与该台区的理论线损率进行对比, 计算误差率。误差率大于5%时则判定该台区线损率异常, 然后通过边缘计算装置发送告警信息至运维人员。
(7) 通过采集的台区历史数据, 在云平台对预测模型进行深入训练, 并定期对边缘设备的预测模型进行更新, 保证边缘计算设备预测模型的准确率。
台区线损率计算流程如图 3所示。
3 算例分析及验证
为了验证本方法的有效性, 选取某地区的台区电气特征参数进行仿真, 并对台区的线损率进行计算。某地区的10个台区的电气特征参数如表 1所示。
表 1
10个台区的电气特征参数表
| 台区 | 供电量/ kWh | 售电量/ kWh | 供电半径/ m | 最大供电长度/m | 配变负载率/% |
| 1 | 136 795 | 128 954 | 216 | 467 | 42.69 |
| 2 | 145 987 | 136 541 | 256 | 496 | 59.37 |
| 3 | 168 975 | 158 562 | 189 | 453 | 65.31 |
| 4 | 123 689 | 115 659 | 201 | 498 | 43.56 |
| 5 | 289 623 | 278 964 | 236 | 560 | 40.28 |
| 6 | 375 698 | 365 987 | 209 | 598 | 39.65 |
| 7 | 445 698 | 432 139 | 266 | 689 | 55.23 |
| 8 | 597 856 | 572 364 | 279 | 716 | 49.56 |
| 9 | 372 698 | 362 326 | 159 | 421 | 70.26 |
| 10 | 678 954 | 639 627 | 298 | 856 | 50.26 |
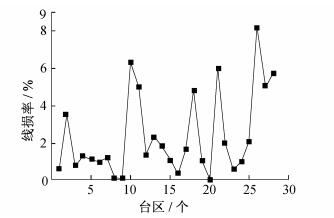
对供电量和售电量进行计算, 可得出该地区台区的实际线损率(即理论线损率)。为了体现不同台区的线损率差异, 选取了该地区28个台区的供售电量进行计算。该地区28个台区的实际线损率如图 4所示。
由图 4可以看出, 各个台区线损率水平参差不齐, 难以用统一的标准去衡量台区的线损率, 并且台区是否存在异常难以判断。因此本文在边缘计算模式下, 首先对台区数据进行聚类预处理, 然后用LM算法优化的BP神经网络对台区线损率进行预测, 并比较预测线损率与实际线损率, 计算其误差率并将计算结果传输至云中心。若误差率大于5%则判定该台区异常, 并通过边缘物联代理将告警信息发送至运维人员。
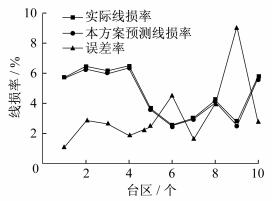
将预测出的实时线损率与该台区的理论线损率进行对比, 计算误差率, 结果如图 5所示。
由图 5可以看出, 实际线损率与本方案计算出来的预测线损率相对误差较小, 因此本方案可实现对台区实际线损率的预测, 体现了本文所提方法的有效性。此外, 从图 5可以看出, 大部分台区的实际线损率与预测线损率的误差率小于5%, 处于正常运行状态; 当实际线损率与预测线损率的误差率大于5%时, 则认为该台区异常, 需要通过人工核实该台区是否存在窃电、漏电等造成线损率异常的行为。
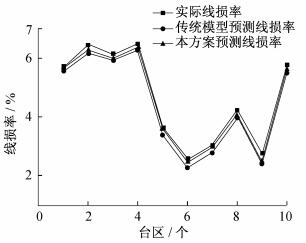
为了进一步验证本方法的优越性, 构建了传统BP神经网络模型, 并与本文方法相比较, 结果如图 6所示。
由图 6可知, 传统BP神经网络模型的预测值、本方案预测模型的预测值与实际线损率相比都很接近, 均可实现对线损率的预测。传统BP神经网络模型误差在10-2数量级, LM算法优化的BP神经网络模型误差10-5数量级, 因此可相比传统预测模型所得的台区线损率预测结果精度更高, 并且在边缘计算模式下, 可定期对边缘计算装置中的预测模型进行优化更新, 预测精度较高, 具有实际运用价值。通过本方法的实施应用, 可以节省大量的人力、物力和财力, 促进了国家电网公司泛在电力物联网的建设。
4 结语
本文将台区作为边缘边缘计算节点, 并给出了基于边缘计算模式的台区技术架构, 提出了一种在台区运用的基于边缘计算模式的线损率计算方法。本方法可就地化计算台区线损率并辅助运维人员对台区作维护, 但是本方法无法挖掘出使得台区线损率异常的原因, 需要相关学者作进一步的探究。
参考文献
-
[1]王玮, 李睿, 姜久春. 面向能源互联网的配电系统规划关键问题研究综述与展望[J]. 高电压技术, 2016, 42(7): 2028-2036.
-
[2]刘国军, 侯兴哲, 王楠, 等. 智能配用电通信综合网管系统研究[J]. 电网技术, 2012, 36(1): 12-17.
-
[3]孙宏斌, 郭庆来, 潘昭光. 能源互联网:理念、架构与前沿展望[J]. 电力系统自动化, 2015, 39(19): 1-8.
-
[4]田世明, 栾文鹏, 张东霞, 等. 能源互联网技术形态与关键技术[J]. 中国电机工程学报, 2015, 35(14): 3482-3494.
-
[5]国家电网公司.泛在电力物联网建设大纲[EB/OL].(2019-03-11)[2019-05-28].http://www.chinasmartgrid.com.cn/news/20190311/632172.shtml.
-
[6]吕军, 栾文鹏, 刘日亮, 等. 基于全面感知和软件定义的配电物联网体系架构[J]. 电网技术, 2018, 42(10): 3108-3115.
-
[7]孙浩洋, 张冀川, 王鹏, 等. 面向配电物联网的边缘计算技术[J]. 电网技术, 2019, 43(12): 4314-4321.
-
[8]杨欢红, 岑雅, 温杰, 等. 电网配电线路的线损分析系统设计[J]. 上海电力学院学报, 2015, 31(1): 35-38.
-
[9]张恺凯, 杨秀媛, 卜从容, 等. 基于负荷实测的配电网理论线损分析及降损对策[J]. 中国电机工程学报, 2013, 33(增刊): 92-97.
-
[10]刘庭磊, 王韶, 张知, 等. 采用负荷电量计算低压配电台区理论线损的牛拉法[J]. 电力系统保护与控制, 2015, 43(19): 143-148.
-
[11]邹云峰, 梅飞, 李悦, 等. 基于数据挖掘技术的台区合理线损预测模型研究[J]. 电力需求侧管理, 2015, 4(17): 25-29.
-
[12]杨秀台. 电力网线损的理论计算和分析[M]. 北京: 水利电力出版社, 1985: 135-214.
-
[13]欧阳森, 陈欣晖. 考虑基态-差异化特征的台区无功优化配置策略[J]. 电网技术, 2015, 39(12): 3513-3519.
-
[14]欧阳森, 杨家豪, 耿红杰, 等. 面向台区管理的台区状态综合评价方法及其应用[J]. 电力系统自动化, 2015, 39(11): 187-192.
-
[15]马纪, 刘希喆. 基于G_2-熵权法的低压配网台区状态特性评估[J]. 电力自动化设备, 2017, 37(1): 41-46.
-
[16]王知芳, 杨秀, 潘爱强, 等. 基于改进集成聚类和BP神经网络的电压偏差预测[J]. 电工电能新技术, 2018, 37(5): 73-80.
-
[17]黄羹墙, 杨俊杰. 基于BP神经网络与马尔可夫链的短期电价预测[J]. 上海电力学院学报, 2017, 33(1): 1-3.
-
[18]李亚, 刘丽平, 李柏青, 等. 基于改进K-Means聚类和BP神经网络的台区线损率计算方法[J]. 中国电机工程学报, 2016, 36(17): 4543-4552.