发布时间: 2020-10-25
摘要点击次数:
全文下载次数:
DOI: 10.3969/j.issn.2096-8299.2020.05.017
2020 | Volume 36 | Number 5

计算机技术

一种基于深度学习的双JPEG图像压缩检测算法

楚雪玲, 魏为民, 华秀茹, 李思纤, 栗风永

上海电力大学计算机科学与技术学院, 上海 200090

收稿日期: 2020-04-08

基金项目: 国家自然科学基金（61602295）；上海市自然科学基金（16ZR1413100）

中图法分类号: TP391

文献标识码: A

文章编号: 2096-8299(2020)05-0505-06

摘要

双JPEG图像压缩检测是图像盲取证中的研究热点之一。针对JPEG图像压缩检测盲取证问题，提出了一种在双JPEG格式下基于卷积神经网络（CNN）的压缩检测算法。将图像数据集中的样本以不同的质量因子进行单JPEG压缩和双JPEG压缩，把检测图像的DCT系数直方图作为CNN网络的输入进行特征提取，输出层是样本类别的概率分类。实验结果表明，样本尺寸越大，篡改后的质量因子越大，分类器检测正确率越高；与现有算法相比，提出的算法检测正确率最高提高了1.3%，证明具有良好的双JPEG图像压缩性能检测能力。

关键词

双JPEG压缩; 图像盲取证; 深度学习; 卷积神经网络

A Double Compression Detection Algorithm for JPEG Image Based on Deep Learning

CHU Xueling, WEI Weimin, HUA Xiuru, LI Siqian, Li Fengyong

School of Computer Science and Technology, Shanghai University of Electric Power, Shanghai 200090, China

Abstract

Double JPEG compression detection is one of the research hotspots in blind forensics.To solve the problem of blind forensics a compression detection algorithm based on convolutional neural network (CNN) in double JPEG format is proposed.The samples in the image data set are compressed by single JPEG and double JPEG with different quality factors, and the DCT coefficient histogram of the detected image is taken as the input of CNN network for feature extraction.The output layer is the probability classification of the sample category.The experimental results show that the larger the sample size is, the larger the quality factor is, and the higher the detection accuracy is.Compared with present algorithms, this algorithm is of the highest accuracy, a rise of 1.3%, and has good detection ability of double JPEG compression performance.

Key words

double JPEG compression; blind image forensics; deep learing; convolutional neural network

盲取证技术在不知道原始来源的情况下, 利用统计和几何特征、插值效应或特征不一致可验证图像/视频的真实性。由于JPEG压缩可能会覆盖数字篡改的某些痕迹, 因此许多盲取证技术仅对未压缩的图像有效。然而, 大多数媒体捕获设备和后期处理软件(如PHOTOSHOP), 以JPEG格式输出图像, 而且互联网上的图像大多是JPEG格式的。因此, 对JPEG压缩鲁棒性研究的盲取证技术至关重要。原始JPEG图像(质量因子为Q_F1)被篡改后通常需要重新压缩, 即将经过数字篡改后的伪造图像以不同质量因子(Q_F2)的JPEG格式重新存储, 可能会引入双重JPEG压缩的证据。近年来, 许多成功的双JPEG图像压缩检测算法被提出。文献[1-2]分析了篡改前后的双量化(Double Quantilization, DQ)效应, 发现经过两次量化的图像区域的离散余弦变换(Discrete Cosine Transfrom, DCT)系数直方图一般呈现周期性, 不同于单量化区域的DCT系数直方图。文献[3]识别了DCT系数在时域与频域的周期性压缩伪迹, 可以检测块对齐和非对齐的双JPEG压缩。文献[4-5]提出单压缩图像的DCT系数一般遵循Benford定律, 而双压缩图像的DCT系数则违反了Benford定律。在文献[5]中, 采用DCT首位统计特征和支持向量机(Support Vector Machine, SVM)分类器相结合来对双JPEG压缩检测。文献[6]将双JPEG压缩应用于隐写术, 使用的特征是从低频DCT系数的统计中得到的, 不仅对普通的伪造图像有效, 而且对使用隐写算法处理的图像也有效。

然而, 上面讨论的算法有一个共同点, 它们只估计图像的压缩历史, 而不能准确地指出操作了哪个区域。文献[7]提出的算法是第一个通过分析DCT系数直方图中隐藏的DQ效应来自动定位局部篡改区域的算法。该算法使用贝叶斯方法估计了单个8×8块被篡改的概率, 得到的块后验概率图将显示篡改(单压缩)区域和未修改(双压缩)区域的视觉差异。为了更准确地定位篡改区域, 文献[8]利用先验知识, 即篡改区域应该是光滑的、聚类的, 并使用图像分割算法最小化一个已定义的能量函数来定位篡改区域。文献[9]探索了一种新的基于特征的技术, 使用残差的条件联合分布进行定位, 不仅计算效率高, 而且不受场景内容的影响。文献[10]基于文献[7]提出了更合理的概率模型, 计算了每个8×8块被双重压缩的可能性, 并结合一种估计初级量化质量因子的有效方法, 比文献[7]具有更好的性能。基于改进的统计模型, 文献[11]提出的方法既可以检测块对齐的压缩篡改区域, 也可以检测块非对齐的压缩篡改区域。文献[12]基于DCT系数的第一个数字特征对图像拼接结果进行定位, 并使用SVM进行分类。然而, 当Q_F1>Q_F2时, 这些方法的性能很差。

众所周知, 深度学习方法可以自动学习特征并进行分类。利用卷积神经网络(Convolutional Neural Network, CNN)的深度学习在语音识别、图像分类或识别、文档分析、场景分类等领域取得了很大的成功。对于隐写分析, 文献[13-14]利用CNN自动学习特征, 捕捉对隐写分析有用的复杂依赖关系, 结果令人大受鼓舞。事实上, 使用CNN的分层特征学习可以学习特定的特征表示, 具有深度模型的神经网络也可以有效地进行盲图像取证。

本文提出了一种利用CNN进行训练/测试的方法, 来检测双JPEG压缩篡改的图像。为了增强CNN的效果, 对DCT系数进行预处理。提取DCT系数的直方图作为输入, 然后设计一维CNN从这些直方图中自动学习特征并进行概率结果分类, 并与其他文献中的算法进行性能比较。

1 JPEG压缩背景介绍

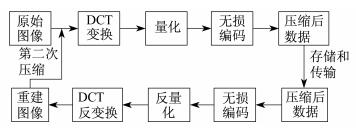
利用图像软件篡改图像时, JPEG图像在篡改完成之后, 可能会使用与原始图像质量因子Q_F1不同的质量因子Q_F2再一次压缩存储, 即JPEG图像的双重压缩。应当注意, 当Q_F1=Q_F2时, 图像特性改变不明显。图像双压缩过程如图 1所示。首先把原始JPEG图像解压缩, 即先解码和反量化; 再进行逆DCT变换; 最后对解压缩的图像执行第二次压缩。

图 1 双JPEG压缩过程

JPEG压缩是一种基于8×8块的方案, 将DCT系数应用于输入图像的8×8块, 然后量化DCT系数, 并对其应用舍入函数。量化系数进一步通过熵编码进行编码, 量化表对应每个特定的压缩质量因子Q_F, Q_F值为0~100的整数。Q_F值较低, 表示丢失了更多的信息。DCT系数的量化是造成压缩图像信息丢失的主要原因。

2 算法模型设计

2.1 特征设计

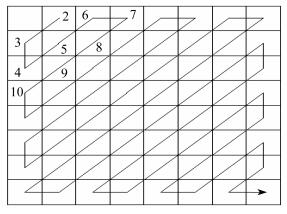
对给定的JPEG图像进行预处理。首先, 从JPEG头部提取其量化的DCT系数和最后一个质量因子, 在实验中, 只使用彩色图像的Y分量; 然后, 为每个DCT频率构造一个直方图。图像直流系数直方图的分布与交流系数的直方图不同, 可能会给特征设计带来困难, 因此本文算法只考虑交流系数。此外, 如果将整个直方图直接输入到CNN分类器中, 则训练操作会很复杂, 原因如下:首先, CNN的输入特征维数必须一致, 而直方图的大小总是变化的; 其次, 可能产生过高的培训计算成本。为了在不丢失重要信息的情况下降低特征向量的维数, 选择每个直方图峰值附近的指定区间(可能包含大部分重要信息)表示整个直方图。使用以下方法提取低频下的特征集, 具体如图 2所示。首先, 选取Zig-zag排列的第2~10个DCT系数构建特征集, 仅取对应于{-5, -4, …, 4, 5}被认为是有用的特性。设B为一个大小W×W的块, h_i(u)为DCT系数在第i个频率处的直方图, u在B中呈z字形排列。特征向量集由式(1)组成, 通过上述方法获得每个样本9×11维的特征向量。

图 2 Zig-zag取值示意

$ \begin{array}{l} {X_{\rm B}} = [{h_i}\left( { - 5} \right), {h_i}\left( { - 4} \right), {h_i}\left( { - 3} \right), {h_i}\left( { - 2} \right), \\ \;\;\;\;\;\;\;\;\;\;{h_i}\left( { - 1} \right), {h_i}\left( 0 \right), {h_i}\left( 1 \right), {h_i}\left( 2 \right), \\ \;\;\;\;\;\;\;\;\;\;{h_i}\left( 3 \right), {h_i}\left( 4 \right), {h_i}\left( 5 \right)]\\ i \in 2, 3, 4, \ldots , 10 \end{array} $

(1)

2.2 网络设计

CNN依赖于3个概念:局部接受域、共享权重和空间子采样^[15]。在每个卷积层中, 输出特征图通常表示与多个输入的卷积, 可以捕获相邻元素之间的局部依赖性。每个卷积连接之后都有一个池化层, 池化层以局部最大化或平均的形式执行子采样, 这样的子采样可以降低特征图的维数, 进而降低输出的灵敏度^[16]。在这些交替的卷积层和池化层之后, 输出特征图经过几个全连接, 然后输入到最终的分类层。分类层使用一个softmax连接来计算所有类的分布。

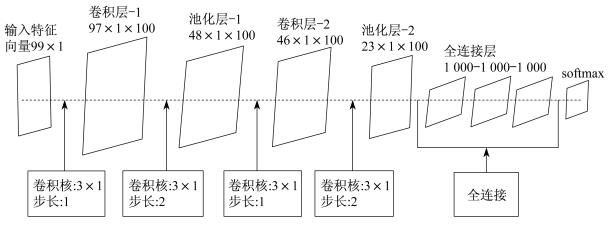
本文的CNN网络结构由2个卷积层、2个池化层连接和3个全连接层组成, 如图 3所示。

图 3 CNN网络结构

输入数据为9×11维的向量, 输出为两个类(单压缩/双压缩)概率的分布。对于卷积连接, 将卷积核m×n设为3×1, 卷积核数量k设为100, 滑动步长设为1。以第1卷积层为例, 输入数据的特征向量为99×1, 第1卷积层将这些特征数据与100个3×1的卷积核进行卷积, 步长为1。输出特征为97×1×100, 即特征图数量为100, 输出特征图维数为97×1。对于池化层, 同样将卷积核m×n设置为3×1, 池化步长设置为2, 观察到这种重叠池化可以防止训练过程中的过拟合。每个全连接层有1 000个神经元, 最后一个的输出与softmax层连接, 可以产生出每个样本应该被分类到每个类的概率。在JPEG图像伪造检测中, 只有单压缩和双压缩两类。

网络中每个连接层之间使用ReLU激活函数, 激活函数为f(x)=max(0, x)。在文献[17]中, 使用ReLU激活函数的深度学习网络收敛速度是传统学习网络的几倍, 对大型数据库的训练性能效果更佳。在全连接层中, 引入了“dropout”技术^[18]。其核心思想是在训练过程中从神经网络中随机抽取单元, 为有效地组合不同的网络结构提供一种方法。使用dropout技术, 可以有效地缓解过拟合, 缩短训练时间。

3 实验过程与结果分析

3.1 实验数据集

从Dresden Image Database图像数据库^[19]中选取tiff格式的500张原始图像, 70%进行训练, 30%做测试, 采用Q_F1为{60, 70, 80, 90, 95}进行第1次JPEG压缩, 采用Q_F2为{60, 65, 70, 75, 80, 85, 90, 95}进行第2次JPEG压缩, 将产生5组共1 750张单压缩图片和40组共14 000张双压缩图片, 图像块大小分别选择为64×64, 128×128, 256×256, 512×512, 1024×1024。实验环境为Python3.6, TensorFlow1.8.0.

3.2 实验结果与分析

设置不同的图像块大小, 检测其在CNN网络中不同Q_F2时所检测分类的正确率, 结果如表 1所示。

表 1 采用本文算法时Q_F2在图像不同尺寸下检测的正确率

下载CSV

尺寸	Q_F2
尺寸	60	65	70	75	80	85	90	95
64×64	0.726	0.683	0.727	0.763	0.801	0.824	0.848	0.975
128×128	0.775	0.776	0.788	0.842	0.814	0.925	0.947	0.986
256×256	0.801	0.826	0.830	0.855	0.831	0.950	0.984	0.993
512×512	0.912	0.931	0.869	0.913	0.909	0.992	0.995	0.998
1 024×1 024	0.931	0.992	0.993	0.993	0.992	0.993	0.995	1.000

文献[20]使用DCT首位统计特征和SVM分类器相结合进行双JPEG压缩检测。本文中同样的样本在文献[20]算法中检测的正确率如表 2所示。

表 2 采用文献[20]算法时Q_F2在图像不同尺寸下检测的正确率

下载CSV

尺寸	Q_F2
尺寸	60	65	70	75	80	85	90	95
64×64	0.737	0.708	0.732	0.707	0.713	0.811	0.878	0.971
128×128	0.775	0.776	0.779	0.818	0.804	0.923	0.941	0.984
256×256	0.801	0.827	0.832	0.853	0.831	0.948	0.984	0.991
512×512	0.862	0.889	0.851	0.907	0.868	0.976	0.992	0.996
1 024×1 024	0.919	0.976	0.985	0.985	0.971	0.982	0.992	0.999

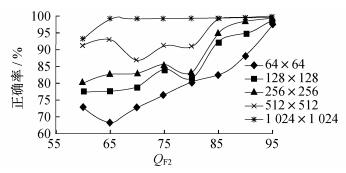
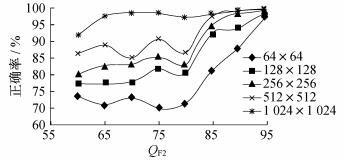
为了直观地观察出表 1和表 2数值变化的趋势, 将表 1和表 2数据分别生成图 4和图 5。

图 4 采用本文算法时Q_F2在图像不同尺寸下检测的正确率

图 5 采用文献[20]算法时Q_F2在图像不同尺寸下检测的正确率

由图 4和图 5可得出共同的结论:样本尺寸越大, 分类检测的正确率越高; 当样本尺寸大小为1 024×1 024时, 正确率都非常高; 本文提出的CNN算法性能明显优于文献[20]中的算法性能。首先, 对于卷积神经网络, 样本尺寸越大, 所包含的统计信息越多, 特征提取的也就越多, 分类器越容易进行区分, 所以检测正确率越高。其次, Q_F2值越大, 分类器分类的正确率越高, 当Q_F2为95时, 检测正确率在最大尺寸下达到100%。当Q_F1 < Q_F2时, 直方图会呈现周期性的值缺失, 且当Q_F2远大于Q_F1时, 直方图一个周期内的缺失值增多, 检测效果也会更好。

4 结语

分析JPEG图像双压缩的特征可知, 对于双JPEG压缩篡改检测而言, 第二次压缩的直方图与第一次压缩的直方图不同, 会出现很明显的周期值缺失或周期性极大值和极小值, 因此本文提出了一种CNN对JPEG图像双压缩的检测算法。将图像的DCT系数直方图作为CNN网络的输入进行特征提取, 利用深度学习可以用深层次网络自动学习到原始数据中隐含的关系, 而不需要对数据进行“显式”的预处理。实验结果表明, 与现有算法对比, 本文提出的算法检测率最高提高了1.3%, 证明了该方法在JPEG双压缩检测性能上的优越性。

参考文献

[1]

LUKÁŠ J, FRIDRICH J.Estimation of primary quantization matrix in double compressed JPEG images[C]//Proceedings of the 2003 Digital Forensic Research Workshop.Piscataway, NJ, USA: IEEE, 2003: 67-84.

[2]

FARID H. Exposing digital forgeries from JPEG ghosts[J]. IEEE Transactions on Information Forensics and Security, 2009, 4(1): 154-160. DOI:10.1109/TIFS.2008.2012215

[3]

CHEN Y L, HSU C T. Detecting recompression of JPEG images via periodicity analysis of compression artifacts for tamperingdetection[J]. IEEE Transactions on Information Forensics and Security, 2011, 6(2): 396-406. DOI:10.1109/TIFS.2011.2106121

[4]

FU D D, SHI Y Q, SU W.A generalized Benford's law for JPEG coefficients and its applications in image forensics[C]//Proceeding of SPIE-The International Society for Optics and Photonics, 2017, 6505: 65051L-11.

[5]

LI B, SHI Y Q, HUANG J W.Detecting doubly compressed JPEG images by using mode based first digit features[C]//IEEE 10th Workshop on Multimedia Signal.Processing.Cairns.Olds, Australia: IEEE, 2008: 730-735.

[6]

PEVNÝ T, FRIDRICH J. Detection of double-compression in JPEG images for applications in steganography[J]. IEEE Transactions on Information Forensics and Security, 2008, 3(2): 247-258. DOI:10.1109/TIFS.2008.922456

[7]

LIN Z, HE J, TANG X, et al. Fast, automatic and fine-grained tampered JPEG image detection via DCT coefficientanalysis[J]. Pattern Recognition, 2009, 42(11): 2492-2501. DOI:10.1016/j.patcog.2009.03.019

[8]

WANG W, DONG J, TAN T. Exploring DCT coefficient quantization effects for local tampering detection[J]. IEEE Transactions on Information Forensics and Security, 2014, 9(10): 1653-1666. DOI:10.1109/TIFS.2014.2345479

[9]

VERDOLIVA L, COZZOLINO D, POGGI G.A feature-based approach for image tampering detection and localization[C]//IEEE International Workshop on Information Forensics and Security (WIFS).Atlanta, GA, USA: IEEE, 2014: 149-154.

[10]

BIANCHI T, DE ROSA A, PIVA A.Improved DCT coefficient analysis for forgery localization in JPEG images[C]//IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP).Prague, Czech Republic: IEEE, 2011: 2444-2447.

[11]

BIANCHI T, PIVA A. Image forgery localization via block-grained analysis of JPEG artifacts[J]. IEEE Transactions on Information Forensics and Security, 2012, 7(3): 1003-1017. DOI:10.1109/TIFS.2012.2187516

[12]

AMERINI I, BECARELLI R, CALDELLI R, et al.Splicing forgeries localization through the use of first digit features[C]//IEEE International Workshop on Information Forensics and Security (WIFS).Atalnta, GA, USA: IEEE, 2014: 143-148.

[13]

QIAN Y, DONG J, WANG W, et al.Deep learning for steganalysis via convolutional neural networks[C]//Proceeding of SPIE-The International Society for Optics and Photonics, 2015, 9409: 94090J-10.

[14]

IAKOVIDOU C, ZAMPOGLOU M, PAPADOPOULOS S, et al. Content-aware detection of JPEG grid inconsistencies for intuitive image forensics[J]. Journal of Visual Communication and Image Representation, 2018, 54(5): 155-170.

[15]

楚雪玲, 魏为民, 华秀茹, 等. 面向JPEG图像篡改的盲取证技术综述[J]. 上海电力学院学报, 2019, 35(6): 607-613.

[16]

WANG Q, ZHANG R. Double JPEG compression forensics based on a convolutional neuralnetwork[J]. Eurasip Journal on Information Security, 2016(1): 23.

[17]

BELHASSEN B, MATTHEW C S.On the ronustness of constrained convolutional neural networks to JPEG post-conpression for image resampling detection[C]//IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP).New Orleans, LA, USA: IEEE, 2017: 2152-2156.

[18]

AMERINI I, URICCHIO T, BALLAN L, et al.Localization of JPEG double compression through multi-domain convolutional neural networks[C]//IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW).Honolulu, HI, USA: IEEE, 2017: 53-59.

[19]

Technische Universitat Dresden, Dresden, Germany.Dresden image database[EB/OL].(2015-05-01)[2020-04-08].http://forensics.inf.tu-dresden.de/ddimgdb.

[20]

YANG P P, NI R R, ZHAO Y.Double JPEG compression detection by exploring the correlations in DCT domain[C]//Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC).Honolulu, Hawaii, USA: IEEE, 2018: 728-732.