|
|
|
发布时间: 2020-12-25 |
|
|
|
|
收稿日期: 2019-12-17
中图法分类号: TM773
文献标识码: A
文章编号: 2096-8299(2020)06-0524-05
|
摘要
针对小电流接地系统两点接地故障的复杂性以及理论分析的难度,建立了仿真模型,分析了全部4种类型的两点接地故障,得到了故障时相电压、零序电压和零序电流的特征,提出了一种判断两点接地故障的方法。最后,通过PSCAD/EMTDC软件进行了仿真验证。
关键词
两点接地; 接地故障; 小电流接地系统; 配电网
Abstract
Aiming at the complexity and theoretical analysis difficulty of the cross-country grounded fault in the low current grounded system, a simulation model is established.Four types of the cross-country grounded fault are analyzed.Then, the characteristics of phase voltage, zero sequence voltage and zero sequence current are obtained.A method for detecting the cross-country grounded fault is proposed.Finally, the theoretical analysis is verified by PSCAD/EMTDC simulation.
Key words
cross-country grounded fault; grounded fault; the low current grounded system; the distribution network
我国中压配电网普遍采用小电流接地方式, 即中性点不接地和中性点经消弧线圈接地[1-2]。这种接地方式的优点是在配电网发生单相接地故障时, 线电压保持不变, 依规程可继续运行1~2 h, 供电可靠性较高。在此期间, 电网健全相承受较高电压(最大为1.732倍的正常电压), 线路绝缘薄弱处可能发生绝缘击穿, 从而发生第二次单相接地故障, 形成两点接地故障。根据故障点位置、相别的不同, 两点接地故障可以分为同一线路同一相别(同线同相)、同一线路不同相别(同线异相)、不同线路同一相别(异线同相)、不同线路不同相别(异线异相)等4种类型。与其他3种类型相比, 异线同相最为复杂。
目前, 故障选线装置对单相接地故障选线的准确率较高[3-4], 但大多数故障选线装置并不具备两点接地故障的判断能力。其主要原因是两点接地故障属于复杂故障, 受到中性点接地方式、故障点电阻、故障点距离、不平衡电压等复杂因素的影响, 理论分析计算难度较大[5-9]。文献[6]利用线性电路的基本定理和相序参数变换技术, 提出了一种/>小电流接地系统两点异相接地故障计算的方法。文献[7-8]分别分析了单电源和环网输电线路两点异地发生的接地故障。文献[9]采用小波分析工具研究了两点接地故障的保护原理。这些分析比较复杂, 一方面在课堂教学时学生难以理解, 另一方面在实际中应用难度也较大。因此, 本文通过PSCAD/EMTDC软件建立仿真模型进行仿真分析, 得到两点接地故障时电压和电流特点, 最后提出一种判断两点接地故障的方法。
1 理论分析
由于两相短路电流远大于负荷电流, 因此为简化计算, 突出两点接地故障的特点, 下面的分析中均不考虑负荷电流的影响。另外, 假设系统各元件正负序阻抗相等。
1.1 同线同相(第1类)
1.2 同线异相(第2类)
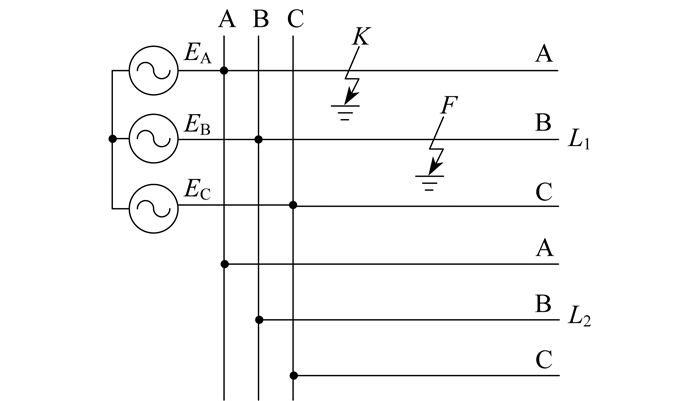
同线异相故障如图 2所示。
图 2中, 线路L1的A相在K点发生接地故障。一段时间后, 绝缘薄弱线路L1的B相在F点也发生接地故障。由于故障点K和F处于同一条线路但不同相别, 因此这种情况称为同线异相两点接地故障。为简化计算, 忽略故障电阻, A相和B相电流直接流入大地。根据电路分析理论[10], 有下列关系式
| $ {\mathit{\boldsymbol{I}}_{\rm{A}}}{\rm{ + }}{\mathit{\boldsymbol{I}}_{\rm{B}}}{\rm{ = }}0 $ | (1) |
| $ {\mathit{\boldsymbol{E}}_{\rm{A}}} + {\mathit{\boldsymbol{U}}_{\rm{N}}} = {\mathit{\boldsymbol{I}}_{\rm{A}}}{\mathit{\boldsymbol{Z}}_1}{d_K} $ | (2) |
| $ \begin{array}{l} {\mathit{\boldsymbol{E}}_{\rm{B}}} + {\mathit{\boldsymbol{U}}_{\rm{N}}} = \frac{1}{3}{\mathit{\boldsymbol{I}}_{\rm{B}}}(2{Z_1} + {Z_0})({d_F} - {d_K}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{I}}_{\rm{B}}}{Z_1}{d_K} \end{array} $ | (3) |
式中:IA, IB——A相和B相电流;
EA, EB——A相和B相电压;
UN——中性点电压;
Z1, Z0——线路单位长度的正序和零序阻抗;
dK, dF——故障点K和F至母线的距离。
联立式(1)~式(3), 可得
| $ {\mathit{\boldsymbol{I}}_{\rm{A}}} = - {\mathit{\boldsymbol{I}}_{\rm{B}}} = \frac{{{\mathit{\boldsymbol{E}}_{\rm{A}}} - {\mathit{\boldsymbol{E}}_{\rm{B}}}}}{{2{Z_1}{d_K} + \frac{1}{3}(2{Z_1} + {Z_0})({d_F} - {d_K})}} $ | (4) |
这种故障与两相短路接地故障不同, 文献[10]是指同一点两相同时发生接地故障, 故障相电压为零, 非故障相电压升高至额定电压的1.5倍。在本文所研究的同线异相两点接地故障中, 两个故障点之间存在距离, 母线上故障相电压降低, 零序电压增大, 仅在故障点之间存在零序电流。
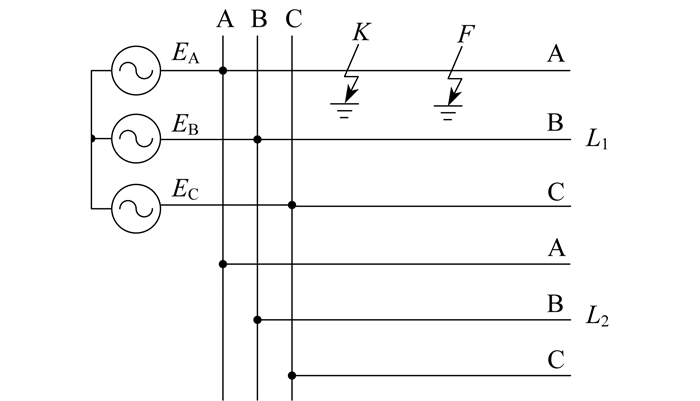
1.3 异线同相(第3类)
1.4 异线异相(第4类)
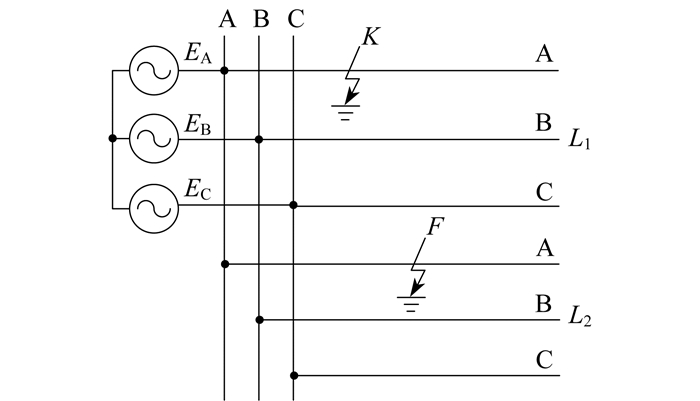
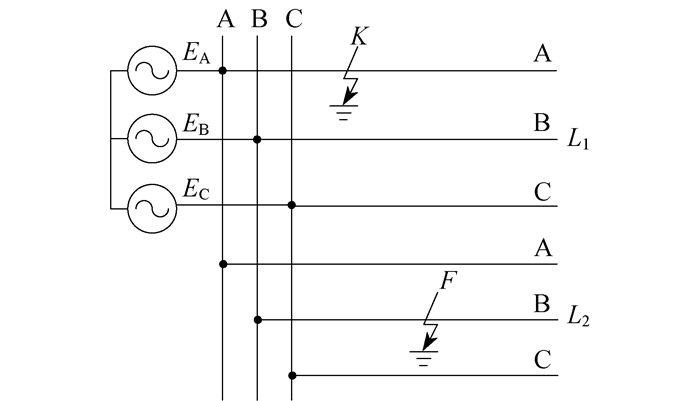
异线异相故障如图 4所示。
图 4中, 线路L1的A相在K点发生单相接地故障, 若干时间之后, 线路L2的B相在F点也发生了接地故障。这种情况称为异线异相两点接地故障。线路L1和L2相当于单相接地, 对于电源侧而言相当于两相短路。母线上故障相电压降低, 零序电压增大, 仅故障点K和F之间存在零序电流。可以得到
| $ {\mathit{\boldsymbol{I}}_{\rm{A}}} = - {\mathit{\boldsymbol{I}}_{\rm{B}}} = \frac{{{\mathit{\boldsymbol{E}}_{\rm{A}}} - {\mathit{\boldsymbol{E}}_{\rm{B}}}}}{{\frac{1}{3}(2{Z_1} + {Z_0})({d_K} + {d_F})}} $ | (5) |
2 仿真分析
2.1 同线同相接地故障仿真分析
仿真时故障设置为同线同相接地故障。这种类型的两点接地故障属于单相接地故障, 电压和电流的特征分析较多, 本文不再赘述。
2.2 同线异相接地故障仿真分析
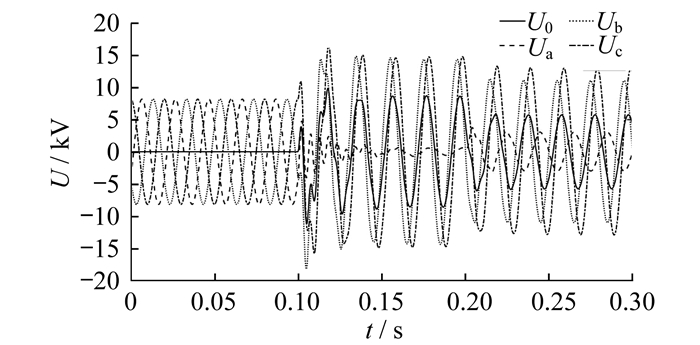
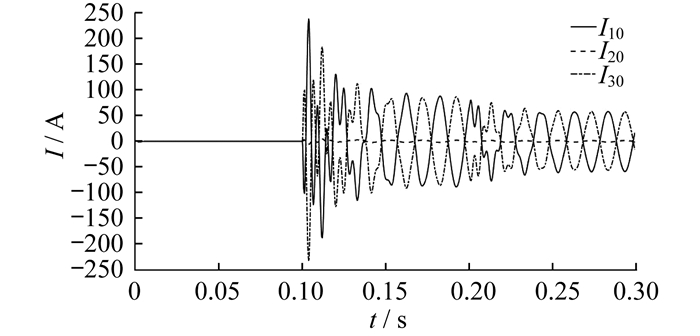
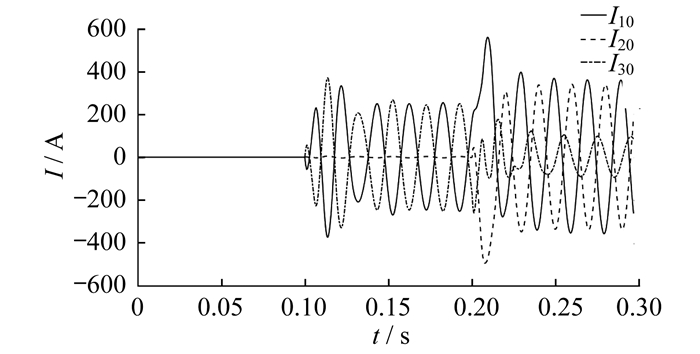
仿真时故障设置为同线异相接地故障, 即线路L1的A相在0.1~0.3 s时间段距母线10 km处发生接地故障, 当t=0.2 s时线路L1的B相在距母线25 km处发生接地故障。三相电压(Ua, Ub, Uc)、零序电压(U0)和3条线路上的零序电流(I10, I20, I30)分别如图 6和图 7所示。为突出故障期间电压或电流的变化规律, 本文没有截取故障恢复阶段的波形。
由图 6和图 7可以看出:在第1次故障发生后, 三相电压和零序电压均符合教材中单相接地故障的特征, 即故障相电压降低, 非故障相电压和零序电压升高, 线路中出现零序电流; 当第2次故障发生后, A相电压升高, B相和C相电压降低, 零序电压降低, 故障和非故障线路的零序电流都降低。
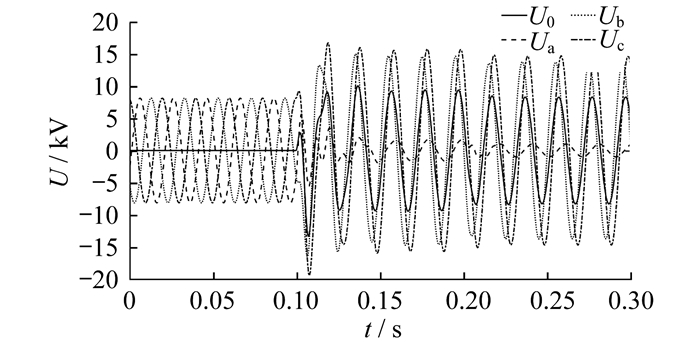
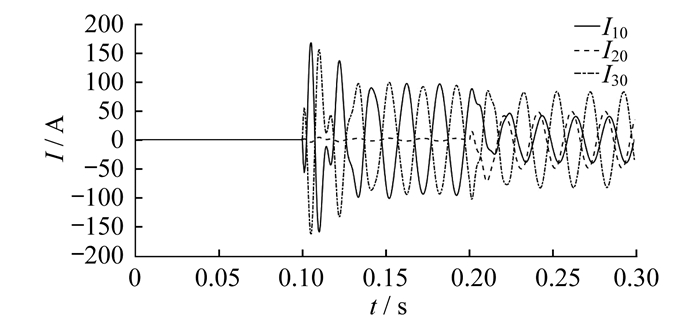
2.3 同线异相接地故障仿真分析
2.4 异线异相接地故障仿真分析
3 两点接地故障选线方法
通过上述理论与仿真分析, 可以归纳出两点接地故障时电压和电流的特征如表 1所示。
表 1
两点接地故障电压与电流的变化
| 故障类型 | 电压变化 | 电流变化 | |||
| 第1点接地 (与正常比较) |
第2点接地 (与第1点接地比较) |
第1点接地 (与正常比较) |
第2点接地 (与第1点接地比较) |
||
| 同线同相 | 故障相降低; 非故障相升高; 零序电压升高 | 不变 | 增加 | 不变 | |
| 同线异相 | 同上 | 第1故障相升高, 第2故障相降低; 非故障相降低; 零序电压降低 | 增加 | 均稍降 | |
| 异线同相 | 同上 | 相电压均稍降; 零序电压稍降 | 增加 | 第1故障线路降低, 第2故障线路升高; 非故障线路降低 | |
| 异线异相 | 同上 | 第1故障相升高, 第2故障相降低; 非故障相降低; 零序电压降低 | 增加 | 第1故障线路和第2故障线路均升高; 非故障线路降低 | |
同线同相故障与单相接地故障相同, 故可以按照传统的方法确定故障线路。同线异相故障类似于两相短路故障, 故也可以按照两相短路故障的措施处理。因此, 本文提出一种针对异线同相和异线异相两点接地故障的判断方法, 具体如下。
(1) 第1次接地故障可以按照传统方法判断出故障线路和故障相。监测零序电压变化。当零序电压降低时, 可认为发生第2次故障。
(2) 发生第2次故障后如果满足以下条件, 则为异线同相故障且零序电流升高者为故障线路:一是相电压和零序电压均有所降低; 二是第1故障线路零序电流降低。
(3) 发生第2次故障后如果满足以下条件, 则为异线异相故障且零序电流升高者为故障线路:一是第1故障相电压升高, 零序电压降低; 二是第1故障线路零序电流升高。
4 结语
两点接地故障是一种复杂的接地故障, 理论计算比较困难。本文通过仿真分析得到所有4类两点接地故障的电压和电流特征, 提出了判断两点接地故障的方法。后续可以对中性点经消弧线圈接地系统进行同样的仿真分析, 丰富两点接地故障判断的应用场景。
参考文献
-
[1]薛宏波, 唐颖杰, 吴芳芳, 等. 适合于城市电网中性点接地方式的选择[J]. 上海电力学院学报, 2017, 33(3): 221-228.
-
[2]徐波, 彭耀辉, 蔡翔. 相控式消弧线圈退出后电压振荡现象分析[J]. 上海电力学院学报, 2019, 35(4): 345-348.
-
[3]李丽, 龙登明. 基于小波包的配电网故障选线距离判别方法[J]. 上海电力学院学报, 2014, 30(5): 423-427.
-
[4]郭雨豪, 薛永端, 徐攀, 等. 含同母线环路的配电网单相接地故障特征及选线[J]. 电力系统自动化, 2019, 43(1): 234-242.
-
[5]刘道远, 程启明, 孙伟莎, 等. 电网电压不平衡条件下MMC控制策略的仿真比较研究[J]. 上海电力学院学报, 2019, 35(6): 553-561.
-
[6]曹国臣, 高宏慧. 小电流接地系统两点异相接地故障计算的新方法[J]. 电网技术, 2005, 29(5): 72-75.
-
[7]许建安. 中性点不接地系统两点异地接地及故障点位置判别[J]. 水电能源科学, 2008, 26(5): 193-195.
-
[8]CODINO A, GATTA F M, GERI A, et al.Detection of cross-country faults in medium voltage distribution ring lines[C]//Proceedings of the 2017 AEIT International Annual Conference.Cagliari, Italy, 2017: 20-22.
-
[9]MEDEIROS R P, COSTA F B. A wavelet-based transformer differential protection with differential current transformer saturation and cross-country fault detection[J]. IEEE Transactions on Power Delivery, 2018, 33(2): 789-799.
-
[10]李光琦. 电力系统暂态分析[M]. 北京: 中国电力出版社, 2007.
-
[11]李晓波, 蒋峰景, 李康, 等. 采用改进有源补偿技术的中性点电压柔性控制方法[J]. 电力系统自动化, 2016, 40(24): 111-117.
-
[12]薛永端, 李娟, 徐丙垠. 中性点经消弧线圈接地系统小电流接地故障暂态等值电路及暂态分析[J]. 中国电机工程学报, 2015, 35(22): 5703-5714.