|
|
|
发布时间: 2020-06-25 |
|
|
|
摘要
相变微胶囊悬浮液是集储热与强化传热功能于一体的新型工质。分别选取浓度为0.5%,0.75%,1.0%,2.0%和3.0%的相变微胶囊悬浮液,在长为650 mm、内径为2.5 mm、外径为3 mm的不锈钢圆管中进行了换热实验。结果表明:在放热过程中,壁面无量纲温度随浓度的增加而逐渐增加,局部努塞尔数随浓度的增加而逐渐减小;随着沿程的不断增大,壁面无量纲温度出现先增大后减小的趋势,局部努塞尔数呈逐渐降低的趋势。
关键词
相变微胶囊悬浮液; 圆管; 换热
Abstract
Phase change microcapsule suspension is a new working medium which integrates heat storage and heat transfer enhancement.Phase change microcapsule suspensions with mass concentrations of 0.5%, 0.75%, 1%, 2% and 3% were selected to conduct heat transfer experiments in stainless steel circular tubes with a length of 650 mm, inner diameter of 2.5 mm and outer diameter of 3 mm.The results show that the dimensionless temperature of the wall surface increases with the increase of mass concentration, and the local Nusselt number decreases with the increase of concentration.Along the flow direction of the suspension, the dimensionless temperature of the wall surface increases first and then decreases, and the local Nusselt number decreases gradually.
Key words
phase change microcapsule suspension; circular tube; heat transfer
随着社会的不断进步与经济的快速发展, 全球能源短缺问题日益严重, 提高能源使用效率和开发新能源是人类面临的重要课题[1]。相变微胶囊悬浮液由于相变微胶囊颗粒发生相变时吸收或放出大量热量, 并与周围流体发生微对流效应, 增强了悬浮液与壁面的换热效果, 是集储热和强化传热于一体的一种新型材料, 因此在太阳能利用、电子设备冷却、采暖和空调领域具有广泛的应用前景[2]。
王利[3]通过实验发现, 影响相变微胶囊悬浮液强化传热的主要因素是雷诺数(Re)和微胶囊的体积分数, 而斯蒂芬数的影响很微小。鲁进利等人[4]经过研究发现, 影响相变微胶囊悬浮液强化传热的较大因素有雷诺数、微胶囊的颗粒浓度、壁面热流密度。田丽亭等人[5]通过实验发现, 相变微胶囊颗粒的加入明显增强了溶液的冷却效果, 有效降低了管道壁面温度, 并且悬浮液浓度越高, 管道壁面温度越低。钟小龙等人[6]在实验中发现, 管壁壁面温度受雷诺数和相变微胶囊悬浮液浓度的影响较大。仇中柱等人[7]研究发现, 质量分数和斯坦顿数(St)对强化传热的效果影响较大, 而相变微胶囊颗粒的粒径大小、过冷度强化传热的效果影响较小。INABA H等人[8]研究发现, 在相同雷诺数下, 相变微胶囊悬浮液的平均换热系数是水的2.0~2.8倍。
综上所述, 相变微胶囊悬浮液可以有效强化传热, 它的流动和传热特性取决于以下参数:相变微胶囊悬浮液流速、质量浓度、传热系数、努塞尔数(Nu)、雷诺数、斯坦顿数、均匀度、过冷度、相变温度范围和粒径分布等。这些参数的影响是已知的, 但在不同的实验中影响程度不同, 仍处于探索状态[9]。本文搭建了一个实验系统, 对不同浓度的相变微胶囊悬浮液流过细小圆管时与壁面的对流换热特性进行了实验研究。
1 实验装置和方法
1.1 实验装置
实验装置如图 1所示。相变微胶囊悬浮液由微型流量泵从磁力搅拌器上的恒温烧杯中吸出, 通过主循环回路流量调节阀和旁通回路流量调节阀的调节, 控制进入流量计的流量; 一部分悬浮液直接通过旁通回路流量调节阀返回恒温烧杯, 另一部分进入实验段进行换热, 换热后返回恒温烧杯后继续循环。磁力搅拌器恒温烧杯出口的温度为30 ℃。
实验采用长为650 mm、内径为2.5 mm、外径为3 mm的304不锈钢圆管, 其热导率为16.3 W/(m·K), 并且在不锈钢圆管均匀包裹上4个K型热电偶形成实验段。K型热电偶温度信号通过安捷伦数据采集仪(Agilent34970A)采集后, 由电脑输出。
实验采用大龙兴创实验仪器(北京)有限公司生产的LCD数控加热型23.33 cm方盘磁力搅拌器, 型号为MS7 - H550 - Pro; 乔穆自动化科技有限公司生产的K型贴片式热电偶, 型号为Tpsk; 南京润泽流体控制设备有限公司生产的倒锥接头, 型号为WD10A-1/4-28-P和YC-032-P; 南京润泽流体控制设备有限公司生产的特氟龙管, 型号为TFLG00006;卡默尔流体科技(上海)有限公司生产的微型流量泵, 型号为NKCP-S10B。
1.2 实验材料
1.2.1 相变微胶囊物理特性
相变微胶囊材料在相变的过程中能吸收或者释放出大量的潜热。本实验建立在放热的基础上, 由磁力搅拌器加热微胶囊悬浮液到30 ℃, 芯材发生融化吸热变为熔融态, 其微观颗粒的熔融状态如图 2所示。
实验所采用的相变微胶囊颗粒, 其芯材为石蜡, 壁材为密胺树脂, 相变微胶囊材料的平均相变温度为28 ℃, 微胶囊颗粒的相变焓值大约为120 J/g。室温下, 其外观为白色粉末状颗粒物, 约含有68%石蜡和32%的密胺树脂, 其平均颗粒直径为8 μm。将相变微胶囊与蒸馏水配成不同质量分数的相变微胶囊悬浮液, 经过研究发现, 相变微胶囊在蒸馏水中有很好的分散性。
1.2.2 相变微胶囊悬浮液密度
在实验中需要计算相变微胶囊悬浮液的整体密度。首先计算单个相变微胶囊颗粒的密度, 用ρp表示单个相变微胶囊颗粒密度, 用ρb表示相变微胶囊悬浮液的密度。
| $ {{\rho _{\rm{p}}} = {\rho _{\rm{c}}}{c_{\rm{m}}} + {\rho _{{\rm{wi}}}}(1 - {c_{\rm{m}}})} $ | (1) |
| $ {{\rho _{\rm{b}}} = {\rho _{\rm{p}}}{c_{\rm{v}}} + {\rho _{{\rm{wj}}}}(1 - {c_{\rm{v}}})} $ | (2) |
式中:ρc——芯体相变材料密度, kg/m3;
cm——相变微胶囊悬浮液的质量分数, %;
ρwi——壳体材料密度, kg/m3;
cv——相变微胶囊悬浮液中相变微胶囊颗粒的体积分数, %;
ρwj——蒸馏水的密度, kg/m3。
1.2.3 相变微胶囊悬浮液的导热系数
用kp表示单个相变微胶囊颗粒的导热系数, 用kb表示相变微胶囊悬浮液的平均导热系数。
| $ {\frac{1}{{{k_{\rm{p}}}{d_{\rm{p}}}}} = \frac{1}{{{k_{\rm{c}}}{d_{\rm{c}}}}} + \frac{{{d_{\rm{p}}} - {d_{\rm{c}}}}}{{{k_{{\rm{wi}}}}{d_{\rm{p}}}{d_{\rm{c}}}}}} $ | (3) |
| $ {\frac{{{k_{\rm{b}}}}}{{{k_{{\rm{wj}}}}}} = \frac{{2 + \frac{{{k_{\rm{p}}}}}{{{k_{{\rm{wj}}}}}} + 2{c_{\rm{v}}}\left( {\frac{{{k_{\rm{p}}}}}{{{k_{{\rm{wj}}}}}} - 1} \right)}}{{2 + \frac{{{k_{\rm{p}}}}}{{{k_{{\rm{wj}}}}}} - {c_{\rm{v}}}\left( {\frac{{{k_{\rm{p}}}}}{{{k_{{\rm{wj}}}}}} - 1} \right)}}} $ | (4) |
式中:dp, dc——颗粒和芯材的直径, μm;
kc——相变微胶囊中芯材的导热系数, W/(m·K);
kwi——壳材料的导热系数, W/(m·K);
kwj——蒸馏水的导热系数, W/(m·K)。
1.2.4 相变微胶囊悬浮液黏度
用ub表示相变微胶囊悬浮液的平均黏度。
| $ \frac{{{u_{\rm{b}}}}}{{{u_{\rm{w}}}}} = {(1 - {c_{\rm{v}}} - 1.16c_{\rm{v}}^2)^{ - 2.5}} $ | (5) |
式中:uw——蒸馏水的黏度, Pa·s。
式(5)黏度关系式适用于颗粒浓度在0%~20%、颗粒平均粒径在0.3~400 μm的情况。应用式(1)~式(5), 可以得出相变微胶囊颗粒及相变微胶囊悬浮液的物性参数[10-12]如表 1所示。
表 1
相变微胶囊悬浮液的物性参数
| 物质 | 密度/(kg·m-3) | 导热系数/[W·(m·K)-1] | 动力黏度/10-3(Pa·s) | 潜热/(J·g-1) | |
| 蒸馏水(30 ℃) | 995.70 | 0.618 | 0.802 | ||
| 石蜡 | 912.00 | 0.210 | 189 | ||
| 密胺树脂 | 1 500.00 | 0.200 | |||
| 相变微胶囊颗粒 | 1 100.00 | 0.162 | 100 | ||
| 相变微胶囊悬浮液 | cm=0.50% | 996.22 | 0.614 | 0.812 | |
| cm=0.75% | 996.48 | 0.613 | 0.817 | ||
| cm=1.00% | 996.74 | 0.612 | 0.822 | ||
| cm=2.00% | 997.79 | 0.606 | 0.845 | ||
| cm=3.00% | 1 008.70 | 0.599 | 0.868 | ||
2 数据处理与分析
2.1 数据处理
相变微胶囊的相变温度为28 ℃, 实验中利用磁力搅拌器将悬浮液加热至30 ℃, 因从磁力搅拌器恒温槽到实验段入口段较短, 此段的热损失和热阻可以忽略不记, 因此实验入口温度为30 ℃。
实验中圆管的进口雷诺数为
| $ Re = \frac{{{u_{\rm{m}}}{d_{\rm{i}}}}}{{{v_{\rm{b}}}}} = \frac{{\rho {u_{\rm{m}}}{d_{\rm{i}}}}}{\mu } = \frac{{4\rho f}}{{{\rm{ \mathsf{ π} }}{d_{\rm{i}}}\mu }} $ | (6) |
式中:um——相变微胶囊的进口速度, m/s;
di——圆管内径, m;
vb——悬浮液运动黏度, m2/s;
ρ——相变微胶囊的密度, g/cm3;
μ——悬浮液动力黏度, Pa·s;
f——流量计所测的流量, kg/s。
圆管无量纲壁面温度θw, x、圆管内壁面局部温度Twi, x、管内流体局部温度Tb, x分别为
| $ {{\theta _{{\rm{w,x}}}} = \frac{{2{\lambda _{\rm{b}}}({T_{{\rm{wi,x}}}} - {T_{{\rm{in}}}})}}{{{d_{\rm{i}}}{q_{\rm{w}}}}}} $ | (7) |
| $ {{T_{{\rm{wi,x}}}} = {T_{{\rm{wo,x}}}} - \frac{{Q\ln \left( {\frac{{{d_0}}}{{{d_{\rm{i}}}}}} \right)}}{{2{\rm{ \mathsf{ π} }}{\lambda _{\rm{w}}}L}}} $ | (8) |
| $ {{T_{{\rm{b,x}}}} = {T_{{\rm{in}}}} + \frac{{{q_{\rm{w}}}{\rm{ \mathsf{ π} }}{d_{\rm{i}}}x}}{{m{c_{{\rm{p,b}}}}}}} $ | (9) |
式中:λb——流体的导热系数, W/(m·K);
Tin——圆管内流体的进口温度, K;
qw——圆管壁面加热热流密度, W/m2;
Two, x——圆管外壁面局部温度, K;
Q——输入功率, W;
do——圆管外径, m;
λw——圆管的导热系数, W/(m·K);
L——圆管长度, m;
x——距离圆管入口处的长度, m;
m——圆管内流体的质量流量, kg/s;
cp, b——流体的比热容, J/(kg·K)。
实验圆管的局部换热系数hx和局部努塞尔数Nux分别为
| $ {{h_{\rm{x}}} = \frac{{{q_{\rm{w}}}}}{{\Delta {T_{\rm{x}}}}} = \frac{Q}{{{\rm{ \mathsf{ π} }}{d_0}L({T_{{\rm{wi,x}}}} - {T_{{\rm{b,x}}}})}}} $ | (10) |
| $ {N{u_{\rm{x}}} = \frac{{{h_{\rm{x}}}}}{{{\lambda _{\rm{b}}}}}} $ | (11) |
式中:ΔTx——壁面温度与流体温度的局部温差, K。
3 实验结果与讨论
3.1 不同浓度下相变微胶囊悬浮液换热特性探究
3.1.1 管道壁面温度
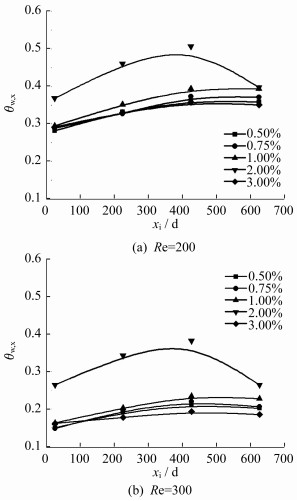
雷诺数为200和300, 浓度为0.50%, 0.75%, 1.00%, 2.00%, 3.00%的相变微胶囊悬浮液其管道无量纲壁面温度θw, x随流动方向的变化曲线, 如图 3所示。
由图 3可以看出, 在雷诺数不同的情况下, 无量纲壁面温度随着沿程的逐渐增加呈先增大后减小的趋势。在雷诺数不变的条件下, 在浓度为0.50%~3.00%的相变微胶囊悬浮液中, 悬浮液浓度越大, 管道无量纲壁面温度增加或减小的幅度越大, 其中2.00%的相变微胶囊悬浮液的无量纲壁面温度最高, 而3.00%的相变微胶囊悬浮液的无量纲壁面温度最低。究其原因在于:当浓度继续增加到3.00%时, 悬浮液中相变微胶囊颗粒浓度增大, 流经管道的时间较短, 使得悬浮液中部分相变微胶囊颗粒尚未完全放热而流出通道; 雷诺数增大后, 相变微胶囊悬浮液在管道内的流速加大, 流经管道的时间缩短, 使得悬浮液中大量的热量被带出通道。
3.1.2 管道局部努塞尔数
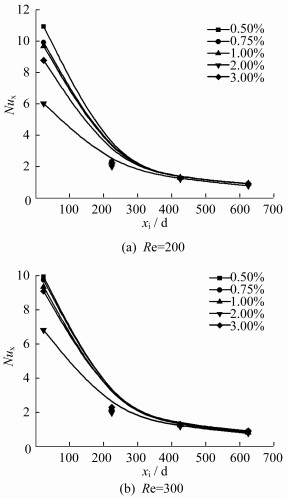
雷诺数为200和300, 浓度为0.50%, 0.75%, 1.00%, 2.00%, 3.00%的相变微胶囊悬浮液其管道局部努塞尔数Nux随流动方向的变化曲线, 如图 4所示。
由图 4可以看出, 当雷诺数增大时, 整体换热增强的幅度减弱。在管道的入口段, 浓度为0.50%的悬浮液明显优于更高浓度的悬浮液, 这是由于低浓度的悬浮液刚进入圆管时, 贴近壁面的微胶囊颗粒率先与管壁接触并开始放热, 同时悬浮液的高导热率和低黏度使热量能及时高效地与管壁进行对流换热。随着悬浮液向下游流动, 管道壁面换热增强的幅度减弱, 在管道中部时悬浮液换热几乎相近, 而在接近管道的出口处, 悬浮液的Nux略有差异。相变微胶囊悬浮使管道入口段的Nux减小幅度明显较大, 但随着沿程的变化, 对流换热幅度减弱。究其原因在于:悬浮液刚进入圆管时, 贴近壁面的微胶囊颗粒开始释放热量, 同时微胶囊颗粒和周围流体存在微对流效应, 增强了管道壁面的对流换热; 随着沿程的变化, 靠近壁面的热边界层不断加厚, 流动径向热阻加大, 悬浮液中的微胶囊颗粒不能尽快放热相变, 最终随悬浮液流出管道。
4 结论
本文搭建了细小圆管内相变微胶囊悬浮液换热的实验系统, 对浓度分别为0.50%, 0.75%, 1.00%, 2.00%, 3.00%的相变微胶囊悬浮液在细小圆管内放热过程的换热特性进行了实验研究, 得到如下结论。
(1) 在本文选定的实验工况下, 相变微胶囊悬浮液可以强化传热, 并且在放热过程中, 圆管壁面的无量纲温度随浓度的增加而逐渐增加。
(2) 在选定的雷诺数条件和不同浓度的相变微胶囊悬浮液中, 浓度为2.00%的悬浮液换热效果最好, 这是因为3.00%的悬浮液颗粒浓度较大, 悬浮液中大量微胶囊颗粒尚未完成放热相变就已经流出管道。
(3) 当雷诺数一定时, 不同浓度的相变微胶囊悬浮液的Nux均随沿程的增加而减小, 且随着悬浮液浓度的增加, Nux呈现减小趋势; 相变微胶囊悬浮使管道入口段的Nux减小幅度较大, 但随着沿程的增加对流换热幅度减弱。
参考文献
-
[1]孙建梅, 刘云昭. 可再生能源在建筑节能中的应用[J]. 绿色科技, 2014(1): 239-241.
-
[2]钟小龙, 刘东, 胥海伦. 相变微胶囊悬浮液在低温热水地板辐射供暖系统中的应用研究[J]. 绿色建筑, 2016, 8(2): 93-97.
-
[3]王利.微胶囊相变悬浮液管内层流强化传热性能的实验研究[D].天津: 天津大学, 2006.
-
[4]鲁进利, 韩亚芳, 钱付平, 等. 圆管中相变微胶囊悬浮液层流状态下的融化特性[J]. 过程工程学报, 2013, 13(1): 152-157.
-
[5]田丽亭, 李帅, 崔志强, 等. 圆管内相变微胶囊悬浮液换热特性实验研究[J]. 热能动力工程, 2018, 33(10): 16-21.
-
[6]钟小龙, 刘东, 胥海伦. 微小管道内相变微胶囊悬浮液换热特性[J]. 化工学报, 2016, 67(增刊1): 203-209.
-
[7]仇中柱, 罗鹏, 秦承芳, 等. 等热流圆管内相变微胶囊悬浮液层流换热实验研究[J]. 热科学与技术, 2017, 16(2): 137-143.
-
[8]INABA H, KIM M J, HORIBE A. Melting heat transfer characteristics of microencapsulated phase change material slurries with plural microcapsules having different diameters[J]. J Heat Transfer, 2004(4): 558-565.
-
[9]吕珊, 仇中柱, 秦承芳, 等. 影响微胶囊相变悬浮液稳定性因素的理论分析[J]. 上海电力学院学报, 2016, 32(3): 221-224.
-
[10]GOEL M, ROY S K, SENGUPTA S. Laminar forced convection heat transfer in microcapsulated phase change material suspensions[J]. Int J Heat Mass Transfer, 1994, 37(4): 593-604.
-
[11]ROY S K, AVANIC B L. Turbulent heat transfer with phase change material suspensions[J]. Int J Heat Mass Transfer, 2001, 44(12): 2277-2285.
-
[12]HU X X, ZHANG Y P. Novel insight and numerical analysis of convective heat transfer enhancement with microencapsulated phase change material slurries:laminar flow in a circular tube with constant heat flux[J]. Int J Heat Mass Transfer, 2002, 45(15): 3163-3172.