|
|
|
发布时间: 2021-02-25 |
清洁安全发电 |
|
|
|
收稿日期: 2019-12-20
基金项目: 国家科技重大专项(2017-V-0011-0063);上海市"科技创新行动计划"地方院校能力建设专项项目(19020500700)
中图法分类号: TM621.6
文献标识码: A
文章编号: 2096-8299(2021)01-0017-06
|
摘要
燃气轮机控制系统在电厂安全运行中起到重要作用,而传感器作为控制系统中的测量信号装置,其安全性至关重要,因此开展对燃气轮机控制系统传感器的故障诊断研究具有重要意义。在传感器故障诊断中,需要从故障信息中提取出有效的诊断规则。为了解决这一问题,提出了一种改进离散化方法对数据进行预处理,结合粗糙集(RS)和径向基(RBF)神经网络对传感器进行故障诊断研究。实验结果表明,该方法减少了燃气轮机控制系统传感器故障类型的误判率。
关键词
燃气轮机控制系统; 离散化; 粗糙集; RBF神经网络; 故障诊断
Abstract
The gas turbine control system plays an important role in the safe operation of the power plant, and the sensor, as the measuring signal device in the control system, is of vital importance in safety.Therefore, it is of great significance to carry out the fault diagnosis research on the sensor of the gas turbine control system.In sensor fault diagnosis, it is necessary to extract effective diagnosis rules from fault information.In order to solve this problem, an improved discretization method is proposed to preprocess data, and the sensor fault diagnosis is studied by combining RS(rough set)and RBF(radial basis function) neural network.The experimental results show that this method can reduce the misjudgment rate of sensor fault types in gas turbine control system.
Key words
gas turbine control system; discretization; rough set; radial basis function neural network; fault diagnosis
燃气轮机在国家发电体系中具有非常重要的作用, 其控制系统控制着燃气轮机的安全稳定运行[1]。传感器作为控制系统中重要的测量元件, 负责测量各种信号来监测燃气轮机的运行状态, 并及时反馈给控制系统。因此, 当发生故障时, 就需要对其进行故障诊断以判断其故障类型, 避免后续造成巨大损失[2]。
常见的燃气轮机控制系统传感器故障诊断方法主要分为基于解析模型的方法和基于数据驱动的方法[3]。其中基于解析模型的方法需要对燃气轮机的控制系统进行准确的数学建模, 但是由于燃气轮机控制系统是一种复杂的、非线性的动态系统, 因此难以对其进行准确的建模来反映实时的系统状态。为此, 本文采用基于数据驱动的方法对燃气轮机控制系统传感器的故障进行诊断。该方法不需要对燃气轮机控制系统建立准确的数学模型, 只需对其运行数据进行分析即可。
信息融合是一种常用的基于数据驱动的故障诊断方法, 具有多种分类[4], 其中贝叶斯理论和DS证据理论是基于知识的理论方法, 需要获得相关问题的先验知识, 而这些知识往往在实际问题中很难获得, 从而使得这些方法存在一定的局限性[5]。粗糙集(Rough Set, RS)理论的优势在于不依赖先验知识, 可以通过对故障数据的条件属性和决策属性进行分析和推理, 从中找出潜在的规律, 从而对条件属性进行约简, 去除其中一部分相关性较低的条件属性, 得到简化的传感器故障诊断决策表[6]。RS理论的缺点在于其容错能力较低, 也意味着单独的RS理论无法满足故障诊断的实际需求[7]; 而神经网络作为一种广泛应用于各个领域的技术, 与其他领域的技术具有很强的兼容性, 因此可以将神经网络与RS理论相结合, 从而形成复合的故障诊断系统[8]。
然而, 在实际的燃气轮机运行过程中, 不仅产生离散数据, 还存在着大量的连续数据。RS理论只适用于离散属性, 因此就需要选择一种合适的离散化方法。等频离散化方法是一种较为常用的离散化方法[9]。本文利用改进的等频离散化方法对燃气轮机控制系统传感器的故障征兆属性进行离散化处理, 而后利用RS理论消除与故障类型关联度低的条件属性; 最后, 利用径向基(Radial Basis Function, RBF)神经网络完成对燃气轮机控制系统传感器故障类型的诊断。实验结果表明, 改进离散化方法与粗糙集神经网络的良好结合, 在燃气轮机控制系统传感器故障诊断中可以取得更好的效果。
1 等频离散化方法及其改进
1.1 等频离散化方法
等频离散化方法将数据放在k个区间, 每个区间大约包含p/k个数据, 保证每个区间数据的数量大致相同, 其中p为数据的总个数。
等频离散化方法作为一种常用的连续属性离散化方法, 优点是减少了异常值的影响, 可以在同一个区间内收集相似的数据。缺点是很难找到最佳区间数k, 而且可能将大小相同的值放在不同的区间中。
以一组数据{10, 20, 30, 40, 20, 50, 20, 60, 20}为例, 对其进行等频离散化处理。设置区间数k为3, 每个区间内数据的数量为p/k=3。由于数据中存在重复数值, 且重复值的数量大于区间中的数据数量, 这时就会导致等频离散化方法将相同的数值分配到不同的区间中, 从而对后续的故障诊断造成不利影响。
1.2 改进的等频离散化方法
由于等频离散化方法会将两个相同的数据分到不同的区间中, 影响后续故障诊断时的精度, 而且找出最优区间数k是一个困难的问题, 因为k值过小会导致信息的丢失, k值过大不能很好地反映结果。因此, 在对数据进行离散化处理时, 可以先消除数据中的重复值, 得到q个非重复的数据, 这样就可以防止相同的数据被分到不同的区间, 避免对后续的故障诊断造成影响。设置离散区间数k的值为
(1) 分别输入待离散化的故障征兆集合A中的各个故障征兆属性Ai={a1, a2, a3, …, ap-1, ap}(i=1, 2, 3, …, n);
(2) 将Ai中的所有值按升序排列;
(3) 得到非重复值A′i={a1, a2, a3, …, aq-1, aq};
(4) 设置区间数k的值为
(5) 根据每个区间的元素数量创建k个数据集Bj(j=1, 2, 3, …k)来存放数据, 并计算每个数据集中数据的平均值Bavgj(j=1, 2, 3, …, k);
(6) 通过计算离散区间的边界
(7) 通过确定A′i中各值所属的区间, 将它们的连续值转化为离散值;
(8) 输出离散化后的条件属性集合C中各条件属性Ci(i=1, 2, 3, …, n)。
同样以一组数据{10, 20, 30, 40, 20, 50, 20, 60, 20}为例, 用改进后的等频离散化方法对其进行处理, 去除重复值并按升序排序, 得到非重复值{10, 20, 30, 40, 50, 60}。由此可以得到区间数k的值为2, 并得到两个数据集分别为B1={10, 20, 30}, B2={40, 50, 60}。计算两个数据集中数据的平均值分别为Bavg1=20, Bavg2=50, 由此得到区间的边界为35。最终得到两个离散区间分别为I1=[10, 35), I2=[35, 60]。可以看到, 改进后的等频离散化方法通过选取属性唯一值而得到离散区间, 避免了重复值被分到不同的区间中; 同时通过设置区间数k的值为
2 粗糙集神经网络
2.1 粗糙集理论
对于一个信息决策系统S=(U, R, V, f), 其中: U是对象集合; R是属性集合, 包含条件属性集合C和决策属性集合D; V是属性的值域; f是一种映射, 反映对象的属性值[11]。
设X为U的非空子集, B为R的非空子集, 定义X的下近似集为
| $ {B_ - }(X) = \cup \left\{ {x\mid \left( {x \in U \wedge {{[X]}_B} \subseteq X} \right)} \right\} $ | (1) |
定义X关于B的正域为
| $ {{\mathop{\rm POS}\nolimits} _B}(X) = {B_ - }(X) $ | (2) |
决策属性集合D对条件属性集合C的依赖程度可以表示为
| $ {\gamma _C}(D) = \frac{{\left| {{{{\mathop{\rm POS}\nolimits} }_C}(D)} \right|}}{{|U|}} $ | (3) |
条件属性Ci对于决策的重要程度可以定义为
| $ {\mathop{\rm SGF}\nolimits} \left( {{C_i}, C, D} \right) = {\gamma _c}(D) - {\gamma _{c - {c_i}}}(D) $ | (4) |
若SGF(Ci, C, D)=0, 则Ci对于决策属性来说是冗余的。
2.2 RBF神经网络
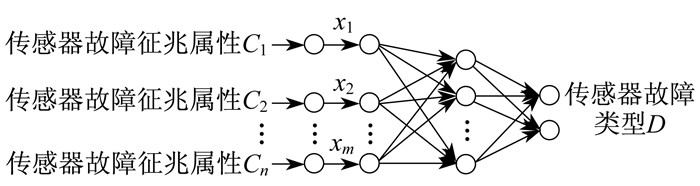
图 1为粗糙集RBF神经网络故障诊断模型, 包含粗糙集约简层、输入层、隐藏层和输出层4层[12]。
粗糙集约简层的每个输入对应的是传感器的每个故障征兆, 也就是传感器故障诊断决策表中的条件属性。有n个条件属性的传感器故障样本在经过粗糙集约简层之后会被约简为具有m个条件属性的传感器故障样本, 最后将其输入到RBF神经网络当中。
可以得知, RBF神经网络的输入节点数为约简后的条件属性数m, 输出节点数根据故障类型编码的维数来选择, 记为l, α为1~10之间的常数。隐藏层节点数s的计算公式为
| $ s = \sqrt {m + l} + \alpha $ | (5) |
选取高斯函数作为隐藏层神经元的作用函数, 对输入信息进行空间映射的变换, 输出层再对其进行线性加权输出故障诊断结果。RBF神经网络的输入输出响应为
| $ {y_j} = \sum\limits_{i = 1}^m {{\varpi _{ij}}} \exp \left( { - \frac{{\left\| {{x_i} - {c_i}} \right\|}}{{2\delta _i^2}}} \right) $ | (6) |
式中:
‖xi-ci‖——欧氏范数;
δi——高斯函数的方差。
3 实验分析
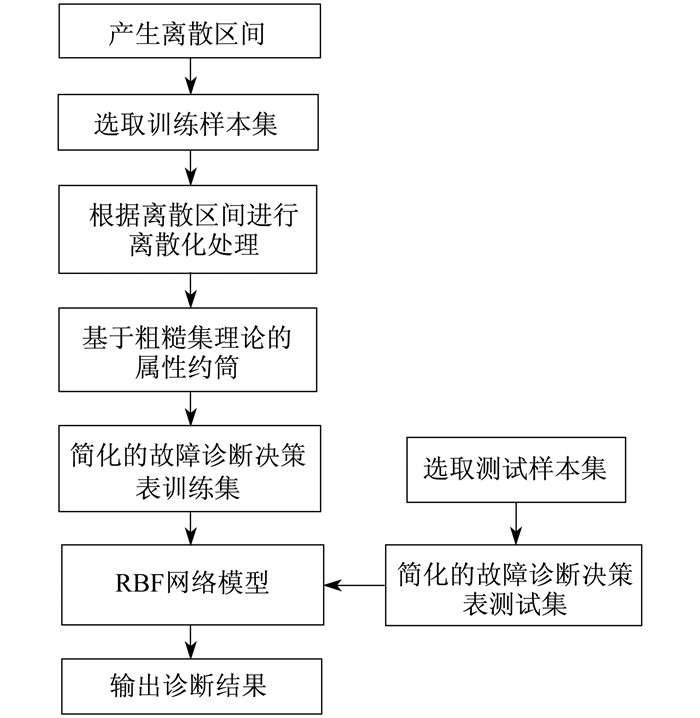
本文对燃气轮机控制系统传感器进行故障诊断, 主要是利用改进的等频离散化方法先对燃气轮机控制系统传感器的故障数据进行预处理, 得到离散化后的故障数据, 再用粗糙集对故障数据进行约简, 寻找属性间的关系, 从而简化神经网络的网络结构。图 2所示是基于改进等频离散化方法的粗糙集神经网络故障诊断流程。
其具体实现步骤为:
(1) 将燃气轮机控制系统传感器故障数据利用改进等频离散化方法进行离散化处理, 将各个故障征兆中的值按照升序排列并消除重复数据, 根据各个条件属性中值的数量分别确定区间k的数量, 以此得到各个故障征兆的离散区间;
(2) 从传感器故障数据中随机产生训练样本集与测试样本集, 并根据得到的离散区间分别对它们进行离散化, 得到离散化后的条件属性;
(3) 利用粗糙集理论消除与故障类型关联度低的条件属性, 简化传感器故障诊断样本;
(4) 将简化的训练样本集输入到RBF神经网络中进行训练, 并将训练好的网络进行保存;
(5) 用简化的测试样本集对训练好的RBF神经网络进行测试, 并输出诊断结果。
燃气轮机控制系统传感器按照故障原因可以分为偏差故障、冲击故障、漂移故障和周期性干扰故障。4种故障描述如表 1所示。
表 1
4种传感器故障类型及特征
| 故障类型 | 故障描述 |
| 偏差故障 | 在原信号的基础上叠加恒定的小信号 |
| 冲击故障 | 在原信号的基础上加上叠加一个脉冲信号 |
| 漂移故障 | 信号以某一速率偏移原信号 |
| 周期性干扰故障 | 原信号上叠加某一频率的周期性信号 |
本文以燃气轮机压气机进气温度传感器为例进行故障诊断, 选取在某一负荷下传感器处于上述4种状态及正常状态时, 整个控制系统中各种参数(如压气机排气温度、压气机进气压力等)的数据作为故障征兆属性, 进行温度传感器的故障诊断。分别对燃气轮机传感器正常状态和4种故障状态进行编码, 作为故障决策表的决策属性和神经网络的输出。表 2列出了其对应关系。表 3为故障征兆属性编码对应的各种测量参数名称。
表 2
传感器状态类型及编码
| 传感器状态类型 | 决策属性 | |||
| D1 | D2 | D3 | D4 | |
| 正常 | 0 | 0 | 0 | 0 |
| 偏差故障 | 1 | 0 | 0 | 0 |
| 冲击故障 | 0 | 1 | 0 | 0 |
| 漂移故障 | 0 | 0 | 1 | 0 |
| 周期性干扰故障 | 0 | 0 | 0 | 1 |
表 3
测量参数与故障征兆属性对应关系
| 故障征兆属性编码 | 测量参数名称 |
| A1 | 压气机进气温度 |
| A2 | 压气机进气压力 |
| A3 | 压气机排气温度 |
| A4 | 透平排气温度 |
| A5 | 燃气流量 |
| A6 | 发电机功率 |
随机选取其中的300组数据, 其中240组作为训练样本集, 60组作为测试样本集, 其部分故障诊断决策如表 4所示。
表 4
传感器故障诊断决策表
| A1 | A2 | A3 | A4 | A5 | A6 | D1 | D2 | D3 | D4 |
| 85.1 | 0.88 | 579.9 | 1 032.7 | 7.41 | 40.83 | 0 | 0 | 0 | 0 |
| 86.2 | 0.91 | 580.3 | 1 033.1 | 7.34 | 40.71 | 1 | 0 | 0 | 0 |
| 91.1 | 0.98 | 581.4 | 1 033.7 | 7.65 | 41.93 | 0 | 1 | 0 | 0 |
| 87.4 | 0.92 | 580.3 | 1 032.9 | 7.36 | 40.91 | 0 | 0 | 1 | 0 |
| 88.3 | 0.95 | 580.7 | 1 033.8 | 7.39 | 41.23 | 0 | 0 | 0 | 1 |
利用改进的等频离散化方法对故障数据进行离散化处理。根据离散区间可以得到离散化后的训练样本集故障决策表, 部分数据如表 5所示。
表 5
传感器故障诊断决策表中的部分数据
| C1 | C2 | C3 | C4 | C5 | C6 | D1 | D2 | D3 | D4 |
| 3 | 4 | 6 | 4 | 5 | 4 | 0 | 0 | 0 | 0 |
| 5 | 5 | 7 | 5 | 4 | 3 | 1 | 0 | 0 | 0 |
| 13 | 9 | 10 | 6 | 8 | 9 | 0 | 1 | 0 | 0 |
| 7 | 5 | 7 | 5 | 4 | 5 | 0 | 0 | 1 | 0 |
| 9 | 6 | 8 | 6 | 5 | 7 | 0 | 0 | 0 | 1 |
利用RS理论对离散化后的训练集故障决策表的条件属性进行约简, 约简后的部分结果如表 6所示。
表 6
属性约简后的传感器故障诊断决策表
| C1 | C3 | C4 | C5 | D1 | D2 | D3 | D4 |
| 3 | 6 | 4 | 5 | 0 | 0 | 0 | 0 |
| 5 | 7 | 5 | 4 | 1 | 0 | 0 | 0 |
| 13 | 10 | 6 | 8 | 0 | 1 | 0 | 0 |
| 7 | 7 | 5 | 4 | 0 | 0 | 1 | 0 |
| 9 | 8 | 6 | 5 | 0 | 0 | 0 | 1 |
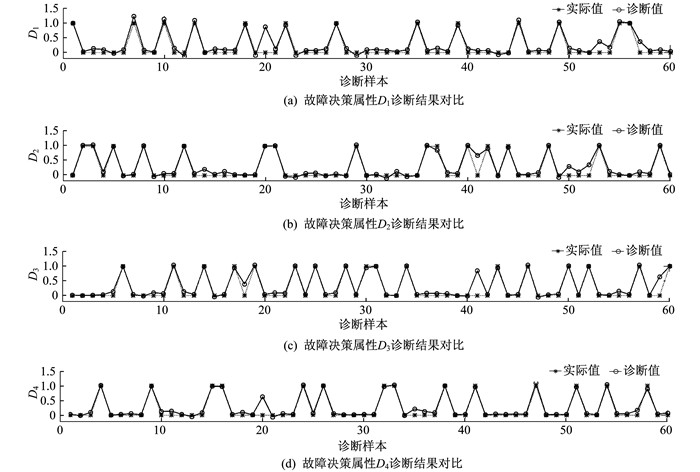
将选取的测试集样本进行离散化和属性约简, 并输入到已经训练好的RBF神经网络中。故障诊断结果和故障类型的对比曲线如图 3所示。
分别采用RBF神经网络方法和RS-RBF神经网络方法对燃气轮机控制系统的传感器进行故障诊断, 可以得到2种方法的诊断准确率和诊断绝对误差, 如表 7所示。
表 7
3种诊断方法的比较
| 方法 | 网络结构 | 诊断率/% | 平均绝对误差 |
| RBF | 6-10-4 | 85.00 | 0.127 6 |
| RS-RBF | 4-9-4 | 93.30 | 0.094 2 |
| 改进等频离散化RS-RBF | 4-9-4 | 96.70 | 0.078 2 |
由表 7中可以看到, 运用RS可以简化神经网络的网络结构, 提升诊断率, 这是因为RS可以对条件属性进行约简, 简化故障诊断规则。改进等频离散化RS-RBF的故障诊断准确率和精度更高, 这是因为改进的等频离散化方法通过消除重复值, 解决了两个相同大小的数据被分到不同区间的问题, 避免破坏故障诊断规则, 有利于粗糙集对故障诊断规则的提取。此外, 通过设定区间数k的取值方法, 解决了k值过大不利于有效提取故障诊断规则和k值过小丢失故障诊断规则的问题, 使得RS能够对故障规则进行有效的提取, 进而得到完整的故障诊断规则。
4 结语
(1) RS理论可以有效地对条件属性进行约简, 简化神经网络的网络结构, 相比于单纯的RBF神经网络, 诊断的准确率有所提高, 并且减小了诊断的误差;
(2) 采用改进的等频离散化方法提高了故障诊断的准确率并且减小了故障诊断的误差, 由此证明了该方法的可行性, 可以在故障诊断领域中得到良好的应用。
参考文献
-
[1]李树田. 国内大型燃气轮机发展历程及运行综述[J]. 浙江电力, 2012, 31(12): 75-78.
-
[2]徐含灵. 燃气轮机控制系统传感器故障诊断与信号重构方法研究[D]. 北京: 中国科学院大学, 2019.
-
[3]贾宝柱, 贾志涛, 余培文, 等. 数据驱动的船舶智能故障诊断方法[J]. 控制工程, 2019, 26(10): 1892-1898.
-
[4]张成军, 阴妍, 鲍久圣, 等. 多源信息融合故障诊断方法研究进展[J]. 河北科技大学学报, 2014, 35(3): 213-221.
-
[5]袁海满, 吴广宁. 基于多信息融合的变压器故障诊断[J]. 高压电器, 2018, 54(9): 103-110.
-
[6]CAO J, ZHANG X, ZHANG C, et al. Improved convolutional neural network combined with rough set theory for data aggregation algorithm[J]. Journal of Ambient Intelligence & Humanized Computing, 2020, 11(2): 647-654.
-
[7]JAHANGIR H, TAYARANI H, BAGHALI S, et al. A novel electricity price forecasting approach based on dimension reduction strategy and rough artificial neural networks[J]. IEEE Transactions on Industrial Informatics, 2019, 16(4): 2369-2381.
-
[8]谢玲玲, 雷景生, 徐菲菲. 基于改进的邻域粗糙集与概率神经网络的水电机组振动故障诊断[J]. 上海电力学院学报, 2016, 32(2): 181-187.
-
[9]桑雨. 连续数据离散化方法研究[D]. 大连: 大连理工大学, 2012.
-
[10]CEBECI Z, YILDIZ F. Unsupervised discretization of continuous variables in a chicken egg quality traits dataset[J]. Turkish Journal of Agriculture-Food Science and Technology, 2017, 5(4): 315-320. DOI:10.24925/turjaf.v5i4.315-320.1056
-
[11]SIVASANKAR E, SELVI C, MAHALAKSHMI S. Rough set-based feature selection for credit risk prediction using weight-adjusted boosting ensemble method[J]. Soft Computing, 2020, 24(6): 3975-3988. DOI:10.1007/s00500-019-04167-0
-
[12]林琳, 陈志英. 基于粗糙集神经网络和振动信号的高压断路器机械故障诊断[J]. 电工技术学报, 2020, 35(增刊1): 277-283.