|
|
|
发布时间: 2021-02-25 |
智能电网技术 |
|
|
|
收稿日期: 2020-03-24
中图法分类号: TM733
文献标识码: A
文章编号: 2096-8299(2021)01-0031-06
|
摘要
对微电网线路故障的高效检测有助于快速切除故障,降低微电网对大电网的影响。现有的故障检测方法存在阈值难以选择、对高过渡电阻故障不敏感等问题,为此提出了基于极大重叠离散小波变换(MODWT)系数突变的自适应阈值选取故障检测算法。利用MODWT的特性,采用扩大窗的方法,在窗扩大的过程中对MODWT系数差值的阈值进行适应性调整。相较于现有的定阈值方法,该算法可以适应任意长度的数据样本,对于多种故障状态可以进行适应性阈值调整,因此对高过渡电阻故障有较高的敏感度。通过仿真实验验证,该算法能在各种故障状态下快速检测故障发生的时间。
关键词
微电网; 故障检测; 极大重叠离散小波变换; 自适应阈值
Abstract
Efficient detection of microgrid line faults helps to quickly remove the fault and reduce the impact on the large power grid.Existing fault detection methods have problems such as difficulty in selecting thresholds and insensitivity to high transition resistance faults.The proposed adaptive threshold selection fault detection method based on sudden changes of MODWT coefficients uses the characteristics of MODWT and adopts the method of expanding the window to adaptively adjust the threshold of the MODWT coefficient difference during the process of window expansion.Compared with the existing threshold method, the method proposed can adapt to data samples of any length, and can adjust the adaptive threshold for various fault conditions, so it has a higher sensitivity to high transition resistance faults.Through simulation verification, this method can quickly detect the time of failure in various fault states.
Key words
microgrid; fault detection; maximal overlap discrete wavelet transfrom; adaptive threshold
微电网是一种小规模的含分布式电源的独立供电系统[1]。若在并网状态下发生故障, 不仅会影响自身供电, 还会对大电网的稳定运行产生一定的干扰, 严重时会造成大规模的停电事故以及大
量设备的损坏[2]。因此, 准确高效的故障检测手段是电网安全运行的重要保证。传统的电网故障诊断方法是通过对比故障前后各种电气量信息、保护动作和断路器动作的开关量变化, 以这些信息为依据对故障进行检测、定位和分类[3]。随着微电网的发展, 对故障检测方法的可靠性和及时性要求越来越高, 面对复杂的故障状态, 传统的故障检测方法难以满足要求, 因此需要选取合适的数据和分析方法, 以保证微电网故障检测的准确性和高效性[4]。文献[5]提出了基于希尔伯特-黄变换的微电网内部故障检测方法, 通过对电压数据作希尔伯特-黄变换处理和分析, 得到了监测点相应的本征模态函数、瞬时振幅、瞬时频率、时频幅值谱及边际谱, 根据电压信号时频幅值谱及边际谱综合判定故障是否发生。文献[6]提出了基于改进的粒子群优化的径向基神经网络, 提高了输电网络故障检测的准确率, 选取电压等电气量作为特征, 设置故障样本训练网络, 用训练好的网络对故障进行检测。文献[7-9]提出了利用小波分析检测分布式电网输电线路故障, 通过提取故障电压的高频信息, 以高频小波系数作为特征, 能够直观地区分正常和故障情况。
小波变换作为时频分析的重要工具, 能够对微电网发生故障时的频率突变现象进行有效的描述, 适用于微电网线路故障分析, 但现有的定阈值方法存在阈值难以选择以及对高过渡电阻故障不敏感的问题, 在多种故障状态下难以发挥作用。本文提出了基于极大重叠离散小波变换(Maximal Overlap Discrete Wavelet Transfrom, MODWT)邻近系数差的自适应阈值选取方法, 设定窗长度和扩大步长, 在窗扩大的过程中对窗内电压进行MODWT, 提取高频分段的系数, 并利用MODWT相邻样本点系数差的大小对阈值不断进行调整, 将调整后的阈值作为依据来判断故障是否发生。通过MATLAB/Simulink建立基于IEEE标准13节点传输线路的微电网, 设定不同的故障类型、故障情况以及随机故障时间点, 取得故障原始电压数据, 并用所提方法对故障样本进行分析和仿真验证。
1 离散小波变换
小波变换是一种对信号进行时频分析的工具。小波变换以小波函数为基函数, 通过小波基函数的平移和伸缩将信号映射到时间-尺度(频率)平面, 分别对信号的时间信息和频率信息进行描述。
小波变换在工程学科中的应用以离散小波变换为主。离散小波变换(Dicrete Wavelet Transform, DWT)的公式[10]为
| $ {\mathop{\rm DWT}\nolimits} (m, n) = \frac{1}{{\sqrt {a_0^m} }}\sum\limits_k s (k)\psi \left( {\frac{{k - n{b_0}a_0^m}}{{a_0^m}}} \right) $ | (1) |
式中: DWT(m, n)——时刻n和尺度m下的小波系数;
a0m——缩放因子, 其中a0=2;
s(k)——原信号;
k——离散后的时间;
ψ(·)——小波基函数;
nb0——平移因子, 其中b0=1。
Mallat算法的公式[10]为
| $ {S_{j + 1, k}} = \sum\limits_{n = 0}^{l - 1} {{S_{j, n}}} {g_{n - 2k}} $ | (2) |
| $ {T_{j + 1, k}} = \sum\limits_{n = 0}^{l - 1} {{S_{j, n}}} {h_{n - 2k}} $ | (3) |
式中: Sj, Tj——不同分辨率下的近似系数和细节系数;
gn, hn——低通滤波器和高通滤波器。
MODWT在金融数据分析[11]和脑电波信号分析[12]方面具有广泛的应用。与DWT不同, MODWT的低通和高通滤波器可分别表示为
| $ {{\tilde S}_{j + 1, k}} = \sum\limits_n {{{\tilde g}_n}} {{\tilde S}_{j, k - n\, \bmod \, N}} $ | (4) |
| $ {{\tilde T}_{j + 1, k}} = \sum\limits_n {{{\tilde h}_n}} {{\tilde S}_{j, k - n\, \bmod \, N}} $ | (5) |
式中:
N——离散信号的长度。
与DWT相比, MODWT具有以下特性: 系数平移不变性, 当信号平移时, MODWT系数不会因为信号的移动而改变; 没有降采样过程, 保持了系数的完整性, 避免了重要信息的缺失, 其变换系数的样本长度与原信号的样本长度一致, 适用于信号异常发生点的精准检测; 可以对任意长度的信号进行处理, 对样本个数没有要求, 适用性范围更广; 基于MODWT的多分辨率分析可以对数据进行方差分析[13]。
本文主要利用了MODWT每级分解都保持系数与原始数据长度相等的特性, 以保证故障时间检测的准确性。
2 基于MODWT系数突变自适应阈值的故障检测
2.1 故障特征提取
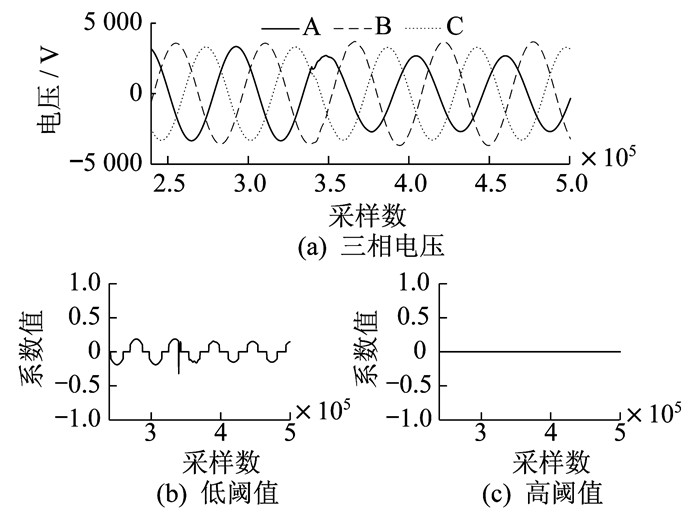
当微电网发生故障时, 电压会发生突变, 产生短暂的高频分量。通过多分辨率分析可以将故障电压分解到不同的频带。本文选用Haar小波作为基函数, 分析所提取的高频系数、有效识别故障, 并对故障时间进行检测。此时的电压波形和A相电压一级细节系数如图 1所示。
由图 1(b)和图 1(c)可以看出, DWT和MODWT都可以得到故障电压的高频分量, 实现故障检测, 但DWT无法对故障时间进行精确定位。DWT经过降采样后, 去除了一半的系数, 因此造成系数突变部分与故障发生部分存在时间差。由此可见, MODWT更适用于故障时间的检测。本文采用Haar小波对故障电压进行MODWT, 选取一级细节系数作为故障特征。
2.2 故障检测算法
文献[8]提出了一种模极值法, 首先对电压进行小波变换, 得到高频分段的系数, 然后设定一个阈值, 超过此阈值的系数就识别为故障发生时刻。此方法存在阈值难以选择的问题: 若阈值设定过高, 则可能会丢失故障点, 导致识别失败; 若阈值设定过低, 则会因出现多个超过阈值的点导致误报警。上述情况如图 2所示。
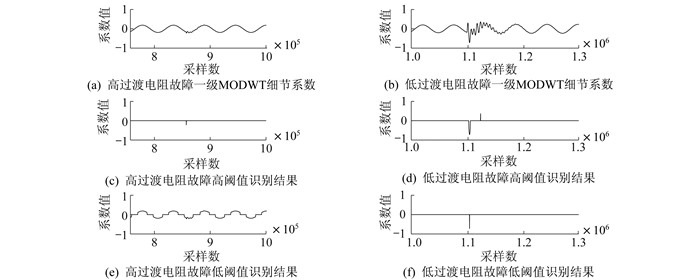
此外, 由于难以设定合适的阈值, 模极值法无法同时识别高、低过渡电阻故障, 不同情况下的识别结果如图 3所示。当阈值设定过高时, 低过渡电阻故障可能识别失败; 当阈值设定过低时, 高过渡电阻故障可能识别失败。
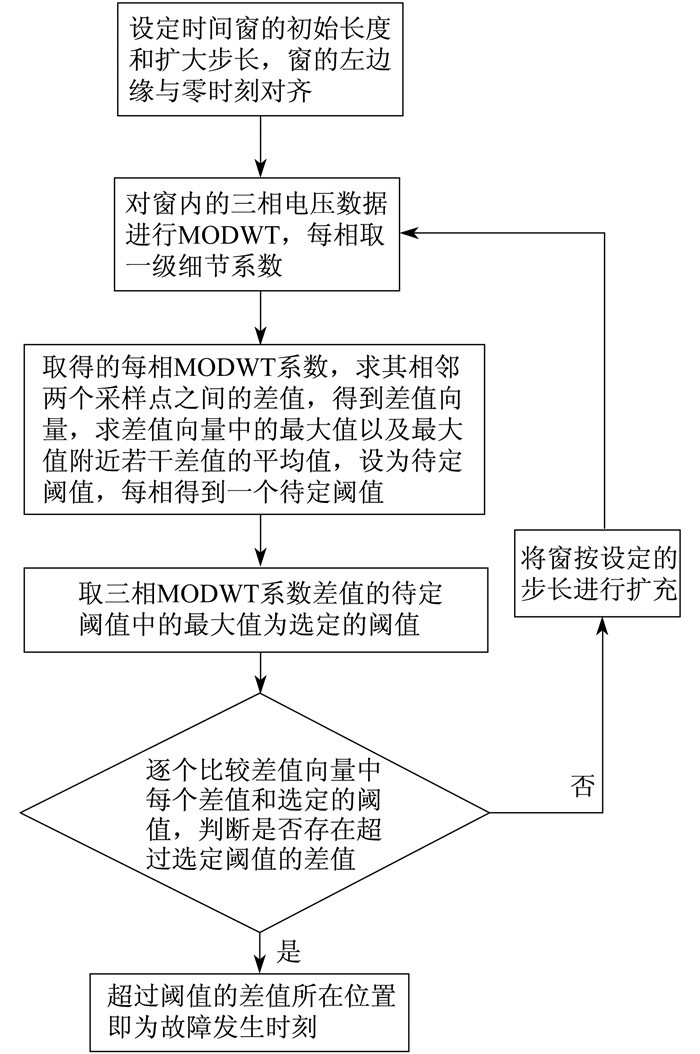
文献[9]提出了一种利用滑动窗小波变换对故障进行检测的方法。首先, 通过滑动窗检测电流电压的大幅度变化来确定故障发生的大概时间段; 然后, 对检测到的窗内数据进行小波变换, 并利用模极值法检测具体的故障时刻。该方法适用于直流输配电系统的故障检测, 对于交流微电网系统, 通过检测电流和电压的大幅度变化来确定故障发生时段的方法并不合适。但其时间窗的思路是可取的, 通过设定时间窗的宽度和滑动步长, 可以保证故障检测的及时性, 确保故障发生后及时切除。因此, 本文提出了一种基于MODWT系数突变的自适应阈值选取故障检测方法。通过设定时间窗, 对窗内电压数据进行MODWT, 求得一级细节系数相邻点的差值, 根据差值绝对值的极值及其周围若干系数差值对阈值进行调整, 再利用调整后的阈值检测窗内是否发生故障。每次时间窗扩大时, 都会得到新的阈值, 直到检测出窗内出现故障。算法流程如图 4所示。
扩大窗的初始长度和扩大步长是预先设定的, 初始状态窗左端与零时刻对齐。扩大过程中, 左端不变, 右端按步长增加。采用的扩大窗是对微电网实时检测的模拟。微电网初始运行时间相当于时间窗的初始长度, 当窗内未发现故障时, 继续扩大步长的长度进行检测, 直到窗内检测到故障发生。相比于滑动窗, 扩大窗能避免大量的电压数据边缘系数突变的干扰。滑动窗每次滑动, 都会产生干扰现象, 这个边缘产生的干扰可能覆盖故障部分, 导致故障部分被忽略; 而扩大窗能够有效避免这种情况, 只需将窗两端的系数突变的干扰现象平均化, 当求得系数的邻近系数差时, 将干扰部分的系数差规定为窗内整体系数差值的平均值, 这样突变部分就不会因为超过阈值而被误识别。根据本文情况, 系数干扰部分为500个采样数以下, 因此对窗两端内侧500个采样点的系数差值进行平均化操作。
与模极值法不同, 本文所提出的故障检测算法取决于系数是否发生突变, 即相邻系数差的绝对值是否超过所选阈值, 而非系数绝对值是否超过所选阈值。相邻系数差的绝对值可以表示为
| $ {D_k} = \left| {{{\tilde T}_{1, k + 1}} - {{\tilde T}_{1, k}}} \right| $ | (6) |
式中:
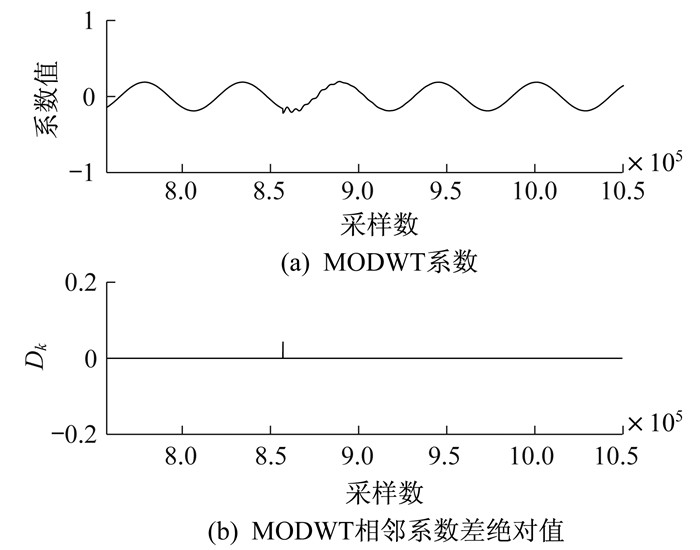
选用系数是否突变作为故障是否发生的依据, 可以有效解决高过渡电阻故障阈值难以选择的问题。一级MODWT细节系数值和系数相邻两点差值的绝对值曲线如图 5所示。
由图 5可以看出, 对于高过渡电阻故障, 发生故障时的系数值与故障前正常部分的系数值存在重叠现象, 没有明显超出正常阈值的现象, 难以设定合适的阈值来判断故障是否发生; 而故障发生后的系数差值有明显突变现象, 此时可以较为容易地选取阈值来作为判断依据。
与文献[7-8]中设定的固定阈值不同, 本文采用自适应的阈值确定法。当扩大窗不断扩大时, 每扩大一步, 阈值就会根据窗中电压数据MODWT系数的差值进行调整, 得到新的阈值, 直到检测出故障发生。此时, 取得最合适的阈值, 检测到窗内发生故障, 并进行故障时间定位。通过求系数差值绝对值的最大值附近若干点的平均值对阈值进行调整, 公式为
| $ {D_{{\rm{threshold }}}} = \frac{1}{{2a + 1}}\sum\limits_{k = {k_{\max }} - a}^{{k_{\max }} + a} {{D_k}} $ | (7) |
式中: Dthreshold——调整后的阈值;
a——所取前后点的个数;
kmax——相邻系数差值的绝对值最大的位置;
Dk——相邻系数之间的差值。
当系数的绝对差值超过阈值时, 故障发生。这一判断过程可表示为
| $ \left\{ {\begin{array}{*{20}{l}} {{L_k} = 1}&{{D_k} \ge {D_{{\rm{threshold }}}}}\\ {{L_k} = 0}&{{D_k} < {D_{{\rm{threshold }}}}} \end{array}} \right. $ | (8) |
故障状态存在多样性, 即使同一地点发生的故障, 由于故障发生时间(初相位)、故障类型、过渡电阻不同, 设定固定的阈值也无法实现准确检测, 尤其是高过渡电阻故障时, 故障时刻的MODWT系数值接近正常状态的系数值, 因此无法确定一个适用于所有故障情况的阈值。采用相邻系数差值为特征以及采取自适应调整阈值的方法, 能够有效解决上述问题, 下面通过案例分析验证所提方法的有效性。
3 案例分析
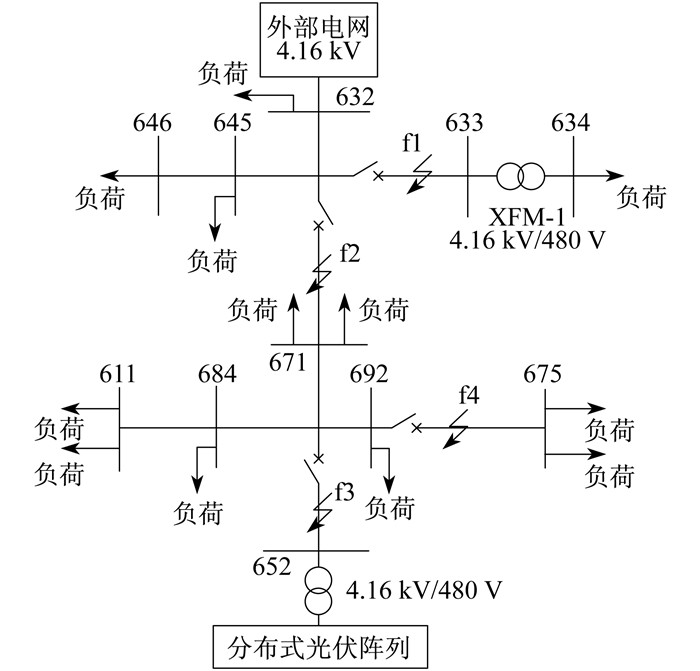
本文采用的微电网是基于IEEE标准13节点传输网络, 工频设定为60 Hz, 采样频率为3.33×106 Hz, 在传输网络680总线处设置分布式电源, 模型结构如图 6所示。该系统是一个不平衡的4.16 kV馈线系统。微电网分布式电源为光伏阵列, 光伏系统采用最大功率点跟踪控制, 通过逆变装置、变压器以及传输线路与大电网连接, 实现并网。
在MATLAB/Simulink中搭建微电网系统, 并设置不同的故障工况。通过设置不同的故障地点、故障类型、故障过渡电阻以及随机故障发生时刻, 获得故障的电压数据。故障变量设置如下: 故障区域为图 6中的f1, f2, f3, f4;故障类型主要为线路的短路故障, 对于A相、B相、C相和接地G, (A B C)G为单相接地短路, AB, AC, BC为两相短路, 以此类推, 共有11种短路故障; 故障过渡电阻为0.01 Ω, 1 Ω, 50 Ω; 故障发生时刻(t1, t2, t3)设置为随机, 保证了故障初相角的随机性。
此方法在识别过程中会存在一定的延时, 延时主要取决于窗的扩大步长。本文中的时间窗初始长度为0.01 s, 扩大步长为0.002 5 s。所取前后点的个数a=20。
通过大量仿真实验, 与模极值法相比, 本文所提出的方法对各种故障类型都。仿真实验结果如表 1所示。
表 1
故障检测算法的仿真实验结果对比
| 统计量 | 模极值法(高阈值) | 模极值法(低阈值) | 自适应阈值选取法 | |||||
| 高过渡电阻 | 低过渡电阻 | 高过渡电阻 | 低过渡电阻 | 高过渡电阻 | 低过渡电阻 | |||
| 故障样本数/个 | 132 | 264 | 132 | 264 | 132 | 264 | ||
| 检测成功/个 | 37 | 230 | 10 | 264 | 131 | 264 | ||
| 误报警/个 | 5 | 0 | 122 | 0 | 1 | 0 | ||
| 检测失败/个 | 90 | 34 | 0 | 0 | 0 | 0 | ||
| 成功率/% | 28.03 | 87.12 | 7.58 | 100.00 | 99.24 | 100.00 | ||
由表 1可以看出, 模极值法选取高阈值时, 对低过渡电阻故障的检测准确率较低; 选取低阈值时, 对低过渡电阻故障的检测准确率会有显著上升, 但高过渡电阻故障检测准确率会降低; 无论选取高阈值还是低阈值, 高过渡电阻故障的准确率都非常不理想。本文提出的基于MODWT系数突变的自适应阈值选取故障检测算法对于高、低过渡电阻故障, 都具有较高的敏感性, 检测准确率均较高。
4 结语
本文提出的基于MODWT系数突变的自适应阈值选取故障检测算法对于微电网线路短路故障有较好的检测效果, 对高过渡电阻故障也有较高的敏感性。其中, 扩展窗能够有效避免因大量的数据边缘系数突变的干扰而导致的故障时间点丢失现象, 在时间窗的扩大过程中不断调整阈值。该算法适用于多种故障, 且对于高过渡电阻故障也能选取合适的阈值进行故障检测和定位。
本文只针对微电网的线路短路故障, 微电网的其他线路故障还有很多, 如断路、断路点电弧、绝缘击穿等; 故障类型除了线路故障, 还包括分布式电源内部故障、变压器故障、元器件故障等。本文算法对其他类型故障以及多故障并发等情况的有效性仍有待进一步验证。
参考文献
-
[1]王颖, 唐函侃, 潘明九. 基于小波变换的微电网故障检测方法设计[J]. 内燃机与配件, 2017(8): 90-92. DOI:10.3969/j.issn.1674-957X.2017.08.047
-
[2]屈克庆, 葛海锋, 孔玮. 分布式光伏发电系统对配电网电压的影响分析[J]. 上海电力学院学报, 2019, 35(3): 201-204. DOI:10.3969/j.issn.1006-4729.2019.03.001
-
[3]刘仲民, 呼彦喆, 张鑫. 电网故障智能诊断技术研究综述[J]. 南京师大学报(自然科学版), 2019, 42(3): 138-144. DOI:10.3969/j.issn.1001-4616.2019.03.018
-
[4]刘鹏磊. 微电网故障特性分析及保护策略的研究[D]. 湘潭: 湘潭大学, 2018.
-
[5]王颖. 微电网故障检测方法及保护原理研究[D]. 杭州: 浙江大学, 2017.
-
[6]张淑卿, 李卓桐, 张立红. 改进PSO-RBF神经网络的电网故障检测模型[J]. 计算机时代, 2019(1): 5-8.
-
[7]方登洲, 张帆, 侯巍, 等. 基于离散小波变换的输电线路故障检测研究[J]. 信息技术, 2019(10): 110-114.
-
[8]SILVA K M, SOUZA B A, BRITO N S D. Fault detection and classification in transmission lines based on wavelet transform and ANN[J]. IEEE Transactions on Power Delivery, 2006, 21(4): 2058-2063. DOI:10.1109/TPWRD.2006.876659
-
[9]CHANG C S, KUMAR S, LIU B. Real-time detection using wavelet transform and neural network of short-circuit faults within a train in DC transit systems[J]. IEE Proceedings-Electric Power Applications, 2001, 148(3): 251-256. DOI:10.1049/ip-epa:20010350
-
[10]ADDISON P S. The illustrated wavelet transform handbook[M]. Bristol: Institute of Physics Publishing, 2002: 93-117.
-
[11]董洋, 李洁, 杨莉. 国内外金属期货市场间的动态联动以及多尺度特征研究——基于时频视角分析[J]. 昆明理工大学学报(自然科学版), 2019, 44(2): 127-136.
-
[12]李东明, 王典洪, 严军, 等. 基于MODWT的运动想象脑电信号识别[J]. 计算机工程, 2014, 40(10): 161-167.
-
[13]PERCIVAL D B, WALDEN A T. Wavelet methods for time series analysis[M]. Cambridge, UK: Cambridge University Press, 2000: 162-173.