|
|
|
发布时间: 2021-02-25 |
智能电网技术 |
|
|
|
收稿日期: 2020-03-24
基金项目: 上海市地方能力建设项目(14110500900)
中图法分类号: TM935.2
文献标识码: A
文章编号: 2096-8299(2021)01-0027-04
|
摘要
针对现有电压暂降评估方法忽略了配电网综合负荷特性对评估结果影响的问题,分析了电力系统设备用户端负荷特性对电压暂降特征值的影响。结合设备用户端的综合负荷模型以及实际配电网中的电压暂降波形,通过实际案例进行了电压暂降仿真分析,结果验证了大型感应电机接入母线处电压暂降的特征。
关键词
电压暂降; 负荷特性; 特征值; PSCAD
Abstract
Aiming at the problem that the existing voltage sag ignores the influence of the user load characteristics on the assessment results, the influence of the distribution network's comprehensive load characteristics on the voltage sag characteristic values is analyzed.Combined with the comprehensive load model of the equipment client and the voltage sag waveform in the actual distribution network, and through the simulation analysis of the actual cases, the characteristics of the voltage sag at the bus connection of large induction motor are verified.
Key words
voltage sag; load characteristics; characteristic value; PSCAD
现代新型负荷对电能质量的要求越来越严格, 对供电可靠性的需求也越来越高, 因此对电压暂降事件非常敏感[1]。另一方面, 电能传输的特殊性导致电能质量不完全取决于电力企业, 电压暂降也与用户内部电网以及用户负荷性质有关[2]。
在过去的一些电压暂降研究中, 假设电压在短路发生瞬间立即下降到最低幅值, 故障切除后电压立即恢复, 即矩形暂降。结合典型电压暂降场景, 将负荷等效为恒阻抗等值模型。但是, 实际系统发生短路故障瞬间, 不同的负荷具有不同的电压暂降特性, 而以上的假设并未考虑感应电动机等动态负荷对实际电压暂降波形的影响[3-4]。由于忽略
了用户终端动态负荷特性, 因此不能得到合理的分析评估结果。文献[3]在进行电压暂降评估时, 将系统中所有负载都假设用一个恒阻抗模型代替。文献[4]中故障引起的电压暂降和由初级保护清除的电压暂降被认为是忽略了负载动态而形成的矩形暂降。
虽然已有文献研究了感应电动机启动及运行时对电压暂降特性的影响[5-6], 但要进一步开展相关评估的研究, 还有必要考虑设备用户端的负载特性对电压暂降特征值的影响, 以便对实际电压暂降的特征值进行准确的界定。
针对电压暂降特征分析和评估的不足, 本文以实际电网为研究对象, 结合配电网中感应电动机负荷的分布, 利用PSCAD仿真工具建立仿真模型, 对比不同用户的负荷特性对电压暂降波形的影响, 并描述电压暂降特征值, 为后续更准确地获得设备终端的电压暂降特征提供仿真依据。
1 设备用户端的综合负荷模型
电力系统综合负荷模型是反映实际电力系统的频率f、电压u、时间t特性的负荷模型。一般表达式[7]为
| $ \left\{ {\begin{array}{*{20}{l}} {P = {f_p}(u, f, t)}\\ {Q = {f_q}(u, f, t)} \end{array}} \right. $ | (1) |
式中: P, Q——系统中的有功功率和无功功率;
fp(·), fq(·)——有功功率和无功功率的表达式。
式(1)中含有时间t, 则反映综合负荷的动态特性, 反之称为静态负荷模型。
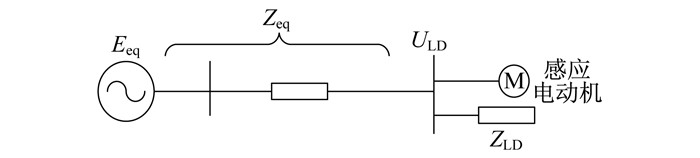
负荷模型的选择在很大程度上影响着电压暂降的分析结果。配电网中, 感应电动机负荷约占总电力负荷的60%, 在电力系统暂态稳定计算中, 动态负荷模型常用感应电动机模型表示[8]。电力系统的综合负荷常用一个感应电动机负荷并联等值恒阻抗模型来模拟, 单机综合负荷供电系统如图 1所示。其中, Eeq为系统的三相等效电源, zeq为线路等值阻抗, ULD为负荷母线处电压, ZLD为负荷阻抗值。
随着对电压暂降机理的深入研究, 感应电动机等动态负荷对电压稳定的影响逐步得到重视。考虑用户终端动态负荷特性时, 随着电压暂降的发生, 感应电动机会为配电网提供无功功率支持。而且大型高压电机有可能提供更高的无功支持, 提供无功功率的持续时间更长, 以防止电压的快速崩溃。因此, 电压响应不会直接降到幅值最低处, 进而改变电压暂降波形。
2 电压暂降典型波形的分析
电压暂降描述为电网中突然出现数倍甚至数十倍于额定值的大电流, 在系统阻抗上的分压增大, 造成公共连接点(Point of Common Coupling, PCC)点电压突然降低。系统内突然出现大电流原因有很多: 系统侧原因包括短路故障、大型变压器空载激磁等; 用户侧原因包括大容量感应电动机启动、大负荷投切等。考虑其在配电网中传播以及动态负荷对故障清除后电压暂降恢复的影响, 徐永海等人以264次有效电压暂降事件为研究样本, 按不同电压等级将常见电压暂降波形监测统计, 具体如表 1所示。
表 1
不同电压等级下典型波形对应的暂降概率
| 均方根值波形 | 电压等级 | |||
| 10 kV | 35 kV | 110 kV | 220 kV | |
| 矩形波 | 59.35 | 51.85 | 72.92 | 90.11 |
| 左快右慢型 | 12.26 | 40.74 | 23.96 | 4.40 |
| 左慢右快型 | 16.13 | 0 | 1.04 | 4.40 |
| 其他 | 12.26 | 7.41 | 2.08 | 1.10 |
由表 1可知: 第一类暂降是由故障引起的矩形波, 占比68.56%;而由电机启动不当或变压器励磁涌流造成的暂降, 属于左快右慢型, 占比20.44%;当短路故障在感应电动机附近时, 可能是左慢右快型, 且故障切除时间和电机参数很大程度上决定了波形形态, 这类暂降占比5.39%;还有其他类电压暂降如雷击造成的绝缘子闪络等不规则电压暂降波形, 占比5.71%。
3 仿真分析与算例验证
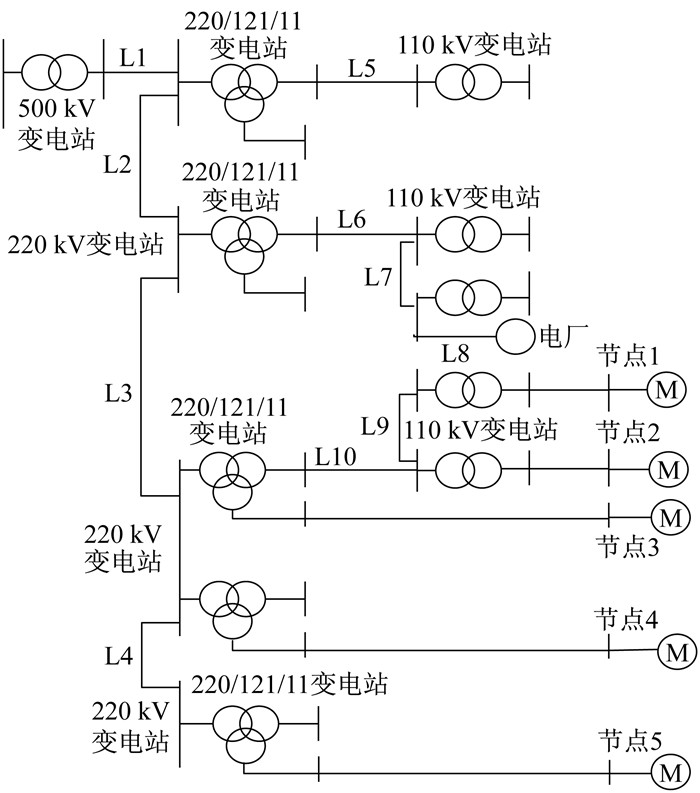
本文以某一高新技术企业为研究对象, 利用电力系统电磁暂态软件PSCAD建立电力系统仿真模型。系统将500 kV母线和110 kV电厂作为恒压源供电, 用户由2个220 kV变电站和2个110 kV变电站中的5条10 kV线路供电, 用户线路均为YJV-300的电缆。考察架空线路发生短路故障造成的用户电压暂降情况。
本文分别采用恒阻抗等值模型[9]和感应电动机并联恒阻抗负荷来模拟综合负荷两种负荷特性, 节点1~5作为用户评估节点。电力系统仿真模型如图 2所示。输电线路典型参数, 感应电动机参数和线路长度参数分别见表 2~表 4。
表 2
不同电压等级下的输电线路典型参数(每105 m)
| 参数 | 电压等级 | ||
| 110 kV | 220 kV | 330 kV | |
| 正序电感/mH | 141.2 | 127.4 | 105.1 |
| 零序电感/mH | 443.5 | 382.2 | 315.3 |
| 正序电阻/W | 10.05 | 7.05 | 4.64 |
| 零序电阻/W | 32.3 | 32.3 | 26.2 |
| 正序电容/μF | 0.61 | 0.86 | 1.113 |
| 零序电容/μF | 0.453 | 0.605 | 0.763 |
| 正序阻抗角/(°) | 78 | 80 | 82 |
| 零序阻抗角/(°) | 74 | 75 | 75 |
表 3
感应电动机参数
| 参数 | 数值 |
| 定子绕组电阻(p.u.) | 0.066 |
| 转子第一笼型电阻(p.u.) | 0.298 |
| 转子第二笼型电阻(p.u.) | 0.018 |
| 定子绕组漏抗(p.u.) | 0.046 |
| 定子不饱和励磁电抗(p.u.) | 3.860 |
| 转子不饱和互感抗(p.u.) | 0.122 |
| 第二笼型不饱和电抗(p.u.) | 0.105 |
| 惯性时间常数/s | 200.000 |
| 机械阻尼(p.u.) | 0.008 |
表 4
线路长度
| 线路 | 长度 |
| L1 | 10.00 |
| L2 | 7.70 |
| L3 | 3.90 |
| L4 | 5.00 |
| L5 | 3.45 |
| L6 | 3.90 |
| L7 | 5.90 |
| L8 | 2.00 |
| L9 | 2.50 |
| L10 | 2.90 |
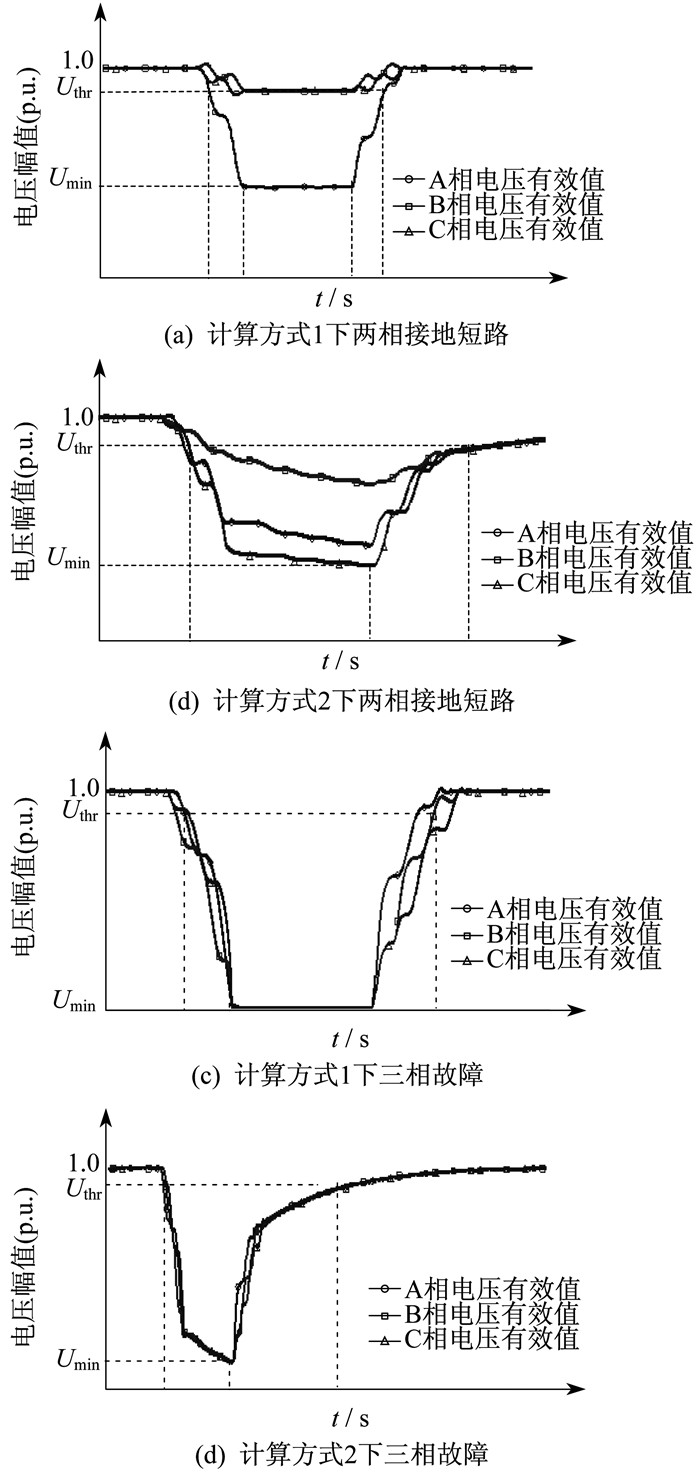
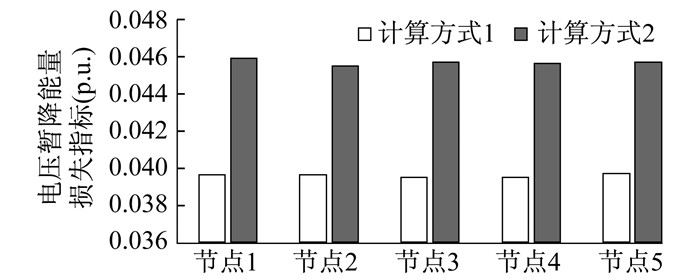
以线路L2发生两相接地故障和三相故障引起的电压暂降为例, 对负荷节点1~5处电压暂降情况进行仿真。各节点电压的方均根值波形变化如图 3所示。负荷节点1~5的电压暂降能量指标对比如图 4所示。其中, Uthr为电压暂降阈值电压, Umin为暂降过程中电压方均根值的最小值。
考虑到不同负荷特性对电压暂降的影响, 在仿真中选择两种计算方式。计算方式1指所有负荷节点均采用恒阻抗模型; 计算方式2指将负荷节点1~5采用综合负荷模型, 剩余节点采用恒阻抗模型。在相同计算方式下各节点电压波形大致相同, 为了便于对比, 以故障前节点的标称电压为基准值, 得到的仿真结果均以标幺值表示。
电压暂降常采用电压幅值和暂降持续时间来描述电压暂降特征。由图 3可知, 考虑感应电动机的综合负荷模型使得电压暂降波形变浅且变长, 即电压幅值更高, 电压暂降持续时间延长, 验证了上文中的分析。
由图 4可知, 节点电压暂降能量损失指标存在差异性, 这可以解释为感应电动机的动态响应为配电网提供了无功支持, 避免了电压快速崩溃, 但也导致电压暂降持续时间延长。电压暂降能量指标作为暂降严重度指标, 其值越大, 则侧面反映电压暂降越严重。
将采用两种计算方式仿真得到的电压暂降特征值进行对比, 结果如表 5和表 6所示。
表 5
两相接地短路故障时电压暂降特征值对比
| 节点 | 计算方式1 | 计算方式2 | |||
| 电压幅值(p.u.) | 持续时间/ms | 电压幅值(p.u.) | 持续时间/ms | ||
| 1 | 0.347 | 75.3 | 0.362 | 111.9 | |
| 2 | 0.332 | 75.7 | 0.352 | 112.1 | |
| 3 | 0.356 | 76.6 | 0.363 | 109.5 | |
| 4 | 0.340 | 76.2 | 0.357 | 110.2 | |
| 5 | 0.349 | 75.5 | 0.360 | 111.4 | |
表 6
三相短路故障时电压暂降特征值对比
| 节点 | 计算方式1 | 计算方式2 | |||
| 电压幅值(p.u.) | 持续时间/ms | 电压幅值(p.u.) | 持续时间/ms | ||
| 1 | 0.086 | 84.1 | 0.331 | 148.6 | |
| 2 | 0.086 | 84.7 | 0.332 | 149.8 | |
| 3 | 0.087 | 85.2 | 0.332 | 149.2 | |
| 4 | 0.083 | 85.3 | 0.328 | 148.3 | |
| 5 | 0.090 | 84.3 | 0.334 | 151.1 | |
由表 5和表 6可知, 采用综合负荷模型的计算方式2时, 较计算方式1得出的节点电压暂降的整体电压幅值更高, 持续时间更长。这是由于非矩形暂降在短时间内不会跌落至最低值, 并且恢复阶段更长; 而且也更体现感应电动机附近发生电压暂降的实际波形特征, 可以有效减小因忽略感应电动机负荷带来过度评估的影响, 使后续电压暂降的评估更具准确性和可信度。
4 结语
针对当前电力系统中的动态负荷主要以感应电动机为主的现实情况, 用感应电动机并联恒阻抗负荷来模拟综合负荷特性的实际情况。从系统角度分析得出感应电动机负荷有抗拒电压幅值突变的特性, 从而引起非矩形电压暂降的产生, 最终导致电压暂降特征值变化以及电压暂降能量损失增加。
参考文献
-
[1]刘旭娜, 肖先勇, 汪颖. 电压暂降严重程度及其测度、不确定性评估方法[J]. 中国电机工程学报, 2014, 34(4): 644-658.
-
[2]林海雪. 电能质量指标的完善化及其展望[J]. 中国电机工程学报, 2014, 34(29): 5073-5079.
-
[3]杨家莉, 刘书铭, 徐永海, 等. 基于熵权法的电压暂降严重程度综合评估方法[J]. 现代电力, 2017, 34(4): 40-49.
-
[4]肖先勇, 王希宝, 薛丽丽, 等. 敏感负荷电压凹陷敏感度的随机估计方法[J]. 电网技术, 2007(22): 30-33.
-
[5]孔祥启, 江友华, 付泽勋, 等. 基于PSAF电力系统计算软件的电机起动仿真计算[J]. 上海电力学院学报, 2013, 29(3): 221-224.
-
[6]靳希, 沙旦华, 张立峰, 等. 大容量电动机启动对孤立小电网的影响[J]. 上海电力学院学报, 2011, 27(6): 579-582.
-
[7]王立德. 电力系统综合负荷模型结构研究[D]. 长沙: 湖南大学, 2008.
-
[8]KUNDUR P. Power systems ability and control[M]. 北京: 中国电力出版社, 2001: 279-305.
-
[9]JUAN A M, JACINTO M A. Voltage sag studies in distribution networks-part Ⅱ: voltage sag assessment[J]. IEEE Trans on Power Delivery, 2006, 21(3): 1679-1688.