|
|
|
发布时间: 2021-02-25 |
计算机与信息科学 |
|
|
|
收稿日期: 2020-06-16
基金项目: 国家自然科学基金(61502297)
中图法分类号: TP242
文献标识码: A
文章编号: 2096-8299(2021)01-0061-06
|
摘要
以实现全向移动平台的位姿控制为主要研究目的。在位姿获取上,采用光流传感器和惯性导航获得了位姿信息;在结构和控制上,研究了四轮麦克纳姆轮的全向移动平台结构及其位姿解算,分析了获得车辆转角和位姿双闭环PID控制规律。通过Simulink仿真建立上位机实时获取传感器数据,研究了各个传感器在不同条件下的数据变化情况和双闭环控制的参数调节问题,以寻找最佳的控制参数。
关键词
双闭环控制; 光流传感器; 惯性导航; 全向移动
Abstract
The main purpose is to realize the pose control of omni-directional mobile platform.In the aspect of pose acquisition, the method of acquiring pose information is provided by using optical flow sensor and inertial navigation.In terms of structure and control, the structure of omni-directional mobile platform of four-wheel mcnamm wheel is studied, the position and attitude calculation is explored, and the double closed-loop PID control law of vehicle angle and position and attitude is analyzed.The upper computer is established by Simulink simulation to obtain the sensor data in real time, so as to study the data change of each sensor under different conditions and the parameter adjustment of double closed-loop control, and find the best control parameters.
Key words
double closed-loop control; optical flow sensor; inertial navigation; omnidirectional movement
随着计算技术和微处理器等技术的发展, 智能化技术发展越来越迅速, 智能机器人的应用也越来越广泛。机器人的巡检运动和定位方式作为机器人的主要功能成为研究机器人学应用的热门方向。因此, 如何运用相应的控制技术、传感器融合技术和视觉技术等成为研究轮式巡检机器人发展的主要课题之一。
目前相关人员在轮式移动发展[1]和传统视觉目标跟踪算法的基础上[2], 针对视觉追踪等问题提出了新的算法, 以便克服干扰; 同时也有在传感器中使用数据融合技术[3], 精准获得信息采集, 再通过相关控制算法, 结合信息融合技术, 以确定障碍物的种类。
本文研究的主要目标是实现全向移动机器人的位姿确定和移动控制。在数据获取方面, 利用光流传感器、惯性导航, 通过各个传感器读取与处理信息; 在结构分析上, 对麦克纳姆轮的结构和移动特点进行了分析和建模, 搭建了实物模型, 并运用相应的传感器技术, 获得了传感器相应技术、单片机和全向机器人结合的现实成果; 在控制上, 以各个传感器获得的数据为基础, 获得了移动平台所需的所有位姿信息, 再利用双闭环控制来实现移动平台的相应位姿变化控制, 并通过实验调整控制参数, 以适应最佳的控制要求。
1 基于光流传感器的位置数据获取
本文使用的光流传感器为是ADNS-3080光流传感器, 能够感应速度高达101.6 cm/s和高速移动的加速度达15 m/s2。通过光学的技术获取连续的表面图像(帧)并在数学上确定移动的方向和大小, 不需要精确的光学对准。
在光流算法中, 一般以两个基本条件为假设前提: 一是亮度恒定, 随着时间变化, 邻近帧间同点的光亮度不改变; 二是小运动, 邻近帧间物体的运动持续, 变化非常小。
在光流算法中, 以上两个条件是光流法使用过程中都要遵循的假设条件, 在现实实验中, 需要基本符合这两个条件。本文采用Lucas-Kanade(LK)光流算法[4]获取瞬时速度数据。
基本的约束条件列写方程为
| $ I(x,y,t) = I(x + {\rm{d}}x,y + {\rm{d}}y,t + {\rm{d}}t) $ | (1) |
式中: I(x, y, z)——第一帧的光强度。
在假定运动了(dx, dy)的间距到下一帧的前提下, 应用了dt的时间, 又假定同一个像素前后光照度一致, 因此式(1)等价条件成立。
将式(1)右端开展泰勒展开可得
| $ \begin{array}{*{20}{l}} {I(x,y,z) = I(x,y,z) + \frac{{\partial I}}{{\partial x}}{\rm{d}}x + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial I}}{{\partial y}}{\rm{d}}y + \frac{{\partial I}}{{\partial t}}{\rm{d}}t + \varepsilon } \end{array} $ | (2) |
式(2)化简后同除以dt获得式(3)
| $ \frac{{\partial I}}{{\partial x}}\frac{{{\rm{d}}x}}{{{\rm{d}}t}} + \frac{{\partial I}}{{\partial y}}\frac{{{\rm{d}}y}}{{{\rm{d}}t}} + \frac{{\partial I}}{{\partial t}} = 0 $ | (3) |
利用u和v分别设定x轴和y轴的速度矢量
| $ \mathit{\boldsymbol{u}} = \frac{{{\rm{d}}x}}{{{\rm{d}}t}},\mathit{\boldsymbol{v}} = \frac{{{\rm{d}}y}}{{{\rm{d}}t}} $ | (4) |
分别用Ix, Iy, It表示图像中像素点灰度沿x, y, t方向的偏导数
| $ {I_x} = \frac{{\partial I}}{{\partial x}},{I_y} = \frac{{\partial I}}{{\partial y}},{I_t} = \frac{{\partial I}}{{\partial t}} $ | (5) |
综上可以得出式(6), 即
| $ {I_x}\mathit{\boldsymbol{u}} + {I_y}\mathit{\boldsymbol{v}} + {I_t} = 0 $ | (6) |
在实际使用中, 均需要从图像数据中获得u和v, 但在当前约束等式下, 没办法解出u和v的准确值。这时要引进其他约束来开展求解。
而在LK光流算法中, 在两种假设的基础条件下, 又添加了第3个条件——一个帧的图像具备近似同样的运动, 以确保全部像素均有相似的运动。以此假设来解决式(6)无法求解的问题。文献[5]研究了利用3×3的窗口内的9个像素点来建立9个方程, 可以写成如下形式
| $ \left[ {\begin{array}{*{20}{c}} {{I_{x1}}}&{{I_{y1}}}\\ {{I_{x2}}}&{{I_{y2}}}\\ \vdots & \vdots \\ {{I_{x9}}}&{{I_{y9}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{u}}\\ \mathit{\boldsymbol{v}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{I_{t1}}}\\ \begin{array}{c} {I_{t2}}\\ \vdots \end{array}\\ {{I_{t9}}} \end{array}} \right] = 0 $ | (7) |
写成矩阵形式
| $ \mathit{\boldsymbol{A\vec v}} + \mathit{\boldsymbol{I}} = 0 $ | (8) |
应用最小二乘法对式(8)开展综合性求解
| $ \mathit{\boldsymbol{\vec v}} = {({\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}})^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}( - \mathit{\boldsymbol{I}}) $ | (9) |
通过上述累加邻域像素点在3个维度的偏导数并做矩阵运算, 可以有效获得光流矢量数值(u, v)。
2 基于惯性导航的角度数据获取
为了获得全向移动平台的全部姿态信息, 需要额外的传感器来获取移动平台转角信息。
MPU-6050运动处理传感器集成了三轴MEMS陀螺仪和三轴MEMS加速度计, 以及一个内嵌的数字运动处理器DMP。下面将从陀螺仪和加速度计的原理和数据处理算法展开。
2.1 基本原理
2.2 数据处理算法
在应用MPU6050中的MEMS陀螺仪时, 普通情况下欧拉角可以通过MEMS陀螺仪直接来计算加速度, 具体为
| $ {v_{{\rm{角}}}} = {v_{{\rm{输出}}}} \times \frac{{2{\kern 1pt} {\kern 1pt} 000}}{{{2^{16}}}} $ | (10) |
| $ {\emptyset _t} = {\emptyset _{t - 1}} + v \times \Delta T $ | (11) |
式中: v角——实际角速度;
v输出——陀螺仪的输出值;
Øt, Øt-1——当前和上一时刻累计的角度;
ΔT——采样固定周期。
通过式(10)中陀螺仪的输出值v输出获得的实际角速度v角, 再根据式(11)来获得角度。下面将详细描述通过三轴加速度计所获得的数据来解算出欧拉角的一个过程。
首先根据加速度的输出值, 计算得到当前的实际加速度a为
| $ a = {a_{{\rm{输出}}}} \times \frac{{4g}}{{{2^{16}}}} $ | (12) |
在各个方向上获取的数据需满足条件: 模长|a|=g, 与重力加速度大小相等、方向相反。
| $ |a| = g = \sqrt {{x^2} + {y^2} + {z^2}} $ | (13) |
式中: x, y, z——重力三轴的分量。
| $ \emptyset = {\rm{arc}}{\kern 1pt} {\kern 1pt} {\rm{cos}}\frac{{\sqrt {{x^2} + {z^2}} }}{g} $ | (14) |
| $ \epsilon = {\rm{arc}}{\kern 1pt} {\kern 1pt} {\rm{sin}}\frac{{\sqrt {{y^2} + {z^2}} }}{g} $ | (15) |
式中: Ø——翻转角Roll角, 为加速度向量与其在xz平面上投影的夹角;
在通过三轴陀螺仪和三轴加速度计分别获得所需的转角信息后, 就可以应用互补融合算法来获得移动平台所需的精确转角信息以提供控制所用。
3 全向移动平台机械结构分析
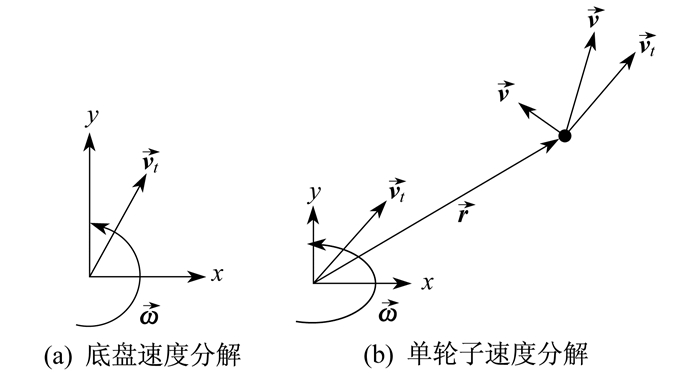
3.1 速度解算
当4个麦克纳姆轮组成底盘时, 计算麦克纳姆轮的速度是实现对各个轮子的调速来控制移动机构整体中心速度的基础。
假设vtx表示x轴速度, 定义向右方向为正; vty表示y轴速度, 定义向前方向为正方向;
图 2为麦克纳姆轮运动速度计算示意。图 2中,
| $ \mathit{\boldsymbol{\vec v}} = {{\mathit{\boldsymbol{\vec v}}}_t} + \mathit{\boldsymbol{\vec \omega }} \times \mathit{\boldsymbol{\vec \gamma }} $ | (16) |
同时再分别计算x轴和y轴的分量[3]
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{v}}_x} = {v_{tx}} - \omega {r_y}}\\ {{\mathit{\boldsymbol{v}}_y} = {v_{ty}} - \omega {r_x}} \end{array}} \right. $ | (17) |
式中: ry, rx——x轴和y轴的间距的一半。
同理可以用式(17)来分别计算另外3个轮子轴心位置速度。根据上述计算结果, 需要计算每个轮子的辊子的速度分别是沿辊子方向的速度
| $ \overrightarrow {{\mathit{\boldsymbol{v}}_ = }} \mathit{\boldsymbol{ = \vec v}} \times \mathit{\boldsymbol{\hat u}} = - \frac{1}{{\sqrt 2 }}{\mathit{\boldsymbol{v}}_x} + \frac{1}{{\sqrt 2 }}{\mathit{\boldsymbol{v}}_y} $ | (18) |
再通过式(18)计算最终需要的轮子的转速[3]
| $ \begin{array}{*{20}{l}} {{v_\omega } = \frac{\mathit{\boldsymbol{v}}}{{\cos {{45}^\circ }}} = \sqrt 2 \left( { - \frac{1}{{\sqrt 2 }}{\mathit{\boldsymbol{v}}_x} + \frac{1}{{\sqrt 2 }}{\mathit{\boldsymbol{v}}_y}} \right) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {\mathit{\boldsymbol{v}}_x} + {\mathit{\boldsymbol{v}}_y}} \end{array} $ | (19) |
将式(17)代入式(19)进行等式整理, 获得单个轮子的最终转速信息[3]为
| $ \left\{ \begin{array}{l} {v_{\omega 1}} = {v_{ty}} - {v_{tx}} + \omega ({r_y} + {r_x})\\ {v_{\omega 2}} = {v_{ty}} + {v_{tx}} - \omega ({r_y} + {r_x})\\ {v_{\omega 3}} = {v_{ty}} - {v_{tx}} - \omega ({r_y} + {r_x})\\ {v_{\omega 4}} = {v_{ty}} + {v_{tx}} + \omega ({r_y} + {r_x}) \end{array} \right. $ | (20) |
式(20)为O-长方形麦轮底盘的逆运动学模型方程[7-10]。综合上述等式, 根据底盘的3个状态信息来解算出4个轮子各自的转速信息。
4 仿真和实验
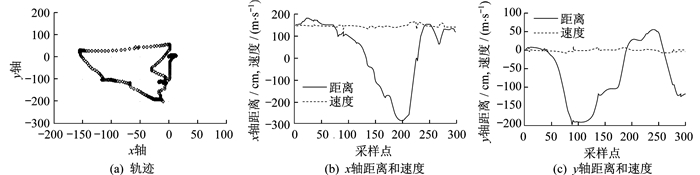
本文采用ADNS3080光流传感器布置于平台底部中心, 与地面距离0.12 m。为充分保证周围的环境光照强度, 在移动平台底部的ADNS3080周围布置2个5 W的LED灯, 同时设置纹理分明且较为平坦的桌面作为采样面。
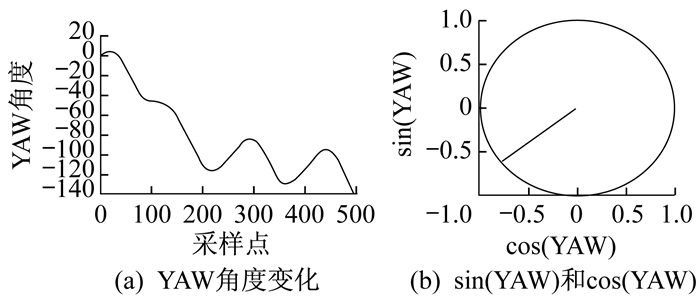
首先对x轴和y轴速度和距离进行单独正向采样测试, 采样点数量大致在200, 得出的数据曲线如图 3所示。同时对一段轨迹进行测试, 得出的数据曲线如图 4所示。用以上同样的方式来测试YAW偏航角, 测试结果如图 5所示。
单环控制PID算法[6]为
| $ \begin{array}{l} {P_{{\rm{pwm}}}} = {K_{\rm{p}}} \times e(k) + {K_{\rm{i}}} \times \sum {e(k)} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {K_{\rm{d}}} \times [e(k) - e(k - 1)] \end{array} $ | (21) |
式中: e(k)——当前计算偏差值;
e(k-1)——前一次计算偏差值。
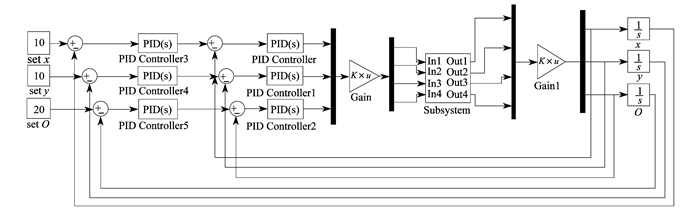
在此次双闭环控制的参数调节中, 调节两环的参数以先内环后外环为准则。此次控制实验主要通过Simulink仿真的形式来进行, 以模拟速度解算环节和双闭环控制环节。其仿真示意如图 6所示。
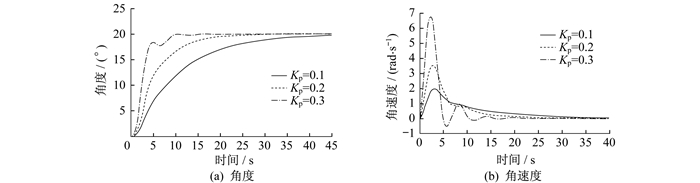
本研究中, 单独对YAW的控制进行参数整定, 设定移动平台的位置目标值为20。在对双闭环进行参数整定时, 首先对外环的位置环进行参数整定。将外环控制器调整保持比例调节系数Kp=1, 再对内环的控制参数进行整定。在位置环的调节中, 对Kp进行单独调节, 分别选择不同的Kp来观测YAW的角度和角速度的变化情况, 结果如图 7所示。
由图 7可知, 随着内环比例调节系数Kp的增加, 系统的调节时间和上升时间都有非常显著的提升, 在选择内环比例环节调节系数Kp=0.3时, 可以在不产生超调量的同时又保持较好的响应速度。
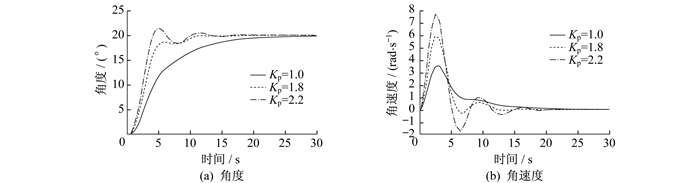
在单独测试完内环的调节后, 将较为适合的比例调节系数Kp=0.3作为外环控制器的固定值。以此为基础进行外环的测试, 速度环也将从纯比例环节开始进行。不同外环比例调节系数Kp下的角度和角速度变化情况如图 8所示。
由图 8可知, 外环的纯比例调节系数Kp的改变能够非常明显地改变底盘角度的输出特性。当比例调节系数Kp从1到2.2变化时, YAW的响应速度有着非常明显的提升, 但达到目标速度后存在稳态误差。因此, 本试验中内环控制还需要引入积分环节用以消除稳态误差。
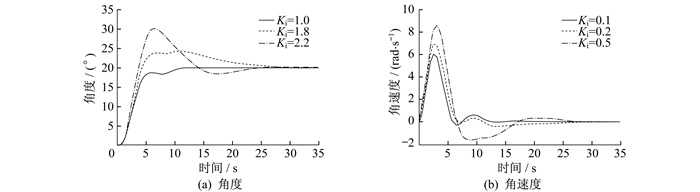
首先固定比例环节Kp=1.8, 再加入积分环节, 通过调节后, 选择积分调节系数Ki=0.1, 其响应曲线如图 9所示。由图 9可知, 加入积分环节后能够非常有效地消除稳态误差, 提高系统整体的稳定性, 并在运行过程中能够非常有效地将YAW稳定至20, 且保持良好。
5 结论
本文基于多传感器数据获取和双闭环控制, 通过对移动平台的速度解算获得底盘与四轮子转速之间的转换关系, 然后利用获得的全向移动平台姿态信息, 通过双闭环串级控制来进行姿态控制。在研究的整个过程中, 得出以下结论:
(1) 通过光流传感器来获得所需要的x轴和y轴距离数据, 在使用LED灯提供持续光照条件下移动10 cm存在1~2 mm的误差, 因此短距离移动对实验的影响非常小;
(2) 本次实验中, 底盘的各个坐标轴方向上的速度能通过运动学的方法解算到每一个轮子上, 麦克纳姆轮存在的结构优势也是全向移动实现的基础;
(3) 双闭环控制能够在系统中同时控制两个关联的状态, 可以通过内外环参数的调整来改善系统整体的性能, 同时扰动和误差也能得到非常好的解决。
参考文献
-
[1]徐冰, 郎旬旬. 轮式移动底盘发展现状分析[J]. 现代制造技术与装备, 2018(7): 90. DOI:10.3969/j.issn.1673-5587.2018.07.041
-
[2]邱雪娜. 基于视觉的运动目标跟踪算法及其在移动机器人中的应用[D]. 上海: 华东理工大学, 2011.
-
[3]吴慧玲. 基于多传感器的移动机器人避障策略的研究[D]. 沈阳: 沈阳大学, 2013.
-
[4]唐舒放, 王志胜, 张舵. 基于光流定位的四旋翼飞行器技术研究[J]. 机械与电子, 2019, 37(7): 54-57.
-
[5]王琳玮, 邵星灵, 杨卫. 基于惯性传感器的球形机器人位姿控制系统及实验研究[J]. 中国测试, 2020, 46(3): 123-127.
-
[6]周航, 朱翰宸, 李园园, 等. 基于麦克纳姆轮的摆式悬挂系统设计及其运动学分析[J]. 电子制作, 2020(9): 65-66.
-
[7]夏杰, 熊俊俏. 基于光流传感器的微型四轴悬停校正系统设计[J]. 现代电子技术, 2019, 42(22): 117-120.
-
[8]宗光华. 机器人的创意设计与实践[M]. 北京: 北京航空航天大学出版社, 2004: 25-35, 138-150.
-
[9]敬如雪, 高玉琢. 基于多传感器的数据融合算法研究[J]. 现代电子技术, 2020, 43(10): 10-13.
-
[10]房兴博, 陶庭叶, 李金超, 等. 基于手机惯性传感器的航向估计算法研究[J]. 传感器与微系统, 2020, 39(5): 17-20.