|
|
|
发布时间: 2021-04-25 |
清洁安全发电 |
|
|
|
收稿日期: 2020-10-26
中图法分类号: TK228
文献标识码: A
文章编号: 2096-8299(2021)02-0121-06
|
摘要
为提高电厂引风机故障预警的准确性,提出了一种基于多元状态估计技术(MSET)和偏离度函数法的引风机故障预警方法。通过引风机正常运行状态下的多变量数据,建立了MSET模型,得到了模型运算的最优估计值。利用偏离度函数判断出实际值与最优估计值之间的偏离度,较直观地反映出故障发展过程。应用该方法对华能浙江某热电厂引风机的故障问题进行了验证,结果表明,该方法能够及时发现引风机的异常,实现引风机的故障预警。
关键词
电厂引风机; 多元状态估计技术; 偏离度函数法; 滑动窗口法; 故障预警
Abstract
In order to improve the accuracy of the fault warning of the induced draft fan in the power plant, a method based on multivariate state estimation technology (MSET) and deviation degree function for the early warning of induced draft fan failure is proposed.The MSET model is established based on the multivariate data under the normal operation of the induced draft fan, and the optimal estimated value calculated by the model is obtained.The deviation degree between the actual value and the optimal estimated value is judged by the deviation degree function, which can intuitively reflect the failure development process.The sliding window method is used to determine the fault warning threshold.Once the deviation exceeds this threshold, an alarm will be issued to inform the staff to solve the problem.The fault problem of the induced draft fan of a thermal power plant in Huaneng Zhejiang is proven with this method.The research results show that this method can detect the abnormality of the induced draft fan in time and realize the early warning of the induced draft fan failure.
Key words
plant induced draft fan; multivariate state estimation technology; deviation degree function; sliding window method; fault early warning
在电厂生产运行过程中, 风机是不可或缺的辅机设备。风机在复杂多变的环境下运行, 会出现多种故障类型, 倘若发生故障就需要停机维修, 则会降低了电厂的经济效益。因此, 需要对电厂风机设备进行监测, 根据现场数据偏离正常值的程度, 对风机采取不同的措施, 避免发生故障需要停机的现象, 尽可能减小电厂的经济损失。传统的监测技术早期主动识别故障的能力非常有限。国内外对风机故障的判断通常是以振动信号为主要依据, 其他信号只起到辅助判断的作用[1]。引风机监测的参数包含振动幅值、温度和压力等, 各参数之间相互关联, 在不同的工况下所表现出的状态也不同, 因此依靠单变量的阈值监测造成故障预警准确率不高。
为了能够提前发现故障和避免漏报, 提高预警准确率, 应进行多变量相关分析。多元状态估计技术(Multivariate State Estimation Technology, MSET)可以为此问题提供一种解决方法。本文根据引风机正常的历史数据, 对其进行MSET建模, 构成状态矩阵, 由状态矩阵产生估计值与实际值相比较而产生正负偏差阈值, 一旦超过报警带, 就可以形成早期异常报警。MSET相比其他方法具有建模简单、满足现场的实时工况等优点。
1 MSET原理
MSET是一种非线性的多变量预测估计算法。通过对设备正常工况下的数据建立模型[2], 根据模型对正常的历史数据做运算, 得出各项参数的最优估计值, 最终对设备的实时数据与最优估计值作对比分析, 根据两者的偏差, 做出诊断结果。
假设设备的测点参数变量有n个, 在某个时刻tj记录的n个参数状态记为观测向量, 即
| $ \begin{array}{c} \mathit{\boldsymbol{X}}\left( {{t_j}} \right) = \left[ {{x_1}\left( {{t_j}} \right)\quad {x_2}\left( {{t_j}} \right)\quad {x_3}\left( {{t_j}} \right)} \right.\\ {\left. { \cdots \quad {x_n}\left( {{t_j}} \right)} \right]^{\rm{T}}} \end{array} $ | (1) |
式中: xi(tj)——tj时刻观测到各个测点的测量值。
在设备正常工况下, 采集到的n个测点参数不同时刻的m个历史测量值, 构成记忆矩阵D, 即
| $ \begin{array}{c} \mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {{x_1}\left( {{t_1}} \right)}&{{x_1}\left( {{t_2}} \right)}&{{x_1}\left( {{t_3}} \right)}& \cdots &{{x_1}\left( {{t_m}} \right)}\\ {{x_2}\left( {{t_1}} \right)}&{{x_2}\left( {{t_2}} \right)}&{{x_2}\left( {{t_3}} \right)}& \cdots &{{x_1}\left( {{t_m}} \right)}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {{x_n}\left( {{t_1}} \right)}&{{x_n}\left( {{t_2}} \right)}&{{x_n}\left( {{t_3}} \right)}& \cdots &{{x_n}\left( {{t_m}} \right)} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{X}}\left( {{t_1}} \right)}&{\mathit{\boldsymbol{X}}\left( {{t_2}} \right)}&{\mathit{\boldsymbol{X}}\left( {{t_3}} \right)}& \cdots &{\mathit{\boldsymbol{X}}\left( {{t_m}} \right)} \end{array}} \right] \end{array} $ | (2) |
MSET建模的基础要先构造出记忆矩阵, 记忆矩阵中每一列观测向量表示的是设备不同时刻的正常工况状态[3]。在记忆矩阵中, 通过对由设备正常工况状态下观测向量组成的子空间分析, 可以展现出设备运行变化的过程。构建记忆矩阵实际上就是对设备运行变化的记忆分析。
将某时刻的设备观测值设为Xobs, 经过MSET模型运算得出的估计值为Xest, Xest是记忆矩阵与权值向量的积[4], 即
| $ \begin{array}{l} \boldsymbol{X}_{\mathrm{est}}=\boldsymbol{D} \cdot \boldsymbol{W}=\\ \left[\begin{array}{llll} \boldsymbol{X}\left(t_{1}\right) & \boldsymbol{X}\left(t_{2}\right) & \boldsymbol{X}\left(t_{3}\right) & \cdots & \boldsymbol{X}\left(t_{m}\right) \end{array}\right] \cdot\\ \left[\begin{array}{lllll} w_{1} & w_{2} & w_{3} & \cdots & w_{m} \end{array}\right]^{\mathrm{T}}=\\ w_{1} \boldsymbol{X}\left(t_{1}\right)+w_{2} \boldsymbol{X}\left(t_{2}\right)+w_{3} \boldsymbol{X}\left(t_{3}\right)+\cdots+\\ w_{m} \boldsymbol{X}\left(t_{m}\right) \end{array} $ | (3) |
权值向量W可以反映记忆矩阵与估计值的相似性程度, 那么权值向量可通过观测值与估计值比较得出的残差计算出来。残差ε可表示为
| $ \boldsymbol{\varepsilon}=\boldsymbol{X}_{\text {est }}-\boldsymbol{X}_{\mathrm{obs}} $ | (4) |
当观测值与估计值越来越接近, 达到理想状态时, 残差ε近乎为零。此刻残差ε的平方和达到最小[5], 残差平方和为
| $ \begin{aligned} S(w)=& \sum\limits_{i=1}^{n} \varepsilon_{i}^{2}=\boldsymbol{\varepsilon}^{\mathrm{T}} \boldsymbol{\varepsilon}=\\ &\left(\boldsymbol{X}_{\mathrm{est}}-\boldsymbol{X}_{\mathrm{obs}}\right)^{\mathrm{T}}\left(\boldsymbol{X}_{\mathrm{est}}-\boldsymbol{X}_{\mathrm{obs}}\right)=\\ &\left(\boldsymbol{D} \cdot \boldsymbol{W}-\boldsymbol{X}_{\mathrm{obs}}\right)^{\mathrm{T}} \cdot\left(\boldsymbol{D} \cdot \boldsymbol{W}-\boldsymbol{X}_{\mathrm{obs}}\right)=\\ & \sum\limits_{i=1}^{n}\left(\sum\limits_{j=1}^{m} w_{j} D_{i j}-\boldsymbol{X}_{\mathrm{obs}}(i)\right)^{2} \end{aligned} $ | (5) |
对S(w)求偏导, 并令其偏导等于零, 即
| $ \begin{array}{l} \frac{\partial S(w)}{\partial w_{k}}= \\ -2 \sum\limits_{i=1}^{n}\left(\sum\limits_{j=1}^{m} w_{j} D_{i j}-\boldsymbol{X}_{\mathrm{obs}}(i)\right) D_{i k}=0 \end{array} $ | (6) |
解得
| $ $ | (7) |
将式(7)整理得
| $ \boldsymbol{W}=\left(\boldsymbol{D}^{\mathrm{T}} \cdot \boldsymbol{D}\right)^{-1} \cdot\left(\boldsymbol{D}^{\mathrm{T}} \cdot \boldsymbol{X}_{\mathrm{obs}}\right) $ | (8) |
为了使该方法能够拥有更加直观的物理意义, 避免DTD表现出不可逆的现象, 将式(8)中点积运算符替换成非线性运算符号⊗, 扩大它的应用领域, 即
| $ \boldsymbol{W}=\left(\boldsymbol{D}^{\mathrm{T}} \otimes \boldsymbol{D}\right)^{-1} \cdot\left(\boldsymbol{D}^{\mathrm{T}} \otimes \boldsymbol{X}_{\mathrm{obs}}\right) $ | (9) |
非线性运算符采用欧氏距离更加能够反映两两向量之间的相似性, 即
| $ (X, Y)=\sqrt{\sum\limits_{i=1}^{n}\left(x_{i}-y_{j}\right)^{2}} $ | (10) |
观测向量与记忆矩阵中向量的相似性由空间距离反映出来。由式(10)可以看出, 它们两向量的相似程度与观测向量所对应的权值成正比。将式(9)代入式(3)可得
| $ \boldsymbol{X}_{\mathrm{est}}=\boldsymbol{D} \cdot\left(\boldsymbol{D}^{\mathrm{T}} \otimes \boldsymbol{D}\right)^{-1} \cdot\left(\boldsymbol{D}^{\mathrm{T}} \otimes \boldsymbol{X}_{\mathrm{obs}}\right) $ | (11) |
在设备正常工作的某一时刻记下n个参数数据当作模型新的观测向量, 构造的记忆矩阵包含了设备的正常工作空间: 当观测向量处于正常工作空间时, 设备处于正常工作状态; 当观测向量超出正常工作空间, 则不能通过MSET模型运算得到估计向量, 模型预测的精度下降, 两向量之间的残差增大[6]。由此可得出, 观测向量与估计向量的残差可以反映出设备是否发生故障。
2 偏离度和预警阈值
根据观测向量与估计向量相比较的差异程度可以反映设备的工作状态, 难点是如何定义差异程度的大小来判断设备的状态和如何合理的设定故障预警阈值[7]。目前, 偏离度函数和滑动窗口法可以很好地处理这两个问题。
2.1 偏离度函数法
权衡两两向量之间的偏离度的方法有很多, 经常采用的是欧氏距离。两个向量之间的偏离度与相似度两者之间的关系成正比, 故观测向量与估计向量的偏离度函数为
| $ S(\boldsymbol{X}, \boldsymbol{Y})=\sqrt{\sum\limits_{i=1}^{n} {w_{i}}^{\prime}\left(x_{i}-y_{j}\right)^{2}} $ | (12) |
式中: X——观测向量;
Y——估计向量;
wi'——观测向量中第i个变量的权重系数。
由于设备的变量数据不同, 则权重的赋值由各变量的故障信息决定。
偏离度与向量X和Y的偏离程度成正比, 偏离度越大, 两者的偏离程度也越大[8]。偏离度变成零的时候, 代表着两个向量无差异, 相似性很高, 设备正常运行。
2.2 滑动窗口法
在某个时间段内, 观测向量与估计向量之间的偏离度序列[9]为
| $ S\left(\boldsymbol{X}_{\mathrm{obs}}, \boldsymbol{X}_{\mathrm{est}}\right)=\left[\begin{array}{lllll}S_{1} & S_{2} & S_{3} & \cdots & S_{N}\end{array}\right] $ | (13) |
在此序列上, 选取宽度为N的滑动窗口, 对窗口内连续N个偏离度求和, 并计算出它们的平均偏离度, 即
| $ \bar{S}=\frac{1}{N} \sum\limits_{i=1}^{N} S_{i} $ | (14) |
根据平均偏离度的值来确定故障预警阈值EAN。设引风机正常工况状态下MSET模型平均偏离度最大值为EN[10], 则故障预警阈值为
| $ E_{\mathrm{A}N}=k E_{N} $ | (15) |
式中: k——故障预警阈值系数, 由设备调试人员根据设备工作经验确定, 一般不小于0.9[11]。
3 基于MSET的引风机故障预警
3.1 引风机建模变量的选取
根据电厂辅机运行规程及电厂风机故障维修单进行分析, 筛选出引风机发生故障时数据变化明显的测点。引风机的测点参数如表 1所示。
表 1
引风机测点参数
| 测点参数 | 测点数量 |
| 引风机X向轴承振动幅值 | 1 |
| 引风机Y向轴承振动幅值 | 1 |
| 引风机前轴温度 | 3 |
| 引风机中轴温度 | 3 |
| 引风机后轴温度 | 3 |
| 电机前轴承温度 | 2 |
| 电机后轴承温度 | 2 |
| 电机定子线圈温度 | 6 |
| 电机电流 | 1 |
| 引风机油箱温度 | 1 |
| 电机功率 | 1 |
电厂安全仪表系统(Safety Instrumentation System, SIS)记录引风机参数的间隔时间是10 min。从SIS系统数据库中提取到引风机轴承振动幅值、电机轴承温度等24个测点参数, 由这些测点参数正常历史数据集去建立预测模型。为了保证模型的准确性, 对电机前后轴承温度各设置2个测点, 引风机前中后轴承温度各设置3个测点, 电机定子线圈温度设置6个测点。
3.2 记忆矩阵的构建
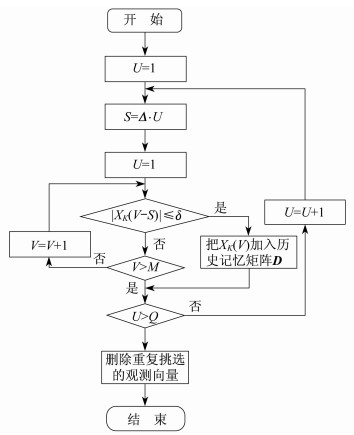
在这24个测点参数的历史数据中要选择出满足引风机所有正常工况下的观测向量, 由模型去分析和学习这些观测向量。对每个测点参数由小到大进行等间距划分, 选择无限接近分割线值的测点参数作为典型观测向量[12]。流程图如图 1所示。
图 1中, U和V为常数, S为分割线值, Δ代表的是步数Q对应的步长, XK(V)为测点参数, δ为趋于零的正数, M代表的是正常工况下的观测向量总数, Q代表的是测点参数XK(V)由小到大等间距划分的步数。
在电厂采集到的这24个测点正常历史数据中去除明显异常的数据, 由剩余数据构成记忆矩阵。由于测点的量级和单位不同, 需将剩余的正常历史数据进行归一化处理, 使输入到模型的数据方便进行计算[13]。公式如下
| $ y=\frac{x-\min (x)}{\max (x)-\min (x)} $ | (16) |
式中: x——采集的测点数据;
y——归一化后的建模数据。
以电机功率归一化后的数据为指标进行等间距抽样, 根据图 1构造记忆矩阵。由此方法构造的记忆矩阵能够基本覆盖设备正常工作状态空间, 降低了矩阵的维数。记忆矩阵构造完成后需将其中的重复观测向量删除, 以保证记忆矩阵中的向量是唯一的[14]。
3.3 仿真的实现
华能浙江某电厂引风机A在2018年9月12日18:30出现故障停机现象, 在发生故障前引风机运行无异常。为了验证本文提出的方法是否可以实现引风机的故障预警, 从电厂的SIS系统中导出2018年8月24日04:00至2018年9月11日22:00期间的2 700组历史正常数据构成记忆矩阵D, 选取2018年9月12日01:50至18:30的100组历史数据组成观测向量集。由MSET模型运算得出估计值, 对观测向量和估计向量两者进行运算, 得到残差和偏离度。各个变量的权重系数在偏离度函数中均取值为1。
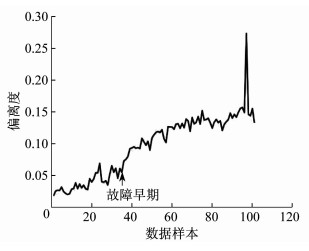
图 2为观测向量集的偏离度曲线。由图 2可知: 从第35组数据开始, 偏离度大体上呈不断上升的趋势; 在第100组数据附近, 偏离度急剧上升, 引风机发生故障停机。
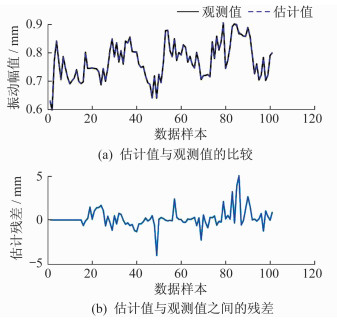
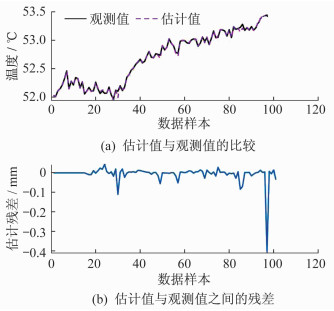
轴承的振动幅值和温度信号是引风机运行过程中的重要参数, 两者也反映了大部分的故障信息[15], 因此本文根据引风机前轴X向轴承振动幅值、前轴Y向轴承振动幅值、前轴承温度、后轴承温度4个变量的观测值与估计值的计算结果, 来检测MSET模型的精度。图 3、图 4、图 5和图 6分别为这4个变量的估计结果和残差。由图 3可知, 引风机前轴X向轴承振动幅值的估计残差小于0.01 mm, 相对残差小于1.4%。由图 4可知, 引风机后轴Y向轴承振动幅值的估计残差小于0.005 mm, 相对残差小于0.7%。由图 5可知, 引风机前轴承温度的估计残差小于0.2 K, 相对残差小于0.3%。由图 6可知, 引风机后轴承温度的估计残差小于0.1 K, 相对残差小于0.2%。由上述计算结果可知, 各变量的估计残差和相对残差均较小, 从而证明MSET模型具有很高的精度。
对比图 3~图 6可知, 引风机前轴X向和Y向轴承振动幅值的估计残差一直在零的附近波动, 变化不大, 但是引风机前轴承和后轴承温度从第90组数据起出现明显增大的现象, 远远大于正常运行状态时的估计残差。根据电厂运行规程可知, 风机的轴承振动幅值包含很多故障信息, 大部分电厂是通过对轴承振动幅值参数的监测来进行诊断和预警; 而此次轴承振动幅值的估计残差变化小, 风机轴承温度的估计残差变化大, 由此可以得出此次事故与轴承振动关联性很小。因此, 通过监测轴承振动幅值的变化来实现故障预警是不可靠的。故障发生后, 经过现场工程师检测发现由于引风机轴承中的润滑油未充满且油脂质量差, 从而引起油脂恶化, 造成轴承温度急剧上升的现象。若引风机继续运行工作, 油脂会变硬、变黑, 造成轴承座内金属摩擦, 时间久了, 会造成轴承损坏, 带来更大的损失。
将偏离度与上述4个变量的估计残差作比较, 偏离度的增长趋势更加明显, 且在故障状态下波动非常大; 而且偏离度动态曲线能更好地发现故障早期的现象, 更早实现故障预警。
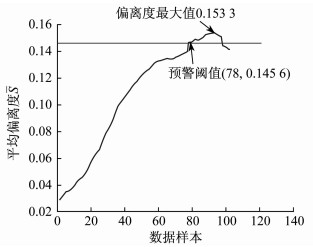
图 7为平均偏离度和预警阈值曲线。选择滑动窗口宽度N为20。由图 7可知, 在引风机发生故障前, 平均偏离度最大值EN=0.153 3, k的取值为0.95, 则故障预警阈值EAN=0.145 6。在第78组(S=0.145 6)和第79组(S=0.146 2)数据之间发出故障预警, 可提前21个数据点发出报警信号, 相当于提前了3.5 h告知现场工作人员引风机运行出现异常现象, 需停机做故障检查。因此, 该方法对风机运行过程中的异常能够提前发现并及时预警。
4 结语
本文利用电厂SIS系统中导出的引风机正常历史数据建立了引风机运行状态监测模型, 即MSET模型。在MSET模型的基础上引入偏离度概念, 再经过滑动窗口法确定预警阈值, 平均偏离度曲线一旦超过之前设定好的预警阈值, 就会提前发出预警信号。在华能浙江某热电厂应用该方法进行验证, 证明MSET模型具有很高的精度且可提前发现设备异常运行状态, 实现早期的故障预警。
参考文献
-
[1]吴新忠, 陈炳光, 牛洪海, 等. 基于EEMD和SVM风机故障诊断的研究[J]. 煤炭技术, 2017, 36(4): 252-254.
-
[2]李俊卿, 王焕仲, 季刚, 等. 基于大数据分析的风机轴承故障预警[J]. 智慧电力, 2020, 48(2): 25-30.
-
[3]韩万里, 茅大钧, 印琪民. 基于PCA和多元状态估计的引风机故障预警[J]. 热能动力工程, 2020, 35(1): 91-97.
-
[4]黄伟, 张泽发. 基于多元状态估计的燃烧室故障预警研究[J]. 汽轮机技术, 2020, 62(1): 38-42.
-
[5]宋莹, 张钟镭. 基于多元状态估计和超椭球分析的汽轮机运行状态监测[J]. 动力工程学报, 2020, 40(2): 138-144.
-
[6]牛玉广, 李晓彬, 张佳辉. 基于多元状态估计与自适应阈值的电站辅机故障预警[J]. 动力工程学报, 2019, 39(9): 717-724.
-
[7]李锋, 潘凤萍, 廖宏楷, 等. 多元状态估计的记忆矩阵选取及风机故障预警方法[J]. 自动化仪表, 2019, 40(1): 74-78.
-
[8]刘耘彰. 电厂风机故障诊断与预警研究[D]. 杭州: 浙江大学, 2019.
-
[9]张令, 刘晖, 李彦文, 等. 火电厂引风机故障预警与诊断综述[J]. 仪器仪表用户, 2019, 26(1): 109-112.
-
[10]王博, 吴智群. 电站风机故障智能预警技术的应用研究[J]. 热能动力工程, 2017, 32(10): 66-70.
-
[11]陈统钱. 基于多元状态估计技术建模的引风机早期诊断研究[J]. 浙江电力, 2017, 36(8): 49-53.
-
[12]王博. 基于多元状态估计的电站风机故障预警方法研究与应用[D]. 西安: 西安热工研究院, 2017.
-
[13]刘涛, 刘吉臻, 吕游, 等. 基于多元状态估计和偏离度的电厂风机故障预警[J]. 动力工程学报, 2016, 36(6): 454-460. DOI:10.3969/j.issn.1674-7607.2016.06.006
-
[14]刘涛. 基于多元状态估计的电站风机故障预警研究及系统开发[D]. 北京: 华北电力大学, 2016.
-
[15]孙小林. 火电厂风机故障预警系统的应用研究[D]. 保定: 华北电力大学, 2015.