|
|
|
发布时间: 2021-06-25 |
智能电网 |
|
|
|
收稿日期: 2020-03-24
基金项目: 上海市科技创新行动计划(19DZ1205402)
中图法分类号: TM723;TM464
文献标识码: A
文章编号: 2096-8299(2021)03-0221-05
|
摘要
为抑制模块化多电平换流器(MMC)内部的环流,提出了一种准比例谐振(PR)控制结合虚拟阻抗的复合环流控制方法。首先分析了MMC的拓扑结构以及内部环流产生的原因;其次设计了PR控制器,对桥臂环流二倍频谐波进行抑制,设计了虚拟阻抗实现对环流高次谐波的抑制;最后在MATLAB/Simulink平台上搭建了五电平MMC逆变电路模型。仿真结果表明,所提出的环流抑制策略能有效减小环流的交流波动幅值。
关键词
模块化多电平换流器; 环流抑制; 准比例谐振控制器; 虚拟阻抗
Abstract
In order to suppress the circulating current inside the modular multilevel converter (MMC), a composite circulating current control method combining quasi-proportional resonance (PR) control and virtual impedance is proposed.The article first analyzes the topological structure of MMC and explains the reasons for the internal circulating current.Secondly, a PR controller is designed to suppress the double-frequency harmonics of the circulating current of the bridge arm, and a virtual impedance is designed to suppress the higher harmonics of the circulating current.Finally, a five-level MMC inverter circuit model was built on the MATLAB/Simulink platform.The simulation results proved that the proposed circulating current suppression strategy can effectively reduce the AC fluctuation amplitude of the circulating current.
Key words
modular multilevel converter; circulating current suppression; quasi-proportional resonance controller; virtual impedance
模块化多电平变流器(Modular Multilevel Converters, MMC)自2002年被提出以来就受到了众多学者的关注。由于其具有功率损耗低、可拓展性强和易于组装等优点[1-2], MMC已被众多国家和厂家广泛应用于高压直流输电、静止同步补偿等电网输送领域。然而, MMC也有着该电路拓扑独有的问题, 如子模块电容电压失衡、内部环流等现象, 其中, 环流抑制是MMC控制系统中极其重要的组成部分[3-5]。
相间环流过大会增加桥臂应力, 增加器件尺寸, 增大功率损耗, 因此必须对环流加以抑制。文献[6]提出了一种通过计算并增大桥臂电感值结合电流控制的方法, 以实现对环流的抑制, 但增大桥臂电感值则会使MMC装置体积增大, 系统能量损耗过高。文献[7]提出了一种通用的环流抑制方法, 不需要常规环流抑制策略中的坐标变换以及控制量的解耦, 适用范围广, 但该策略需要通过计算得出精确的环流电压值, 不易实现。文献[8]提出了一种基于正、负序双坐标系下比例-积分(PI)和重复控制复合控制的环流抑制方法, 适用于三相平衡和三相不平衡系统, 但该方法使用了PI调节器和重复控制器, 需要大量计算, 且参数整定困难。文献[9]设计了一种基于直接反馈控制的桥臂环流抑制方法, 通过谐波分离器将环流中的三次谐波分离出来, 然后通过准比例谐振(Proportional Rresonance, PR)控制器的调节, 产生调制信号的补偿量, 以此抑制二倍频环流, 然而环流中还有其他频次谐波未得到抑制。
针对当前环流抑制方法的不足, 本文根据MMC典型拓扑, 分析了环流产生的机理, 提出了准PR控制器结合虚拟阻抗的复合MMC环流控制策略。在利用准PR控制器对环流二倍频抑制的基础上, 为增强环流抑制效果, 设计了虚拟阻抗对环流的高次谐波成分进行抑制, 最后通过搭建的MMC环流仿真模型对本文所设计的控制器进行了仿真实验验证。
1 MMC基本原理及数学模型
图 1为MMC电路拓扑结构和MMC子模块结构。图 1(a)中, MMC拓扑中每相包含上下两个完全一样的桥臂, 且各桥臂都有n个相同的子模块(SM)、1个电抗器(Lm)和1个等效桥臂电阻(Rm), 交流输入/输出端口则是从上、下桥臂连接点接入。
常见的MMC半桥型子模块通常由1个带续流二极管的全控型开关管组成的半桥结构和1个直流电容C组成, 如图 1(b)所示。其中, ukj和ikj表示j相第k个子模块的电压和电流。通过控制脉冲实现对功率管的关断与导通控制, 可使子模块投入或切除, 使得MMC子模块输出端电压为电容电压uc或者为零。通过控制MMC各相桥臂子模块的开关组合, 可输出想要的N电平电压。
根据MMC的电路拓扑结构, 由基尔霍夫电压定律得
| $ \begin{array}{c} U_{\mathrm{p} j}+U_{\mathrm{n} j}+L_{\mathrm{m}} \frac{\mathrm{d}\left(i_{\mathrm{p} j}+i_{\mathrm{n} j}\right)}{\mathrm{d} t}+ \\ R_{\mathrm{m}}\left(i_{\mathrm{p} j}+i_{\mathrm{n} j}\right)=U_{\mathrm{dc}} \end{array} $ | (1) |
式中: Upj, Unj——j相上、下桥臂等效输出电压, j=a, b, c;
ipj, inj——j相上、下桥臂电流。
各相上、下桥臂电流为
| $ \left\{\begin{array}{l} i_{\mathrm{p} j}=i_{\mathrm{diff} j}+\frac{i_{\mathrm{s} j}}{2} \\ i_{\mathrm{n} j}=i_{\mathrm{diff} j}-\frac{i_{\mathrm{s} j}}{2} \end{array}\right. $ | (2) |
式中: idiffj——j相间环流;
isj——输出交流电流。
由式(2)可以推导出j相间环流表达式为
| $ i_{\mathrm{diff} j}=\frac{i_{\mathrm{p}j}+i_{\mathrm{n} j}}{2} $ | (3) |
2 环流抑制
2.1 环流机理分析
MMC内部环流的产生, 究其根本, 是由各相子模块电容电压不均衡造成的。MMC理想工作模式下, 各个子模块的电容电压时刻保持平衡, 为Udc/N。然而在实际工况下, 由于每一个子模块中电容的一些参数不能实现完全一致, 各开关管导通时间有微小差异等情况, 导致投入的子模块充放电时间存在微小的偏差, 因此各子模块的电容电压值会产生偏差, 不能保持平衡。现有很多文献从变换器能量均衡、桥臂能量守恒以及平均开关函数的角度证明了MMC桥臂相单元环流只包含偶数次谐波, 其中二倍基波频率谐波含量最大, 并且呈显出负序的特点。环流表达式可写为
| $ \begin{array}{c} \lambda_{\mathrm{diff} j}=I_{\mathrm{diffz}j}+I_{2 \mathrm{diff}j} \cos (2 \omega t+\varphi)+ \\ I_{4 \mathrm{diff}j} \cos (4 \omega t+\varphi)+\cdots \end{array} $ | (4) |
其中: Idiffzj——j相环流直流分量;
I2diffj, I4diffj——j相环流二、四倍频分量幅值;
φ——环流相角。
环流的直流分量是维持子模块与外部能量交换而必须存在的, 由输出功率决定其大小。环流的交流偶次谐波分量增大了环流幅值, 提高了器件裕量, 产生了额外的损耗, 因此这部分环流需要通过控制方法消除。
2.2 环流抑制方法
2.2.1 基于准PR控制器的环流抑制策略
PR控制器控制原理是通过产生一个给定信号的极点, 从而使控制器对该频率的交流输入信号的增益非常大, 进而实现对此交流信号的控制。与PID控制器不同的是, PR控制器能够对输入交流信号进行无静差跟踪控制, 且准PR控制器具有抗电网电压频率扰动的优点。准PR控制器的传递函数为
| $ G_{\mathrm{PR}}(s)=k_{\mathrm{p}}+\frac{2 k_{\mathrm{r}} \omega_{\mathrm{c}} s}{s^{2}+2 \omega_{\mathrm{c}} s+\omega_{0}{}^{2}} $ | (5) |
式中: kp, kr——比例控制增益和谐振控制增益;
ωc, ω0——截止频率和谐振频率。
将s=jω代入式(5), 可得
| $ \begin{array}{c} G_{\mathrm{PR}}(\mathrm{j} \omega)=k_{\mathrm{p}}+\frac{\mathrm{j} 2\;k_{\mathrm{r}} \omega_{\mathrm{c}} \omega}{-\omega^{2}+\mathrm{j} 2 \;\omega_{\mathrm{c}} \omega+\omega_{0}{ }^{2}}= \\ \ \ \ \ \ \ \ k_{\mathrm{p}}+\frac{k_{\mathrm{r}}}{1+\mathrm{j} \frac{\omega^{2}-\omega_{0}{ }^{2}}{2\;\omega_{\mathrm{c}} \omega}} \end{array} $ | (6) |
当ω=ω0时, 控制器可实现对输入交流信号频率为ω的分量放大kp+kr倍, 即可实现对该频率分量的无静差追踪控制。其中, 谐振频率ω0是要跟踪控制的信号的频率, 截止频率ωc一般根据电网的扰动情况设置为5 Hz左右。设计PR控制器时, 可通过调节kp和kr的大小, 实现控制器的信号追踪快速性与频率抗干扰性能之间的均衡。
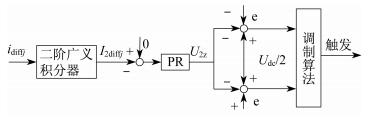
本文采用文献[10]的二阶广义积分器来提取并检测二倍频环流。所提准PR调节器实现对MMC桥臂环流的抑制框图如图 2所示。通过式(3)将得到的桥臂环流送入二阶广义积分器, 得到对应频率的桥臂环流的交流分量。为使环流的交流分量为零, 可将提取出的环流分量与参考值零作比较, 通过准PR调节器调节跟踪, 得到相应桥臂的指令值的补偿量U2z。对于想要消除的环流, 只要并联相应谐振频率的PR调节器即可。
2.2.2 结合虚拟阻抗的环流抑制策略
由于PR控制器只能对特定频次环流进行抑制, 由式(4)可知, 环流中包含除二倍基波频率的波动外, 还含有少量偶数倍基波频率的高次谐波。为了使系统具有较好的环流抑制能力, 则需要多个PR控制器对各偶次环流进行调节, 但由于该方法计算量太大, 不易于控制器实现。因此, 本文采用PR控制器对二倍频环流进行调节抑制, 对于其他频率的桥臂环流谐波, 设计了虚拟阻抗环节实现对环流的抑制。
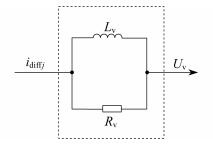
由文献[11]可知, 通过设置MMC系统虚拟阻抗, 可使系统内阻变大, 从而实现对环流的交流分量波动的抑制。但由于添加了虚拟阻抗, 故系统会分出一部分电压用于虚拟阻抗产生的分压, 从而导致系统实际输出交流电压降低。为此, 本文采用如图 3所示的虚拟阻抗对环流中含量较少的高次谐波进行抑制, 使得虚拟阻抗对系统分压较小, 又能使环流得到抑制。图 3中, Lv和Rv为虚拟阻抗, Uv为调制波的修正量。
该虚拟阻抗环节可用一阶惯性环节实现。设惯性环节传递函数为
| $ G(s)=\frac{k T_{\mathrm{s}}}{1+T_{\mathrm{s}}} $ | (7) |
则有
| $ \left\{\begin{array}{l} k=R_{\mathrm{v}} \\ T_{\mathrm{s}}=\frac{L_{\mathrm{v}}}{R_{\mathrm{v}}} \end{array}\right. $ | (8) |
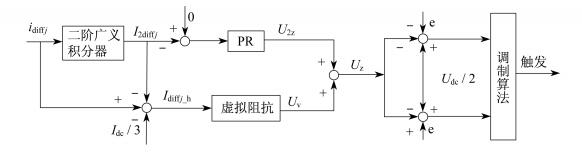
具体设计过程如下: 首先将检测到的环流用二阶广义积分器提取出二倍频分量, 将该分量通过PR调节器调节, 得到调制波修正量U2z; 再将环流中的二倍频和直流分量除去, 此时剩下的环流成分由二次以上的偶次谐波组成, 将该环流通过式(7)的一阶惯性环节, 适当调节虚拟阻抗Rv和Lv的值, 得到调制波的修正量Uv。将两个修正量相加即可得到环流抑制的调制波修正量。PR+虚拟阻抗复合环流抑制策略如图 4所示。
3 仿真验证
为了检验本文所提出的准PR控制结合虚拟阻抗的复合环流抑制策略的有效性, 在MATLAB2018b软件版本的Simulink仿真环境中设计搭建了单相五电平MMC仿真模型, 仿真参数如表 1所示。
表 1
仿真参数
| 参数 | 数值 |
| 直流母线电压/kV | 10 |
| 子模块个数/个 | 4 |
| 子模块电容/mF | 8 |
| 桥臂电抗/mH | 3 |
| 开关频率/kHz | 5 |
| 调制比 | 0.9 |
| 负载/Ω | 5 |
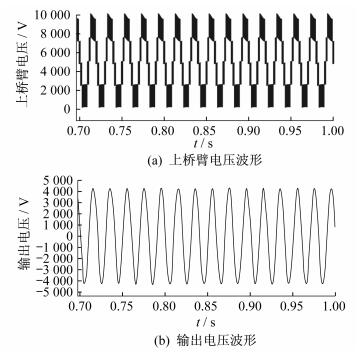
仿真中, MMC系统调制方式为载波移相脉宽调制。图 5(a)和图 5(b)分别显示了采用本文所提环流抑制策略下的系统上桥臂电压波形和输出电压波形。由图 5可以看出: 桥臂输出电平稳定, 说明加入了环流抑制策略后子模块电压能保持均衡; 输出电压波形正弦度良好, 表明加入了本文的环流抑制策略后系统可以正常稳定运行。
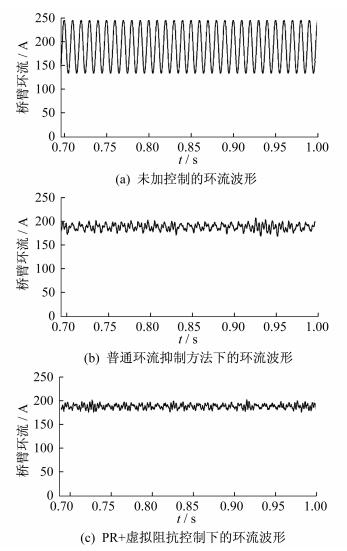
图 6分别显示了采用不同环流抑制策略下的环流波形。由图 6可以看出: 当系统未加入环流抑制策略时, 环流中包含很大幅值的交流成分, 环流的交流分量会增大系统损耗, 这一部分环流需要抑制消除; 当采用广泛使用的准PR控制器环流抑制策略后, 环流的交流分量得到了有效抑制, 交流波动幅值很小, 基本上只含有直流分量; 当采用本文所提环流抑制策略后, 环流相较于单一的PR控制更为平稳, 这是因为设计的虚拟阻抗环节发挥了作用, 抑制了环流中高次谐波的波动, 并使其减小, 所以环流波动幅值更小。
4 结语
本文根据MMC典型电路拓扑, 构建了MMC数学模型, 阐述了桥臂环流发生的原因。为了抑制环流的交流波动, 设计了准PR控制器来抑制环流的二倍频成分, 设计了虚拟阻抗环节抑制环流的高次谐波波动。仿真结果表明, 相较于普通环流抑制方法, PR+虚拟阻抗的复合环流控制策略可以有效抑制环流中的多种频率成分波动, 进一步减小环流波动幅值, 也减小了由于环流问题带来的额外能量损耗。
参考文献
-
[1]刘道远, 程启明, 孙伟莎, 等. 电网电压不平衡条件下MMC控制策略的仿真比较研究[J]. 上海电力学院学报, 2019, 35(6): 553-561.
-
[2]GEMMELL B, DORN J, RETZMANN D, et al. Prospects of multilevel VSC technologies for power transmission[C]//Proceedings of the IEEE/PES Transmission and Distribution Conference and Exposition. Chicago, IL, USA: IEEE, 2008: 1-16.
-
[3]WU D L, PENG L. Analysis and suppressing method for the output voltage harmonics of modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2016, 31(7): 4755-4765.
-
[4]杨晓峰, 林智钦, 郑琼林, 等. 模块组合多电平变换器的研究综述[J]. 中国电机工程学报, 2013, 33(6): 1-14.
-
[5]YANG L M, LI Y H, LI Z X, et al. Loss optimization of MMC by second-order harmonic circulating current injection[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 5739-5753. DOI:10.1109/TPEL.2017.2751068
-
[6]ANTONIO S A, LENNART A, HANS-PETER N. On dynamics and voltage control of the modular multilevel converter[C]//13th European Conference on Power Electronics and Applications (EPE). Barcelona, Spain: IEEE, 2009: 1-10.
-
[7]杨晓峰, 郑琼林. 基于MMC环流模型的通用环流抑制策略[J]. 中国电机工程学报, 2012, 32(18): 59-65.
-
[8]武健, 刘瑜超, 徐修林, 等. 基于双坐标系复合控制的模块化多电平换流器环流抑制方法[J]. 电力系统自动化, 2015, 39(11): 166-172.
-
[9]班明飞, 申科, 王建赜, 等. 基于准比例谐振控制的MMC新型环流抑制器[J]. 电力系统自动化, 2014, 38(11): 85-90.
-
[10]许富强, 周迪青, 付立, 等. 基于二阶广义积分器的谐波电流检测算法[J]. 水电能源科学, 2012, 30(5): 142-144.
-
[11]杨晓峰, 李泽杰, 郑琼林. 基于虚拟阻抗滑模控制的MMC环流抑制策略[J]. 中国电机工程学报, 2018, 38(23): 6893-6904.