|
|
|
发布时间: 2021-06-25 |
图像技术 |
|
|
|
收稿日期: 2020-02-28
基金项目: 国家自然科学基金(61802250)
中图法分类号: TP391
文献标识码: A
文章编号: 2096-8299(2021)03-0295-08
|
摘要
图像哈希是通过将图像提取为简短数列,从而快速地从图库中区分出与原图相似或不同图像的方法。利用奇异值分解(SVD)来分解重构减小图像信息的冗余性和二维变分模态分解(2D-VMD)可以将图像分解成一系列不同中心频率的子模态的特性,从时域和频域提取出图像的主要信息序列来构成哈希。仿真结果表明,相比于其他方法,通过SVD和2D-VMD的紧凑图像哈希算法具有较短的运行时间、较好的鲁棒性和唯一性。
关键词
图像哈希; 奇异值分解; 二维变分模态分解; 子模态
Abstract
Image hashing is a method to quickly distinguish images similar to or different from the original image from a gallery by extracting images into short sequences.Singular value decomposition (SVD) is used to reduce the redundancy of image information and 2D variational mode decomposition (2D-VMD) can decompose the image into a series of sub-modes of different center frequencies, and extract the main information sequence of image from time domain and frequency domain to form hash.The simulation results show that this method has shorter running time, better robustness and uniqueness than other methods.
Key words
image hash; singular value decomposition; 2D-variational mode decomposition; sub-mode
随着数码相机和移动通信的飞速发展, 数字图像广泛应用于各个领域。然而各种简单、易用、快速的图像处理软件的出现使得数字图像很容易被非法使用、篡改和伪造, 从而使数字图像的版权保护渐受关注, 人们需要从大量的多媒体数据中识别出图像的相似版本, 就引出了图像哈希的概念。图像哈希是指使用紧凑序列表示图像及其内容的技术。一般情况下, 图像哈希需要识别出相似图像和不同图像, 即具有鲁棒性和区别性。
1 图像感知哈希算法
图像感知哈希算法的核心是图像特征向量的选取。基于不同的特征提取方法, 研究人员提出了许多不同的算法。目前的图像感知哈希算法大致可分为以下4种。
1.1 基于变换域特征
文献[1]利用离散余弦变换(Discrete Cosine Transformation, DCT)系数来构建图像哈希。该算法将输入图像分割成不重叠的块, 提取每个块第一行/列的DCT系数构建特征矩阵, 最后通过计算和量化列距离进行矩阵压缩。该算法对一些数字运算有较强的鲁棒性, 但对图像的分块导致其对旋转操作不鲁棒。文献[2]提出了一种基于离散傅里叶变换(Discrete Fourier Transform, DFT)的哈希算法。该算法将预处理后的图像通过旋转投影转换为二次图像, 再对二次图像进行DFT变换后提取低频和中频系数作为特征向量来构建哈希。该算法对图像进行了旋转投影, 所以对一般的旋转操作有较强的鲁棒性, 同时在DFT变换后使用非均匀采样提取低中频系数, 从而在概括图像主要信息的同时减少了哈希位数。
文献[3]使用3级小波分解进行哈希构建, 对第2、第3级近似图像应用中心对称局部二值模式得到纹理图像后进行ring分割提取统计特征, 并对第2级分解的高频信息进行位分解统计直方图来得到哈希。该算法使用小波分解可以得到图像多尺度的纹理特征, 但局部二值模式算子受限于采样窗口的大小, 且纹理特征无法表述图像的深层次内容。文献[4]提出了一种基于DCT和离散小波变换(Discrete Wavelet Transform, DWT)的鲁棒图像哈希算法。该算法利用DCT提取稳定的低频系数来构造特征矩阵, 利用DWT将特征矩阵转换为紧凑哈希, 对常规的数字操作较为鲁棒, 但分类性能还需改善。文献[5]将图像的DCT系数进行压缩感知得到的向量作为哈希序列。
1.2 基于数据降维
文献[6]提出了一种基于主成分分析(Principal Component Analysis, PCA)降维的哈希算法。该算法对图像进行分块后按列展开构成二次图像, 然后利用PCA对二次图像进行处理得到降维后的特征, 最后计算特征间距离作为哈希。该算法在拷贝检测应用上的识别率较高, 但因PCA计算复杂度高导致算法效率较低。文献[7]提出了一种基于非负矩阵分解(Non-negative Matrix Factorization, NMF)的图像哈希方法。NMF可以反映出图像的局部特征并滤除掉几何操作的影响, 但对旋转操作不鲁棒。文献[8]考虑到彩色图像各个颜色空间的色调、饱和度等在图像内容表示中起到的作用, 提取HSI和YCbCr颜色空间的块均值和方差来构建哈希。该算法对一般内容保持操作鲁棒, 但同样对旋转比较敏感。文献[9]将图像从RGB空间转化到HSI空间并分块, 提取每个块的颜色特征均值来作为哈希, 但特征提取方法较为单一。
1.3 基于细节特征
文献[10]通过统计图像块中尺度不变特征转换(Scale-Invariant Feature Transform, SIFT)特征点的个数并选取特征点最多的几个图像块来提取颜色、纹理和形状特征。该方法可以有效减少表示图像的特征点个数, 但受限于SIFT特征点的位置和个数的检测不稳定。文献[11]采用多方向多尺度的Gabor滤波器组得到的变换系数作为图像的局部特征, 并加入了哈希码融合来提高算法的查全率, 但同时也影响了算法的效率。文献[12]提出了一种基于颜色矢量角和Canny算子的鲁棒图像哈希算法, 从圆的边缘像素上提取颜色矢量角作为特征, 故有较好的旋转鲁棒性, 但分类性能有待提高。文献[13]利用图像的SIFT特征子来提取和组成特征向量并进行降维, 从而达到对图像的复制、粘贴、篡改的检测。
1.4 其他方法
文献[14]将视觉注意力模型Itti引入到DWT变换的LL子带中, 然后提取不变矩进行哈希构造。该算法具有较强的鲁棒性和区分性。文献[15]结合图像的颜色对立分量和四叉树分解得到的结构特征进行哈希序列的构建。该算法对内容保持操作有较强的鲁棒性。
为了减少原始图像中的数据冗余, 本文首先通过奇异值分解(Singular Value Decomposition, SVD)[16]来分解重构图像的主要信息, 再充分利用二维变分模态分解(2D-Variational Mode Decomposition, 2D-VMD)[17]。其在分解过程中保留各个频率子模态时频信息的特性, 保留包含图像主要内容的模态, 滤除包含大部分噪声的其他模态, 联合保留模态频域系数和时域的统计特征共同构成图像哈希。同时, 为了减少图像哈希序列在传输过程中占用的内存, 本文将图像特征压缩为二值序列。实验结果表明, 本文算法在鲁棒性、区分性以及效率上都优于所比较的算法。
2 本文哈希算法
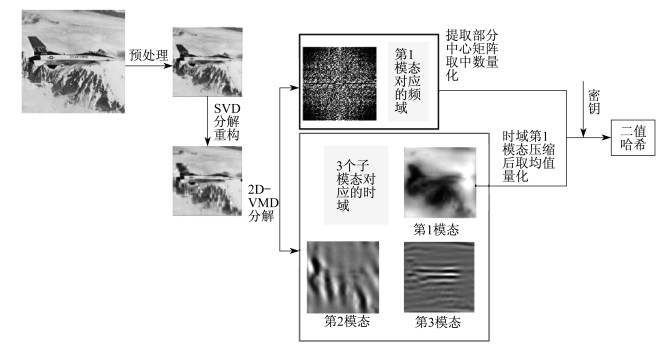
本文哈希算法框图如图 1所示。
算法流程如下: 图像的预处理; 将预处理后的图像进行SVD重构得到二次图像; 对二次图像进行2D-VMD得到3个子模态; 对第1模态时域矩阵各行求均值得到一个列向量, 再对该列向量取均值量化为二值序列; 对第1模态的频域提取中心方形矩阵, 展开为一行, 取中数量化为二值序列; 连接时域特征和频域特征, 并利用密钥对序列进行加密后构成最终的哈希序列。
2.1 图像的预处理
为了增强图像哈希对缩放操作的鲁棒性, 用双线性插值处理将图像规格化为m×m大小, 然后对图像进行高斯低通滤波, 以减小噪声对图像哈希序列的影响。如果输入图像是RGB彩色图像, 则提取其亮度图像。
2.2 图像的分解重构
为了进一步提高哈希算法的鲁棒性, 本文对预处理后的图像进行SVD分解并构建二次图像。
首先, 将预处理后的图像分割成16×16的不重叠的子块, 然后将SVD操作应用于每个子块生成S, V, D 3个矩阵, 其中V为对角矩阵, S和D为正交矩阵, 取矩阵V的前10列与矩阵D的前10行, 矩阵S不变, S×V×D得到重构后的子块, 各重构后的子块按原始顺序排列得到二次图像。具体分解重构过程见文献[11]。
2.3 二维变分模态分解
2D-VMD是一种新型的二维时频信号分析工具, 能够自适应地将图像同时分解为几个不同中心频率的子模态。
2D-VMD函数是VMD函数的二维扩展。其使用拉格朗日乘子法将约束最小化问题转化为无约束问题, 扩展得到的拉格朗日表达式为
| $ \begin{array}{l} L\left(\left\{\boldsymbol{u}_{k}\right\},\left\{\boldsymbol{\omega}_{k}\right\}, \lambda\right)=\sum\limits_{k} \alpha_{k}\left\|\nabla\left[\boldsymbol{u}_{\mathrm{AS}, k} \mathrm{e}^{-\mathrm{j}\left\langle\boldsymbol{\omega}_{k}, x\right\rangle}\right]\right\|_{2}^{2}+ \\ \;\;\;\; \left\|f(x)-\sum\limits_{k} \boldsymbol{u}_{k}(x)\right\|_{2}^{2}+ \\ \;\;\;\; \left\langle\lambda(x), f(x)-\sum\limits_{k} \boldsymbol{u}_{k}(x)\right\rangle \end{array} $ | (1) |
其中:
式中: uk——信号的第k个模态;
ωk——频域的第k个分界面向量;
λ, αk——拉格朗日乘子和混和指数;
uAS, k——频域下的二维解析信号。
通过迭代更新参数
| $\begin{aligned} \boldsymbol{u}_{k}^{n+1}=& \arg \min _{u_{k}}\left\{\alpha_{k}\left\|\nabla\left[\boldsymbol{u}_{\mathrm{AS}, k} \mathrm{e}^{-\mathrm{j}\left\langle\omega_{k}, x\right\rangle}\right]\right\|_{2}^{2}+\right.\\ &\left.\left\|f(x)-\sum\limits_{i} \boldsymbol{u}_{i}(x)+\frac{\lambda(x)}{2}\right\|_{2}^{2}\right\} \end{aligned} $ | (2) |
其中,
利用Parseval傅里叶等距变换, 式(2)可变为
| $ \begin{aligned} \hat{\boldsymbol{u}}_{k}^{n+1}(\boldsymbol{\omega})=&\left(\hat{f}(\mathit{\pmb{Ω}})-\sum\limits_{i \neq k} \hat{\boldsymbol{u}}_{i}(\boldsymbol{\omega})+\frac{\hat{\lambda}(\boldsymbol{\omega})}{2}\right) \cdot \\ & \frac{1}{1+2 \alpha_{k}\left|\boldsymbol{\omega}-\boldsymbol{\omega}_{k}\right|^{2}} \end{aligned} $ | (3) |
其中,
在频域, 式(3)可改写为
| $ \mathit{\boldsymbol{\omega}}_{k}^{n+1}=\frac{\int\limits_ \mathit{Ω} \boldsymbol{\omega}\left|\hat{\boldsymbol{u}}_{k}(\boldsymbol{\omega})\right|^{2} \mathrm{~d} \boldsymbol{\omega}}{\int\limits_ \mathit{Ω} \left|\hat{\boldsymbol{u}}_{k}(\boldsymbol{\omega})\right|^{2} \mathrm{~d} \boldsymbol{\omega}} $ | (4) |
其中,
2D-VMD算法通过在频域内迭代更新3个参数, 得到最优解后进行傅里叶逆变换得到最终结果。算法的具体过程如下:
(1) 初始化
(2) 根据式(3)和式(4), 在频域内更新uk和ωk;
(3) 更新λ, 其中:
2.4 时域特征提取
2D-VMD的第1模态包含了图像的主要信息, 在第1模态提取的时域和频域特征可以很好地代表图像。
第1模态的时域和频域都是一个m×m大小的矩阵。首先对时域矩阵uk各行求均值, 得到一个m×1的列向量u作为时域特征, 接着对u进行二值量化得到一个长度为m的二值哈希序列H1, 量化公式为
| $H_{1}(1, j)=\left\{\begin{array}{l} 1, \text { if } \boldsymbol{u}(i, 1)>\operatorname{mean}(\boldsymbol{u}) \\ 0, \text { else } \end{array}\right. $ | (5) |
式中: H1(1, j)——哈希序列H1的第1行第j列;
u(i, 1)——列向量u的第i行第1列;
mean(u)——对列向量u求均值。
2.5 频域特征提取
第1模态的频域的低频部分分布在频域矩阵
以n为中心, 特征矩阵的范围为
| $ H_{2}(1, j)=\left\{\begin{array}{l} 1, \text { if } \hat{\boldsymbol{u}}(1, i)>\operatorname{median}(\hat{\boldsymbol{u}}) \\ 0, \text { else } \end{array}\right. $ | (6) |
式中: H2(1, j)——哈希序列H2的第1行第j列;
median
2.6 生成哈希
将上述生成的时域二值哈希序列和频域二值哈希序列联合起来得到最终哈希序列, 即
| $H=\left[H_{1}, H_{2}\right] $ | (7) |
式中: H——长度为m+(2d+1)2的二值序列。
利用随机发生器产生m+(2d+1)2个伪随机数序列K作为密钥。通过密钥K对哈希序列进行置乱, 即
| $ h(i)=H(K[i]) $ | (8) |
式中: h——图像最终生成的哈希序列;
i——序列K中第i个数。
2.7 图像相似性度量
对需要检测的图像库和需要查询的图像通过哈希函数得到相应的哈希序列库和查询图像哈希序列, 然后计算查询图像的哈希序列与哈希序列库中的哈希序列的哈希距离。本文利用汉明距离计算哈希距离。当汉明距离小于设定阈值时, 判定图像为相似图像, 否则为不同图像。
汉明距离的计算公式为
| $ d=\sum\left(h_{1}(i) \oplus h_{2}(i)\right) $ | (9) |
式中: d——查询图像哈希序列h1与图像库中任意一幅图像哈希序列h2之间的汉明距离。
3 实验结果
实验参数设置如下: 图像规格化大小m=128, 标准差为3的3×3高斯低通滤波。频域特征矩阵边长的界定值d=9, 因此得到哈希序列的长度为489 bits。
3.1 鲁棒性实验
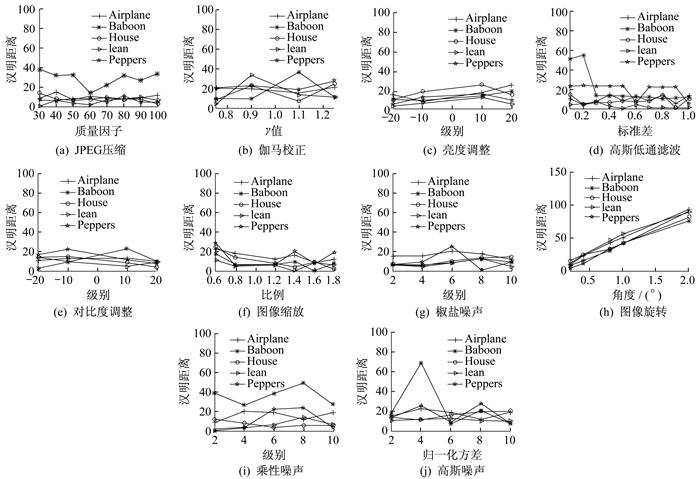
为了评估本文算法的感知鲁棒性, 选用了5幅标准图像, 分别为飞机(Airplane)、狒狒(Baboon)、房屋(House)、莱娜(Lena)、甜椒(Peppers), 如图 2所示。
使用图像处理软件MATLAB和Photoshop以及光影魔术手对每幅原始图像经过JPEG压缩、图像缩放、亮度调整、对比度调整、伽马校正、高斯低通滤波、图像旋转等常规的内容保持操作, 每幅图像生成56个不同的副本, 所以鲁棒性实验图库共有57×5=285幅图像。这些内容保持操作的参数说明和参数设置如表 1所示。
表 1
内容保持操作参数
| 攻击类别 | 软件说明 | 参数说明 | 参数设置 |
| JPEG压缩 | 光影魔术手 | 质量因子 | 30, 40, 50, …, 100 |
| 伽马矫正 | MATLAB | γ值 | 0.75, 0.9, 1.1, 1.25 |
| 亮度调整 | Photoshop | 级别 | -20, -10, 10, 20 |
| 3×3高斯低通滤波 | MATLAB | 标准差 | 0.1, 0.2, 0.3, …, 1 |
| 对比度调整 | Photoshop | 级别 | -20, -10, 10, 20 |
| 图像缩放 | MATLAB | 比例 | 0.6, 0.8, 1.2, 1.4, 1.6, 1.8 |
| 椒盐噪声 | MATLAB | 级别 | 0.002, 0.004, 0.006, 0.008, 0.010 |
| 图像旋转 | MATLAB | 角度 | 0.2, 0.4, 0.8, 1, 2 |
| 乘性噪声 | MATLAB | 级别 | 0.002, 0.004, 0.006, 0.008, 0.010 |
| 高斯噪声 | MATLAB | 归一化方差 | 0.002, 0.004, 0.006, 0.008, 0.010 |
通过本文提出的哈希算法将285幅图像的哈希序列提取出来, 对每幅原始图像的哈希序列和其经过内容保持操作生成的副本的哈希序列计算汉明距离。它们的鲁棒性实验结果如图 3所示。其中所有图形的纵坐标均为各内容保持操作图形与原图的汉明距离, 图形(a)~(j)的横坐标为各攻击操作的参数, 参数类别依次为质量因子、γ值、级别、标准差、级别、比例、级别、角度、级别、归一化方差。
由图 3可以看出, 除了旋转操作随着旋转角度的增加与原图的汉明距离也增大, 其他类型的攻击的距离波动曲线都比较平稳且与原图的汉明距离远小于100。由此表明, 该算法对JPEG压缩、图像缩放、亮度调整、对比度调整、伽马校正、高斯低通滤波和小角度旋转都具有鲁棒性。由于图像经过旋转后像素所在的行会发生变化, 而时域特征直接对矩阵各行取均值量化, 因此该算法对大角度旋转操作不鲁棒。
3.2 区分性实验
以华盛顿大学Ground Truth Database图库中700幅彩色风景图像和数据库VOC2007中300幅彩色目标物体图像共1 000幅图像作为数据集进行区分性实验。1 000幅图像一共有499 500个不同图像对, 对1 000幅图像使用图像处理软件MATLAB和Photoshop以及光影魔术手做相应的内容保持操作, 具体参数如表 2所示, 每幅图像可生成14幅相似图像, 所以1 000幅图像一共有105 000个相似图像对。然后, 使用汉明距离分别计算不同图像对哈希序列之间的距离和相似图像对哈希序列之间的距离作为横坐标, 统计各个距离的数目作为纵坐标。实验结果如图 4所示。
表 2
内容保持操作参数
| 攻击类别 | 软件工具 | 参数说明 | 参数设置 |
| 亮度调整 | Photoshop | 级别 | -20, 20 |
| 对比度调整 | Photoshop | 级别 | -20, 20 |
| 伽马矫正 | MATLAB | γ值 | 0.75, 1.25 |
| JPEG压缩 | 光影魔术手 | 质量因子 | 40, 80 |
| 图像缩放 | MATLAB | 比例 | 0.5, 1.5 |
| 椒盐噪声 | MATLAB | 级别 | 0.002, 0.006 |
| 3×3高斯低通滤波 | MATLAB | 标准差 | 0.2, 0.6 |
由图 4可知, 选择合适的阈值可以近似区分开相似图像和不同图像。这里引入检错率和碰撞率公式[18], 即
| $ \begin{array}{l} P_{\mathrm{E}}=\frac{N_{\mathrm{E}}}{N_{\mathrm{S}}} \end{array} $ | (10) |
| $ \begin{array}{l} P_{\mathrm{C}}=\frac{N_{\mathrm{C}}}{N_{\mathrm{D}}} \end{array} $ | (11) |
式中: PE, PC——检错率和碰撞率;
NE——在一定阈值下, 相似图像对被检测为不同图像对的数目;
NS, ND——相似图像对的总数目和不同图像对的总数目;
NC——不同图像对检测为相似对的数目。
由图 4可以看出, 相似图像对与不同图像对之间的距离有少量交集。取不同阈值得到的检错率和碰撞率如表 3所示。
表 3
不同阈值下的检错率和碰撞率
| 阈值 | PC | PE |
| 66 | 0 | 2.1×10-4 |
| 68 | 4.0×10-6 | 1.2×10-4 |
| 70 | 6.0×10-6 | 6.7×10-5 |
| 73 | 1.8×10-5 | 0 |
由表 3可知, 检错率与碰撞率相互矛盾, 检错率越小, 碰撞率越大, 取阈值为70时, 算法的检错率和碰撞率较低。
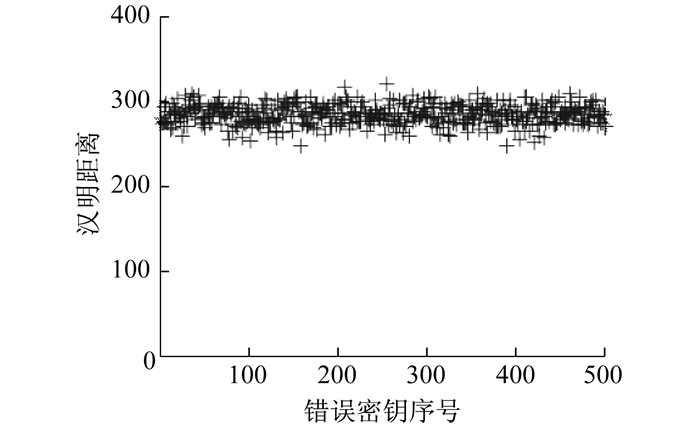
3.3 安全性分析
3.4 参数讨论
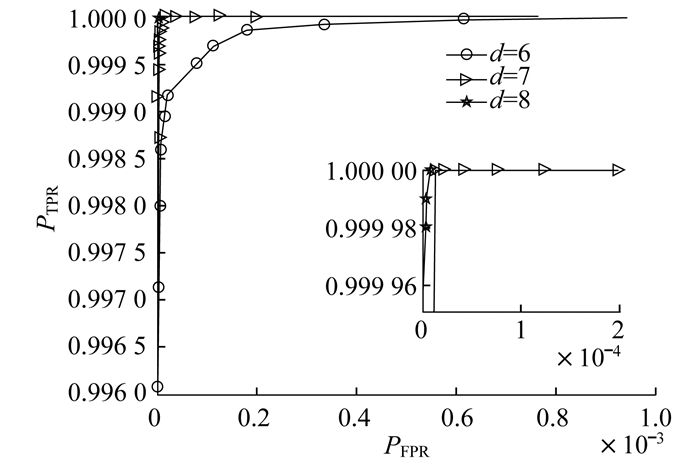
讨论决定频域特征矩阵参数d的大小对算法性能的影响, d分别取6, 7, 8时, 图像的哈希位数分别为297, 353, 417。测试图像依旧使用上文构建的1 000幅彩色图像, 共有499 500个不同图像对和105 000个相似图像对。
本文引入ROC曲线[19]来对比不同参数取值对算法性能的影响。ROC曲线由一系列横坐标为PFPR(False Positive Rate, FPR), 伪阳性率, 表示不同图像被错误判断为相似图像的比率; 纵坐标为PTPR(True Positive Rate, TPR), 真阳性率, 表示相似图像被正确判断为相似图像的比率的点组成。PFPR和PTPR的计算公式为
| $ \begin{array}{l} P_{\mathrm{FPR}}=\frac{N_{\text {false }}}{N_{1}} \end{array} $ | (12) |
| $ \begin{array}{l} P_{\mathrm{FPR}}=\frac{N_{\text {false }}}{N_{1}} \end{array} $ | (13) |
图 6为d不同取值下的ROC曲线对比。
由图 6可以看出, PFPR越小, 哈希算法的区分性越好, PTPR越大, 哈希算法的鲁棒性越好, 所以ROC曲线越靠近坐标轴左上角, 哈希算法的分类性能越好。当d=7和d=8时, 算法的性能十分接近, 但图像哈希序列的位数却增加了64位, 而相较于d=6, d=7时哈希位数虽然增加了56位, 但分类性能提升非常明显。为了使算法能够生成性能良好又紧凑的哈希, 所以d值取7。
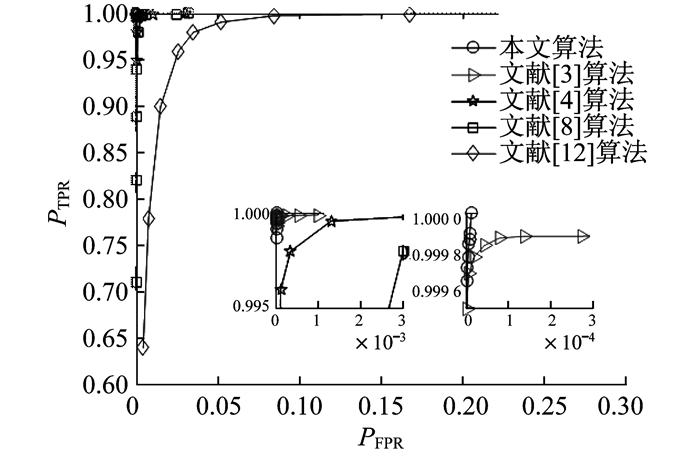
3.5 不同哈希算法性能比较
图 7为本文算法与其他哈希算法的ROC曲线比较。实验依然使用上文构建的1 000幅彩色图像, 共有499 500个不同图像对和105 000个相似图像对。由图 7可以看出, 本文所提出的哈希算法的ROC曲线优于其他算法的ROC曲线, 表明本文所提哈希算法的分类性能优于其他算法。
此外, 还将本文算法与其他算法的运行时间进行了对比。这是通过记录1 000幅图像提取哈希的总耗时然后取均值来实现的。所有算法均采用MATLAB 2016a实现。所使用的计算机配置如下: CPU为Intel Core i5-4590S, 主频为3.00 GHz, RAM容量为4.00 GB。不同算法的运行时间和哈希长度对比如表 4所示。
表 4
不同算法的运行时间和哈希长度
由表 4可以看出, 在处理时间上, 本文所提哈希算法处理一幅图像的平均时间比文献[3]和文献[12]的哈希算法快, 比文献[4]和文献[8]的哈希算法慢, 但分类性能远优于这两种算法。同时, 文献[3]算法、文献[4]算法、文献[8]算法、文献[12]算法以及本文算法最终生成的哈希长度分别为336个整数, 64 bits, 64个整数, 40个整数, 353 bits。其中, 文献[4]算法哈希长度最短, 但分类性能与本文算法相比有明显差距, 而本文算法相较于其他3种哈希序列为整数的算法哈希长度更加紧凑, 占用传输内存更小。
4 结语
本文提出了一种结合SVD和2D-VMD的紧凑图像哈希算法。通过SVD构建二次图像来提取图像的主要内容, 再使用变分模态分解滤除图像中所包含的一些冗余信息及噪声来生成紧凑鲁棒的哈希序列。通过对开放图像数据集的实验结果表明, 与近年来的其他图像哈希算法相比, 本文所提算法具有更好的鲁棒性、区分性和安全性, 且哈希序列更为紧凑。由此验证了本文所提算法的有效性。
参考文献
-
[1]TANG Z J, YANG F, HUANG L Y, et al. Robust image hashing with dominant DCT coefficients[J]. Optik, 2014, 125(18): 5102-5107. DOI:10.1016/j.ijleo.2014.05.015
-
[2]QIN C, CHANG C C, TSOU P L. Robust image hashing using non-uniform sampling in discrete Fourier domain[J]. Digital Signal Processing, 2013, 23(2): 578-585. DOI:10.1016/j.dsp.2012.11.002
-
[3]沈麒, 赵琰. 面向拷贝检测的图像哈希算法[J]. 计算机应用研究, 2019, 36(2): 611-614.
-
[4]TANG Z, YANG F, HUANG L, et al. DCT and DWT based image hashing for copy detection[J]. Icic Express Letters, 2013(7): 2961-2967.
-
[5]刘风林, 刘凯, 张珍珍, 等. 基于DCT系数与压缩感知的图像哈希算法[J]. 软件导刊, 2017, 16(12): 210-212.
-
[6]唐振军, 杨帆, 黄紫晴, 等. 基于PCA特征距离的图像哈希算法[J]. 广西师范大学学报(自然科学版), 2016, 34(4): 9-18.
-
[7]MONGA V, MIHCAK M K. Robust and secure image hashing via non-negative matrix factorizations[J]. IEEE Transactions on Information Forensics and Security, 2007, 2(3): 376-390. DOI:10.1109/TIFS.2007.902670
-
[8]TANG Z, ZHANG X, DAI X, et al. Robust image hash function using local color features[J]. AEU-International Journal of Electronics and Communications, 2013, 67(8): 717-722. DOI:10.1016/j.aeue.2013.02.009
-
[9]赵琰, 周俊杰. 基于颜色特征的图像摘要算法[J]. 上海电力学院学报, 2010, 26(5): 489-492. DOI:10.3969/j.issn.1006-4729.2010.05.019
-
[10]ZHAO Y, ZHAO Q. Robust image hashing based on local features for image authentication[C]//Proceedings of 2nd International Conference on Software, Multimedia and Communication Engineering (SMCE2017). Shanghai, China, 2017: 121-125.
-
[11]李新伟, 夏秀珍. 基于内容结构图的鲁棒图像哈希[J]. 应用科学学报, 2016, 34(6): 691-701. DOI:10.3969/j.issn.0255-8297.2016.06.005
-
[12]TANG Z, HUANG L, ZHANG X, et al. Robust image hashing based on color vector angle and canny operator[J]. AEU -International Journal of Electronics and Communications, 2016, 70(6): 833-841. DOI:10.1016/j.aeue.2016.03.010
-
[13]马伟鹏, 林敏锐, 吴泽宇, 等. 基于SIFT和感知哈希的图像复制粘贴篡改检测方法[J]. 现代计算机, 2019(15): 56-59. DOI:10.3969/j.issn.1007-1423.2019.15.011
-
[14]TANG Z J, ZHANG H Y, PUN C M, et al. Robust image hashing with visual attention model and invariant moments[J]. IET Image Processing, 2020, 14(5): 901-908. DOI:10.1049/iet-ipr.2019.1157
-
[15]SHEN Q, ZHAO Y. Perceptual hashing for color image based on color opponent component and quadtree structure[J]. Signal Processing, 2020, 166: 107244.1-107244.12.
-
[16]QIN C, SUN M H, CHANG C C. Perceptual hashing for color images based on hybrid extraction of structural features[J]. Signal Processing, 2018, 142: 194-205. DOI:10.1016/j.sigpro.2017.07.019
-
[17]DRAGOMIRETSKIY K, ZOSSO D. Two-dimensional variational mode decomposition[C]//Energy Minimization Methods in Computer Vision and Pattern Recognition. Springer, Cham, 2015: 197-208.
-
[18]赵琰, 王朔中, 姚恒, 等. 结合保角变换和Zernike矩的稳健图像Hash[J]. 应用科学学报, 2012, 30(1): 75-81. DOI:10.3969/j.issn.0255-8297.2012.01.012
-
[19]FAWCETT T. An introduction to ROC analysis[J]. Pattern Recognition Letters, 2006, 27(8): 861-874. DOI:10.1016/j.patrec.2005.10.010