|
|
|
发布时间: 2021-08-25 |
清洁安全发电 |
|
|
|
收稿日期: 2020-10-17
基金项目: 上海绿色能源并网工程技术研究中心项目(13DZ2251900)
中图法分类号: TM732
文献标识码: A
文章编号: 2096-8299(2021)04-0335-10
|
摘要
搭建了园区型综合能源系统的基本网架结构,建立了热泵机组、热电联产机组、蓄热罐、电锅炉、电制冷机、余热吸收式制冷机的数学模型,构建了考虑园区供能网约束的双层优化配置模型。模型上层以最小化园区能源站的年综合投资成本为目标,模型下层以系统的年运行费用最低为目标,并基于配电网的Distflow二阶锥模型和线性热网络方程建立供能网络模型。在规划求解过程中,引入了二阶锥松弛技术对模型的电网潮流约束进行凸优化松弛,同时采用了线性热网络方程,以提升模型的可解性和计算速度。最后在改进的IEEE-33节点配电网和8节点供热系统中进行了算例分析,结果表明,所构建的系统优化配置模型在一定程度上提高了园区型综合能源系统的经济性,验证了所提模型的有效性。
关键词
综合能源系统; 双层优化配置; 网络约束; 二阶锥
Abstract
This paper builds the basic grid structure of the park-type integrated energy system, establishes the mathematical models of heat pump units, cogeneration units, heat storage tanks, electric boilers, electric refrigerators, and waste heat absorption refrigerators, and constructs a double-layer optimal configuration model considering the constraints of the park's energy supply network constraint.The upper layer of the model aims to minimize the annual comprehensive investment cost of the energy station in the park, and the lower layer of the model aims at the lowest annual operating cost of the system.Based on the Distflow second-order cone model of the distribution network and linear heat network equation the energy supply network model is established.In the process of planning and solving, the second-order cone relaxation technology is introduced to perform convex optimization relaxation on the power flow constraints of the model.At the same time, linear heat network equations are used to improve the solvability and calculation speed of the model.Finally, an example is analyzed in the modified IEEE-33-node distribution network and 8-node heating network system.The results prove that the system optimization configuration model constructed improves the economy of the park-type integrated energy system to a certain extent, and verifies the effectiveness of the proposed model.
Key words
integrated energy system; double-layer optimal allocation; network constraints; second-order cone
中国存在能源消费结构不均衡、环境污染、产能过剩和使用效率低下等突出问题[1]。综合能源系统(Integrated Energy System, IES)[2]突破了传统电、气、冷、热单一化供能的形式, 实现了多能协同互补和梯级利用的“源-网-荷-储”纵向一体化, 可有效地开发和利用可再生能源, 提高能源的利用率、清洁性[3]。大型园区, 如高校校园、工商业园区、科技产业园区(上海松江G60科技产业园区)等, 具有冷热电气多种能源需求持续增长但能源结构不合理、电力负荷峰谷差较大的特点, 而且园区内终端用能设备灵活多样, 提升能效的潜力巨大。
目前, 国内外学者就园区型综合能源系统优化调度方面的研究主要围绕系统内设备调动的灵活性、可再生能源的消纳以及系统运行的经济性展开。文献[4]讨论的园区综合能源系统包括冷、热、电三联供机组、蓄电池、光伏、电锅炉等设备, 并构建了以系统年运行总成本、年污染物排放量和年能耗量为优化目标的多目标优化调度模型。文献[5]基于不同品位能源的梯级利用, 构建了满足用户冷、热、电、气多元能源需求的工业园区综合能源系统优化调度模型, 并以广州某工业园区的总运行成本最低为目标, 证明了考虑不同品位能源系统梯级利用的调度方法较传统调度方案在系统的日运行成本和能源利用效率上均有较大程度的提升。文献[6]提出了一种“风电机组-热电联产机组-蓄热式电锅炉机组”的区域电-热综合能源系统协同优化运行方法, 以购电成本、燃料成本、弃风惩罚成本之和为总成本, 建立其日前经济调度模型, 提升了热电联产机组的供电和供热空间、促进了系统风电的消纳, 降低了系统的购能成本。文献[7]在分布式风电机组接入的含多能源储能的微能源网中, 加入了电转气(Power to Gas, P2G), 构建了考虑用户侧需求响应的优化调度模型, 以实际算例验证了P2G可以有效地消纳风电、降低系统运行成本。文献[8]在社区型综合能源系统中, 根据冷、热、电、气多元负荷需求特性的不同, 分别构建了各自的需求响应模型, 并以系统的用能成本、柔性负荷补偿成本和碳排放惩罚成本所组成的总成本最低为目标函数, 以具体算例验证了考虑多元负荷需求响应和碳排放对社区综合能源系统经济和环境效益的提升。上述文献主要对综合能源系统的经济性和效率进行了研究, 并未考虑配电网和供冷/热网的网络特性对系统运行成本和系统内设备容量配置的影响。
针对上述问题, 本文提出了一种考虑供能网络约束的园区型电-热综合能源系统能源站双层优化配置模型。上层优化问题以综合能源系统能源站总体投资和运行成本最小为目标, 下层优化问题以一个自然年内的含能源购买成本的运行费用最小为目标, 基于配电网络的二阶锥模型和线性热网方程构建了计及供能网络约束的优化调度模型, 用于模拟既定配置下的系统运行成本。最后通过不同场景对比验证了本模型的合理性和有效性。
1 园区型电热综合能源系统建模
1.1 IES能源站网络架构
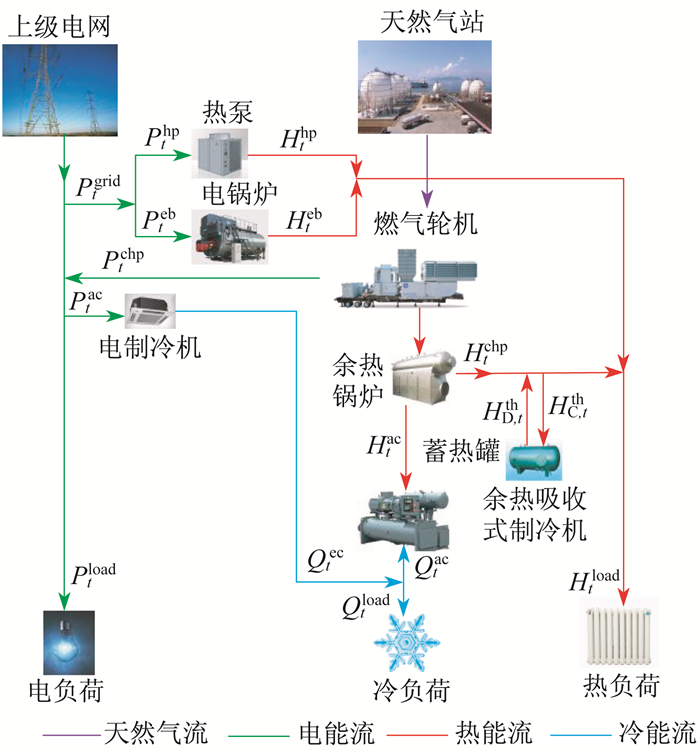
园区型IES能源站的网络架构如图 1所示。综合能源系统在结构上可以看作是具备多输入、多输出、多转换、多元存储等环节的能源单元, 具有较高的可建设性和运行灵活性。本文基于能源集线器模型, 构建了IES能源站的基本模型。其中, 能源输入包含上级电网和天然气站, 能源转换设备包含热泵机组(Heat Pump, HP)、热电联产机组(Combined Heating and Power, CHP)、电锅炉(Electric Boiler, EB)、电制冷机(Electric Cooler, EC)、余热吸收式制冷机(Absorption Chiller, AC), 能源存储为蓄热罐(Thermal Storage, TS), 多元负荷主要有电、热、冷负荷。
1.2 能源转换设备模型
1.2.1 CHP机组模型
CHP机组通过燃烧天然气提供电能和热能, CHP机组通常分背压式和抽汽式[9]两种。为简化分析, 本文仅讨论背压式CHP机组。其模型为
| $ \left\{ \begin{array}{l} P_t^{{\rm{chp}}} = V_t^{{\rm{chp}}}{\phi _{{\rm{ng}}}}\eta _{\rm{e}}^{{\rm{chp}}}\\ H_t^{{\rm{chp}}} = \alpha P_t^{{\rm{chp}}}\\ I_t^{{\rm{chp}}}P_{{\rm{min}}}^{{\rm{chp}}} \le P_t^{{\rm{chp}}} \le I_t^{{\rm{chp}}}P_{\max }^{{\rm{chp}}} \end{array} \right. $ | (1) |
式中: Ptchp, Htchp——CHP机组t时刻发出的电、热功率;
Vtchp——CHP机组t时刻消耗的天然气体积;
ϕng——天然气低热值, 取9.97 kWh/m3;
ηechp, α——CHP机组的发电效率和热电比;
Itchp——t时刻反应CHP机组运行状态的0-1变量, Itchp=1, CHP机组处于运行状态, Itchp=0, CHP机组处于停运状态;
Pminchp, Pmaxchp——CHP机组发出电功率的最小值和最大值。
1.2.2 电锅炉模型
电锅炉模型为
| $ \left\{ \begin{array}{l} H_{_t}^{^{{\rm{eb}}}} = {\eta ^{{\rm{eb}}}}P_{_t}^{^{{\rm{eb}}}}\\ I_{_t}^{^{{\rm{eb}}}}P_{_{{\rm{min}}}}^{^{{\rm{eb}}}} \le P_{_{{t}}}^{^{{\rm{eb}}}} \le I_{_t}^{^{{\rm{eb}}}}P_{_{{\rm{max}}}}^{^{{\rm{eb}}}} \end{array} \right. $ | (2) |
式中: Hteb, Pteb——电锅炉机组在t时刻消耗的热、电功率;
ηeb——电锅炉的产热效率;
Iteb——t时刻表征电锅炉运行状态的0-1变量, Iteb=1, 电锅炉处于运行状态, Iteb=0, 电锅炉处于停运状态;
Pmineb, Pmaxeb——电锅炉电功率的最小值和最大值。
1.2.3 热泵模型
热泵具有较高的能效比, 具有较好的节能效果。
| $ \left\{ \begin{array}{l} H_{_t}^{{\rm{hp}}} = {\rm{COP}}{^{{\rm{hp}}}}P_{_t}^{^{{\rm{hp}}}}\\ I_t^{{\rm{hp}}}P_{_{{\rm{min}}}}^{^{{\rm{hp}}}} \le P_t^{{\rm{hp}}} \le I_t^{{\rm{hp}}}P_{\max }^{{\rm{hp}}} \end{array} \right. $ | (3) |
式中: Hthp, Pthp——热泵机组在t时刻消耗的热、电功率;
COPhp——热泵的电热转换效能系数;
Ithp——t时刻反应热泵运行状态的0-1变量, Ithp=1, 热泵处于运行状态, Ithp=0, 热泵处于停运状态;
Pminhp, Pmaxhp——热泵机组电功率的最小值和最大值。
1.2.4 蓄热罐模型
蓄热罐模型为
| $ \left\{ \begin{array}{l} 0 \le H_{{\rm{C}},t}^{{\rm{th}}} \le I_{{\rm{C,}}\mathit{t}}^{{\rm{th}}}H_{{\rm{C,max}}}^{{\rm{th}}}\\ 0 \le H_{{\rm{D}},t}^{{\rm{th}}} \le I_{{\rm{D,}}\mathit{t}}^{{\rm{th}}} \le 1\\ 0 \le I_{{\rm{C}},t}^{{\rm{th}}} + I_{{\rm{D}},t}^{{\rm{th}}} \le 1\\ W_t^{{\rm{th}}} = W_{t - 1}^{{\rm{th}}} + \left( {\frac{{\eta _{\rm{C}}^{{\rm{th}}}H_{{\rm{C}},t}^{{\rm{th}}} - H_{{\rm{D}},t}^{{\rm{th}}}}}{{\eta _{\rm{D}}^{{\rm{th}}}}}} \right)\Delta T\\ W_{{\rm{min}}}^{^{{\rm{th}}}} \le W_t^{{\rm{th}}} \le W_{\max }^{{\rm{th}}}\\ W_1^{{\rm{th}}} = W_{24}^{{\rm{th}}} \end{array} \right. $ | (4) |
式中: HC, tth, HD, tth——蓄热罐t时刻吸收和释放的热功率;
IC, tth, ID, tth——t时刻反应蓄热罐吸收和释放热量运行状态的0-1变量, IC, tth=1, 余热吸收式制冷机吸收热能, ID, tth=1, 蓄热罐释放热能;
HC,maxth, HD,maxth——蓄热罐吸收和释放热能的最大功率;
Wtth——蓄热罐t时刻储存的热量;
ηCth, ηDth——蓄热罐的吸热和放热效率;
ΔT——调度周期, ΔT=1 h, 一天共有24个调度周期;
Wminth, Wmaxth——蓄热罐存储的最小热量和最大热量。
1.2.5 余热吸收式制冷机模型
余热吸收式制冷机利用余热锅炉的余热进行制冷, 其模型为
| $ \left\{ \begin{array}{l} Q_t^{{\rm{ac}}} = {\rm{CO}}{{\rm{P}}^{{\rm{ac}}}}H_t^{{\rm{ac}}}\\ I_t^{{\rm{ac}}}H_{\min }^{{\rm{ac}}} \le H_{{\rm{C}}, t}^{{\rm{ac}}} \le I_t^{{\rm{ac}}}H_{\max }^{{\rm{ac}}} \end{array} \right. $ | (5) |
式中: Qtac, Htac——余热吸收式制冷机t时刻对外供冷的功率和吸收的热功率;
COPac——AC的电热转换效能系数;
Itac——t时刻反应AC运行状态的0-1变量, Itac=1, AC处于运行状态, Itac=0, AC处于停运状态;
Hminac, Hmaxac——余热吸收式制冷机输入的最小热功率和最大热功率。
1.2.6 电制冷机模型
电制冷机模型为
| $ \left\{ \begin{array}{l} Q_t^{{\rm{ec}}} = {\rm{CO}}{{\rm{P}}^{{\rm{ec}}}}P_t^{{\rm{ec}}}\\ I_t^{{\rm{ec}}}P_{\min }^{{\rm{ec}}} \le I_t^{{\rm{ec}}}P_{\max }^{{\rm{ec}}} \end{array} \right. $ | (6) |
式中: Qtec, Ptec——电制冷机t时刻发出的冷功率和消耗的电功率;
COPec——电制冷机的电转冷效能系数;
Itec——t时刻反应电制冷机运行状态的0-1变量, Itec=1, 电制冷机处于运行状态, Itec=0, 电制冷机处于停运状态;
Pminec, Pmaxec——电制冷机电功率的最小值和最大值。
1.3 供能网络约束
1.3.1 配电网模型
园区配电系统通常呈辐射状运行。本文采用Distflow二阶锥模型[10]对其进行建模。
对于任意时刻, 园区配电网中任意节点j, 有以下功率平衡关系
| $ \left\{ \begin{array}{l} \sum\limits_{i \in \delta \left( j \right)} {\left( {{P_{ij}} - {r_{ij}}I_{ij}^2} \right) + {P_j} = \sum\limits_{k \in \pi \left( j \right)} {{P_{jk}}} } \\ \sum\limits_{i \in \delta \left( j \right)} {\left( {{Q_{ij}} - {x_{ij}}I_{ij}^2} \right) + {Q_j} = \sum\limits_{k \in \pi \left( j \right)} {{Q_{jk}}} } \\ {P_i} = P_i^{{\rm{chp}}} + P_i^{{\rm{grid}}} - P_i^{{\rm{eb}}} - P_i^{{\rm{hp}}} - P_i^{{\rm{ec}}}\\ {Q_i} = Q_i^{{\rm{chp}}} + Q_i^{{\rm{grid}}} - Q_i^{{\rm{load}}} \end{array} \right. $ | (7) |
式中: δ(j)——以j为末端节点的节点集合;
Pij, Qij——流过线路l(i, j)的有功和无功功率;
rij, xij——线路l(i, j)的电阻和电抗;
Iij——流过线路l(i, j)电流的幅值;
Pj, Qj——节点j注入的有功和无功功率;
π(j)——以j为首端节点的节点集合;
Pjk, Qjk——流过线路l(j, k)的有功和无功功率;
Pi, Qi——在节点i注入的有功和无功功率;
Pichp, Qichp——节点i处CHP机组的有功和无功出力;
Pigrid, Qigrid——节点i处上级配电网注入的有功和无功功率;
Piload, Qiload——负荷节点i处的有功和无功负荷;
Pieb, Pihp, Piec——在节点i处电锅炉、热泵和电制冷机消耗的有功功率。
对于任意时刻, 园区配电系统中任意支路l(i, j), 有以下关系成立
| $ U_j^2 = U_i^2 - 2\left( {{r_{ij}}{P_{ij}} + {x_{ij}}Q_{ij}} \right) + \left( {r_{ij}^2 + x_{ij}^2} \right)I_{ij}^2 $ | (8) |
| $ I_{ij}^2U_i^2 = P_{ij}^2 + Q_{ij}^2 $ | (9) |
| $ \left\{ \begin{array}{l} 0 \le {I_{ij}} \le {I_{ij}} ^u\\ U_i^1 \le {I_i} \le U_i^u \end{array} \right. $ | (10) |
式中: Iiju——Iij的最大值;
Ui1, Uiu——节点i的电压幅值Ui的上下限。
令ui=Ui2, iij=Iij2。将式(9)所表示的支路潮流约二次约束松弛为二阶锥形式, 即
| $ {i_{ij}}{u_{i}} \ge P_{ij}^2 + Q_{ij}^2 $ | (11) |
通过等价变换可表示为标准二阶锥形式, 即
| $ {\left\| \begin{array}{l} 2{P_{ij}}\\ 2{Q_{ij}}\\ {i_{ij}} - {u_i} \end{array} \right\|_2} \le {i_{ij}} - {u_i} $ | (12) |
支路潮流和节点电压约束分别为
| $ \left\{ \begin{array}{l} 0 \le {i_{ij}} \le {\left( {I_{ij}^{\rm{u}}} \right)^2}\\ {\left( {U_i^1} \right)^2} \le {u_i} \le {\left( {U_i^{\rm{u}}} \right)^2} \end{array} \right. $ | (13) |
式(7)、式(8)、式(11)、式(13)共同组成了辐射型配电网的Distflow二阶锥模型。
1.3.2 热网模型
供冷/供热系统主要包括冷/热源、冷/热负荷以及供冷/热网络。供冷系统的终端设备采用风机盘管, 供冷时, 供水管网将冷水从冷源送到冷负荷处, 冷水通过风机盘管传递热量后温度升高, 再经回水管网送回到冷源重新制冷。供热系统的终端设备采用换热器, 供热时, 供水管网将热水从热源送到热负荷处, 热水通过换热器传递热量后温度降低, 再经回水管网送回到热源重新制热。本文在文献[11-12]的基础上构建了线性冷/热网络模型。
对于任意节点j, 在任意时刻都满足以下冷/热功率平衡关系
| $ \left\{ \begin{array}{l} {\varphi _{o,i}} + \sum\limits_{j \in I} {\varphi {'_{ji}}} = 0\\ \varphi {'_{ij}} = - \left( {\varphi {'_{ji}} - \Delta \varphi {'_{ji}}} \right){\rm{if}}\varphi {'_{ji}} > 0\\ \varphi {'_{ij,\min }} \le \varphi {'_{ij}} \le \varphi {'_{ij,\max }}{\rm{if}}\varphi {'_{ij}} > 0 \end{array} \right. $ | (14) |
式中: φo, i——冷/热网中注入节点i处的冷/热功率;
I——热风中所有节点的集合;
φ′ij——供水管道s(i, j)流入节点i处的热媒可利用冷/热功率, 媒介从i流出时, φ′ij为负值, 反之则为正值;
Δφ′ji——热媒在管段内流动所产生的热能损失;
φ′ij, min, φ′ij, max——管段可传输的功率最小值和最大值。
| $ \left\{ {\Delta \varphi {'_{ij}} = 2\pi } \right.\frac{{{T_{\rm{s}}} - {T_{\rm{a}}}}}{{\sum R }}{l_{ij}} $ | (15) |
| $ \left\{ \begin{array}{l} \varphi {'_{ij, \max }} = 2\pi \frac{{{T_{\rm{s}}} - {T_{\rm{a}}}}}{{\sum R }}{l_{ij}}\\ \varphi {'_{ij, \max }} = {c_{\rm{w}}}{m_{ij}}\left( {{T_{\rm{s}}} - {T_{\rm{r}}}} \right) \end{array} \right. $ | (16) |
式中: Ts, Ta, Tr——供水、环境和回水的温度;
∑R——媒介到周围介质每千米管道热阻;
lij——管道(i, j)的长度;
cw——水的比热容;
mij——流过管道(i, j)的质量流量。
供热时, 对于节点i注入的热功率φs, i, 在任意时刻则满足
| $ \left\{ \begin{array}{l} {\varphi _{s,i}} = H_i^{{\rm{eb}}} + H_i^{{\rm{hp}}} + H_i^{{\rm{chp}}} + H_{{\rm{D}},i}^{{\rm{th}}} - \\ \;\;\;\;\;\;\;\;\;H_{{\rm{C}},i}^{{\rm{th}}} - H_I^{{\rm{ac}}} - H_i^{{\rm{load}}} \end{array} \right. $ | (17) |
式中: Hieb, Hihp, Hichp——节点i处电锅炉、热泵机组、CHP机组热输出功率;
HD, ith, HC, ith——蓄热罐放热、蓄热罐储热功率;
Hiac, Hiload——吸收式制冷机吸收热功率和热负荷功率。
同理, 供冷时, 对于节点i注入的冷功率φs, i, 在任意时刻则满足
| $ {\varphi _{s, i}} = Q_i^{{\rm{ec}}} + Q_i^{{\rm{ac}}} - Q_i^{{\rm{load}}} $ | (18) |
式中: Qiec, Qiac, Qiload——节点i处电制冷机、吸收式制冷机的冷输出功率和冷负荷功率。
2 园区型电—热综合能源系统能源站双层优化配置模型
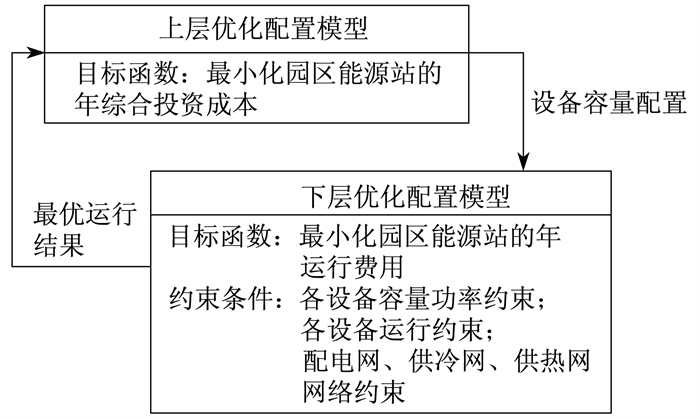
本文构建的电-热综合能源系统双层优化配置模型中, 上层模型以园区IES的年综合投资成本最小为目标, 对系统内各设备的容量进行优化配置, 下层模型基于上层模型设备容量配置的结果, 以年运行费用最小为目标, 对系统内机组的功率输出进行优化。最后, 上下两层模型交替迭代, 得出能源站最优的配置方案。
其优化框架如图 2所示。
2.1 上层优化配置模型
上层优化配置模型以园区IES能源站总投资的年化总费用最小为目标。该费用包括设备初始投资等年值费用、设备运行维护成本、购气费用和购电费用。
| $ \min \;\;C_{\sum {} }^{{\rm{ann}}} = C_{{\rm{inv}}}^{{\rm{ann}}} + C_{{\rm{om}}}^{{\rm{ann}}} + C_{{\rm{grid}}}^{{\rm{ann}}} + C_{{\rm{gas}}}^{{\rm{ann}}} $ | (19) |
式中: CΣann——年化总费用;
Cinvann——设备初始投资等年值费用;
Comann——设备年运行维护成本;
Cgasann——年天然气购买成本;
Cgridann——从上级电网的年购电费用。
设备初始投资等年值费用的数学表达式为
| $ C_{{\rm{inv}}}^{{\rm{ann}}} = {\sum\limits_{i = 1}^{{N_{{\rm{inv}}}}} {\frac{{r\left( {1 + r} \right)}}{{{{\left( {1 + r} \right)}^\tau } - 1}}} ^\tau }{X_i}{c_i} $ | (20) |
式中: Ninv——系统中设备的总数;
r——折现率, 取6.67%;
τ——设备的生命周期, 取20 a;
Xi——第i种设备的配置容量;
ci——第i种设备的单位初始投资成本, 元/kW。
上层优化配置模型中系统各设备容量的优化配置向量为
| $ X = {\left( {{X_{{\rm{chp}}}}, {X_{{\rm{th}}}}, {X_{{\rm{ec}}}}, {X_{{\rm{ac}}}}, {X_{{\rm{eb}}}}, {X_{{\rm{hp}}}}} \right)^{\rm{T}}} $ | (21) |
式中: Xchp, Xth, Xec——系统内CHP机组、蓄热罐、电制冷机所配置的容量;
Xac, Xeb, Xhp——系统内余热吸收式制冷机、电锅炉、热泵机组所配置的容量。
2.2 下层优化运行模型
本文基于某科创园区的基础负荷数据, 取春秋季、夏季和冬季各一个典型日的冷、电、热负荷功率曲线。下层优化调度模型的优化变量Y(t)包括: t时刻的购电功率Ptgrid, CHP机组输出的电和热功率Ptchp和Htchp, 蓄热罐的吸热和放热功率HC, tth和HD, tth, 电制冷机的电功率和制冷功率Ptec和Qtec, 余热吸收式制冷机的吸热功率和制冷功率HC, tac和QD, tac, 电锅炉的电功率和热输出功率Pteb和Hteb, 热泵的电功率和热输出功率Pteb和Hthp。
下层优化的目标函数为
| $ \begin{array}{l} \min \sum\limits_{i = 1}^S {{D_i}} \left\{ {\sum\limits_{t = 1}^{24} {{c_{{\rm{grid}}}}P_t^{{\rm{grid}}} + {c_{{\rm{gas}}}}V_t^{{\rm{chp}}} + {\varepsilon _{{\rm{chp}}}}P_t^{{\rm{chp}}} + } } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\varepsilon _{{\rm{ec}}}}P_t^{{\rm{ec}}} + {\varepsilon _{{\rm{th}}}}\left( {Q_{{\rm{C}}, t}^{{\rm{th}}} + Q_{{\rm{D}}, \mathit{t}}^{{\rm{th}}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\varepsilon _{{\rm{ac}}}}Q_t^{{\rm{ac}}} + {\varepsilon _{{\rm{eb}}}}P_t^{{\rm{eb}}} + {\varepsilon _{{\rm{hp}}}}P_t^{{\rm{hp}}}\left. {} \right\}\Delta T \end{array} $ | (22) |
式中: S——供能季节, 本文取3;
Di——第i个供能季节的持续天数;
cgrid, cgas——分时电价和天然气价;
εchp, εec, εth——CHP机组、电制冷机和蓄热罐的单位运行维护成本, 元/kW;
εac, εeb, εhp——余热吸收式制冷机、电锅炉以及热泵的单位运行维护成本, 元/kW。
2.3 模型求解
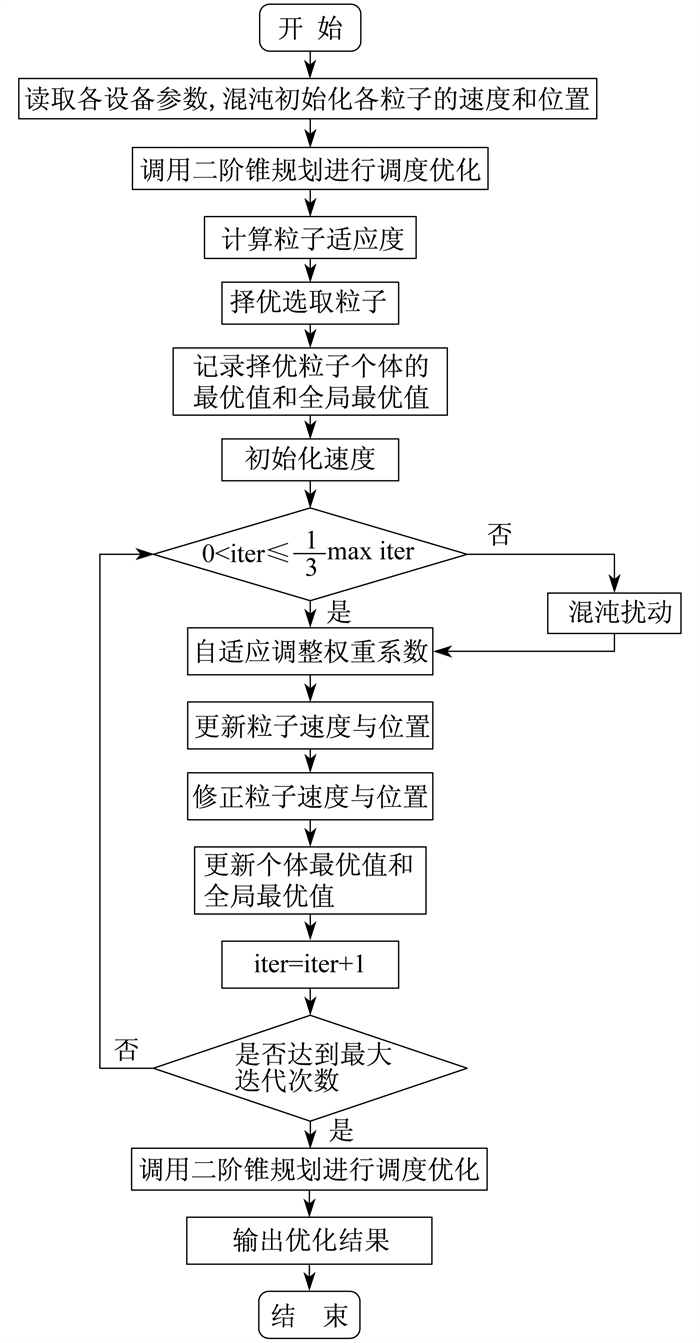
针对本文构建的双层优化配置模型, 为提高上层模型的全局收敛性, 采用文献[13]的自适应混沌粒子群算法对上层设备容量优化配置; 下层模型在MATLAB环境中利用YALMIP工具箱, 调用商业求解器GUROBI进行求解。在求解本文的双层优化配置模型过程中, 上层模型中的一个粒子对应一种设备容量优化配置方案, 上层模型设备容量的优化配置结果带入下层优化调度模型, 并计算出该配置方案下系统设备的年运行维护成本、年购电费用和年购气费用, 并返回给上层模型的粒子。粒子的适应度由设备初始投资等年值费用和上层模型所计算出的费用相加得到。基于自适应混沌粒子群算法进行系统优化配置方案的寻优, 得出最后的全局最优解。
本文模型的求解流程如图 3所示。
3 算例分析
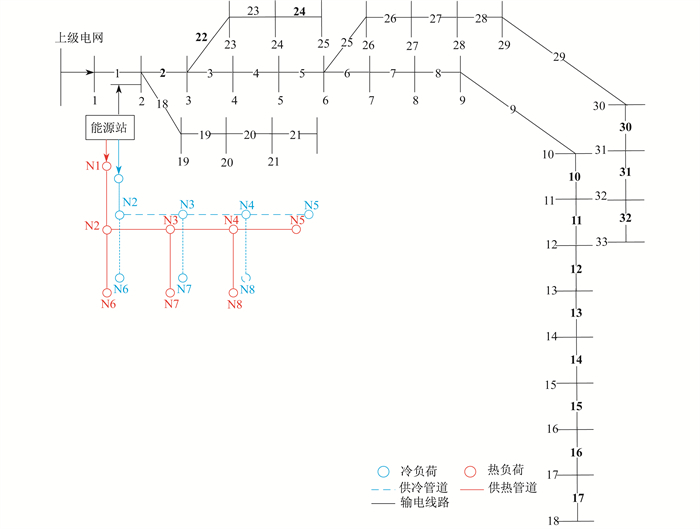
本文算例是在文献[14]算例基础上改进而来的, 为IEEE-33节点配电网和8节点区域冷/热网组成的综合能源系统。其拓扑图如图 4所示。
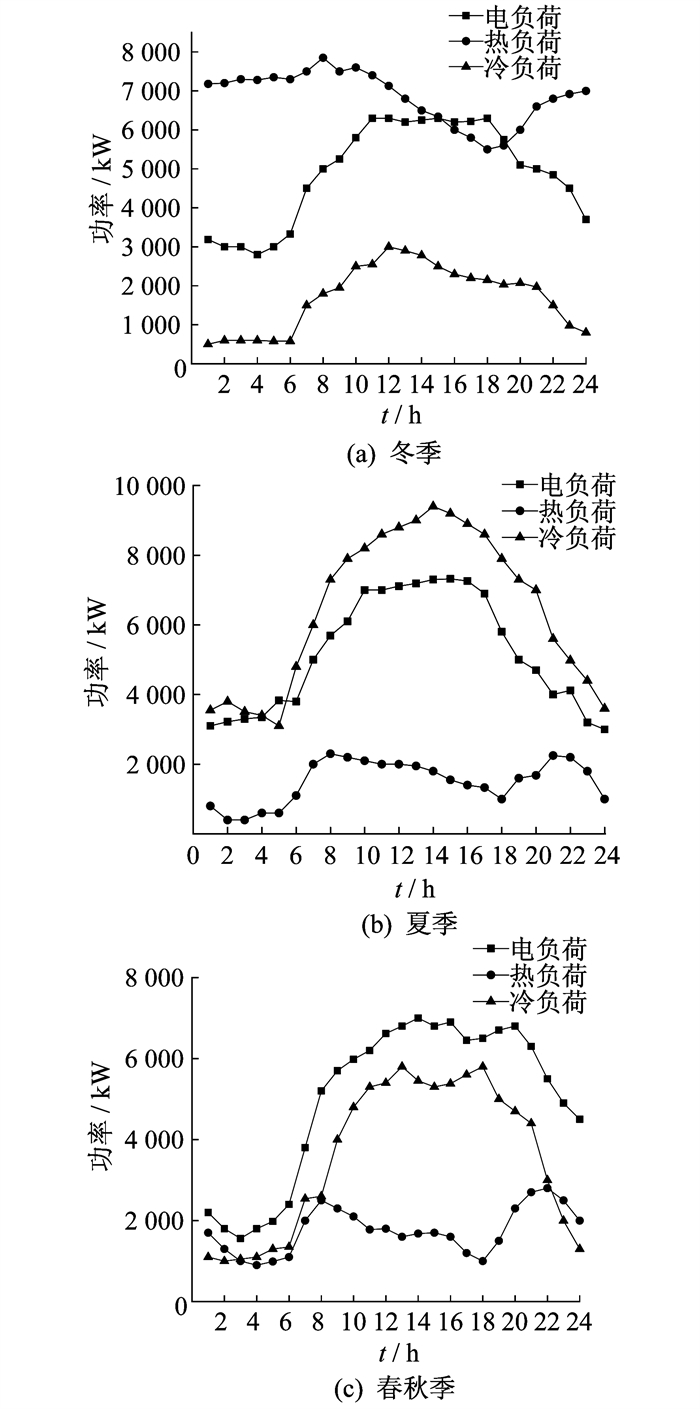
各供能设备的参数[15-17]如表 1所示。冬季、夏季和春秋季典型日冷、热、电负荷曲线如图 5所示。在自适应混沌粒子群算法中, 设粒子群数量N=50, 且最大迭代次数为100次。
表 1
设备参数
| 设备类型 | 能源转换效率 | 热电比 | 初始投资成本 | 运行维护成本 | 寿命/a |
| (元·kW-1) | |||||
| CHP机组 | 0.36 | 1.5 | 6 000 | 0.060 | 20 |
| 蓄热罐 | 0.95 | / | 200 | 2.430 | 20 |
| 电制冷机 | 2.40 | / | 970 | 0.097 | 10 |
| 余热吸收式制冷机 | 1.34 | / | 1 100 | 0.080 | 20 |
| 电锅炉 | 0.98 | / | 200 | 0.174 | 10 |
| 热泵机组 | 2.50 | / | 300 | 0.150 | 15 |
为验证所提模型的有效性, 本文在考虑供能网络约束的条件下, 对3个方案的综合能源系统优化配置问题进行分析。
方案1:天然气价格取2.83元/m3, 电价采用工商业分时电价[18], 每天9:00~12:00和17:00~21:00为峰时段, 峰时电价0.798 0元/kWh; 00:00~8:00和23:00~24:00为低谷时段, 谷时电价0.315 3元/kWh; 8:00~9:00, 12:00~17:00, 22:00~23:00为平时段, 平时电价0.598 3元/kWh。同时, 配置方案的功能设备中不采用热泵机组。
方案2:在方案1的基础上, 加入热泵机组。
方案3:在方案2的基础上, 电价采用居民分时电价, 07:00~20:00电价为0.49元/kWh, 其余时段电价为0.30元/kWh。
3.1 优化配置结果
表 2为3种方案下系统设备容量的配置结果和系统的年总费用。
表 2
机组容量配置结果和系统年总费用
| 方案 | 配置容量/kW | 年总费用/万元 | |||||
| CHP | TS | EC | EB | 热泵 | AC | ||
| 1 | 4 327 | 7 182 | 2 483 | 0 | 0 | 8 227 | 3 547.24 |
| 2 | 4 211 | 7 059 | 1 894 | 0 | 805 | 5 173 | 3 470.81 |
| 3 | 3 393 | 6 209 | 7 218 | 0 | 1 687 | 3 372 | 3 109.47 |
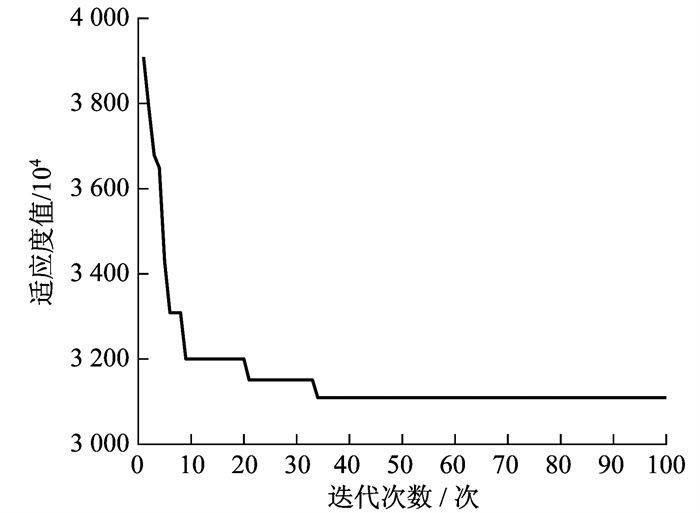
由表 2可以看出, 方案1中, 为满足不同季节园区用户的冷、热、电负荷需求, 需配置一定容量的CHP机组和热泵机组来满足冬季供热的需求, 配置一定容量的余热吸收式制冷机(AC)和电制冷机(EC)来满足供冷的需求。由于工商业电价相对较高且电锅炉(EB)的电转热效率不高, 在方案1的优化配置中没有配置电锅炉。方案3的配置结果迭代曲线如图 6所示。由图 6可以看出, 算法达到了全局最优性, 验证了混沌自适应粒子群优化算法的有效性。
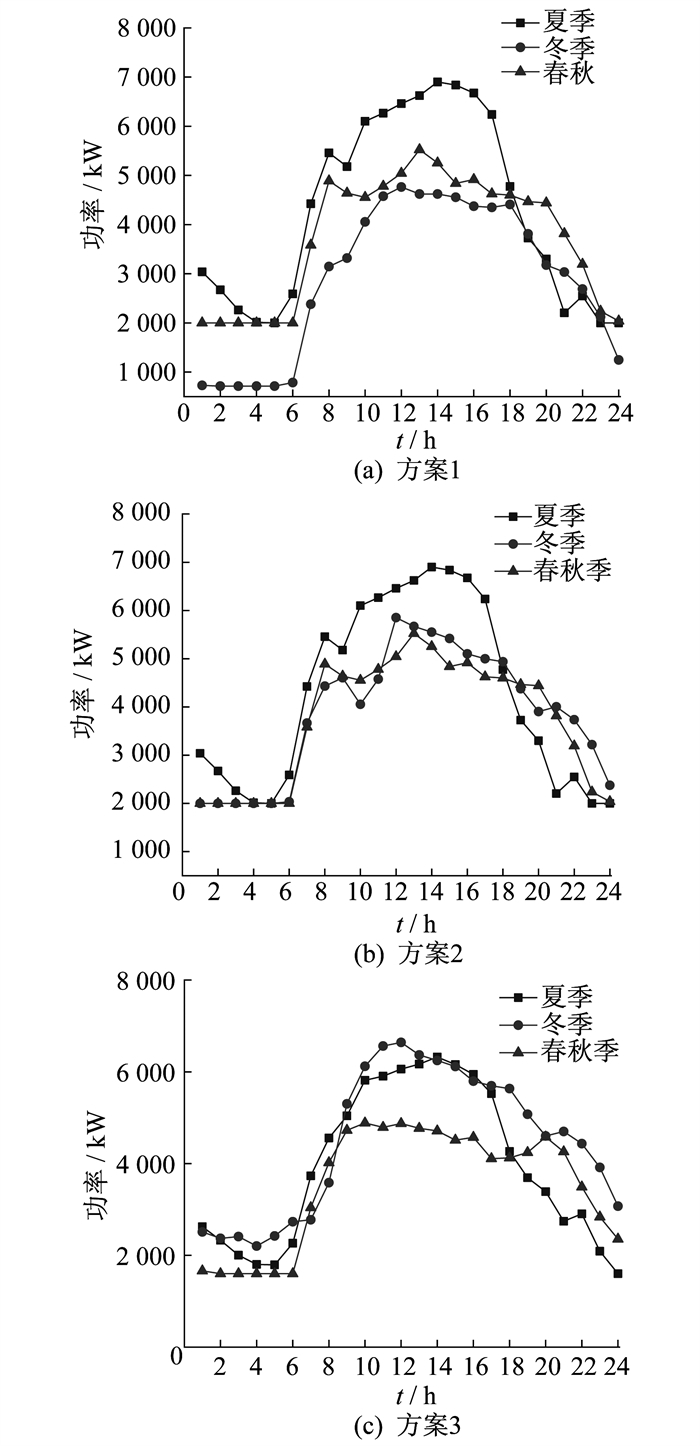
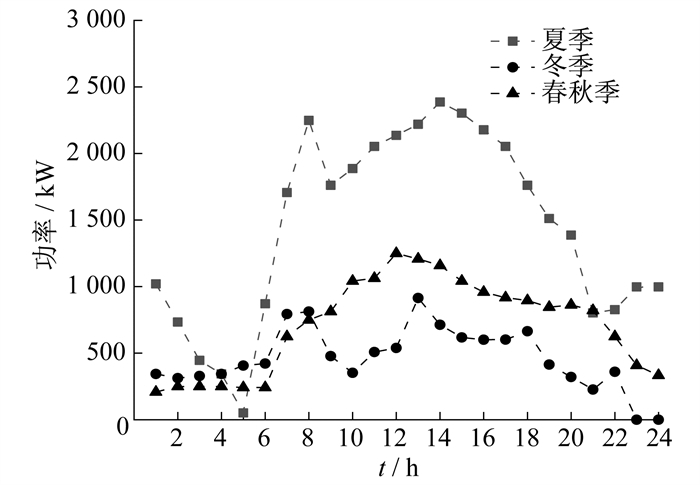
图 7为3种方案下系统的购电功率曲线, 图 8为方案1中电制冷机的电功率曲线。由图 7和图 8可以看出, 随着用户的供冷需求加大, 需要由电制冷设备(如电制冷机)来进行供冷, 夏季对供冷需求尤为迫切, 需要电制冷加大供冷量, 导致系统从上级电网采购的电功率增多, 系统电负荷加重, 从而给配电网的运行带来一定压力。在冬季, 由于系统内配置了一定容量的CHP机组, CHP机组可进行热电联产, 向系统供热的同时也提供一部分电功率, 因而可以在一定程度上缓解系统的购电压力。
此外, 由表 2可以看出, 方案2因系统采用电转热效率相对较高的热泵机组辅助供热, 提高了能源的转换效率, 节省了电能, 导致CHP机组的配置容量较方案1虽变化不大, 但总成本却有了一定程度的下降。且由图 7可以看出, 方案2中夏、春秋季系统的购电功率与方案1相同, 而冬季的购电功率相比方案1有了一定的增加。
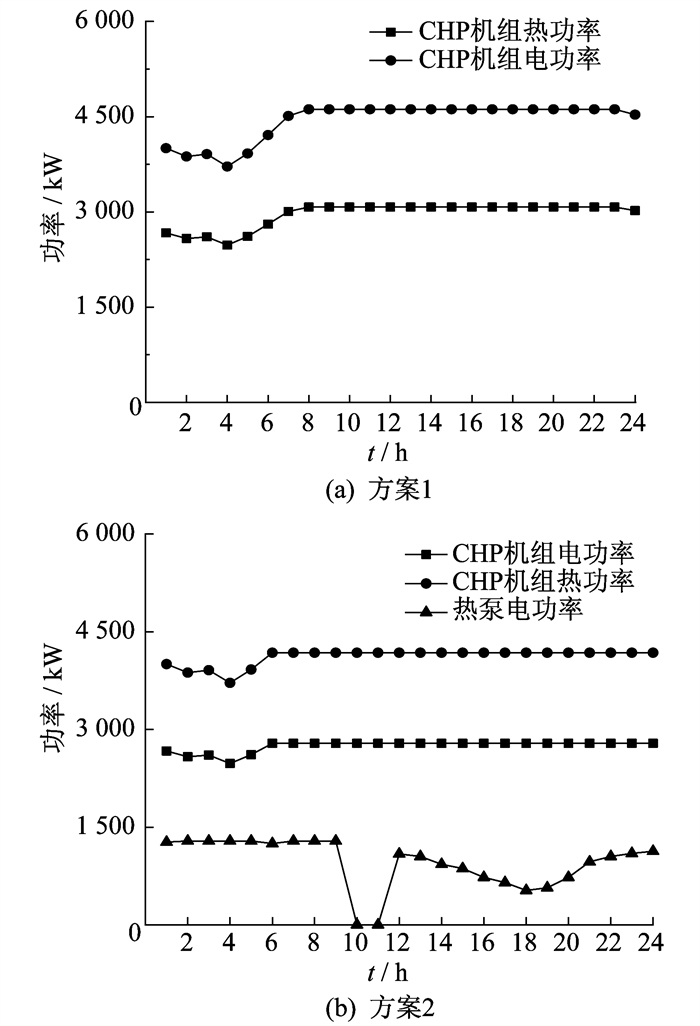
图 9为方案1和方案2中CHP机组和热泵机组在冬季的功率曲线。
由图 9可以看出, 在冬季, 热泵机组可以辅助供热, 承担一部分系统的热负荷, 从而导致CHP机组的供电和供热空间受到压缩, 同时在一定程度上加重了系统的电负荷。
结合图 7和表 2可以看出, 在方案3居民电价的调节下, 热泵机组较电锅炉电转热效率要高的优势得以体现, 热泵机组可在供热需求方面代替一部分CHP机组的配置容量, 可以有效地降低系统的购气成本, 且方案3的年总费用较方案1和方案2均有了较大程度的下降。此外, 与方案2相比, 在价格更低的居民电价的作用下, 热泵机组容量配置加大, 使得方案3中系统的冬季用电量有了明显的提升, 在冬季供热需求高峰时段甚至超过了相同时段下的夏季用电负荷。
3.2 供能网络约束对系统投资成本和总成本的影响
为了考虑供能网络约束对系统年总费用的影响, 在方案2的基础上, 分析对比了3种场景下系统的年总费用, 结果如表 3所示。
表 3
方案2下3种场景的年总费用对比
| 场景 | 冷/热网 | 电网 | 设备年投资费用 | 年运行费用 | 年总费用 |
| 1 | 无 | 无 | 303.38 | 3 522.99 | 3 826.37 |
| 2 | 无 | 有 | 269.07 | 3 410.17 | 3 679.24 |
| 3 | 有 | 有 | 239.45 | 3 231.46 | 3 470.81 |
由表 3可以看出, 场景3考虑了配电网和供冷/热网约束后, 设备的年投资费用较场景2和场景1同比减小了11.00%和22.06%, 系统的年总费用较场景2和场景1同比减小了5.67%和9.29%。由于考虑了配电网和供冷/热网的网络约束, 以及冷、热、电相互转换过程中多元能流在供能网络中的传输特性, 因此场景3实现了多元能源在供能网络中的最优分布, 实现了设备容量的优化配置, 减小了系统设备的投资成本、运行成本和总成本。
4 结论
本文面向园区型电-热综合能源系统的能源供应需求, 提出了一种考虑供能网络约束的园区综合能源系统能源站双层优化配置模型。通过具体的算例分析, 得出以下结论。
(1) CHP机组可以进行热电联产, 对能源的利用效率相对较高, 在园区型综合能源系统中有着较好的应用前景; 空气源热泵凭借其较高的能源转换效率, 在电转热领域有着广泛的应用。
(2) 能源价格对园区内综合能源系统的供能设备配置方案有较大的影响, 能源价格一定程度的变化会导致系统内不同负荷的相互转换。
(3) 考虑系统中供能网络的网络特性约束, 可以实现系统中多元能流的最优分布, 优化机组的配置容量, 减小系统的总费用。
(4) 系统中冷、热、电负荷具有不确定性, 同时系统中还可以考虑加入风光等间歇性分布式电源, 而这些元素的不确定性会给系统的优化配置产生一定的影响。后续将围绕风光和冷、热、电多元负荷的不确定性进行深入研究。不同优化算法有可能对配置的结果产生影响, 不同收敛性的优化算法求解的配置结果的对比也是后续研究的一个方面。
参考文献
-
[1]马钊, 周孝信, 尚宇炜, 等. 能源互联网概念、关键技术及发展模式探索[J]. 电网技术, 2015, 39(11): 3014-3022.
-
[2]余晓丹, 徐宪东, 陈硕翼, 等. 综合能源系统与能源互联网简述[J]. 电工技术学报, 2016, 31(1): 1-13. DOI:10.3969/j.issn.1000-6753.2016.01.001
-
[3]王丹, 智云强, 贾宏杰, 等. 基于多能源站协调的区域电力——热力系统日前经济调度[J]. 电力系统自动化, 2018, 42(13): 59-67. DOI:10.7500/AEPS20171129003
-
[4]周灿煌, 郑杰辉, 荆朝霞, 等. 面向园区微网的综合能源系统多目标优化设计[J]. 电网技术, 2018, 42(6): 1687-1697.
-
[5]徐航, 董树锋, 何仲潇, 等. 考虑能量梯级利用的工厂综合能源系统多能协同优化[J]. 电力系统自动化, 2018, 42(14): 123-130. DOI:10.7500/AEPS20170825006
-
[6]CHEN X, KANG C, MALLEY M O, et al. Increasing the flexibility of combined heat and power for wind power integration in China: modeling and implications[J]. IEEE Transactions on Power Systems, 2015, 30(4): 1848-1857. DOI:10.1109/TPWRS.2014.2356723
-
[7]陈沼宇, 王丹, 贾宏杰, 等. 考虑P2G多源储能型微网日前最优经济调度策略研究[J]. 中国电机工程学报, 2017, 37(11): 3067-3077.
-
[8]刘蓉晖, 马天天, 高远, 等. 考虑需求侧协同响应的社区综合能源系统低碳经济调度[J]. 上海电力大学学报, 2020, 36(5): 421-430. DOI:10.3969/j.issn.2096-8299.2020.05.002
-
[9]王伟亮, 王丹, 贾宏杰, 等. 考虑运行约束的区域电力-天然气-热力综合能源系统能量流优化分析[J]. 中国电机工程学报, 2017, 37(24): 7108-7120.
-
[10]邢海军, 程浩忠, 曾平良, 等. 基于二阶锥规划的间歇性分布式电源消纳研究[J]. 电力自动化设备, 2016, 36(6): 74-80.
-
[11]顾伟, 陆帅, 王珺, 等. 多区域综合能源系统热网建模及系统运行优化[J]. 中国电机工程学报, 2017, 37(5): 1305-1316.
-
[12]林舜江, 杨智斌, 卢苑, 等. 含光伏的天然气冷热电联供园区微网能量优化调度[J]. 华南理工大学学报(自然科学版), 2019, 47(3): 9-19.
-
[13]郭伟. 基于ACPSO算法的分布式电源优化配置研究[D]. 长沙: 长沙理工大学, 2013.
-
[14]LI J, FANG J, ZENG Q, et al. Optimal operation of the integrated electrical and heating systems to accommodate the intermittent renewable sources[J]. Applied Energy, 2016, 167: 244-254. DOI:10.1016/j.apenergy.2015.10.054
-
[15]范宏, 袁倩倩, 邓剑. 多区域综合能源系统的两阶段容量优化配置方法[J]. 现代电力, 2020, 37(5): 441-449.
-
[16]王婉璐, 杨莉, 王蕾, 等. 考虑供热网储热特性的电-热综合能源系统优化调度[J]. 电力系统自动化, 2018, 42(21): 45-55. DOI:10.7500/AEPS20170908013
-
[17]唐沂媛. 冷热电联供/综合能源系统的规划研究[D]. 南京: 东南大学, 2016.
-
[18]郭尊, 李庚银, 周明, 等. 计及综合需求响应的商业园区能量枢纽优化运行[J]. 电网技术, 2018, 42(8): 2439-2448.