|
|
|
发布时间: 2021-10-28 |
清洁安全发电 |
|
|
|
收稿日期: 2020-03-24
基金项目: 国家自然科学基金(61401269,61572311);上海市科技创新行动计划地方院校能力建设项目(17020500900)
中图法分类号: TM614
文献标识码: A
文章编号: 2096-8299(2021)05-0415-07
|
摘要
由于风光能源具有间歇性和波动性的特点,对电网的电能质量造成了不良影响,因此提出了一种微电网的储能容量优化配置方法。首先,建立以用户用电费用最低、储能能量损失最小及风光能源的波动性最小为目标的微电网系统模型;然后,提出了一种改进的人工蜂群算法求解模型,通过不同的算法对无储能、单储能及混合储能3种储能方案模型进行求解分析;最后,采用熵权法找出适用于微电网的最佳储能方案。实验结果表明,改进的人工蜂群算法能够求解微电网模型且不易陷入局部最优,并通过熵权法得出了蓄电池和超级电容的组合适合作为微电网储能系统的结论。
关键词
微电网; 多目标优化; 人工蜂群算法; 熵权法
Abstract
The intermittent and fluctuating characteristics of wind and solar energy causes adverse effects on the power quality of the power grid, so this paper proposes a method for the optimal configuration of the energy storage capacity of the micro grid.Firstly, a microgrid system model with the lowest user electricity cost, the smallest energy loss from energy storage, and the smallest volatility of wind and solar energy is established.Then an improved artificial bee colony algorithm solution model is proposed.Three energy storage scheme models of no energy storage, single energy storage and hybrid energy storage are solved and analyzed.Finally, the entropy weight method is used to find the best energy storage scheme for the microgrid.The experimental results show that the improved artificial bee colony algorithm can solve the microgrid model and is not easy to fall into the local optimum, and the combination of battery and supercapacitor is obtained through the entropy weight method as the microgrid energy storage system.
Key words
microgrid; multi-objective; artifical bee colony; entropy weight method
随着不可再生能源短缺以及环境污染等问题的日益严峻, 光伏和风电能源得到了大力发展[1]。因容易受到天气的影响, 风、光能源具有随机性和不确定性的特点, 而储能装置能够解决其所造成的功率波动问题, 提高风光能源的渗透率, 因此储能装置在微电网系统中占据了重要位置[2-3]。储能装置分为功率型和能量型两种, 微电网系统中通常利用混合储能的优势来提高储能系统的性能[4]。由于储能成本的造价较高, 因此需要合理地配置储能设备, 既要保证微电网系统正常运行, 又要保证其经济性[5]。对于储能系统容量的优化配置, 已有许多文献做出了相应的研究。文献[6]建立的混合储能系统是以年综合成本最小为目标的模型, 但仅考虑了系统的经济性。文献[7]建立了储能系统的多目标优化模型, 但不同目标的权重仅为主观设定。文献[8]用滑动平均法得到了并网的功率, 并利用蓄电池和超级电容来平衡原始功率与并网功率之间的差值功率。上述文献大多以微电网系统的经济效益高、风光能源的波动性小为目标, 但均未考虑储能充放电过程中造成的能量损失, 且未对微电网的不同储能配置方案加以对比和分析。
在以上文献研究的基础上, 本文建立了储能系统优化配置模型。利用粒子群算法、人工蜂群算法及改进的人工蜂群算法来验证模型的有效性, 并对混合储能、单一储能以及无储能3种方案的优化结果进行比较。另外, 由于不同指标的量纲不同, 因此本文提出利用熵权法来确定最佳的储能配置方案。
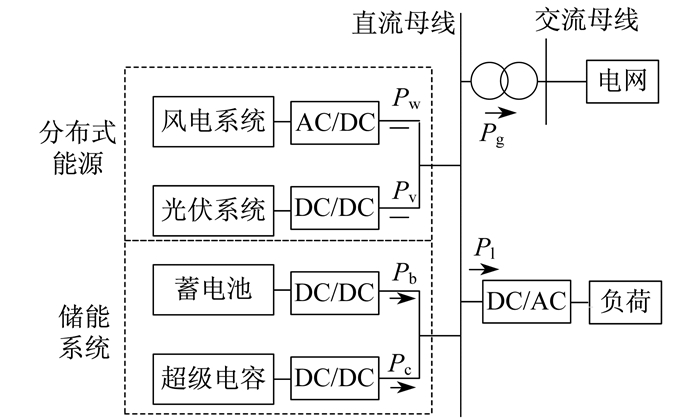
1 并网式微电网系统
2 小波包分析
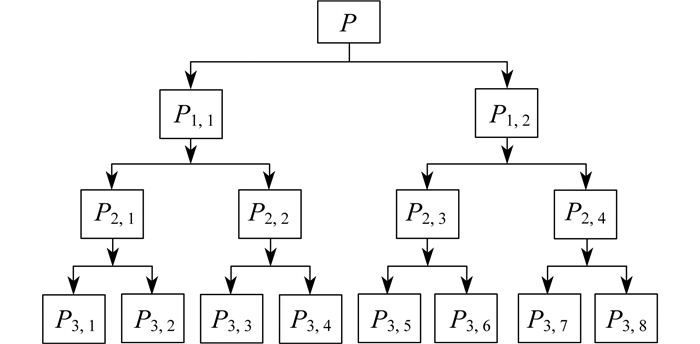
由于风光能源的特点, 所以其产生的有功功率具有较大的波动性。如果不作处理, 则对大电网和用户都会造成不良的影响[10]。小波分析能够减小信号的波动性, 适用于对非平稳突变信号的处理, 但其存在的缺陷是只对分解后的低频信号再次分解, 而对高频信号不作处理。小波包分析是对小波分析的完善, 其对高频信号也进行了分解[11]。3层小波包分解原理如图 2所示。
风光能源分解后的直流分量由联络线或负荷用电承担, 剩下的由蓄电池和超级电容进行补偿。分解的层数决定了风光功率波动的程度, 当分解层数为n时, Pn, 1为供给用户使用的功率或作为联络线上的交互功率。用nBC表示蓄电池和超级电容频率分界点, 则蓄电池和超级电容的功率分配公式为
| $ \left\{\begin{array}{l} P_{\mathrm{b}}=P_{n, 2}+P_{n, 3}+\cdots+P_{n, n_{\mathrm{bc}}} \\ P_{\mathrm{c}}=P_{n, n_{\mathrm{bc}}+1}+P_{n, n_{\mathrm{bc}}+2}+\cdots+P_{n, 2^{n}} \end{array}\right. $ | (1) |
式中: Pn, i——分解层次数为n时, 由蓄电池和超电容补偿的风光功率, n为自然数, i=2, 3, 4, …, 2n。
3 储能配置的优化目标
本文综合考虑用户每日承担的费用、风光能源的波动性以及储能的能量损失3个因素, 建立了微电网储能配置系统模型, 具体的计算模型如下。
3.1 经济模型
配置储能系统时, 在保证微电网正常运行的前提下, 要使用户每日承担的费用最低。为了更精确地计算成本[12], 将用户承担的费用折算成每日的微电网系统投资初始费用、维护费用和购售电费用3个部分, 其公式为
| $ \begin{aligned} f_{1}=&C_{\mathrm{pv} 1}+C_{\mathrm{w} 1}+C_{\mathrm{ess} 1}+C_{\mathrm{pv} 2}+ \\ &C_{\mathrm{w} 2}+C_{\mathrm{ess} 2}+C_{\mathrm{g}} \end{aligned} $ | (2) |
式中: f1——用户每日承担的经济费用;
Cpv1——每日光伏初始投资费用;
Cw1——每日风机初始投资费用;
Cess1——每日储能系统的投资费用;
Cpv2——每日光伏的维护费用;
Cw2——每日风机的维护费用;
Cess2——每日储能系统的维护费用;
Cg——购买电和出售电的费用和。
| $ \left\{\begin{array}{l} C_{\mathrm{pv1}}= C_{\mathrm{pv}} P_{\mathrm{v}} \frac{r(1+r)^{n_{\mathrm{pv}}}}{365\left[(1+r)^{n_{\mathrm{pv}}}-1\right]} \\ C_{\mathrm{w} 1}= C_{\mathrm{w}} P_{\mathrm{w}} \frac{r(1+r)^{n_{\mathrm{w}}}}{365\left[(1+r)^{n_{\mathrm{w}}}-1\right]} \\ C_{\mathrm{ess1}}= \frac{1}{365}\left[\left(C_{1} E_{\mathrm{b}}+C_{2} P_{\mathrm{b}}\right) \frac{r(1+r)^{n_{\mathrm{b}}}}{(1+r)^{n_{\mathrm{b}}}-1}+\right.\\ \qquad\quad\left.\left(C_{3} E_{\mathrm{c}}+C_{4} P_{\mathrm{c}}\right) \frac{r(1+r)^{n_{\mathrm{c}}}}{(1+r)^{n_{\mathrm{c}}}-1}\right] \end{array}\right. $ | (3) |
| $ \left\{\begin{array}{l} C_{\mathrm{pv} 2}=C_{\mathrm{mp}} P_{\mathrm{v}} \frac{r(1+r)^{n_{\mathrm{pv}}}}{365\left[(1+r)^{n_{\mathrm{pv}}}-1\right]} \\ C_{\mathrm{w} 2}=C_{\mathrm{mw}} P_{\mathrm{w}} \frac{r(1+r)^{n_{\mathrm{w}}}}{365\left[(1+r)^{n_{\mathrm{w}}}-1\right]} \\ C_{\mathrm{ess} 2}=\frac{1}{365}\left[C_{\mathrm{mb}} P_{\mathrm{b}} \frac{r(1+r)^{n_{\mathrm{b}}}}{(1+r)^{n_{\mathrm{b}}}-1}+\right. \\ \qquad\quad\left. C_{\mathrm{mc}} P_{\mathrm{c}} \frac{r(1+r)^{n_{\mathrm{c}}}}{(1+r)^{n_{\mathrm{c}}}-1}\right] \\ C_{\mathrm{g}}=\sum\limits_{t=1}^{T} R_{\mathrm{g}} P_{\mathrm{g}}(t) \Delta t \end{array}\right. $ | (4) |
式中: Cpv——光伏单位功率成本系数;
r——设备折旧率;
npv——光伏的使用年限;
Cw——风机单位功率成本系数;
nw——风机的使用年限;
C1——蓄电池单位功率成本系数;
Eb——蓄电池的额定容量;
C2——蓄电池单位容量成本系数;
Pb——蓄电池的额定功率;
nb——蓄电池的使用年限;
C3——超级电容单位功率成本系数;
Ec——超级电容的额定容量;
C4——超级电容单位容量成本系数;
Pc——超级电容的额定功率;
nc——超级电容的使用年限;
Cmp——光伏单位功率维护成本系数;
Cmw——风机单位功率维护成本系数;
Cmb——蓄电池单位功率维护成本系数;
Cmc——超级电容单位功率维护成本系数;
Rg——不同时刻的电价;
Pg(t)——t时刻用户与电网的交互功率;
Δt——采样点间隔。
3.2 储能能量损失模型
储能系统在电能调度过程中, 容易产生能量损失, 造成资源浪费, 因此在微电网正常运行的基础上, 也要保障能量损失最小。储能能量损失的计算公式为
| $ \begin{aligned} f_{2}=& \sum\limits_{t=1}^{T}\left[P_{\mathrm{bch}}(t) \frac{1-\eta_{\mathrm{bch}}}{\eta_{\mathrm{bch}}} \Delta t+\right.\\ &\left.P_{\mathrm{bdis}}(t)\left(1-\eta_{\mathrm{bdis}}\right) \Delta t\right]+\\ & \sum\limits_{t=1}^{T}\left[P_{\mathrm{cch}}(t) \frac{1-\eta_{\mathrm{cch}}}{\eta_{\mathrm{cch}}} \Delta t+\right.\\ &\left.P_{\mathrm{cdis}}(t)\left(1-\eta_{\mathrm{cdis}}\right) \Delta t\right] \end{aligned} $ | (6) |
式中: T——一日的数据采样点个数;
Pbch(t), Pbdis(t)——t时刻蓄电池的充电功率和放电功率;
ηbch, ηbdis——蓄电池的充电效率和放电效率;
Pcch(t), Pcdis(t)——t时刻超级电容的充电功率和放电功率;
ηcch, ηcdis——超级电容的充电效率和放电效率。
3.3 风光综合功率波动模型
风光能源综合功率的波动采用经混合储能平抑前后功率变化差值的平方与初始功率的比值来表示, 其公式为
| $ \left\{\begin{array}{l} f_{3}=\frac{\sum\limits_{t=1}^{T}\left[P_{\mathrm{DG}}(t)-P_{\mathrm{DG}}(t-1)\right]^{2}}{\sum\limits_{t=1}^{T} P_{\mathrm{DG}}(t)} \\ P(t)=P_{\mathrm{v}}(t)+P_{\mathrm{w}}(t) \\ P_{\mathrm{DG}}(t)=P(t)+P_{\mathrm{b}}(t)+P_{\mathrm{c}}(t) \end{array}\right. $ | (7) |
式中: f3——风光能源的综合功率的波动水平;
PDG(t)——t时刻混合储能补偿后风光能源的综合功率;
P——风光综合功率。
3.4 约束条件
(1) 微电网系统功率平衡约束微电网在正常运行过程中, 要保证各个组成部分所产生的功率平衡。
| $ P_{1} \mathrm{~L}=P_{\mathrm{v}}+P_{\mathrm{w}}+P_{\mathrm{b}}+P_{\mathrm{c}}+P_{\mathrm{g}} $ | (8) |
(2) 储能系统的约束为了保证储能系统的正常运行, 储能的充放电功率在任意时刻应满足在一定的范围内。另外, 储能电池的荷电状态(State of Charge, SOC)表示剩余能量与额定容量的比值。为了延长储能电池的寿命, 要保证荷电状态在允许的范围内。
| $ \begin{gathered} P_{\mathrm{b}, \min } \leqslant P_{\mathrm{b}}(t) \leqslant P_{\mathrm{b}, \max } \\ P_{\mathrm{c}, \min } \leqslant P_{\mathrm{c}}(t) \leqslant P_{\mathrm{c}, \max } \end{gathered} $ | (9) |
| $ \left\{\begin{array}{l} \mathrm{SOC}_{\mathrm{b}, \min } \leqslant \operatorname{SOC}_{\mathrm{b}}(t) \leqslant \mathrm{SOC}_{\mathrm{b}, \max } \\ \mathrm{SOC}_{\mathrm{c}, \min } \leqslant \operatorname{SOC}_{\mathrm{c}}(t) \leqslant \mathrm{SOC}_{\mathrm{c}, \mathrm{max}} \end{array}\right. $ | (10) |
(3) 联络线交换功率约束联络线上的交互功率应在系统运行所允许的交换限制以内, 从而保证微电网的稳定运行。
| $ P_{\mathrm{g}, \min } \leqslant P_{\mathrm{g}}(t) \leqslant P_{\mathrm{g}, \max } $ | (11) |
(4) 风光能源的功率约束光伏和风机产生的功率需满足在一定的上下限功率范围内。
| $ \left\{\begin{array}{l} P_{\mathrm{v}, \min } \leqslant P_{\mathrm{v}}(t) \leqslant P_{\mathrm{v}, \max } \\ P_{\mathrm{w}, \min } \leqslant P_{\mathrm{w}}(t) \leqslant P_{\mathrm{w}, \max } \end{array}\right. $ | (12) |
4 储能系统规划优化算法
目前, 常见的群体智能优化算法包括人工蜂群算法、遗传算法、粒子群算法及细菌觅食算法等[13]。其中人工蜂群算法较为简单, 全局搜索能力好, 鲁棒性强, 但也存在着易于陷入局部最优的问题。为了提高算法的性能, 本文提出了在位置更新公式中引入全局因子的方法。在保留人工蜂群算法良好的全局搜索能力的前提下, 本文算法提高了局部搜索能力, 加快了收敛速度, 并且可以实现对微电网系统模型的求解。
4.1 人工蜂群算法
人工蜂群算法是为了解决多变量函数优化问题而产生的, 来源于蜂群的采蜜行为, 特点是操作简单、全局搜索性高[14]。该算法主要包括以下3个过程。
4.1.1 采蜜蜂寻找新的蜜源
优化问题的求解过程可以看作在D维空间的搜索过程。每个蜜源的位置代表问题的一个可能解。采蜜蜂和蜜源是一一对应的关系, 与第i个蜜源相对应的采蜜蜂根据以下公式寻找新的蜜源。
| $ x^{\prime}{}_{i d}=x_{i d}+\phi_{i d}\left(x_{i d}-x_{k d}\right) $ | (13) |
式中: xid——第i个蜜源第d个变量的值;
i, k∈{1, 2, 3, …, N}, 且i与随机数k互斥, N为蜜源的个数;
d∈{1, 2, 3, …, D}, D为变量个数;
ϕid——随机数, ϕid∈[-1, 1]。
4.1.2 观察蜂根据采蜜蜂的蜜源寻找新的蜜源
每一个观察蜂根据概率选择一个蜜源, 概率公式为
| $ p_{i}=\frac{F_{i}}{\sum\limits_{j=1}^{N} F_{j}} $ | (14) |
式中: Fi, Fj——可能解的适应值。
对于被选中的蜜源, 观察蜂根据式(12)去搜索新的可能解。
4.1.3 侦察蜂寻找新的蜜源
当所有的采蜜蜂和观察蜂都搜索完整个搜索空间时, 如果一个蜜源的适应值在给定的步骤内没有得到改善, 则丢弃该蜜源, 同时该蜜源对应的采蜜蜂变为侦察蜂, 该侦察蜂通过以下公式继续搜索新的蜜源:
| $ x_{i d}=x_{d}^{\min }+\omega\left(x_{d}^{\max }-x_{d}^{\min }\right) $ | (15) |
式中: ω——随机数, ω∈[-1, 1];
xdmin, xdmax——第d个变量的下限和上限。
4.2 改进的人工蜂群算法
蜜蜂在寻找新的蜜源时, 位置的更新公式决定了其能否快速找到更合适的蜜源。未加改进的人工蜂群算法, 虽具有一定的搜索能力, 但搜寻速度较慢而且容易陷入局部最优。为了解决这一问题, 本文在位置更新公式中引入了全局因子, 以扩大搜寻范围。
| $ x^{\prime}{}_{i d}=x_{i d}+\phi_{i d}\left(x_{m d}-x_{k d}\right)+\varphi\left(x_{\text {best }, d}-x_{i d}\right) $ | (16) |
式中: m——随机数, 与i互斥, m∈{1, 2, 3, …, N};
φ——影响因子, φ∈[0, 1];
xbest, d——整个蜜源里丰富度最高的蜜源。
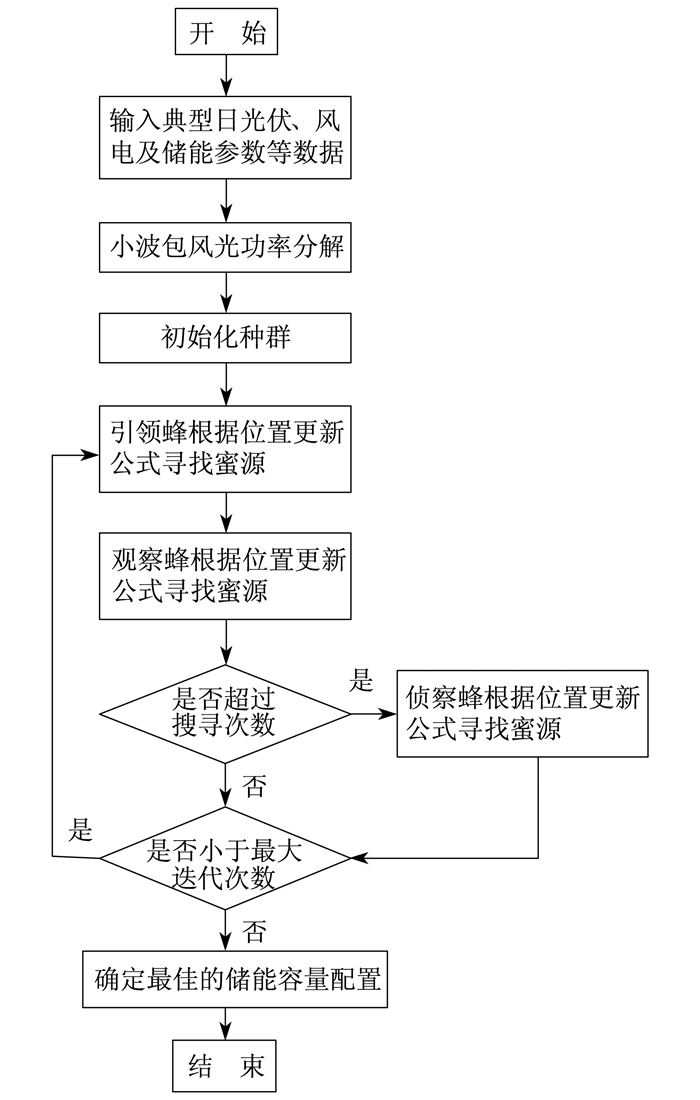
未改进的人工蜂群算法中, 蜜蜂是按照(xid-xkd)的矢量方向进行搜索, 因此引领蜂只能找到自身的历史最优位置和当前位置的蜜源, 在寻找过程中缺乏全局性。本文利用不同蜜蜂间信息共享的优势, 在位置更新公式中引入了全局因子(xbest, d-xid), 增强了蜜蜂搜索蜜源的方向性和目的性, 通过影响因子φ的步长来调整当前位置与最佳蜜源位置之间的距离。储能系统的容量优化配置流程如图 3所示。
5 基于熵权法的储能配置评价
在微电网中, 合理的储能配置方案应在保证用户经济性的同时, 使风光能源在较小范围内波动。利用无储能、单一储能及混合储能3种方案, 对本文所建立的多目标储能容量优化配置模型进行评价。
在应用于不同决策过程的评价时, 熵是一个理想的评价尺度[15]。对于有m个评价指标, n个评价对象的评估问题, 在只有判断矩阵而没有专家权重的情况下, 采用熵权法较为合适。其主要过程如下。
步骤1 数据标准化。采用前文所述的3个评价指标(f1, f2, f3)来评价储能容量的配置。由于不同指标的量纲和数量级存在差异, 因此首先将3个评价指标值进行标准化, 公式为
| $ Y_{i j}=\frac{\max \left(X_{i},:\right)-X_{i j}}{\max \left(X_{i},:\right)-\min \left(X_{i},:\right)} $ | (17) |
式中: X, Y——标准化前后的评价指标值;
i——评价指标, i∈{1, 2, 3};
j——储能的配置方案, j∈{1, 2, 3}。
步骤2 计算各指标的熵矩阵Eij。
步骤3 对标准化后的指标矩阵加熵权规格化后得到矩阵B。
步骤4 求得理想点pi*。
步骤5 计算被评对象到理想点的距离dj*。
步骤6 计算被评对象与理想点的贴近度Tj, 根据Tj对所选方案进行排序。Tj越小, 则方案越好; 若Tj相同, 则用dj*区分, 低值为优。
6 算例仿真与分析
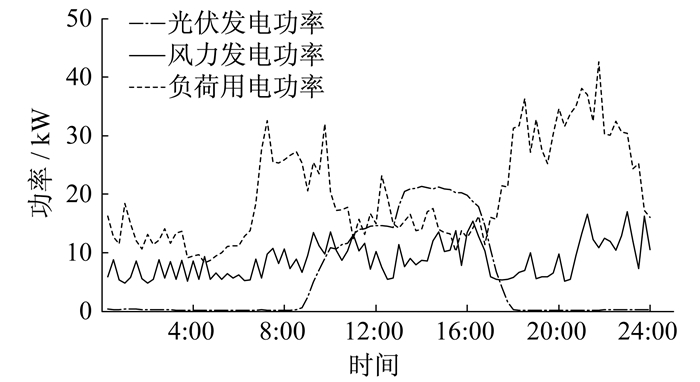
以某并网式微电网作为研究案例, 选取其典型日的光伏和风电数据, 采样周期为15 min, 风力发电的额定输出功率为22 kW, 光伏发电的额定输出功率为18 kW。典型日的光伏、风力发电功率及负荷用电功率如图 4所示。储能系统中蓄电池和超级电容的参数如表 1所示。
表 1
储能系统的相关参数
| 性能参数 | 蓄电池 | 超级电容 |
| 功率成本系数/(元·kW-1) | 2 700 | 1 500 |
| 容量成本系数/(元·kWh-1) | 4 500 | 27 000 |
| 运行维护系数/(元·kW-1) | 155 | 155 |
| 充放电效率/% | 90 | 95 |
| 荷电状态/% | 20~80 | 10~90 |
储能设备分为功率型和能量型两种。能量型电池容量大, 应避免频繁充放电, 以延长寿命时长; 而功率型电池成本高, 应配置小容量, 但允许充放电频率高。在配置微电网的储能系统时, 可用单蓄电池作为能源的调度, 承担风光功率波动的低频分量, 以提高经济性; 用超级电容来承担高频分量, 以满足用电需求。
根据不同的储能系统, 即无储能、蓄电池、混合储能(蓄电池/超级电容)建立多目标函数模型, 利用粒子群算法、人工蜂群算法及改进的人工蜂群算法分别对微电网系统模型进行优化求解, 并对优化结果进行对比分析, 如表 2、表 3和表 4所示。
表 2
粒子群算法对不同储能方案的寻优结果
| 储能方案 | 额定功率/ kW | 额定容量/ kWh | 每日的经济费用/元 | 波动系数 | 能量损失/ kWh |
| 无储能 | 0 | 0 | 382.4 | 0 | 0 |
| 蓄电池 | 31.5 | 63.0 | 300.5 | 0.76 | 16.0 |
| 混合储能 | 31.7/6.0 | 69.1/2.5 | 330.8 | 0.08 | 21.3 |
表 3
人工蜂群算法对不同储能方案的寻优结果
| 储能方案 | 额定功率/kW | 额定容量/kWh | 每日的经济费用/元 | 波动系数 | 能量损失/kWh |
| 无储能 | 0 | 0 | 382.4 | 0 | 0 |
| 蓄电池 | 30.6 | 61.2 | 297.8 | 0.76 | 15.7 |
| 混合储能 | 30.6/5.9 | 66.8/2.5 | 325.4 | 0.08 | 20.7 |
表 4
改进人工蜂群算法对不同储能方案的寻优结果
| 储能方案 | 额定功率/ kW | 额定容量/ kWh | 每日的经济费用/元 | 波动系数 | 能量损失/ kWh |
| 无储能 | 0 | 0 | 382.4 | 0 | 0 |
| 蓄电池 | 30.4 | 60.8 | 293.5 | 0.76 | 15.4 |
| 混合储能 | 30.0/5.9 | 65.7/2.5 | 322.4 | 0.08 | 20.4 |
由表 2至表 4可以看出, 3种算法都能在约束条件范围内找到目标函数的最优值。对于蓄电池的单一储能容量配置, 改进的人工蜂群算法能够得到最少的储能配置, 相对人工蜂群算法每日节省了4.3元, 较粒子群算法节省了7.0元; 从平抑风光波动来看, 3种算法的结果没有区别; 对于储能的能量损失, 改进的人工蜂群算法比人工蜂群算法每日少损失0.3 kWh, 较粒子群算法每日少损失0.6 kWh。
对于蓄电池和超级电容组合的混合储能容量配置, 改进的人工蜂群算法也能得到相对较小的容量配置。对于每日的经济费用, 改进的人工蜂群算法比人工蜂群算法节省了3.0元, 较粒子群算法节省了8.4元; 从平抑风光波动来看, 3种算法的波动系数均相同; 对于能量损失来说, 改进的人工蜂群算法比人工蜂群算法每日减少0.3 kWh, 比粒子群算法每日减少0.9 kWh。综合各项指标数据, 在本文模型求解中, 改进的人工蜂群算法优于其他两种算法。
根据所提算法求解得出3种配置方案, 利用熵权法找出合适的方案, 并计算得出熵权为H=[0.613 7, 0.629 5, 0.451 5], 将熵权加入到属性矩阵中, 得到加权后的规格化矩阵为
| $ \boldsymbol{B}=\left[\begin{array}{cccc} 0 & 0.613\ 7 & 0.414\ 2 \\ 0.629\ 5 & 0 & 0.563\ 3 \\ 0.451\ 5 & 0.110\ 7 & 0 \end{array}\right] $ |
最后, 计算出3种方案到理想点的距离和贴近度的优先顺序, 如表 5所示。
表 5
3种方案到理想点的距离和贴近度优先顺序
| 方案 | 贴近度 | 贴近度优先顺序 | 距离 | 距离优先顺序 |
| 无储能 | 0.385 6 | 2 | 0.125 5 | 2 |
| 蓄电池 | 0.563 3 | 3 | 0.170 8 | 3 |
| 混合储能 | 0.376 7 | 1 | 0.082 7 | 1 |
由表 5可以看出, 应选择蓄电池和超级电容组合的混合储能作为微电网的储能配置方案。蓄电池和超级电容额定功率分别为30.0 kW和5.9 kW, 额定容量为65.7 kWh和2.5 kWh, 每日用户承担的费用为322.4元, 风光能源的波动系数为0.08, 每日的储能能量损失为20.4 kWh。
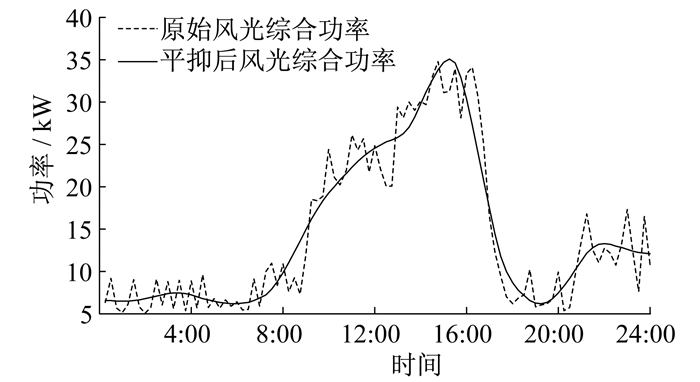
平抑前后风光功率波动对比如图 5所示。可以看出, 平抑后风光波动性得到了较大的改善。
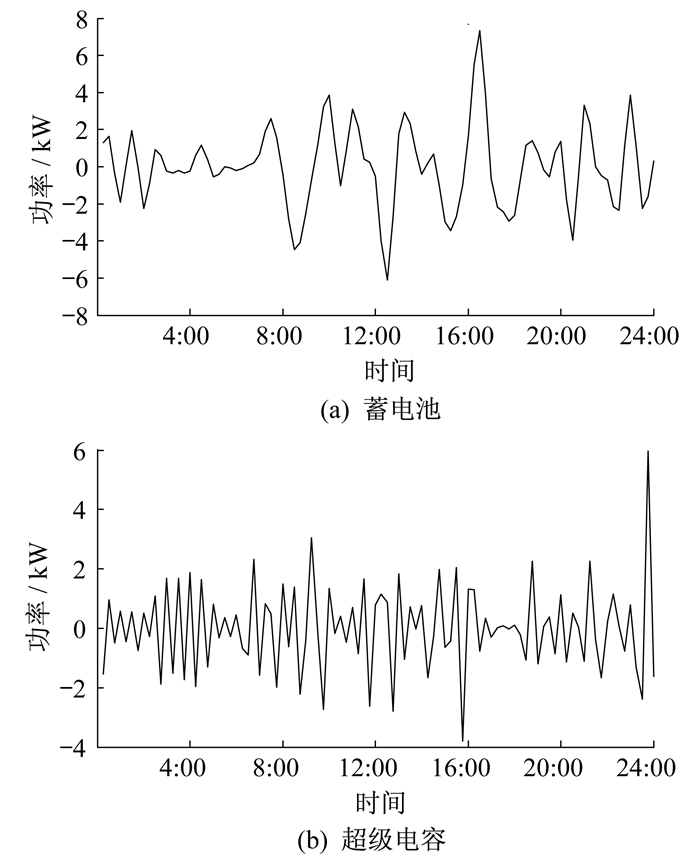
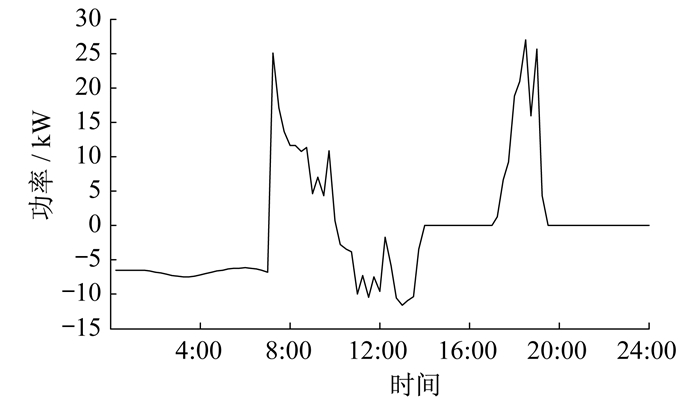
蓄电池储能承担了频率相对较低、波动较小的功率, 而超级电容承担了频率相对较高、波动较大的功率。二者在平抑风光功率中的充放电功率如图 6所示。另外, 蓄电池还承担了风光功率调度过程, 减小了每日需承担的费用, 如图 7所示。
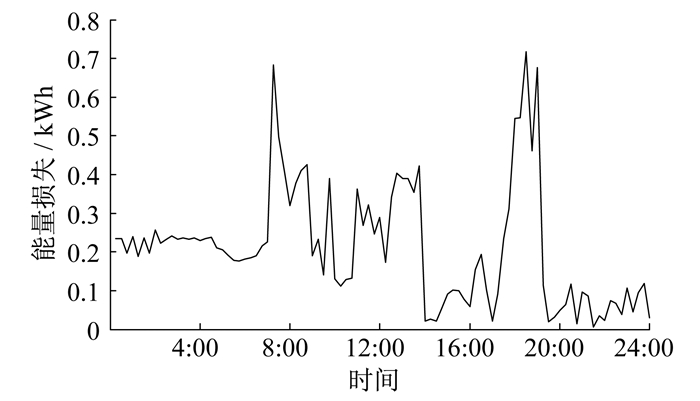
由图 7可以看出, 在用户负荷较大的时段, 蓄电池多以放电为主, 减少了用户每日的购电费用和储能损失量。储能系统每日的能量损失如图 8所示。
7 结论
本文建立了以用户每日承担的费用最小、储能的能量损失最小以及风光能源波动性最小为目标的模型, 用改进的人工蜂群算法对模型进行求解, 并利用熵权法在无储能、单一储能及混合储能3种方案中选择最佳方案。最后, 利用并网性微电网算例验证了此模型的有效性。研究结果表明:
(1) 对于多目标函数模型及多方案决策问题, 通过熵权法可以确定蓄电池和超级电容组合适合作为微电网储能系统。
(2) 在配置微电网的混合储能容量时, 改进的人工蜂群算法相对其他两种算法更易跳出局部最优, 找到最优容量配置。
参考文献
-
[1]张子恒, 吴定会, 杨朝辉, 等. 微电网经济优化运行的综述[J]. 智慧工厂, 2019(11): 50-54.
-
[2]丁明, 陈忠, 苏建徽, 等. 可再生能源发电中的电池储能系统综述[J]. 电力系统自动化, 2013, 37(1): 19-25.
-
[3]胡荣, 岳美. 储能系统在配电网中的优化配置研究[J]. 上海电力学院学报, 2015, 31(3): 223-226.
-
[4]靳雯皓, 刘继春, 刘俊勇. 基于复合储能系统的微网联络线功率优化[J]. 电力自动化设备, 2018, 38(6): 22-28.
-
[5]张国平, 王维俊, 毛龙波, 等. 微电网经济运行优化方法研究综述[J]. 电力与能源, 2019, 40(5): 585-590.
-
[6]肖峻, 张泽群, 张磐, 等. 用于优化微网联络线功率的混合储能容量优化方法[J]. 电力系统自动化, 2014, 38(12): 19-26.
-
[7]李玲玲, 王鑫, 郎永波, 等. 基于改进鲸鱼算法的微网复合储能系统容量优化配置[J]. 电测与仪表, 2019, 56(16): 104-110.
-
[8]陈科彬, 邱晓燕, 史光耀, 等. 基于滑动平均与小波包分解的混合储能容量优化[J]. 电测与仪表, 2018, 55(7): 62-65.
-
[9]武志锴, 许言路, 蒋理, 等. 基于离散傅里叶变换的微电网混合储能容量优化[J]. 华北电力大学学报(自然科学版), 2018, 45(2): 32-38.
-
[10]张晴. 平抑风电波动的混合储能容量配置和经济性评估[D]. 长沙: 湖南大学, 2017.
-
[11]卢芸, 徐骏. 基于小波包分解的风电混合储能容量配置方法[J]. 电力系统保护与控制, 2016, 44(11): 149-54.
-
[12]HAN X, ZHAO S, WEI Z, et al. Planning and overall economic evaluation of photovoltaic-energy storage station based on game theory and analytic hierarchy process[J]. IEEE Access, 2019, 7: 72-81.
-
[13]曹瑛, 刘建锋, 范梦琪, 等. 基于非合作博弈的布谷鸟搜索算法在微电网多目标优化中的应用[J]. 上海电力学院学报, 2018, 34(6): 531-536.
-
[14]李佳华, 马连博, 王兴伟, 等. 基于多目标蜂群进化优化的微电网能量调度方法[J]. 郑州大学学报(工学版), 2018, 39(6): 50-58.
-
[15]刘智, 端木京顺, 王强, 等. 基于熵权多目标决策的方案评估方法研究[J]. 数学的实践与认识, 2005(10): 116-121.