|
|
|
发布时间: 2021-10-28 |
智能电网技术 |
|
|
|
收稿日期: 2020-02-28
中图法分类号: TM715
文献标识码: A
文章编号: 2096-8299(2021)05-0453-06
|
摘要
为了提高短期负荷预测的精度,综合分析了气象、日期等因素,并计算各特征与被预测负荷之间的相关系数,根据各特征与负荷之间的相关性,提出了一种将预测日前几天的负荷作为新特征进行负荷预测的方法。为了验证算法的普适性,采用支持向量回归、随机森林和梯度提升决策树3种机器学习算法,在2016-2018年我国北方某地的真实电力负荷和欧洲智能技术网络(EUNITE)竞赛负荷预测样本数据两个数据集上进行验证,并将预测结果与采用传统特征的算法进行了对比。预测结果显示,相较于传统方法,采用新特征后的短期负荷预测具有更高的预测精度。
关键词
负荷预测; 新特征; 相关系数; 机器学习
Abstract
In order to improve the accuracy of short-term load forecasting, the weather, date and other factors are comprehensively analyzed, and the correlation coefficient between each feature and the predicted load is calculated.According to the correlation between each feature and load, a method of load forecasting is proposed with the load of the days before the forecast as a new feature.In order to verify the universality of the algorithm, three machine learning algorithms, support vector regression, random forest and gradient boosting decision tree, are used to verify on two data sets of the real power load of a certain place in northern China from 2016 to 2018 and the sample data of European Intelligent Technology Network (EUNITE) competition load forecast, and the prediction results are compared with the algorithm using traditional features.The forecast results show that compared with traditional methods short-term load forecasting with new features has higher forecast accuracy.
Key words
load prediction; new features; correlation coefficient; machine learning
电力负荷短期预测的目标是对未来几小时至几天的用电量进行预测。精确的预测结果是电力部门有效部署资源并确保电网安全、降低发电成本、提高经济效益和社会效益的基础。近年来, 随着电力行业市场化改革的推进, 以及智能电网技术的广泛运用, 电网的规模和信息化程度不断扩大。智能量测设备的大量投入有效地提高了对负荷的采集频率以及采集的准确率。这为使用深度学习进行电力负荷预测提供了大数据基础。
对于电力负荷短期预测的研究, 国内外学者已经取得了大量的研究成果。根据电力负荷的时序性和非线性的特点, 对电力负荷预测的方法大致分为两类: 一类是基于统计模型的预测方法, 例如回归分析法[1]、卡尔曼滤波法[2]、指数平均模型法[3]等; 另一类则是机器学习分析方法, 例如支持向量机(Support Vector Machines, SVM)算法[4]、随机森林(Random Forest, RF)算法[5]、神经网络算法[6]等。这些算法大都采用日期、温度、天气以及日期类型等变量作为特征进行电力负荷预测。对于负荷趋势而言, 有些用户的负荷曲线并没有呈现明显的时间周期性规律, 考虑到负荷曲线本身在短时间内是一个连续变化的曲线, 并不会发生突变, 因此本文提出了一种采用预测日前几日的负荷数据作为新特征替换年、月、日这些日期特征的新方法对电力负荷进行预测, 并运用不同算法在真实用电数据上进行验证。
1 负荷影响因素
传统的负荷预测方法将影响短期负荷的因素归纳为历史负荷数据、气候因素和日期类型3类。文献[7]提出的电力负荷公式为
| $ L(t)=L_{\mathrm{n}}(t)+L_{\mathrm{w}}(t)+L_{\mathrm{s}}(t)+L_{\mathrm{r}}(t) $ | (1) |
式中: L(t)——t时刻的实际负荷;
Ln(t)——t时刻的趋势负荷, 其应该满足高斯分布;
Lw(t)——t时刻的气象因素(如温度、湿度等)对此刻负荷的影响;
Ls(t)——t时刻一些特殊事件(如节假日、检修等)所带来的负荷波动;
Lr(t)——t时刻负荷的随机波动, 可以将其看作负荷的噪声, 如突发事故等, 因此常常被忽略。
文献[5]通过提高Lw(t)和Ls(t)的预测精度来提高t时刻电力负荷整体的预测精度。短期电力负荷的预测结果受到很多外界因素的影响, 常见的因素有气候因素, 如温度的高低、湿度的大小、天气类型(晴天/下雨/多云)以及风速的大小都会对负荷产生影响, 因此获取准确的天气信息会提高对Lw(t)预测的精确度。日期类型也是影响预测精度的另一个重要因素, 日期类型分为工作日和非工作日, 非工作日又可分为普通周六、周日和节假日, 如五一、春节等, 因此合理利用这些日期类型因素可以提高Ls(t)预测的精确度。
2 历史负荷数据分析
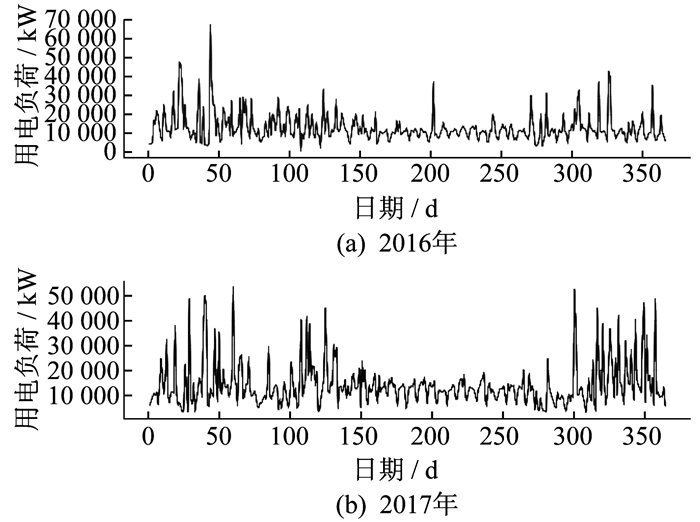
由于某些地区或用户的用电负荷时序性较差, 如北方某地区2016年和2017年的年负荷曲线如图 1所示。
由图 1可以看出, 用电年负荷曲线并没有明显的时间规律, 考虑到几天内的用电数据之间有明显相关性, 因此本文通过计算预测日实际负荷与前几天负荷数据之间的相关系数, 并将年、月、日3个变量与预测日负荷之间的相关系数进行对比, 来选取与预测日用电量相关系数较大的变量作为特征进行负荷预测。为了保证相关系数计算的准确性, 使用Pearson相关系数、Kendall相关系数和Spearman相关系数3种计算方法, 分别计算各特征与预测日负荷数据之间的相关性。计算结果见表 1和表 2所示。表 1中, B-day1, B-day2, B-day3, B-week分别表示预测日前1日、前2日、前3日和前7日的负荷数据。
表 1
历史负荷与预测日负荷的相关系数
| 计算方法 | 相关系数 | |||
| B-day1 | B-day2 | B-day3 | B-week | |
| Pearson | 0.228 | 0.024 | 0.013 | 0.064 |
| Kendall | 0.191 | -0.009 | 0.003 | 0.167 |
| Spearman | 0.267 | -0.013 | 0.006 | 0.230 |
表 2
日期特征与预测日负荷的相关系数
| 计算方法 | 相关系数 | ||
| 年 | 月 | 日 | |
| Pearson | 0.063 | -0.079 | 0.046 |
| Kendall | 0.063 | -0.056 | 0.035 |
| Spearman | 0.077 | -0.071 | 0.052 |
对比发现, 预测日前1日和前7日的负荷数据与预测日负荷的相关系数要大于年、月、日与预测日负荷的相关系数。因此, 本文提出选取预测日前1日和前7日的负荷数据作为新特征代替经典方法中的日期特征来进行短期负荷预测。
3 机器学习算法
3.1 支持向量回归算法
支持向量回归(Support Vector Regression, SVR)算法作为SVM算法的一种推广, 应用广泛。算法原理为构造一个决策平面, 通过计算样本点到决策平面的距离来进行回归预测。决策超平面由wT和b来确定: wT为法向量或权重, 决定了超平面的方向; b为位移项, 决定了超平面与原点之间的距离。假设给样本集为{(x1, y1), (x2, y2), (x3, y3), …, (xn, yn)}, 其中x1, x2, x3, …, xn为影响因素, 例如日期类型、湿度等; y1, y2, y3, …, yn为所对应日负荷数据。决策超平面公式可表示为
| $ f(\boldsymbol{x})=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b $ | (2) |
样本点距离决策超平面距离公式为
| $ \begin{gathered} y_{i}-f(\boldsymbol{x})=y_{i}-\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}-b<\varepsilon \\ i=1,2,3, \cdots, n \end{gathered} $ | (3) |
SVR通过计算各个样本点到决策超平面的距离来找到一个最优超平面, 使得决策超平面两侧距离超平面最近的样本点距离最远, 目标函数即满足
| $ \max \limits_{\boldsymbol{w}, b}\left\{\frac{1}{\|\boldsymbol{w}\|} \min \limits_{i}\left[y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{\phi}\left(x_{i}\right)+b\right)\right]\right\} $ | (4) |
式中: ϕ(xi)——将xi映射后的特征向量。
由于有些数据集是线性不可分的, 为了解决线性不可分问题, 同时为了防止过拟合现象, 所以本文引入惩罚因子C和松弛因子ξi两个超参数。此时目标函数变为
| $ \min \limits_{\boldsymbol{w}, b} \frac{1}{2}\|\boldsymbol{w}\|^{2}+C \sum\limits_{i=1}^{n} \xi_{i} $ | (5) |
约束条件为
| $ \left\{\begin{array}{l} y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \emptyset\left(\boldsymbol{x}_{i}\right)+b\right) \geqslant 1-\xi_{i} \\ C \geqslant 0 \\ \xi_{i} \geqslant 0, i=1,2,3, \cdots, n \end{array}\right. $ | (6) |
为了求解目标函数同时满足式(6)的约束条件, 应用拉格朗日函数, 并将此问题转化为其对偶问题进行求解。由于一些样本点在低维空间线性不可分, 因此引入核函数将其映射到高维空间分开。常用核函数有Sigmoid核函数、高斯核函数、多项式核函数等。最终求得wT和b以及选择的核函数来确定超平面。
3.2 随机森林算法
RF算法由于其在噪声以及异常值方面有很好的包容性, 且在回归预测中不易出现过拟合, 因此该算法在回归、分类方面均有较好的应用, 适用于负荷预测。RF算法原理为, 将若干的分类性能一般的决策树通过某种规则组合到一起, 形成一个分类、回归效果较好的“森林”, 通过森林中所有树投票来决定预测结果, 从而提高预测精度。
RF是K个分类与回归树(Classification And Regression Tree, CART)的集合, 数据集中有N个样本, M个特征变量(如日期类型、温度等)。利用Booststrap Sample方法抽取K次, 每次有放回地从原始数据中抽取N个样本, 最终获得K个样本数量为N的样本集。从M个特征变量中随机选取m个特征变量构成一个特征变量子集。m为一个定值, 通过最小二乘偏差函数来选择最优特征进行分裂, 从而形成K个决策树。由于每一棵CART树分裂都是随机的, 正好避免了过拟合的产生。多个CART树形成随机森林, 当输入一个样本时, 每一棵决策树都会进行判断, 产生一个预测值, 将这些值进行加权平均计算, 所得结果为最终的预测结果。
3.3 梯度提升决策树算法
梯度提升决策树(Gradient Boosting Decision Tree, GBDT)算法是由梯度提升机和决策树的结合改进算法。当梯度提升机的基函数选择决策树时便成为梯度提升决策树算法。它的基本原理是在损失函数的负梯度方向上搭建若干决策树, 将这些决策树组合成一个强回归决策树。这便是最终的回归预测模型。
训练集表示为{(x1, y1), (x2, y2), (x3, y3), …, (xm, ym)}。x=[x1, x2, x3, …, xn]为模型的输入向量, 包含历史负荷、气象因素、日期类型等特征。若上一次迭代得到的决策树的损失函数为L[y, ft-1(x)], 其中y为负荷真实值, ft-1(x)为上一次迭代的决策树模型, 则本次损失函数的负梯度为
| $ r_{t i}=\frac{\partial L\left[y_{i}, f\left(x_{i}\right)\right]}{\partial f\left(x_{i}\right)} $ | (7) |
其中, f(x)=ft-1(x)。
本次损失函数为
| $ L\left[y_{i}, f\left(x_{i}\right)\right]=L\left[y, f_{t-1}(\boldsymbol{x})\right]+h_{t}(\boldsymbol{x}) $ | (8) |
式中: ht(x)——本次要寻找的弱回归树。
对于每个叶子节点中的样本, 找到使损失函数最小, 即拟合叶子节点最优的预测值Ctj, 公式为
| $ C_{t j}=\arg \min \sum\limits_{i=1}^{n} L\left[y, f_{t-1}(\boldsymbol{x})+c\right] $ | (9) |
式中: j——第t棵弱决策树的叶子节点个数, j=1, 2, 3, …, k;
c——采用线性索引方法找到使所有区域损失函数最小的最优常数。
最终得到的本次强回归决策树的表达式为
| $ f(\boldsymbol{x})=f_{t-1}(\boldsymbol{x})+\sum\limits_{j=1}^{k} C_{t j} \boldsymbol{I} $ | (10) |
式中: I——单位阵。
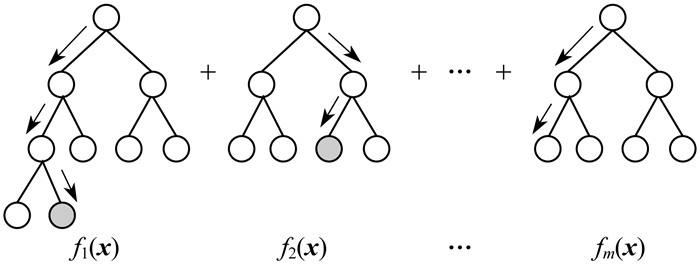
梯度提升决策树的最终预测模型为
| $ F(\boldsymbol{x})=f_{0}+f_{1}(\boldsymbol{x})+\cdots+f_{m}(\boldsymbol{x}) $ | (11) |
式中: fi(x)——决策树i的预测结果, i=1, 2, 3, …, n。
梯度提升决策树模型如图 2所示。
4 算例分析
4.1 确定所用数据
本文所用数据为北方某地区的电力负荷数据。原数据中包含了2016年1月1日至2018年5月31日共29个月的真实电力负荷数据和气象数据, 负荷数据的采集频率为一日一次, 气象数据包括最低温度、最高温度、最低湿度、最高湿度。
选择2016年1月1日至2017年12月31日的负荷数据和气候数据作为训练数据, 选择2018年1月1日至2018年5月31日的负荷数据为预测数据。最终确定: 输入变量为预测日前1日和前7日的负荷数据; 气候数据为每日最低气温、最高气温、最低湿度、最高湿度; 日期变量包括星期变量, 分别为星期一到星期日, 以及是否为工作日、是否为节假日等日期类型变量。每一日的数据为一条样本, 每条样本共有11个输入变量。
为了体现本文所提方法的通用性, 增加一组负荷数据进行验证。该数据为欧洲智能技术网络(EUNITE)竞赛负荷预测样本数据, 数据包括了1997年、1998年斯洛伐克东部电力公司某电厂的真实负荷数据, 以及1997年、1998年每年的节假日数据和每日的天气数据。本文采用1997年1月1日到1998年8月31日的数据作为训练集, 预测1998年9月1日到12月31日的用电负荷, 其中输入变量为预测日前1日和前7日的负荷数据; 气候数据为每日温度; 日期变量包括星期变量, 分别为星期一到星期日, 以及是否为工作日、是否为节假日等。每一日的数据为一条样本, 每条样本共有7个输入变量。
4.2 数据预处理
4.2.1 异常数据处理
在原始数据中由于信息传递过程中可能产生错误, 所以导致一些异常值的出现, 而且出现了少量的数据丢失。这些丢失或异常的数据会影响预测的准确度, 应该首先予以处理。采用文献[8]提出的解析分析法以及修正法来搜索异常数据和补充缺少的数据。
4.2.2 数据归一化
由于各输入数据的量纲不同, 各特征向量之间数值差距过大, 会影响最后整体的预测结果, 因此对输入数据先进行归一化处理。归一化后使各特征向量的数据限制在[0, 1]。归一化的公式为
| $ x^{*}=\frac{x-x_{\min }}{x_{\max }-x_{\min }} $ | (12) |
式中: x*——归一化后的数值;
x——需要归一化的数据;
xmin, xmax——该数据里的最小值和最大值。
4.2.3 评价指标
为了评估模型预测的性能, 设置平均绝对百分误差yMAPE和平均预测精度yFA.avg2项指标。计算公式分别为
| $ y_{\mathrm{MAPE}}=\frac{1}{n} \sum\limits_{i=1}^{n}\left|\frac{x_{\mathrm{act}}(i)-x_{\mathrm{pre}}(i)}{x_{\mathrm{act}}(i)}\right| $ | (13) |
| $ y_{\mathrm{FA}}=\left[1-\frac{\left|x_{\mathrm{act}}(i)-x_{\mathrm{pre}}(i)\right|}{x_{\mathrm{act}}(i)}\right] \times 100 \% $ | (14) |
| $ y_{\mathrm{FA} . \mathrm{avg}}=\frac{1}{n} \sum\limits_{i=1}^{n} y_{\mathrm{FA}}(i) $ | (15) |
式中: n——预测天数;
xact(i), xpre(i)——第i天负荷的真实值和预测值。
4.3 实验结果分析
将数据进行预处理后, 分别使用SVR, RF, GBDT 3种算法对本文所提出的新特征进行负荷预测, 并与采用年、月、日作为日期特征的传统方法进行对比。我国北方某地区的电力负荷预测结果对比如表 3所示。
表 3
预测结果对比
| 算法 | 原始特征 | 新特征 | |||
| yMAPE | yFA.avg | yMAPE | yFA.avg | ||
| SVR | 0.028 | 97.2 | 0.020 | 98.0 | |
| RF | 0.009 | 99.1 | 0.007 | 99.3 | |
| GBDT | 0.025 | 97.5 | 0.022 | 97.8 | |
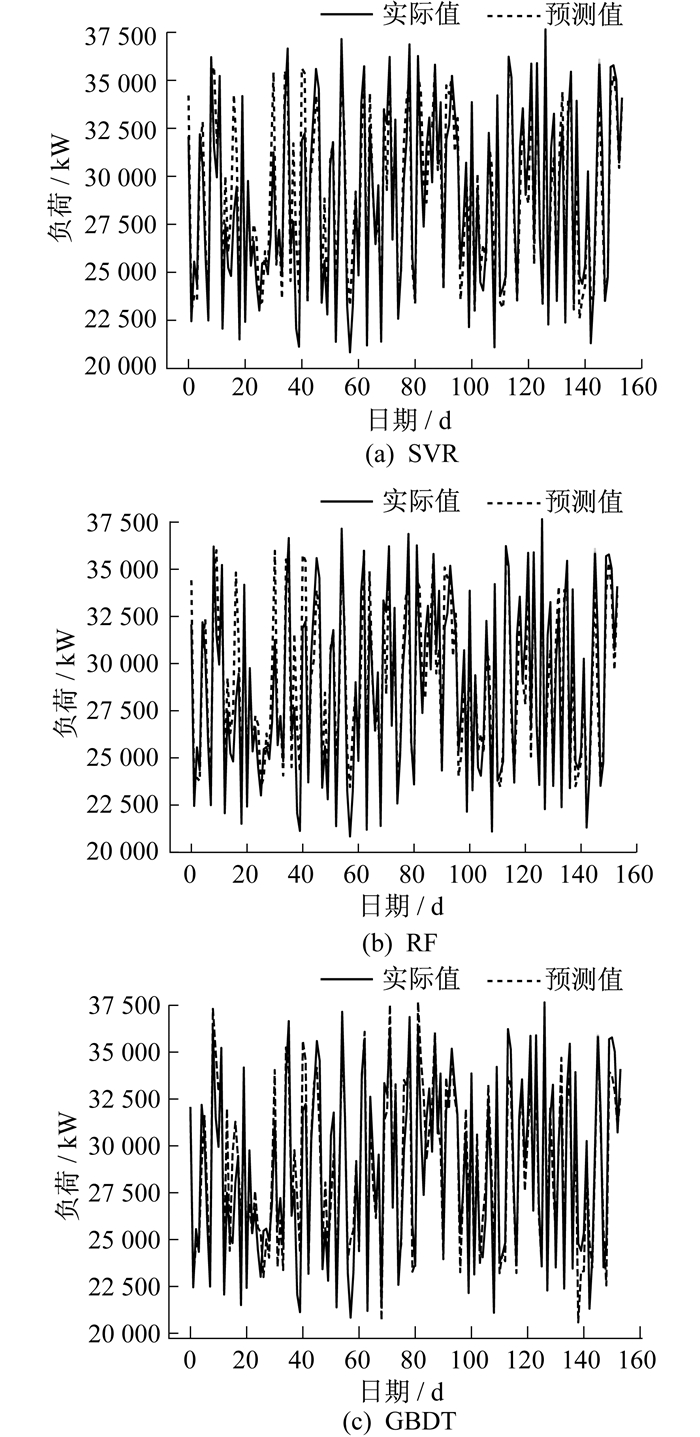
图 3为使用新特征后3种不同算法的实际值与预测值的折线图。由图 3可知: SVR, RF, GBDT这3种算法的平均预测精度分别为98.0%, 99.3%, 97.8%, 相对于传统算法, 绝对百分误差分别下降了28.57%, 22.22%, 12.00%。整体来看, 预测值大部分与实际值接近或重合, 且没有出现个别点误差很大的情况, 表明本文提出方法能够较为准确地对负荷进行预测。
斯洛伐克东部某电厂的电力负荷预测结果对比如表 4所示。
表 4
斯洛伐克东部某电厂的电力负荷预测结果对比
| 算法 | 原始特征 | 新特征 | |||
| yMAPE | yFA.avg | yMAPE | yFA.avg | ||
| SVR | 0.039 1 | 96.09 | 0.030 6 | 96.94 | |
| RF | 0.026 7 | 97.33 | 0.022 6 | 97.74 | |
| GBDT | 0.043 6 | 95.64 | 0.038 6 | 96.14 | |
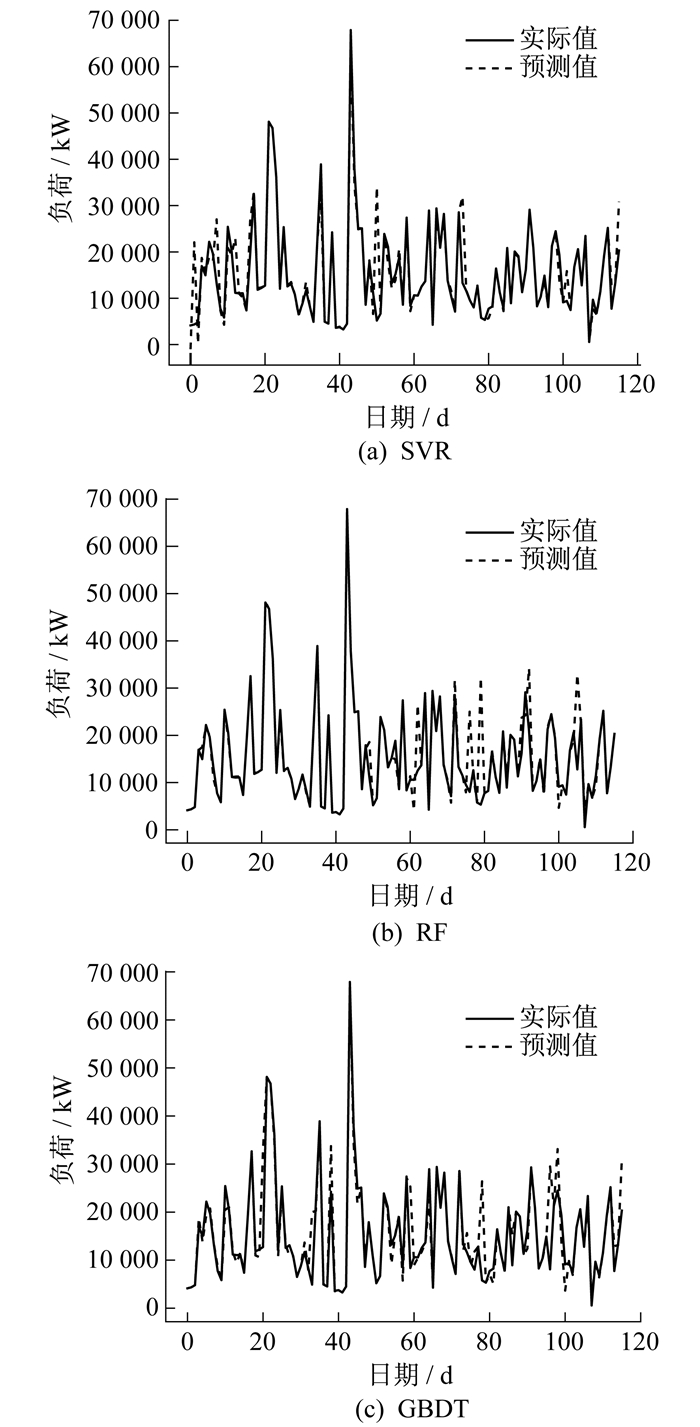
图 4为使用新特征后3种不同算法的实际值与预测值的折线图。由图 4可知: SVR, RF, GBDT 3种算法的平均预测精度分别为96.40%, 97.74%, 96.14%, 相对于传统算法, 绝对百分误差分别下降了21.74%, 15.36%, 11.47%。
通过在2个数据集上进行验证, 表明本文所提出的方法对于电力负荷的变化趋势和局部细节均有较好的预测效果, 相对于传统的方法, 预测误差明显降低, 可以有效地提高预测精度。
5 结语
考虑到负荷曲线并没有明显时间规律, 本文提出了一种使用新特征的短期负荷预测方法。由于负荷本身在短时间内是一个连续变化的曲线, 并不会发生突变, 因此引入前几日的历史负荷数据作为新特征进行负荷预测, 并与现有的负荷预测方法进行了比较。实验结果表明, 本文所提方法能有效地减少预测误差, 提高了预测准确率, 具有一定的实用意义。在今后的工作中, 将会验证该特征运用在其他算法是否有相似结论。
参考文献
-
[1]MAHMUD M A. Isolated area load forecasting using linear regression analysis: practical approach[J]. Energy and Power Engineering, 2011, 3(4): 547-550. DOI:10.4236/epe.2011.34067
-
[2]潘志远, 韩学山. 电网节点负荷的立体化预测方法[J]. 电力系统自动化, 2012, 36(21): 47-52.
-
[3]OSTERAGOVA E, OSTERTAG O. Forecasting using simple exponential smoothing method[J]. Acta Electrotechnica et Informatica, 2012, 12(3): 62-66.
-
[4]钱志. 基于改进型SVR的电网短期负荷预测[J]. 中国电力学报, 2016, 49(8): 54-58.
-
[5]吴潇雨, 和敬涵, 张沛, 等. 基于灰色投影改进随机森林算法的电力系统短期负荷预测[J]. 电力系统自动化, 2015, 39(12): 50-55.
-
[6]陆继翔, 张琪培, 杨志宏, 等. 基于CNN-LSTM混合神经网络模型的短期负荷预测方法[J]. 电力系统自动化学报, 2019, 43(8): 130-137.
-
[7]CHEN H, CANIZARES C A, SINGH A. ANN-based short term load forecasting in electricity markets[C]//2001 IEEE Power Engineering Society Winter Metting. Conference Proceedings. Columbus, OH, USA: IEEE, 2001: 7028214.
-
[8]毕云帆, 张健, 胥晓晖, 等. 基于梯度提升决策树的电力短期负荷预测模型[J]. 青岛大学学报, 2018, 33(3): 70-75.