|
|
|
发布时间: 2021-10-28 |
智能电网技术 |
|
|
|
收稿日期: 2020-07-18
基金项目: 上海绿色能源并网工程技术研究中心资助项目(13DZ2251900)
中图法分类号: TM727
文献标识码: A
文章编号: 2096-8299(2021)05-0459-08
|
摘要
在孤岛运行的低压微电网中,因线路阻抗的不匹配性,导致传统下垂控制无法按照下垂增益精确均分有功功率,各分布式储能单元必然会出现荷电状态(SOC)差异,造成蓄电池过充电或过放电,缩短了储能单元的使用寿命。针对上述问题,提出了一种低压微电网分布式储能系统分级控制策略。首先通过功率平衡级动态调节虚拟阻抗,消除不匹配线路阻抗对有功分配精度的影响;然后,通过SOC平衡级控制,各个储能单元根据其SOC动态调节有功功率,使得SOC误差以e指数曲线下降,最终实现储能单元在放电过程中SOC均衡。采用动态一致性算法,可实现各分布式储能单元的信息共享,提高了系统的可靠性和灵活性。同时,基于小信号理论对所提控制策略进行了稳定性分析,并讨论加速因子对系统稳定性的影响。仿真对比结果验证了所提控制策略的有效性和可行性。
关键词
低压微电网; 下垂控制; 分布式储能单元; 荷电状态均衡
Abstract
In the islanded AC low-voltage micro-grid, the accurate sharing of active power cannot be realized by droop gain of the traditional droop control, which is caused by the unmatched line impedance.Differences of state-of-charge (SOC) will exist inevitably in each distributed energy storage unit (DESU), which leads to overcharge or overdischarge and shorter service life of battery.Therefore, a hierarchical control strategy for distributed energy storage system (DESS) in AC low-voltage microgrids is proposed.The virtual impedance is obtained by the power balancing stage, which eliminates the influence of accurate sharing of active power caused by unmatched impedance.In the stage of SOC balancing, each DESU dynamically adjusts the output active power according to SOC, and SOC deviation decreases with e-index curve, ultimately achieveing SOC balancing of the DESUs during discharging process.The dynamic consensus algorithm is applied for information sharing between the DESUs.It can provide higher system reliability, expandability, and flexibility due to its distributed control architecture.The stability of proposed strategy is analyzed based on small signal theory and the influence of acceleration factor is discussed.The simulation comparison results verify the effectiveness and feasibility of the proposed control strategy.
Key words
low-voltage microgrid; droop control; distributed energy storage unit; state of charge balancing
随着全球能源、环境问题的日益严峻, 微电网受到了世界各国研究者的广泛关注。由分布式电源(Distributed Generation, DG)、储能、负荷、变流器、监控和保护装置有机整合的微电网[1-2], 实现了DG的灵活控制[3]。由于DG的输出功率具有间歇性和随机性特征, 其安全性和可靠性较弱[4], 因此需配置分布式储能系统(Distributed Energy Storage System, DESS)以保障微电网的功率平衡。
在充放电过程中, DESS中各分布式储能单元(Distributed Energy Storage Unit, DESU)的荷电状态(State of Charge, SOC)实时发生变化, 受不匹配线路阻抗的影响, 各DESU的SOC会出现差异, 导致DESU过充放电, 缩短了DESU的使用寿命, 情况严重时甚至会使蓄电池发生过热现象, 发生火灾[5]。为此, 很多研究者提出了解决SOC无法实现均衡的方法。文献[6-7]提出了自适应下垂控制, 利用下垂系数反比于SOC的n次方, 通过实时改变下垂系数, 实现SOC均衡。放电时下垂系数mp正比于1/SOCn, n越大SOC均衡速度越快, 均衡精度越低。文献[8-9]提出利用模糊算法的改进下垂控制, 通过SOC偏差和输出电压偏差实时修改下垂参数, 以实现SOC均衡, 但模糊控制器的模糊规则设计较为复杂, 工程上较难实现。文献[10-11]在交流微电网中, 根据SOC实时变化, 自适应调节各储能单元的下垂系数, 实现负荷功率在各储能单元之间的动态分配和SOC均衡, 但均衡精度较低且缺少足够的算例验证。
上述研究中提出的SOC均衡控制策略均未考虑线路阻抗对负荷分配的影响, 然而在低压交流微电网中, 不匹配的线路阻抗将导致传统下垂控制无法按照下垂增益精确分配有功功率, 势必会造成各储能单元的SOC无法实现均衡, 导致过充过放。文献[12]在低压微电网中设计了新型下垂控制, 利用本地高低脉冲分别实现SOC均衡与电压恢复。由于其控制策略是离散的, 所以暂态输出功率波动较大, 电能质量较低, 甚至会出现频率偏移现象。基于上述分析, 本文提出了一种低压微电网分布式储能系统分级控制策略经MATLAB仿真对比结果验证了所提控制策略能够克服线路阻抗的影响, 实现SOC快速均衡, 且其输出功率平滑、波动小。
1 低压微电网下垂控制理论
1.1 低压微电网结构
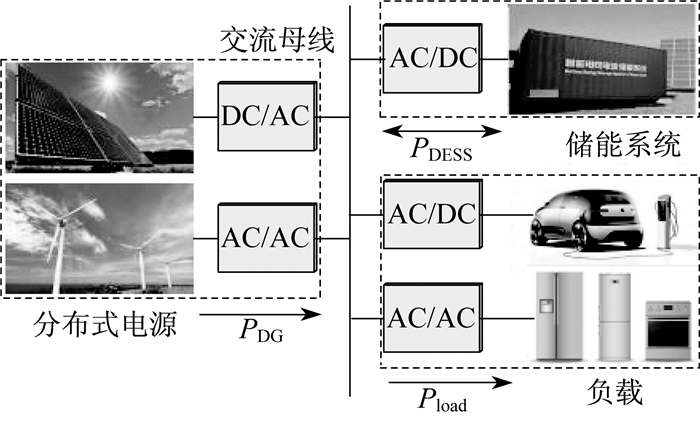
本文研究的孤岛低压微电网结构如图 1所示。DG单元和储能单元通过电压源型逆变器(Voltage Source Inverter, VSI)连接于交流母线公共耦合点(Point of Common Coupling, PCC)。
图 1中: PDG为DG输出的总功率; PDESS为DESS输出的总功率; Pload为负荷总功率。由此, 微电网中的功率平衡表达式为
| $ P_{\mathrm{DESS}}=P_{\text {load }}-P_{\mathrm{DG}} $ | (1) |
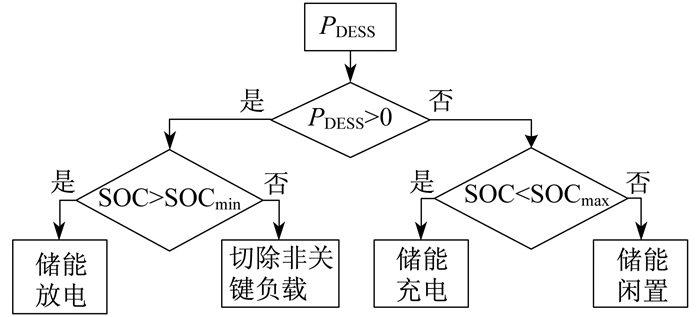
孤岛微电网DESUs工作情况如图 2所示。
孤岛微电网中, 当PDESS≥0且储能单元SOC>SOCmin时, 储能单元放电; 当SOC≤SOCmin时则储能单元进入闲置状态, 根据负荷分类切除非关键负荷; 当PDESS < 0且储能单元SOC < SOCmax时, 储能单元充电; 当SOC≥SOCmax时则储能单元进入闲置状态。本文以储能单元放电为例, 提出了基于下垂控制的SOC均衡方法, 使得DESU在放电过程中SOC趋于均衡, 避免DESU过放电。
1.2 分布式储能单元SOC不均衡分析
为了提高微电网的冗余性和可靠性, 将多组DESU通过VSI并联连接于PCC, 如图 3所示。图 3中: DESUi和DESUj分别为任意2组储能单元; Rlinei和Rlinej分别为相应储能单元到公共耦合点的等效线路阻抗; UPCC为直流母线电压。
在低压微电网中, 系统呈现阻性。由此, 忽略线路阻抗中的感性成分, DESUi输出的有功功率Pi和无功功率Qi分别为
| $ P_{i} =\frac{U_{\mathrm{PCC}}\left(U_{\mathrm{PCC}}-U_{i} \cos \delta_{i}\right)}{R_{i}} $ | (2) |
| $ Q_{i} =-\frac{U_{i} U_{\mathrm{PCC}} \sin \delta_{i}}{R_{i}} $ | (3) |
式中: Ui——DESUi输出电压Ui的幅值;
Ri——线路电阻;
δi——DESUi的输出电压与PCC电压的相角差。
由式(2)和式(3)可知, 在低压微电网中, 分布式储能单元输出的有功功率与电压幅值差成正比, 输出的无功功率与相角差成正比。由此下垂控制的表达式为
| $ \omega_{i} =\omega^{*}-k_{q} Q_{i} $ | (4) |
| $ U_{i} =U^{*}-k_{p} P_{i} $ | (5) |
式中: ωi——DESUi的输出电压角频率;
ω*——参考角频率;
kq——Q-ω下垂系数;
U*——参考电压;
kp——P-U下垂系数。
由于储能单元SOC变换较慢且容量较大, 故忽略充放电过程中直流侧电压的变化, 即图 3中UDC基本不变。ESOC表征的是储能单元当前的输出能力, 可定义为
| $ E_{\mathrm{SOC}, i}=E_{\mathrm{SOC}, i_{-} 0}-\frac{\int i_{\mathrm{DC}\_i} \mathrm{d} t}{C_{\mathrm{e}}} $ | (6) |
式中: ESOC, i——DESUi当前的SOC;
ESOC, i_0——DESUi初始的SOC;
iDC_i——DESUi输出电流;
Ce——储能单元容量。
忽略发变电损耗, 根据能量守恒原理, 则有
| $ P_{i}=P_{\mathrm{DC}\_ i}=U_{\mathrm{DC}} i_{\mathrm{DC}\_ i} $ | (7) |
式中: PDC_i——DESUi输入功率。
结合式(6)和式(7), 可得
| $ E_{\mathrm{SOC}, i}=E_{\mathrm{SOC}, i_{-} 0}-\frac{\int P_{i} \mathrm{~d} t}{U_{\mathrm{DC}} C_{\mathrm{e}}} $ | (8) |
对式(8)进行求导
| $ \dot{E}_{\mathrm{SOC}, i}=-\frac{P_{i}}{U_{\mathrm{DC}} C_{\mathrm{e}}} $ | (9) |
因此, 当系统稳定时, 各储能单元输出的有功功率相等是SOC均衡的必要条件。根据图 3, 各DESUi的等效线路阻抗上的压降ΔUi可近似为
| $ \Delta U_{i} \approx \frac{X_{i} Q_{i}+R_{i} P_{i}}{U^{*}} $ | (10) |
式中: Xi——线路电感。
根据式(10)和图 3的电路关系, 可得
| $ U_{i}=U_{\mathrm{PCC}}+\frac{X_{i} Q_{i}+R_{i} P_{i}}{U^{*}} $ | (11) |
在低压微电网系统中, R≫X, 由此可将式(11)简化为
| $ U_{i}=U_{\mathrm{PCC}}+\frac{R_{i}}{U^{*}} P_{i}=U_{\mathrm{PCC}}+k_{i} P_{i} $ | (12) |
式中: ki——DESUi侧线路阻抗系数。
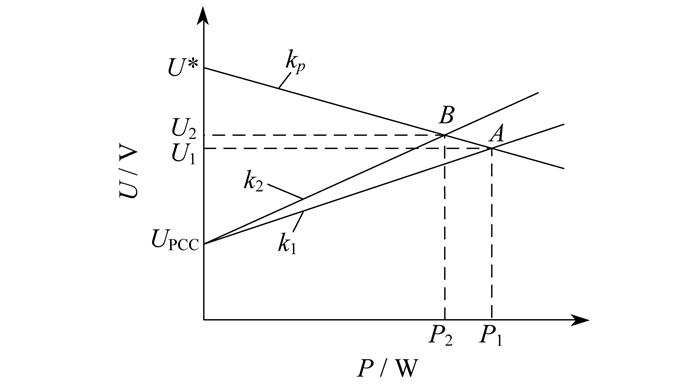
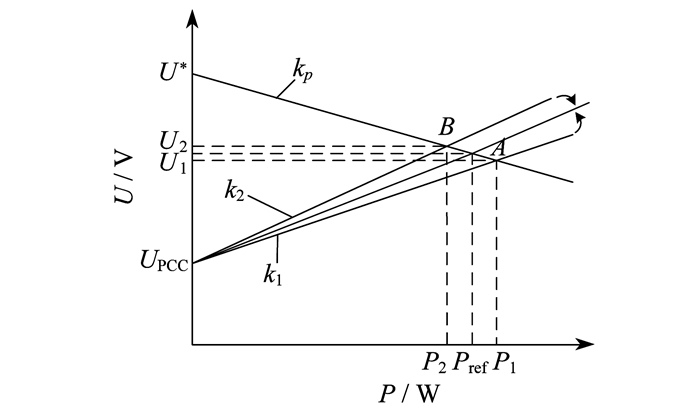
以2台DESU(记为DESU1和DESU2)为例, 根据式(12)可得其有功功率传输特性曲线, 结合下垂控制曲线, 也即式(5), 得到2台DESU的有功分配关系如图 4所示。由图 4可知, 两者的交点A和B为稳态运行点。当不匹配线路阻抗R1 < R2时, 则P1>P2, 2台DESU输出有功功率不均分, SOC无法均衡。
2 分级控制策略分析
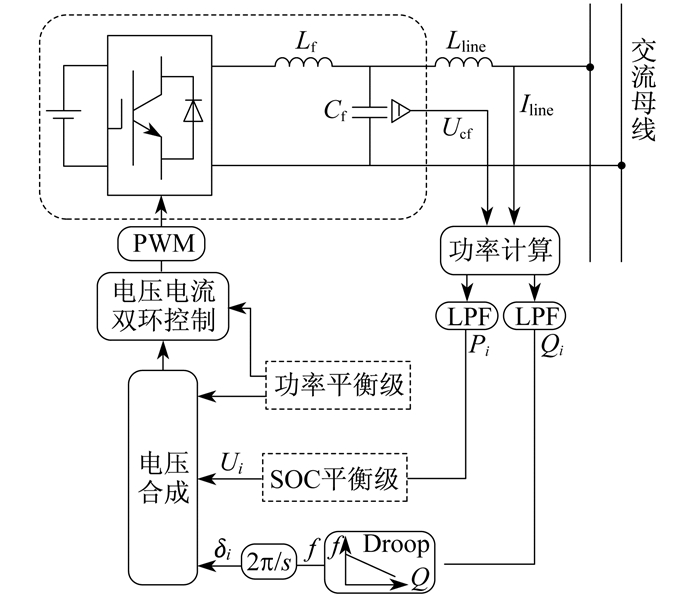
本文提出了一种分级控制策略, 总体控制框图如图 5所示。其中, PWM为脉宽调制, LPF为低通滤波器。
各储能单元通过功率平衡级动态调整虚拟阻抗, 消除不匹配线路阻抗对有功功率分配精度的影响; 随后利用SOC平衡级控制, 根据储能单元的SOC动态调节有功输出, 实现SOC均衡。
2.1 功率平衡级控制
在低压微电网中, 线路阻抗呈阻性, 忽略其感性成分, 即只需满足等效线路电阻与虚拟电阻之和相等[13]即可。
以n台容量相等的DESU并联为例, 其等效输出阻抗关系为
| $ R_{\text {line} i}+\Delta R_{i} =R_{\text {line} j}+\Delta R_{j}=\frac{1}{n} \sum\limits_{k=1}^{n} R_{\text {line}k} $ | (13) |
| $ \Delta R_{i} =\frac{1}{n} \sum\limits_{k=1}^{n} R_{\text {line}k }-R_{\text {line}i } $ | (14) |
式中: ΔRi, ΔRj——DESUi和DESUj的虚拟阻抗。
考虑到微电网中等效线路参数的不确定性, 无法准确得到线路阻抗值, 所以设计了实时动态修改虚拟电阻, 即
| $ \Delta R_{i}=\frac{k_{\mathrm{a}}}{s}\left(P_{i}-P_{\mathrm{ref}}\right) $ | (15) |
式中: ka——积分常数;
Pref——有功功率的平均值。
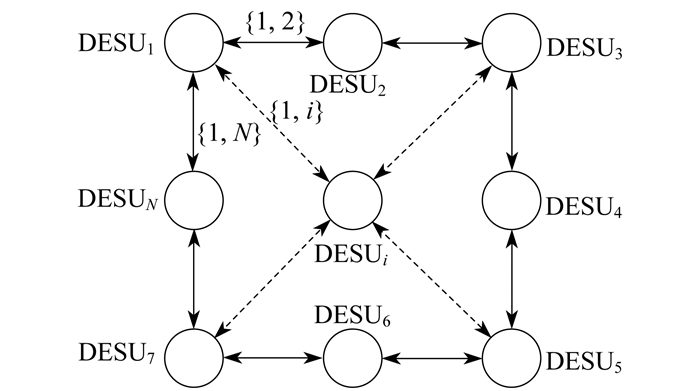
动态一致性算法可用于消除全局通信的依赖, 实现DESU之间的信息共享, 降低通信成本[14]。本文将连接到微电网的储能单元看作一个由N个节点和一系列边E组成的网络, 如图 6所示。
在这个网络中, 每条边中{i, j=1, 2, 3, …, N}⊂E, 代表每条边中不同的节点进行双向通信。网络中的每个DESU仅将其状态传递给相邻的DESU, 并通过提供自身的线性方程来更新其状态。最后, 所有DESU的状态都能收敛至所需的平均值[14]。因此, Pref可由式(16)计算得到。
| $ \left\{\begin{array}{l} P_{\text {ref}i }[k+1]=P_{i}+\delta \sum\limits_{j \in N_{i}} \theta_{i j}[k+1] \\ \theta_{i j}[k+1]=\theta_{i j}[k]+P_{\text {ref}j }[k]-P_{\text {ref}i }[k] \end{array}\right. $ | (16) |
式中: Prefi——存储在DESUi中有功功率平均值;
δ——比例因子;
θij[k]——累积误差, 初值为0。
加入动态虚拟阻抗后的有功功率分配关系如图 7所示。由图 7可知, DESU1和DESU2的有功功率传输特性曲线斜率趋于一致, 从而消除了线路阻抗对有功功率分配精度的影响。
2.2 SOC平衡级控制
通过功率平衡级控制, 消除了不匹配线路阻抗对有功功率分配精度的影响。但是传统的下垂控制策略采用固定不变的下垂系数, 使得储能单元的SOC难以均衡。因此, 本文设计了基于e指数下垂的SOC平衡级控制, 即
| $ U_{i} =U^{*}-k_{p\_{i}} P_{i} $ | (17) |
| $ k_{p\_{i}} =\frac{k_{\mathrm{P}}}{\mathrm{e}^{N\left(E_{\mathrm{SOC}_{i}}-E_{\mathrm{SOC}_{\mathrm{ref}}}\right)}} $ | (18) |
式中: kp_i——DESUi实时P-V下垂系数;
N——加速因子;
ESOCref——荷电状态的平均值, 由动态一致性算法求得。
联立式(8)、式(17)和式(18)可得
| $ \Delta E_{\mathrm{SOC}_{i\_{j}}}=E_{\mathrm{SOC}_{i}}-E_{\mathrm{SOC}_{j}} $ | (19) |
式中, i, j∈[1, n], i≠j。
对式(19)进行求导
| $ \Delta \dot{E}_{\mathrm{SOC}_{i\_j}}=\dot{E}_{\mathrm{SOC}_{i}}-\dot{E}_{\mathrm{SOC}_{j}} $ | (20) |
| $ \begin{gathered} \Delta \dot{E}_{\mathrm{SOC}_{i\_j}}=\frac{1}{U_{\mathrm{DC}} C_{\mathrm{e}}}\left(P_{j}-P_{i}\right)=\frac{\left(U^{*}-U\right)}{U_{\mathrm{DC}} C_{\mathrm{e}} k_{\mathrm{P}}}\cdot \\ \left(\mathrm{e}^{N\left(E_{\mathrm{SOC}_{j}}-E_{\mathrm{SOC}_{\mathrm{ref}}}\right)}-\mathrm{e}^{N\left(E_{\mathrm{SOC}_{i}}-E_{\mathrm{SOC}_{\mathrm{ref}}}\right)}\right) \end{gathered} $ | (21) |
式中, U=Ui=Uj。
采用泰勒级数展开式, e指数函数的一阶展开式可近似表示为[15]
| $ \mathrm{e}^{x}=1+x $ | (22) |
将式(22)代入式(21), ΔESOCi_j的导数可近似表示为
| $ \Delta E_{\mathrm{SOC}_{i\_j}}=\frac{N\left(U^{*}-U\right)}{U_{\mathrm{DC}} C_{\mathrm{e}} k_{p}}\left(E_{\mathrm{SOC}_{j}}-E_{\mathrm{SOC}_{i}}\right) $ | (23) |
式(23)表明, ΔESOCi与ΔESOCj的误差和收敛速度正在逐渐变小, 最终实现SOC均衡, 避免DESU过放电。同时, ΔESOC的导数绝对值与N正相关, N越大, ΔESOC的导数的绝对值越大, 储能单元间SOC收敛速度越快。
根据上述分析, 利用SOC平衡级控制, 使得储能单元根据其SOC动态调节有功功率, 使得放电过程中SOC均衡。由于SOC的e指数下垂特性, 使得储能单元在SOC平衡级控制的初始阶段, 误差能够快速减小, 实现了SOC的快速收敛。同时, 在SOC平衡级控制的最后阶段, SOC的误差缓慢趋近于零, 可有效防止调节速度过快引起超调而生成新的误差。
2.3 小信号稳定性分析
为了便于分析, 仍以2台容量相等的并联DESU为例, 建立在平衡点附近的小信号模型并对其进行分析。以式(17)的有功功率-电压下垂特性曲线为例, 在系统稳定工作点附近给一个很小的扰动, 得到的工作点附近的线性化模型为
| $ \left\{\begin{array}{l} k_{p} \hat{P}_{1}=\mathrm{e}^{\frac{N}{2}\left(E_{\mathrm{SOC}_{1}}-E_{\mathrm{SOC}_{2}}\right)}\left[\frac{N}{2}\left(\tilde{U}^{*}-\tilde{U}_{1}\right) \hat{E}_{\mathrm{SOC}_{1}}-\hat{U}_{1}\right] \\ k_{p} \hat{P}_{2}=\mathrm{e}^{\frac{N}{2}\left(E_{\mathrm{SOC}_{2}}-E_{\mathrm{SOC}_{1}}\right)}\left[\frac{N}{2}\left(\tilde{U}^{*}-\tilde{U}_{2}\right) \hat{E}_{\mathrm{SOC}_{2}}-\hat{U_{2}}\right] \end{array}\right. $ | (24) |
式中, 上标“^”的变量表示对应量的小信号扰动分量, 上标“~”的变量表示对应量的稳态分量。
式(8)表示采用库伦计算法得到储能单元的SOC。对式(8)进行小信号扰动, 并将其结果变换到频域, 可得
| $ \left\{\begin{array}{l} s \hat{E}_{\mathrm{SOC}_{1}}=-\frac{\overset\frown{p}_{1}}{C_{\mathrm{e}} U_{\mathrm{DC}}} \\ s \hat{E}_{\mathrm{SOC}_{2}}=-\frac{\overset\frown{p}_{2}}{C_{\mathrm{e}} U_{\mathrm{DC}}} \end{array}\right. $ | (25) |
在使用下垂控制的过程中, 需要利用低通滤波器对输出瞬时功率进行滤波。滤波前后的功率关系为
| $ L\left(p_{i}\right)=G_{\mathrm{LPF}} L\left(P_{i}\right) $ | (26) |
| $ G_{\mathrm{LPF}}=\frac{\omega_{0}}{s^{2}+2 \xi \omega_{0} s+\omega_{0}^{2}} $ | (27) |
式中: L(.)——拉普拉斯变换;
GLPF——二阶低通滤波器;
ω0——滤波器截止频率;
ξ——衰减系数。
联立式(24)、式(25)和式(26), 可得
| $ \left\{\begin{array}{l} \hat{P}_{1}=-\frac{a_{1} G_{\mathrm{LPF}} s}{a_{1} b_{1}+k_{p} G_{\mathrm{LPF}} s} \hat{U_{1}} \\ \hat{P_{2}}=-\frac{a_{2} G_{\mathrm{LPF}} s}{a_{2} b_{2}+k_{p} G_{\mathrm{LPF}} s} \hat{U_{2}} \end{array}\right. $ | (28) |
其中
| $ \left\{\begin{array}{l} a_{1}=\mathrm{e}^{\frac{N}{2}\left(E_{\mathrm{SOC}_{1}}-E_{\mathrm{SOC}_{2}}\right)}, b_{1}=\frac{N\left(\tilde{U}^{*}-\tilde{U}_{1}\right)}{2 C_{\mathrm{e}} U_{\mathrm{DC}}} \\ a_{2}=\mathrm{e}^{\frac{N}{2}\left(E_{\mathrm{SOC}_{2}}-E_{\mathrm{SOC}_{1}}\right)}, b_{2}=\frac{N\left(\tilde{U}^{*}-\tilde{U}_{2}\right)}{2 C_{\mathrm{e}} U_{\mathrm{DC}}} \end{array}\right. $ |
负荷功率Pload由DESU1和DESU2共同承担, 且输出电压相等, 所以
| $ P_{1}+P_{2}=P_{\text {load }} $ | (29) |
| $ U_{1}=U_{2} $ | (30) |
对式(29)和式(30)进行小信号扰动, 并将结果变换到s域, 联立所得频域结果及式(26), 可得
| $ A s^{2}+B s+C=0 $ | (31) |
其中
| $ \left\{\begin{array}{l} A=a_{1} a_{2}\left(b_{1}+b_{2}\right) \\ B=2 a_{1} a_{2} \xi \omega_{0}\left(b_{1}+b_{2}\right)+k_{p} \omega_{0}^{2}\left(a_{1}+a_{2}\right) \\ C=a_{1} a_{2} \omega_{0}^{2}\left(b_{1}+b_{2}\right) \end{array}\right. $ |
根据式(31)所得特征方程对SOC平衡级控制的稳定性进行分析[16]。用于分析稳定性的系数参数如表 1所示。
表 1
控制参数及其取值
| 参数 | 取值 | 参数 | 取值 | |
| kp | 3.0×10-6 | U*/V | 311 | |
| U1, U2/V | 310 | ω0/(rad·s-1) | 126 | |
| ξ | 0.707 | Ce/Ah | 100 | |
| UDC/V | 600 |
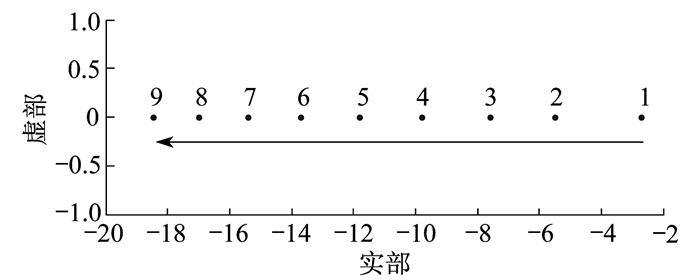
图 8为加速因子N在1~9的情况下系统主导极点的分布。各极点依次以序号1, 2, 3…, 9标明。
由图 8可知, 系统的主导极点均位于左半平面, 且随着N的增大, 主导极点远离虚轴, 系统越稳定, 保证了分级控制中SOC平衡级控制的稳定性。
3 仿真分析
3.1 传统下垂控制SOC不平衡验证
3.2 3台并联储能单元正常运行
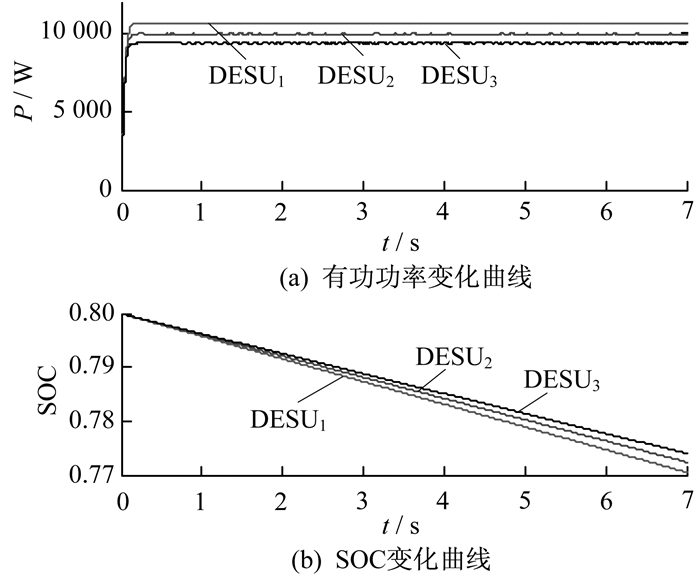
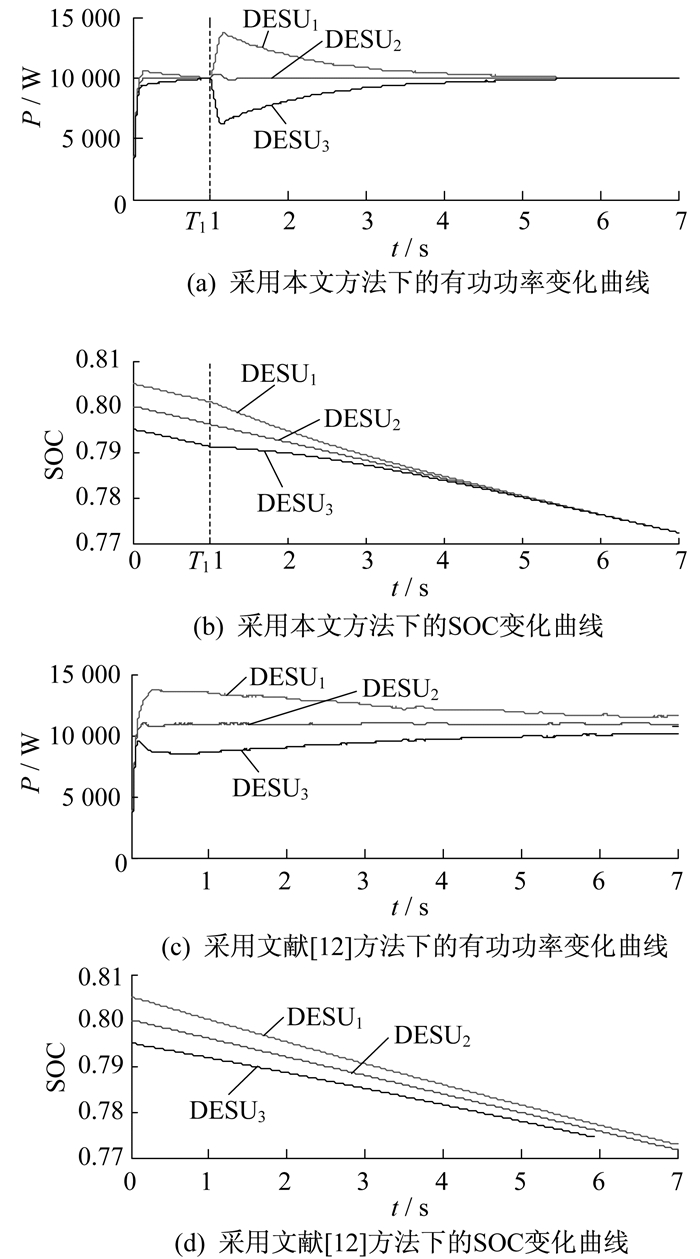
为了验证本文提出的控制策略, 设置各储能单元初始荷电状态ESOC1_0, ESOC2_0, ESOC2_0分别为80.5%, 80.0%, 79.5%。系统的仿真过程为: 0~T1, 各DESU工作在功率平衡级, 虚拟阻抗通过有功功率动态调整, 当系统稳定时, 各DESU的虚拟阻抗分别趋于稳定, 此时有功功率实现精确均分, 满足SOC均衡条件; T1时, 系统切换至SOC平衡级, 各个储能单元根据其荷电状态动态调节有功功率, 使得SOC误差以e指数曲线下降, 最终实现储能单元在充放电过程中SOC均衡。
3台储能单元正常运行的仿真图如图 10所示。
3.3 储能系统投切负荷
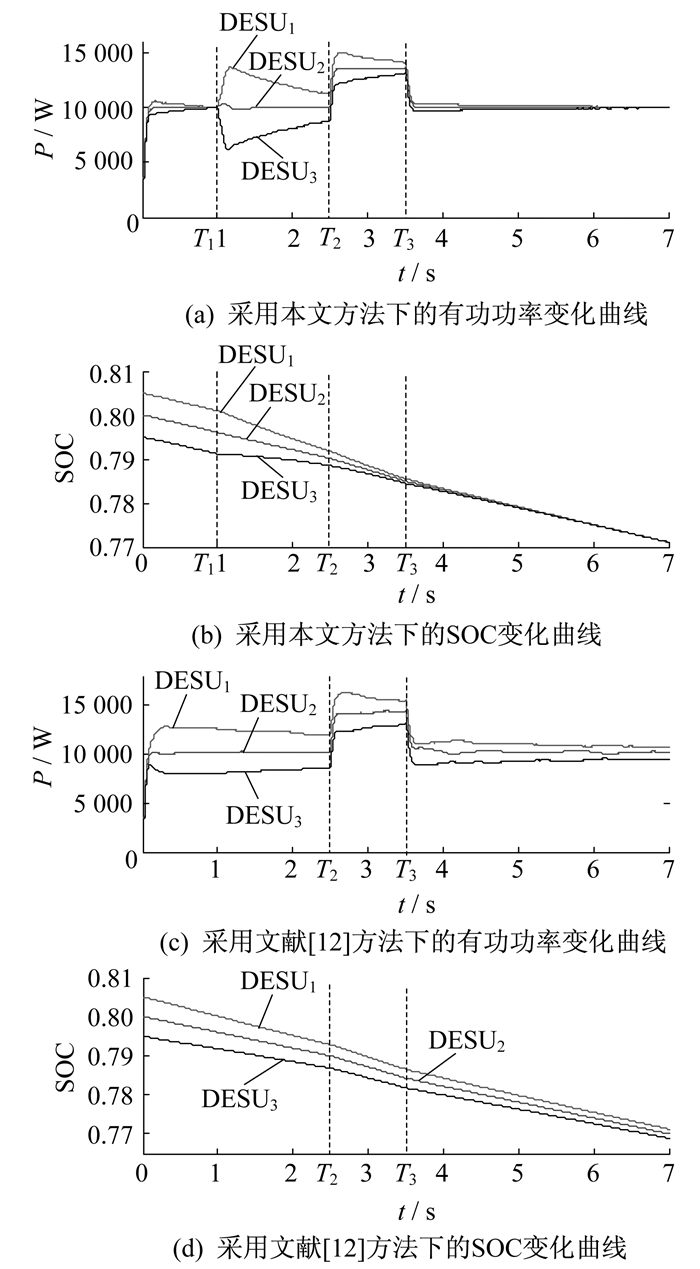
为了验证系统发生负荷波动对本文分级控制的影响, 设置各储能单元初始荷电状态ESOC1_0, ESOC2_0, ESOC2_0分别为80.5%, 80.0%, 79.5%。系统的仿真过程为: 0~T1, 各DESU工作在功率平衡级, 有功功率逐渐实现均分; T1时, 系统切换至SOC平衡级, DESU的SOC逐渐收敛; T2时切入10 kW负荷; T3时切除这个负荷。储能系统投切负荷仿真结果如图 11所示。
由图 11可知: 负荷大小并不影响SOC均衡的趋势, 只是改变了SOC均衡的速率; 相比于文献[12]中的方法, 分级控制能有效消除线路阻抗对有功功率均分的影响, 能使储能单元间的误差以e指数曲线下降, 波形平滑, 快速实现了SOC均衡, 避免了DESU的过放电, 提高了其安全性。
3.4 储能单元故障切除
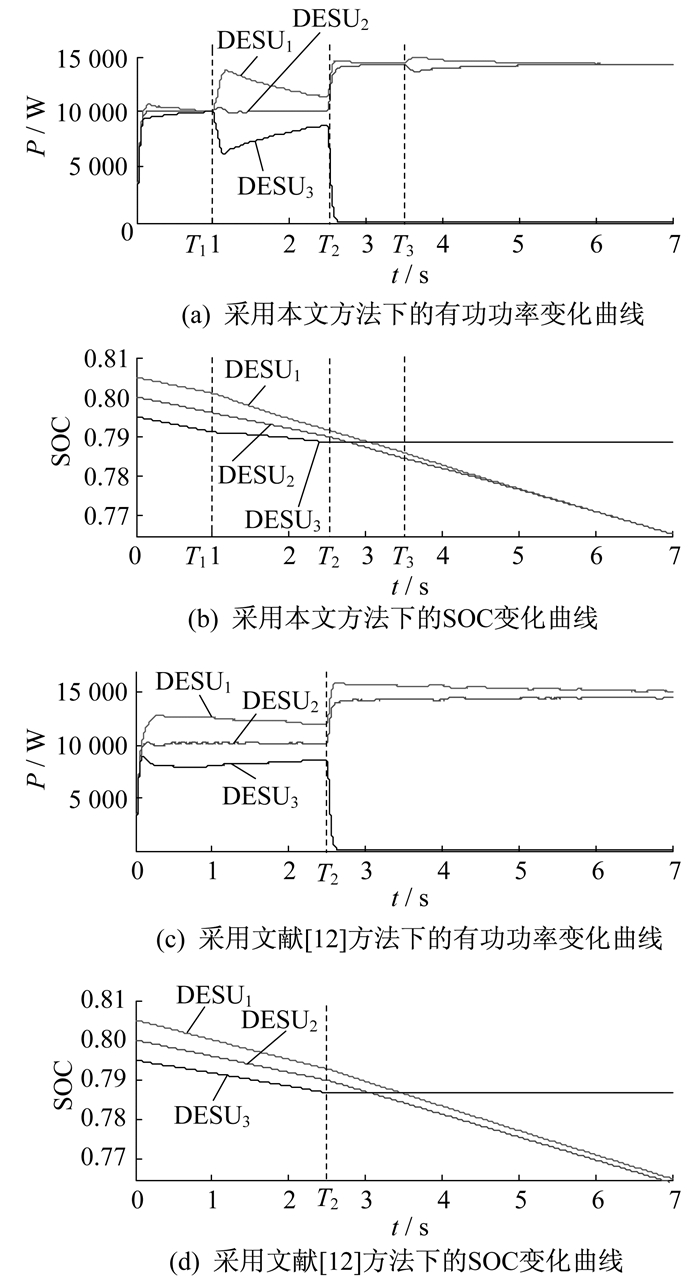
为了验证储能单元切除对分级控制策略的影响, 设置各储能单元初始荷电状态ESOC1_0, ESOC2_0, ESOC2_0分别为80.5%, 80.0%, 79.5%。各储能单元故障切除仿真结果如图 12所示。
由图 12可知, 0~T1, 各储能单元工作在功率平衡级, 系统消除了不匹配线路阻抗的影响, 有功功率能够分别精确均分, 满足SOC均衡条件; T1时, 各储能单元运行模式切换至SOC平衡级, 使得SOC误差以e指数曲线下降, 各DESU的SOC逐渐收敛; T2时, DESU3由于故障, 故对其进行切除, 只有DESU1和DESU2并联运行, 使得虚拟阻抗发生变化, 无法实现有功功率的精确均分, 需要重新进行功率平衡级控制; T3时, 再次切换至SOC平衡级, 系统误差缓慢趋于零, 最终实现SOC均衡, 避免了DESU的过放电, 提高了DESS的安全性。
4 结语
为了消除不匹配线路阻抗对有功功率分配精度的影响, 使得各储能单元SOC均衡, 本文提出了一种低压微电网分布式储能系统分级控制策略。通过功率平衡级和SOC平衡级控制, 使得储能单元在放电过程中SOC均衡。
本文提出的分级控制只需要每个DESU的本地和相邻信息, 因此只需要本地通信而不依赖于全局通信, 具有较高的可靠性和较强的鲁棒性, 并保持了每个DESU的“即插即用”特性。基于小信号理论对所提控制策略进行了稳定性分析, 并分析了加速因子N的作用, 通过调整N, 可快速实现多个储能单元SOC迅速均衡且不影响系统的稳定性。
参考文献
-
[1]张金星, 于艾清, 屠亚南, 等. 基于自适应虚拟阻抗的微电网分布式电源控制[J]. 上海电力学院学报, 2018, 34(6): 523-530. DOI:10.3969/j.issn.1006-4729.2018.06.003
-
[2]邓玮璍, 陈鹏飞. 基于ZigBee网络的低压微电网半实物仿真[J]. 上海电力学院学报, 2019, 35(4): 315-320.
-
[3]米阳, 蔡杭谊, 宋根新, 等. 考虑不匹配线阻的分布式储能单元荷电状态均衡研究[J]. 中国电机工程学报, 2019(15): 4441-4450.
-
[4]米阳, 蔡杭谊, 袁明瀚, 等. 直流微电网分布式储能系统电流负荷动态分配方法[J]. 电力自动化设备, 2019, 39(10): 17-23.
-
[5]NGUYEN N, ORUGANGMIN S K, NA K, et al. An adaptive backward control battery lithium-ion battery[J]. IEEE Transactions on Vehicular Technology, 2014, 63(8): 3651-3660. DOI:10.1109/TVT.2014.2304453
-
[6]陆晓楠, 孙凯, 黄立培, 等. 直流微电网储能系统中带有母线电压跌落补偿功能的负荷功率动态分配方法[J]. 中国电机工程学报, 2013, 33(16): 37-46.
-
[7]LU X, SUN K, GUERRERO J M, et al. State-of-charge balance using adaptive droop control for distributed energy storage systems in DC microgrid applications[J]. IEEE Transactions on Industrial Electronics, 2013, 61(6): 2804-2815.
-
[8]米阳, 吴彦伟, 纪宏澎, 等. 基于多组储能动态调节的独立直流微电网协调控制[J]. 电力自动化设备, 2017(5): 170-176.
-
[9]DIAZ N L, DRAGIČEVIĆ T, VASQUEZ J C, et al. Intelligent distributed generation and storage units for DC microgrids-a new concept on cooperative control without communications beyond droop control[J]. IEEE Transactions on Smart Grid, 2014, 5(5): 2476-2485. DOI:10.1109/TSG.2014.2341740
-
[10]王炜信, 段建东, 张润松, 等. 孤岛电网中多储能设备SOC一致性优化策略[J]. 电工技术学报, 2015, 30(23): 126-135. DOI:10.3969/j.issn.1000-6753.2015.23.016
-
[11]陆晓楠, 孙凯, 黄立培, 等. 孤岛运行交流微电网中分布式储能系统改进下垂控制方法[J]. 电力系统自动化, 2013, 37(1): 180-185.
-
[12]孙孝峰, 郝彦丛, 王宝诚, 等. 微电网分布式储能单元荷电状态平衡和电压恢复[J]. 中国电机工程学报, 2016, 36(15): 4047-4054.
-
[13]孙孝峰, 陈敬娴, 田艳军, 等. 基于虚拟微调阻抗微网多DG功率均分控制策略[J]. 太阳能学报, 2015, 36(5): 1162-1170. DOI:10.3969/j.issn.0254-0096.2015.05.022
-
[14]MENG L, ZHAO X, TANG F, et al. Distributed voltage unbalance compensation in islanded microgrids by using a dynamic consensus algorithm[J]. IEEE Transactions on Power Electronics, 2015, 31(1): 827-838.
-
[15]王杰. 高等数学[M]. 重庆: 重庆大学出版社, 1990: 261-280.
-
[16]胡寿松. 自动控制原理[M]. 北京: 科学出版社, 2013: 93-101.