|
|
|
发布时间: 2021-12-28 |
智能电网技术 |
|
|
|
收稿日期: 2020-03-18
基金项目: 国家自然科学基金面上项目(61772327);国家自然科学基金重点项目(61532021)
中图法分类号: TP399;TM712
文献标识码: A
文章编号: 2096-8299(2021)06-0539-07
|
摘要
随着能源互联网中大量电力智能终端的部署,有效评估电力终端的安全性显得尤为重要。针对现有方案存在选取指标因素不全面、未对权重结果进行验证和评价结果主观性太强等问题,根据电力终端风险评估需求,提出了基于层次分析法的电力终端安全评估方案,模拟实验数据获取指标权重,引入模糊综合评价法来降低评估结果的片面性。实验结果表明,和已有方案相比,该方案更适用于电力终端安全评估,能有效发现存在的安全风险,且评估结果更接近实际情况。
关键词
电力终端; 安全评估; 层次分析法; 模糊综合评价法
Abstract
With the deployment of a large number of power smart terminals in the Energy Internet, it is particularly important to effectively evaluate the security of power terminals.Existing schemes have the problems of incomplete selection of index factors, failure to verify the weighting results and too subjective evaluation results.According to the needs of power terminal risk assessment, a power terminal safety evaluation scheme based on Analytic Hierarchy Process is proposed.Simulation experiment data is used to obtain index weights, and fuzzy comprehensive evaluation method is introduced to reduce the one-sidedness of evaluation results.Results show, compared with existing schemes, this scheme is more suitable for power terminal safety assessment.It can effectively find the existing safety risks, and the assessment result is closer to the actual situation.
Key words
power terminal; security assessment; analytic hierarchy process; fuzzy comprehensive evaluation method
随着能源互联网的发展, 大量的电力终端被投入使用。电力终端是位于用户侧的电子设备, 例如智能电表、电力传感器、DTU数据采集与监控终端单元、RTU远程终端单元和FTU馈线开关监控终端单元等。电力终端的功能包含采集电力数据、调控电力生产、传输通信数据以及电网状态监测等。
电力终端的安全可靠是电力系统稳定运行的根本[1]。各类用电采集终端在智能电网建设中得到了广泛应用, 但是由于采集终端本身结构简单、用户行为无安全管控行为、采集终端部署环境较为恶劣等问题, 所以造成终端存在着大量的安全隐患[2]。在用户用电过程中, 恶意攻击者可以通过攻击电力终端来盗取电力隐私数据。这些隐私数据中包含了大量的用户及电力系统的敏感信息。在电力终端紧密连接馈电线路情况下, 攻击者还可以干扰电力正常生产调度流程。电力系统智能终端计算环境安全保证不足, 存在终端被恶意控制破坏的风险[3]。因此, 建立电力终端安全评估体系和对电力终端系统信息安全风险评估是非常重要迫切的工作。
现有的电力系统风险评估方案仅考虑了一部分终端安全因素, 并不完全适用于电力终端的安全评测, 同时存在考虑指标因素不全面、未对指标权值进行验证以及评价结果主观性太强等问题。
LIAO H等人[4]建立了一个网络终端安全状况评估的4级指标体系, 将网络终端安全状况划分为5级, 等级越高风险越大, 其建立的评估指标体系主要工作对象为主机和工作站, 即互联网应用终端, 并不适用于电网中的终端设备。傅宏等人[5]也建立了网络终端安全状况的评估指标体系, 对该指标体系进行定量、定性及综合风险评估, 建立了网络终端安全评估系统, 并提出了终端安全评估的系统流程模块, 但是同样不适用于电力系统的终端设备。LIU M等人[6]基于层次分析法和模糊仿真完成了电网灾难性事故风险评估, 最终得到的结果有助于维修人员的决策, 但该方案利用层次分析法对整个电网进行的风险评估没有具体到电力终端的安全评价。宗祥瑞等人[7]利用熵权法对电网运行状态特征进行分析评价, 通过熵的概念来描述电网负载水平, 但客观赋权需要大量数据支撑, 许多属性难以获取准确数据。杨杉等人[8]认为电网信息系统中的信息安全风险主要来自于系统本身以及配置错误而引发的问题, 基于这两类风险确定了3层指标体系, 计算各模块相对总评估目标的组合权重, 但该方案对电网信息系统进行安全评估, 并不完全适用于电力终端。罗艳等人[9]通过随机森林的方法对电网实时运行风险进行评估, 需要利用历史数据对随机森林智能体训练, 模型较为复杂, 不适用于对电力终端整体情况的评估。LIU R等人[10]利用堆叠降噪自编码器(Stacked Denoising Auto Encoder, SDAE)提取故障数据的特征, 利用层次贝叶斯模型对配电终端的故障率数据进行评估, 但模型对整体评估性能较弱。XIE G等人[11]通过模糊层次分析法对采集终端的运行状态进行了评估, 但未涉及其他类型的电力终端。CHEN L[12]建立电力移动终端的层次分析模型, 但是在求解指标体系各因素权重时, 未对指标进行量化分析。孙歆等人[13]提出基于层次指标体系的电力移动终端安全评估方法, 通过编写Agent去调用API(Application Programming Interface)来获取指标数据信息。但是该方案未考虑电力固件安全, 在用层次分析法获取指标权重时没有考虑不同计算方法的验证。
电力系统中终端的可管、可信、可用, 是终端安全的基础[14], 在选取指标因素构建层次结构的时候, 需要将《电力行业信息系统安全等级保护基本要求》和实际电力系统需求相结合。针对目前电力终端安全评估存在的问题, 本文提出了基于层次分析法的电力终端安全评估方案, 综合考虑电力行业标准和电力系统实际需求构建合理的电力终端安全指标体系, 结合模糊综合评价法(Fuzzy Comprehensive Evaluation Method,FCEM)计算得到电力系统中终端安全的最终评估值。
1 电力终端安全评估指标体系
1.1 建立指标体系的流程
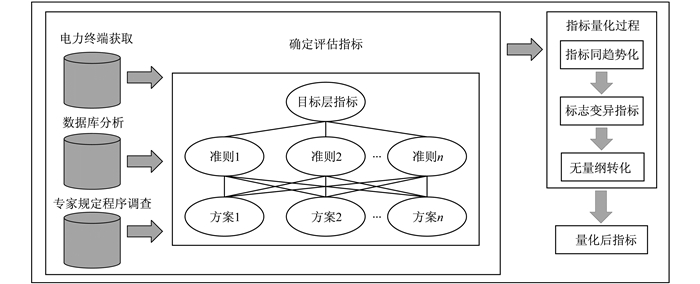
综合考虑评估电力终端安全涉及到的指标因素, 采用德尔菲法确定评估指标, 通过指标同趋势化、标志变异指标和无量纲转化对所选取的评估指标进行量化。建立电力终端安全评估指标体系的流程如图 1所示。
1.2 确定评估指标
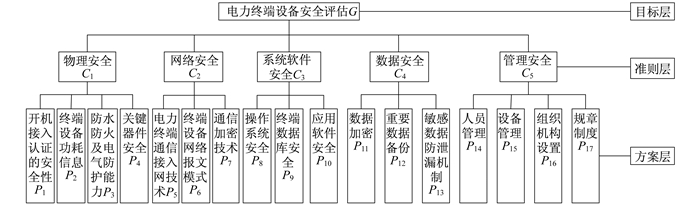
由于电力终端设备种类繁多, 且电力终端的安全涉及内容广泛且复杂, 所以在设计构建电力终端安全评估指标体系时, 参考电力行业标准涉及内容, 并利用专家规定程序调查法[15], 综合考虑指标因素的合理性。在电力信息系统终端设备的应用过程中, 其信息安全风险主要来源于两个方面: 一方面是物理硬件设置、网络配置规划、系统应用软件中的漏洞; 另一方面是在终端设备的安全管理方面存在的风险隐患。最终形成指标体系3层结构如图 2所示。
建立的指标体系可以满足实际场景中电力终端安全评估的需要。该指标体系共有3层: 目标层、准则层和方案层。目标层指标分为物理安全、网络安全、系统软件安全、数据安全和管理安全5大准则。这5个准则层指标又细化分为17个方案层指标, 涵盖了电力终端设备安全评估的各个方面因素。
1.3 量化评估指标
为了保证整个评估方案的科学性、准确性, 需要对所有的指标因素进行量化处理。利用数学变换来统一评估值的趋势, 完成评估指标的量化。
量化过程包括3个步骤: 主成分分析中指标同趋势化、标志变异指标的标识和无量纲转化。若评估指标体系中使用了多项指标, 需要先将指标同趋势化, 把所有的指标方向一致化[16]。其方法可分为逆向指标正向化和适度指标正向化。指标同趋势化方法及含义解释如表 1所示。
表 1
指标同趋势化方法及含义解释
| 方法 | 含义解释 |
| Xi*=-Xi | 逆向指标取负值为其替代指标 |
| 逆向指标取倒数为其替代指标 | |
| 逆向指标取指标最大的绝对值加上原始值再取倒数为其替代指标 | |
| 适度指标取原始值Xi与其适度值Sui之差的绝对值的倒数为其替代指标 |
标志变异指标可以用于反映总体各单位标志值之间的差异程度或离散程度。测量标志变异指标来标识出该指标是否需要消除指标变异程度上的差异, 如果需要消除, 就采取指标数据标准化的办法, 当不能消除变异程度大的指标数据时, 采用均值法。
在构建评估指标体系时, 各个评价指标的量纲和表现形式对总目标的作用趋向各不相同, 需要进行指标的无量纲转化来消除量纲与量纲单位的影响。具体的指标无量纲转化方法可以分为直线型、折线型和曲线型3种, 根据指标数据的变异程度来选择相应的量纲转化方法。
2 基于层次分析法的电力终端安全评估方案
2.1 构造判断矩阵
为了对各个指标因素进行准确量化, 可以用尺度1~9度量将模糊问题定量化, 假设给定2个指标因素Ind1和Ind2, 其定性结果和对应的定量结果如表 2所示。
表 2
指标定性结果和对应的定量结果
| 定性结果 | 定量结果 |
| Ind1和Ind2具有相同重要性 | Ind1∶Ind2=1∶1 |
| Ind1比Ind2重要 | Ind1∶Ind2=3∶1 |
| Ind1比Ind2明显重要 | Ind1∶Ind2=5∶1 |
| Ind1比Ind2强烈重要 | Ind1∶Ind2=7∶1 |
| Ind1比Ind2极端重要 | Ind1∶Ind2=9∶1 |
| Ind1和Ind2的重要程度在上述4个等级之间 | Ind1∶Ind2={2, 4, 6, 8}∶1 |
| Ind1和Ind2的重要程度和上述情况相反 | Ind1∶Ind2=1∶{1, 2, …, 9} |
根据表 2构造判断矩阵为
| $ \mathit{\boldsymbol{A}} = {\left( {{a_{ij}}} \right)_{n \times n}} = \left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}& \cdots &{{a_{1n}}}\\ {{a_{21}}}&{{a_{22}}}& \cdots &{{a_{2n}}}\\ \vdots & \vdots & \vdots & \vdots \\ {{a_{n1}}}&{{a_{n2}}}& \cdots &{{a_{nn}}} \end{array}} \right] $ | (1) |
式中: aij——指标i和指标j相比的重要程度, aij>0, aij×aji=1。
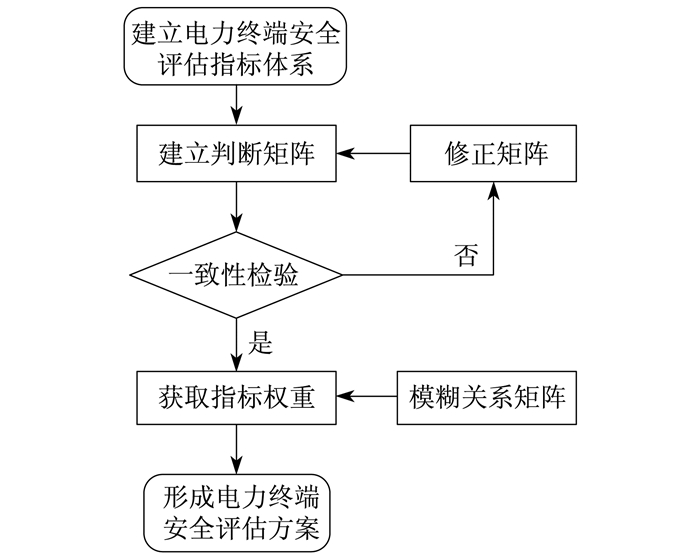
2.2 检验层次一致性
构造完判断矩阵后, 需要对指标因素进行层次一致性检验。如果通过, 判断矩阵就可以用来计算各指标因素的权重, 否则进行矩阵的修正。
首先, 计算判断矩阵A的最大特征值λmax和其对应的特征向量ai; 对判断矩阵A进行行列规范化, 得到表达式
表 3
n阶判断矩阵对应RI值
| n | RI | n | RI | n | RI | n | RI | |||
| 1 | 0 | 4 | 0.89 | 7 | 1.36 | 10 | 1.49 | |||
| 2 | 0 | 5 | 1.12 | 8 | 1.41 | 11 | 1.52 | |||
| 3 | 0.52 | 6 | 1.26 | 9 | 1.46 | 12 | 1.54 |
通过查找表 3找到相应的RI, 计算一致性比例为CR=CI/RI。当CR < 0.10时, 认为判断矩阵的一致性是可以接受的, 否则应对判断矩阵作适当修正。
2.3 获取指标因素权重
判断矩阵通过层次一致性检验后, 计算各个指标因素的权重配比, 算数平均法获取指标因素权重的公式为
| $ {W_i} = \frac{1}{n}\sum\limits_{j = 1}^n {\frac{{{a_{ij}}}}{{\sum\limits_{k = 1}^n {{a_{kj}}} }}, i = 1, 2, 3, \cdots , n} $ | (2) |
几何平均法获取指标因素权重的公式为
| $ {W_i} = \frac{{{{\left( {\prod\limits_{j = 1}^n {{a_{ij}}} } \right)}^{\frac{1}{n}}}}}{{\sum\limits_{k = 1}^n {{{\left( {\prod\limits_{j = 1}^n {{a_{kj}}} } \right)}^{\frac{1}{n}}}} }}, i = 1, 2, 3, \cdots , n $ | (3) |
特征值获取指标因素权重的过程如下: 根据最大特征值λmax求得对应的特征向量; 对求得的特征向量进行归一化处理, 最终得到权重向量。
2.4 模糊综合评价值
根据得到的上层指标对下层指标的权重向量, 采取模糊综合评价的方法构建评价矩阵, 建立适合的隶属函数从而构建好评价矩阵, 完成评价矩阵和权重的合成。
定义电力终端安全模糊综合评价的评价集为D={很好, 好, 一般, 差, 很差}和评价指标集合U。构建的电力终端安全评估指标体系为目标层—准则层—方案层的3层结构。在考虑目标层对于准则层的评价指标集合时, UG={物理安全, 网络安全, 系统软件安全, 数据安全, 管理安全}; 在考虑准则层对方案层的评价指标集合时, UCi集合中包含的是每个准则层指标对应的方案层指标。
定义Nijk为专家对第i个准则层指标中第j个准则层指标的第k个评价的频数, 计算评判权重系数
| $ \begin{array}{l} \mathit{\boldsymbol{S}} = \mathit{\boldsymbol{W}}*\mathit{\boldsymbol{R}} = \left[ {{W_1}\;\;\;{W_2}\;\;\; \cdots \;\;\;{W_m}} \right]*\\ \left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}& \cdots &{{r_{1n}}}\\ {{r_{21}}}&{{r_{22}}}& \cdots &{{r_{2n}}}\\ \vdots & \vdots & \vdots & \vdots \\ {{r_{m1}}}&{{r_{m2}}}& \cdots &{{r_{mn}}} \end{array}} \right] \end{array} $ | (4) |
其中, *为算子符号, 称之为模糊变换。
对综合评价矩阵S进行矩阵的归一化得到综合评价值。
3 实验过程及结果
3.1 实验环境设计
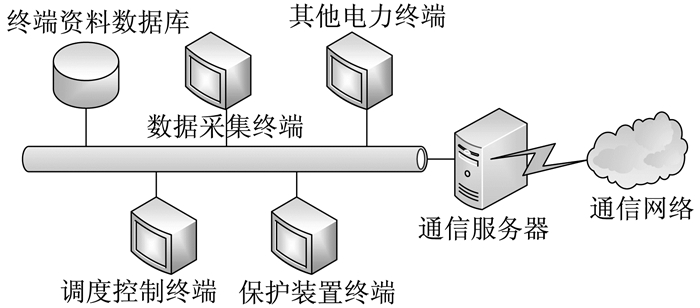
结合本文提出的电力终端安全评估方案, 设计了该方案的实验应用环境, 如图 4所示。各终端设备连接在数据总线上, 通过调用API来获取数据, 或直接通过相应的APP工具进行采集。终端资料数据库负责存放各终端的详细状态信息, 同时保留安全情况下各属性的状态备份, 通过对比可以发现各因素的异常变化, 进而在模糊层次分析中为专家程序调查提供评价依据。该仿真系统通过通信网络和其他电力系统相连接, 实现数据交互功能。
3.2 模拟实验过程
为了验证本文提出方案的有效性, 综合考虑电力系统中终端安全等级保护行业规范, 调用应用程序接口获取信息, 形成一组模拟数据作为构造判断矩阵的指标定量结果。目标层指标G和准则层指标{C1, C2, C3, C4, C5}对应的判断矩阵GC为
| $ {\mathit{\boldsymbol{G}}_{\rm{C}}} = \left[ {\begin{array}{*{20}{c}} 1&1&1&{1/4}&1\\ 1&1&{1/2}&{1/4}&1\\ 1&2&1&{1/5}&{1/3}\\ 4&4&5&1&3\\ 1&1&3&{1/3}&1 \end{array}} \right] $ | (5) |
各准则层指标和方案层指标之间形成相应的判断矩阵CiP。
构造判断矩阵后, 利用MATLAB编程得到矩阵最大特征值并进行层次一致性检验。经过计算得到的具体各层权重归类如表 4所示。在层次分析中对不同获取权重值的方法进行比较, 3种方法下判断矩阵GC得到的权重值结果差异不大, 权重配比合理。
表 4
各层指标权重归类结果
| 目标层 | 准则层 | 方案层 | |||||
| 指标 | 权重 | 指标 | 权重 | 指标 | 权重 | ||
| G | 1 | C1 | 0.122 5 | P1 | 0.081 3 | ||
| P2 | 0.475 8 | ||||||
| P3 | 0.154 5 | ||||||
| P4 | 0.2884 | ||||||
| C2 | 0.112 9 | P5 | 0.137 3 | ||||
| P6 | 0.623 2 | ||||||
| P7 | 0.239 5 | ||||||
| C3 | 0.118 7 | P8 | 0.163 8 | ||||
| P9 | 0.539 0 | ||||||
| P10 | 0.297 3 | ||||||
| C4 | 0.477 2 | P11 | 0.745 6 | ||||
| P12 | 0.134 3 | ||||||
| P13 | 0.120 1 | ||||||
| C5 | 0.168 7 | P14 | 0.136 1 | ||||
| P15 | 0.280 0 | ||||||
| P16 | 0.115 2 | ||||||
| P17 | 0.468 7 | ||||||
得到指标因素的权重矩阵后, 根据电力终端安全模糊综合评价集模拟专家经验数据, 评价电力系统中终端的安全风险状况, 得到各准则评价等级频数分布如表 5所示。最终归一化后得到的模糊评价向量为[0.415 9 0.712 4 1 0 0.091 2], 不同时空分布下该向量的变化可以反映电力系统中终端安全的风险评估状况。
表 5
准则指标评价等级频数
| 准则层 | 很好 | 好 | 一般 | 差 | 很差 |
| C1 | 2 | 5 | 10 | 1 | 2 |
| C2 | 3 | 4 | 8 | 4 | 1 |
| C3 | 6 | 3 | 7 | 2 | 2 |
| C4 | 5 | 7 | 7 | 1 | 0 |
| C5 | 1 | 4 | 4 | 2 | 9 |
3.3 方案效果评估
4 结语
针对能源互联网中电力终端安全风险评估问题, 综合考虑行业规范以及实际需求, 建立了更适用于电力终端的安全评估指标体系。通过终端应用程序接口、现有工具获取以及数据库资料分析, 结合专家规定程序调查, 保证指标选取的全面性。在利用层次分析法计算指标因素权重的过程中, 对比基于算数、几何和特征值3种不同的权值获取办法, 验证了结果合理性。通过模糊综合评价方法, 最终得到一组可以综合反映电力系统中终端安全状态的归一化向量。通过设计实验环境和模拟实验数据, 与以往的方案进行了效果对比, 结果说明了本文提出方案的有效性。下一步将针对增强层次分析法评估电力终端安全结果的客观性展开研究。
参考文献
-
[1]KHURANA H, HADLEY M, LU N, et al. Smart-grid security issues[J]. IEEE Security & Privacy, 2010, 8(1): 81-85.
-
[2]李红娇, 王晓飞. 面向用电采集系统终端的可信度量方案[J]. 上海电力学院学报, 2019, 35(3): 236-241. DOI:10.3969/j.issn.1006-4729.2019.03.008
-
[3]张涛, 赵东艳, 薛峰, 等. 电力系统智能终端信息安全防护技术研究框架[J]. 电力系统自动化, 2019, 43(19): 59-67.
-
[4]LIAO H, LING J. Research on network terminal security assessment index system[J]. Computer Engineering and Design, 2010(5): 47-50.
-
[5]傅宏, 蒲箭, 邱林, 等. 试析网络终端安全状况的评估指标体系[J]. 电子技术与软件工程, 2015(19): 209-211.
-
[6]LIU M, YAO G, TIAN J, et al. Risk assessment of power grid catastrophic accident based on AHP and fuzzy simulation[C]//IEEE International Conference on Applied Superconductivity & Electromagnetic Devices. Beijing, China: IEEE, 2013: 18-21.
-
[7]宗祥瑞, 昌冲. 基于熵权法的电网运行状态特征分析与评价[J]. 电力系统及其自动化学报, 2016(增刊1): 1-5.
-
[8]杨杉, 曹波. 层次分析法在电网信息系统安全评估分析中的应用[J]. 计算机与数字工程, 2011(10): 157-160. DOI:10.3969/j.issn.1672-9722.2011.10.041
-
[9]罗艳, 肖辅盛, 王庭刚, 等. 基于随机森林的电网实时运行风险评估方法[J]. 信息技术, 2020, 44(4): 23-26.
-
[10]LIU R, FENG S, CAI Y, et al. State assessment and fault prediction method of distribution terminal based on SDAE and hierarchical bayesian[C]//2019 IEEE Sustainable Power and Energy Conference(iSPEC). Beijing, China: IEEE, 2019: 2783-2787.
-
[11]XIE G C, LUO K B, ZENG Y, et al. Acquisition terminal status evaluation based on fuzzy analytic hierarchy[C]//2019 International Conference on Computer Network, Electronic and Automation(ICCNEA). Xi'an, China: IEEE, 2019: 19193193.
-
[12]CHEN L, LI N, CHEN M, et al. Power mobile terminal security risk assessment based on AHP[C]//International Conference on Smart Grid & Electrical Automation. Changsha, China: IEEE, 2018: 126-130.
-
[13]孙歆, 戴桦, 李沁园, 等. 基于层次分析法的电力移动终端安全评估方法[J]. 沈阳工业大学学报, 2018, 40(6): 9-15.
-
[14]刘成龙, 申培培, 辛晓鹏. 基于电力行业的终端信息安全防护[J]. 网络安全技术与应用, 2017(8): 143-144. DOI:10.3969/j.issn.1009-6833.2017.08.083
-
[15]HSU Y L, LEE C H, KRENG V B. The application of fuzzy delphi method and fuzzy AHP in iubricant regenerative technology selection[J]. Expert Systems with Applications, 2010, 37(1): 419-425. DOI:10.1016/j.eswa.2009.05.068
-
[16]陈军才. 主成分与因子分析中指标同趋势化方法探讨[J]. 统计与信息论坛, 2005(2): 20-24.
-
[17]杨博, 赵娟, 唐玮, 等. 基于层次分析法的电网科技项目综合评价方法研究[J]. 电气技术, 2017(4): 90-94. DOI:10.3969/j.issn.1673-3800.2017.04.017
-
[18]温杰, 楚瀛, 彭富强, 等. 层次分析法在继电保护系统可靠性研究中的应用[J]. 上海电力学院学报, 2016, 32(1): 35-40.