|
|
|
发布时间: 2022-02-28 |
清洁安全发电 |
|
|
|
收稿日期: 2020-03-18
中图法分类号: TM734
文献标识码: A
文章编号: 2096-8299(2022)01-0009-08
|
摘要
基于改进的粒子群算法(PSO)和遗传算法(GA)的动态经济调度模型, 充分考虑风电、火力发电的成本及碳排放交易的利润, 并通过PSO结合GA模型, 计算出了风力发电和火电在一定时间内的实际发电量, 能够满足负荷需求; 并且根据碳交易的制度, 在保证低碳发展的同时, 获取了最低的经济成本。改进算法的运用, 提高了算法的效率, 保证了结果的稳定, 并且避免了陷入局部最优解的问题。实验结果证明了模型的可行性。
关键词
经济调度; 碳排放交易; 风电并网; 粒子群算法; 遗传算法
Abstract
As the carbon trading market has been initially established and the low-carbon economy has gradually entered the era.How to achieve wind power access and carbon trading, and to achieve flexible scheduling is very important.The model has considered the costs of wind and thermal power generation, as well as the profits of carbon trading, and established a low-carbon economic scheduling model function with multiple uncertainties.The actual power generation of wind power and thermal power in a certain period is calculated by PSO combined with GA model, which can meet the load demand.By the carbon trading system, low-carbon development is guaranteed while achieving the lowest economic costs.Improvised algorithm applications improve the efficiency of the algorithm, make the results stable, and avoid the problem of getting into the local optimal solution.The experimental results prove the feasibility of the model.
Key words
economic dispatch; carbon emission; wind power prediction; particle swarm optimization; genetic algorithm
随着风电并网容量持续增多, 风电出力的不确定性给系统的优化调度带来了一系列的问题。风电并网对系统的影响和冲击与其他火力发电机组一样, 但由于风速的随机性导致风电场的出力也是随机的, 风电本身的这些特点使得其容量可信度低, 影响电能质量, 因此在提高风电的利用率、减少弃风现象的同时, 系统要预留一定的备用容量。在火电预留充分容量的同时, 需要针对风力发电情况制定相对应的火力机组发电计划。对于未来一天的发电计划的制定, 若能够获得精细的风力发电预测, 进而制定对应的火力发电厂发电计划及风电备用容量, 能在一定程度上缓解风电随机性对系统造成的冲击。
含风电场的电力系统调度主要是针对风电并入火电的联合调度, 近年来逐渐开始关注环境问题。文献[1]根据火力发电机组的排污特性引入环境污染惩罚函数及风电环境价值, 提出了火电机组环境补偿成本, 并且考虑系统功率平衡、机组爬坡率等约束条件。文献[2]将风电场电力系统调度的影响因素作为研究对象, 在调度模型中针对风力发电量的出力偏差, 考虑了正、负旋转备用容量约束。文献[3]建立了风电的运行成本模型, 并网预测误差成本, 提出了广义的风力发电成本, 并将风电场备用容量的补偿成本引入到风电的广义运行成本中。文献[4]考虑了风电接入电网带来的停电损失及弃风损失, 并将其纳入风险成本中, 建立了电力系统调度及备用决策模型。
针对含风电电力系统中不确定变量, 研究者尝试利用多场景技术[5-6]来处理变量的不确定性。文献[7]根据买入客服链原理进行了建模。文献[8]利用多场景技术处理了在碳交易下含风电调度系统中, 因风电具有的随时间变化特性而增加多场景技术处理不确定变量的问题。
为了建立一种更好的模型减少风电随机性对系统的冲击, 大量文献提出了对应的解决办法。文献[9]提出了通过改进的粒子群优化(Particle Swarm Optimization, PSO)算法建立的新的随机约束模型来解决风电的不确定性成本。文献[10]将风力发电和抽水蓄能电站相结合, 提高电力系统可再生能源的高渗透水平。文献[11]明确了风电功率随风速等气象原因变化的数学表达式, 建立了风力发电和储能系统控制调度优化模型。
作为主要的二氧化碳排放源, 电力行业碳化是应对全球气候变暖这一挑战的关键和基础。传统燃煤式发电机是导致碳排放的关键。因此, 将当前的电力结构转换为低碳结构至关重要。
碳排放交易的启动可以影响火电机组的发电成本, 使清洁能源发电更具优势。在现有文献中, 许多学者结合CO2排放, 提出了多种智能算法和数学方法来解决火-风发电机组的最优经济性问题。文献[12]提出CO2的排放量不仅直接受CO2排放价格的影响, 还可能影响能源市场(如化石燃料价格)的其他因素, 这些因素可能直接影响到CO2排放政策。除了CO2的价格和政策外, 由于风电并网规模的增大, 所以预测误差对经济的影响也越来越明显。为此, 文献[13]引入可信性理论和模糊机会约束调度方法, 解决了风电系统调度的模糊机会决策问题。WANG C X等人[14]将碳排放作为一个虚拟网络流, 在分析碳排放和电力行业发展趋势的基础上, 构建了电力系统碳排放的理论框架。文献[15]站在消费者的角度, 分析了制定CO2减排政策的必要性, 结合电力系统特点, 提出了碳排放流测概念, 并将其应用于电力负荷的碳排放计算。文献[16]研究了跨区域电力交易中碳排放权界定问题, 构建了基于碳流量追踪的数学模型。
本文提出的基于改进PSO和遗传算法(Genetic Algorithm, GA)的动态低碳调度模型包括3个调度目标: 低碳经济低碳调度目标、最小火电经济成本和风力发电。在模型的构建中, 提出的低碳经济调度目标兼顾了能源生产的经济性和系统的低碳排放, 可以实现多目标问题的最优化求解。
1 模型框架
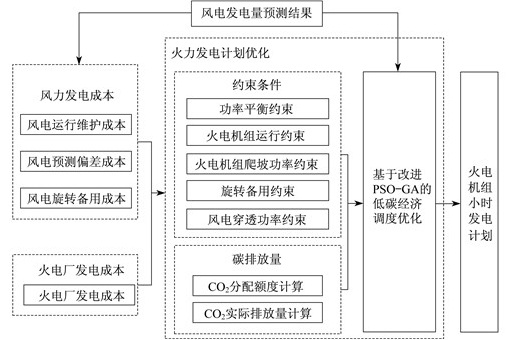
基于改进PSO和GA的动态低碳调度模型框架如图 1所示。
模型包括4个部分: 风电和火电的发电成本、保证电源区安全稳定供电的约束条件、碳交易机制、基于改进的PSO和GA进行火力发电机组的发电量计算。
对风力发电成本、火电厂发电成本和保证电源区安全稳定供电的约束条件, 建立了相关的数学模型, 进行含风电调度的动态经济分析。结合碳交易机制, 并使用改进的PSO和GA进行火力发电机组的发电量计算, 进行低经济调度分析。
2 风电和火电的发电成本
风电并网的成本, 主要包括风力发电成本和火电厂发电成本。
2.1 风力发电成本
文献[17-18]指出风电成本主要来自于4个方面: 风力并网成本、风力发电成本、辅助服务成本和环境效益。此外, 由于风电的随机性和波动性, 风电接纳也会带来额外的成本[19-20]。在常规的风电并网成本基础上, 本文介绍了通过风力发电的备用容量应对因风电功率预测偏差引起的系统波动。
在考虑风电运行和维护费用的基础上, 本文将风电全寿命周期内的平均发电成本Fm近似地表示为与发电量的线性关系。
| $ F_{\mathrm{m}}=\sum\limits_{t=1}^{T} C_{\mathrm{m}} P_{\mathrm{W}, j t} $ | (1) |
式中: Cm——风机在时间段t内的发电成本, 元/MWh;
PW, jt——风机j在时间段t内的预测发电量值, MW。
风电功率预测误差一般可以分为2种情况: 一是预测风电功率大于实时风电功率; 二是预测风电功率小于实时风电功率。风电功率预测误差可表示为
| $ \varepsilon \%=\frac{P_{\mathrm{W}, j t}-P_{\mathrm{W}, j t}^{\mathrm{r}}}{P_{\mathrm{W}, j t}} \times 100 \% $ | (2) |
式中: PW, jtr——风机j在时间段t内的实际发电量值, MW。
当风力发电的预测值比实际的风力发电值大时, 为了确保系统平衡, 需要提高火电机组的输出值, 火力发电机组的输出值是预测结果和实际结果之间的偏差。当风力发电的预测值比实际的输出值小, 就需要减少火力发电的值或者将风电实际多发的电量废弃, 引发弃风现象。预测值与实际风功率值相差太大或太小, 均可能导致系统运行方式发生变化, 对系统运行产生不利影响; 偏差越大, 影响越大[21]。
为了量化风电预测偏差的影响, 风电预测偏差的影响表现为经济成本的形式。风电预测结果的偏差费用函数为
| $ F_{\mathrm{dh}, t} =C_{\mathrm{dh}}\left(P_{\mathrm{W}, j t}-P_{\mathrm{w}, t}^{\mathrm{r}}\right), P_{\mathrm{W}, j t} \geqslant P_{\mathrm{W}, t}^{\mathrm{r}} $ | (3) |
| $ F_{\mathrm{dl}, t} =C_{\mathrm{dl}}\left(P_{\mathrm{W}, j t}-P_{\mathrm{W}, t}^{\mathrm{r}}\right), P_{\mathrm{W}, j t} \leqslant P_{\mathrm{W}, t}^{\mathrm{r}} $ | (4) |
| $ F_{\mathrm{d}}=\sum\limits_{t=1}^{T}\left(F_{\mathrm{dh}, t}+F_{\mathrm{dl}, t}\right) $ | (5) |
式中: Fdh, t——在时间段t内的高估成本函数;
Cdh——高估风力发电量预测的成本因素, 元/MW;
Fdl, t——在时间段t内的低估成本函数;
Cdl——低估风力发电量预测的成本因素, 元/MW;
Fd——风力发电量高估和低估带来的成本总和。
由于风电出力的随机性, 所以风电的预测输出值往往会出现偏差。为了保证系统的安全稳定, 系统必须增加旋转备用容量。为此, 考虑到风电预测误差造成的成本增加, 引入了基于风电可靠性预测的旋转备用容量成本[22], 公式为
| $ F_{\mathrm{r}}=\sum\limits_{t=1}^{T} C_{\mathrm{r}}\left(1-E_{\mathrm{r}}\right) P_{\mathrm{w}, j t} $ | (6) |
式中: Cr——旋转备用的价格, 元/MW;
Er——每小时第j台风机预测发电量的可靠性。
所以, 风机发电量的成本总和为
| $ F_{\mathrm{w}}=F_{\mathrm{m}}+F_{\mathrm{d}}+F_{\mathrm{r}} $ | (7) |
2.2 火电厂的发电成本
电力系统中火电机组的经济运行特性不同。火电机组的消耗特性在经济运行分析中往往会趋于平稳连续曲线[23]。火电机组的发电成本为
| $ F_{\mathrm{G}}=\sum\limits_{t=1}^{T} \sum\limits_{i=1}^{N}\left(a_{i}+b_{i}+c_{i} P_{\mathrm{G}, i t}^{2}\right) $ | (8) |
式中: ai, bi, ci——第i台火电机组发电成本系数, 元/h, 元/MWh, 元/MW2h;
PG, it——时间段t内火电机组i的输出功率, MW。
3 动态经济调度约束
为保证电源区安全稳定供电, 必须限制系统的技术参数。约束条件主要包括: 最大输出功率约束、输电稳定性约束、热和风功率输出约束和系统备用服务约束等。
3.1 整个系统的功率平衡约束
电力系统中发电厂的发电容量必须满足系统的负荷, 以保证电力系统的正常运行。
| $ \sum\limits_{i=1}^{N} d_{i} P_{\mathrm{G}, t}+P_{\mathrm{w}, t}-P_{\mathrm{d}, t} \geqslant 0 $ | (9) |
式中: di——机组i的状态标识, 当di=1时表示机组在投入运行, di=0时表示机组处于停机状态;
PG, t——在时间段t内所有火电机组的总发电量;
PW, t——在时间段t内的风力发电量;
Pd, t——在时段t内的负荷预测值。
3.2 火电机组运行约束条件
每1台火电机组的发电量的最高和最低的限制为
| $ P_{i}^{\min } \leqslant P_{i} \leqslant P_{i}^{\max } $ | (10) |
式中: Pimin, Pimax——第i台火力发电机组的输出功率的最低和最高功率。
3.3 火电机组爬坡率约束
系统发电量的广泛波动会危及电力系统输入区域的安全, 因此必须限制发电机组单位时间内输出功率的变化幅度。发电机组的爬坡率表示1 h内可以提高或降低发电机出力的大小。
| $ -R_{\text {down }} \leqslant P_{\mathrm{G}, i t}-P_{\mathrm{G}, i(t-1)} \leqslant R_{\mathrm{up}} $ | (11) |
式中: Rdown, Rup——第i台火电机组在1 h内有功功率的减少量和增加量, 一般情况下, Rdown=Rup;
PG, it——时间段t内火电机组i的输出功率, MW;
PG, i(t-1)——时间段t-1内火电机组i的输出功率, MW。
3.4 旋转备用约束
当电力系统运行时, 发电侧和需求侧都可能发生波动。为了保证实时平衡, 应通过增加或降低功率输出来调节电源的输出功率在一定的范围内。因为风力发电只能提供电能, 不具备提供备用的能力, 因此由火电机组提供旋转备用。
| $ \sum\limits_{i=1}^{N} d_{i} P_{\mathrm{G} i}^{\max }-\sum\limits_{i=1}^{N} d_{i} P_{\mathrm{G}, i t}-P_{\mathrm{W}, t} \geqslant S_{\mathrm{up}, t} $ | (12) |
| $ \sum\limits_{i=1}^{N} d_{i} P_{\mathrm{G}, i t}-\sum\limits_{i=1}^{N} d_{i} P_{\mathrm{G} i}^{\min }+P_{\mathrm{W}, t} \geqslant S_{\mathrm{down}, t} $ | (13) |
式中: Sup, t, Sdown, t——确保系统安全的最小正负旋转备用容量;
PGimax——发电机i的最大输出功率, MW;
PGimin——发电机i的最小输出功率, MW。
3.5 风电穿透功率约束
为了确保电能质量, 系统中的风力发电量不能超过一定的值, 为
| $ P_{\mathrm{W}, t} \leqslant \mu P_{1, t} $ | (14) |
式中: μ——系数;
Pl, t——在时间段t内的负荷需求。
式(1)~(14)建立了风电并网的电力系统动态调度模型。该模型考虑了碳排放量分配和风功率的随机性对调度方案的影响, 并以实际风功率作为优化变量之一。在优化调度方案的同时, 实现了风电的最优接入, 模型中使用的系数模拟了实际的电力系统, 保证了本文结果的真实性。
4 碳交易机制的构建
碳交易可以改善风电与火电之间的置换交易, 降低火电厂CO2的排放成本。通过碳交易的价格差异在一定程度上可以获得碳排放收益。同时, 为了低碳发展, 减少火电厂的分发电量, 提高发电区的可再生能源发电比例, 实行绿色贸易证书可以带来超额收益。根据上节提出的碳交易机制, 政府将碳排放权分配给火力发电厂。如果实际排放量小于规定的排放限额, 则剩余碳排放额度可在碳交易市场上销售以获取利润。
4.1 CO2实际排放量
可再生能源风力发电的CO2排放量几乎为零, 可以忽略不计。火电厂CO2排放的主要来源是火电机组, 常规火电机组的碳排放量与机组参数有关, 为
| $ E_{\mathrm{p}}=\sum\limits_{t=1}^{T^{\prime}} \sum\limits_{i=1}^{N} \sigma_{i} P_{\mathrm{G}, i t} T $ | (15) |
式中: σi——机组i的碳排放强度, t/MWh。
4.2 CO2排放分配额度
碳排放额度与不同发电机组的容量成正比。政府分配的初始排放额度为免费。发电单位分配的碳排放限额为
| $ E_{q}=\sum\limits_{t=1}^{T} \eta P_{\mathrm{G}, t} $ | (16) |
式中: η——每单位电量的分配额度, t/MWh。
根据国家发展和改革委员会发布的“区域电网基准排放系数”确定。
4.3 碳排放交易
本文对火电厂碳交易分为2种情况进行了分析。一是当火电厂实际碳排放量大于规定排放限额时, 多余的部分应在碳交易市场上购买, 否则碳排放企业将受到重罚; 二是当火电厂实际碳排放量小于规定排放限额时, 剩余的额度可以在碳交易市场上销售以获取利润。
为了达到最小化系统碳交易成本以及最大化含风电系统的整体收益的目的, 可用式(17)表示, 以达到本文的最终低碳发展的目的。
| $ F_{\mathrm{C}}=C_{\mathrm{P}}\left(E_{\mathrm{p}}-E_{\mathrm{q}}\right) $ | (17) |
式中: FC——碳排放成本;
CP——CO2交易的价格。
FC>0, 代表碳过排放, 火力发电厂需要从碳市场购买一定数量的碳排放物, 这就表示碳排放过量带来的成本; FC < 0, 代表火力发电厂的碳排放在分配的额度内, 多余的排放配额就可以送到碳交易市场售卖, 获取一定的利益。
5 基于改进PSO和GA的动态低碳调度模型
火力和风力发电权置换与碳排放交易机制是优化热力产业结构、降低能源消耗和排放的市场机制。在碳排放交易机制下, 不同机组技术的碳排放参数不同, 发电计划也随之发生变化。在碳交易机制下可实现系统利润最大化。本文研究建立的优化模型, 以最大化火电和风电利润为目的。为了最大限度地降低CO2排放成本、风电成本和发电成本, 动态经济调度目标函数为
| $ F_{\mathrm{T}}=F_{\mathrm{W}}+F_{\mathrm{G}}+F_{\mathrm{C}} $ | (18) |
电力系统经济调度的求解方法可分为2类: 一类是传统的求解方法, 如线性规划方法、非线性规划方法、动态规划、内点法、等微增率等; 一类是现代启发式算法, 如PSO,GA,蚁群算法等神经网络算法。
PSO是一种模仿鸟群社会行为的优化算法, 其中用随机解决方案(称为粒子)群体初始化个体, 群体中的每个粒子代表优化问题的候选解, 如果解是由一组变量组成, 则粒子可以相应为一组解向量。在PSO求解过程中, 每个粒子通过多维搜索空间“飞行”, 根据自己的经验和相邻粒子的经验调整其在搜索空间中的位置。因此, 粒子利用自身及其邻居所遇到的最佳位置, 将自己定位于最佳解决方案, 使用预定义的适应函数来评估每个粒子的性能, 封装了优化问题的特征。在每次迭代中, 每个粒子速度的计算公式为
| $ \begin{aligned} v_{i}(t+1)=& w v_{i}+c_{1} r_{1}\left(p_{i d}-x_{i}(t)\right)+\\ & c_{2} r_{2}\left(p_{\mathrm{gd}}-x_{i}(t)\right) \end{aligned} $ | (19) |
式中: w——惯性权重;
c1, c2——加速度常数;
r1, r2——[0, 1]范围内的2个随机数;
xi(t)——粒子的当前位置;
pid——粒子当前的最优解;
pgd——所有粒子已经达到的最优解。
计算出速度后, 再计算每个粒子的新位置, 公式为
| $ x_{i}(t+1)=x_{i}(t)+v_{i}(t+1) $ | (20) |
PSO算法执行上述更新方程的重复应用, 直到超过指定的迭代次数, 或者直到速度更新接近于零。
GA算法已成功应用于优化设计、模糊逻辑控制、神经网络和调度中。对于特定问题, GA算法将解编码为单个染色体, 然后确定代表问题解的一个子代群体, 搜索空间定义为每个可行解由不同染色体表示的解空间。在搜索开始前, 从搜索空间随机选择一组染色体以形成初始群体, 接下来通过计算, 基于其通过特定目标函数测量的适合度选择个体。
将GA选择算子, 如选择、变异、交叉等应用于获得新一代染色体。重复这个过程直到终止条件达到, 最后一代的最佳染色体作为最终的解。
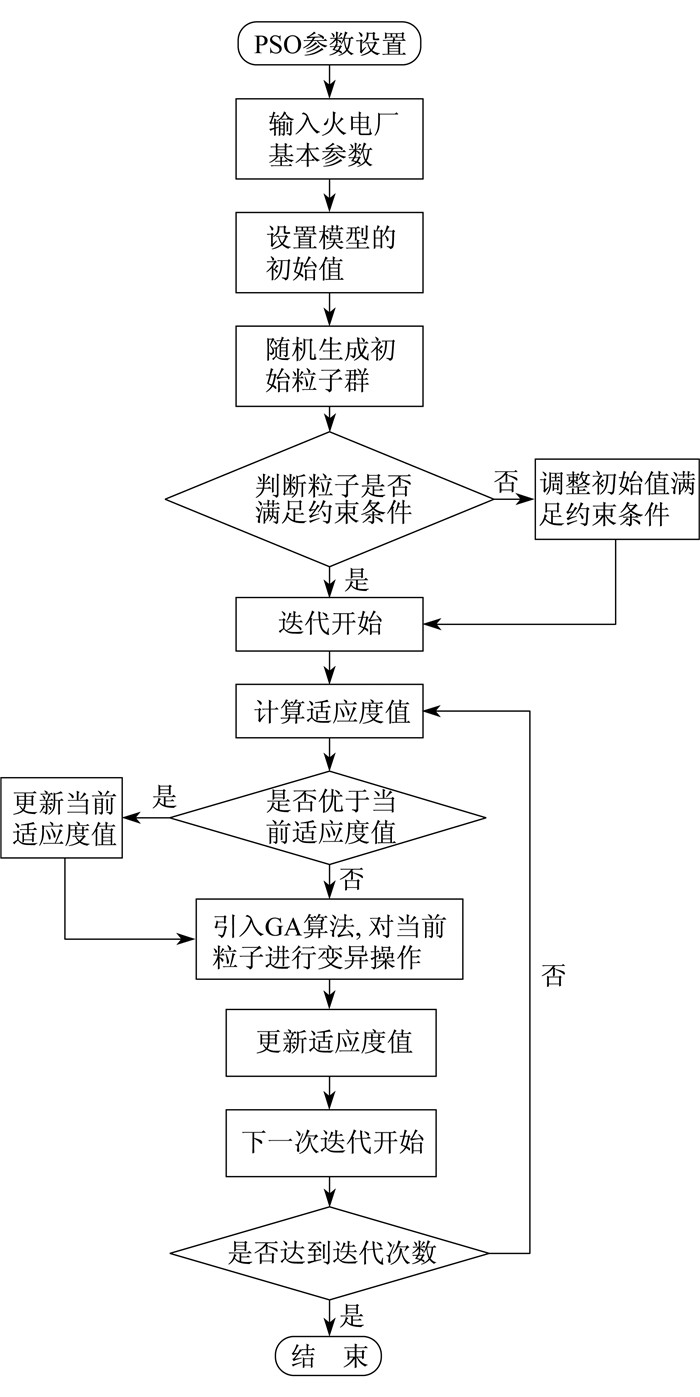
GA算法与PSO算法均基于群体叠代。与PSO算法中粒子在解空间追随最优粒子进行搜索不同, GA算法拥有典型的交叉及变异, 能将每一代个体按照一定的程度进行交叉变异, 将结果较差的子代淘汰。本研究使用GA算法的遗传变异功能, 将粒子群每一代的粒子在一定的程度上进行交叉, 更新粒子在搜索空间的位置。在计算每一代粒子的适应度值后, 根据迭代次数的不同, 加入不同权重的罚函数。改进的PSO-GA算法流程如图 2所示。
6 实验过程及结果
6.1 实验数据及环境
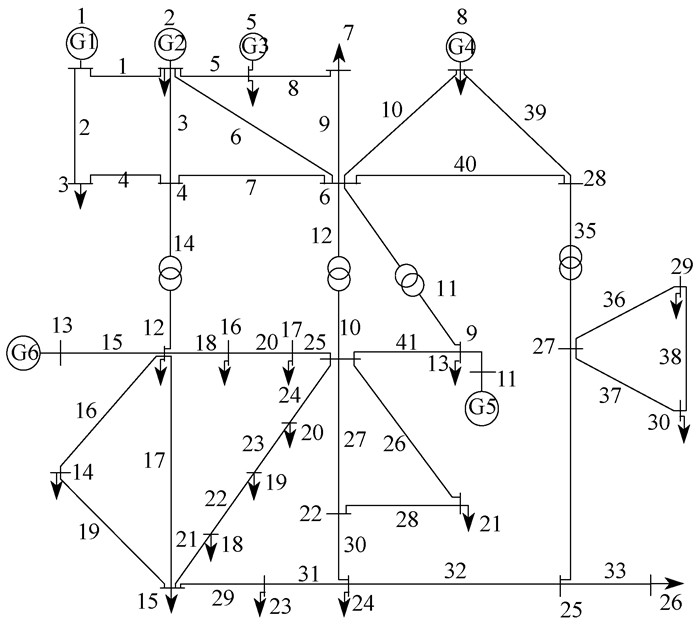
本文以IEEE-30节点系统为例进行仿真分析, 系统接线如图 3所示。
该系统有6台发电机, 成本系数和其他相关参数如表 1所示。
表 1
火电机组参数
| 机组 | PGimax | PGimin | ai | bi | ci | Rup | Rdown | σi |
| G1 | 200 | 50 | 0 | 200 | 75 | 5.000 | 5.000 | 0.88 |
| G2 | 80 | 20 | 0 | 175 | 350 | 2.000 | 2.000 | 0.96 |
| G3 | 50 | 15 | 0 | 100 | 1 250 | 1.250 | 1.250 | 1.12 |
| G4 | 35 | 10 | 0 | 200 | 167 | 0.875 | 0.875 | 0.40 |
| G5 | 30 | 10 | 0 | 150 | 500 | 0.750 | 0.750 | 0.98 |
| G6 | 40 | 12 | 0 | 200 | 500 | 1.000 | 1.000 | 0.42 |
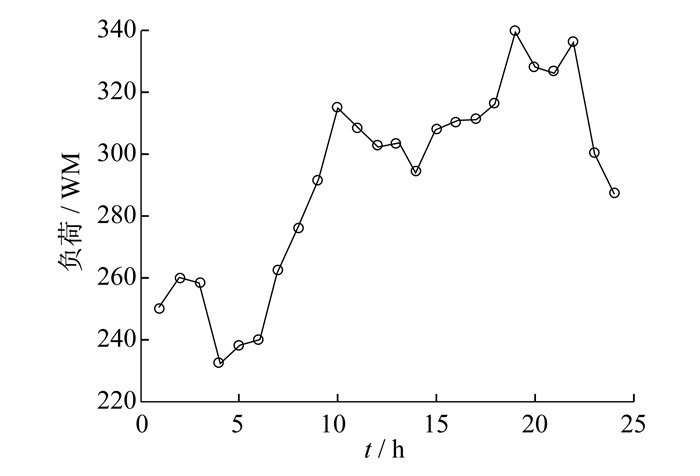
将上文中风电功率预测结果通过节点16接入系统, 风电场容量为150 MW。选取一日为一调度周期, 每一个调度周期分为24 h, 系统负荷需求预测数据如图 4所示。
在实验中所使用的参数值如表 1所示。每单位电量的分配额度η为0.798/MWh, 风力发电的置信水平Er为0.85。负荷值的正、负旋转备用容量值为5%, 旋转备用的价格Cr为200元/MW。运行和维护成本是根据实际运行和维护风电成本Cm确定的, 即55元/MWh。风电的高估mdh和低估mdl的成本因素的成本系数估分别为125元/MW和230元/MW。
6.2 实验结果
为了研究本文低碳经济调度的优势与特性, 分别对以下2种场景下不同的调度结果和经济性进行了讨论。
场景1:以降低火力发电成本的经济性为目标, 使用传统的调度模型, 将火电机组最小运行成本作为目标函数, 碳排放的交易成本不包含在内。
场景2:基于本文提出的低碳经济调度模型, 需要满足风力发电成本、火力发电成本和碳排放交易成本的总和最小。
在这2种场景下, 碳交易价格为150元/t。以一日24个时段作为一个调度周期。2种场景下的动态经济调度如表 2所示。
表 2
动态经济调度运行结果
| 场景 | 火力发电量 | 风力发电量 | 风力发电成本 | 火力发电成本 | 碳排放成本 | 发电成本总和 | |
| kWh | 元 | ||||||
| 1 | 7.126×103 | 1.259 0×103 | 4.042×105 | 1.371×106 | 1.375×104 | 1.789×106 | |
| 2 | 7.352×103 | 1.044 1×103 | 3.294×105 | 1.414×106 | 1.179×104 | 1.759×106 | |
在场景1中, 目标函数是最小化火力发电成本, 所以从风力发电量和火力发电量的结果来看, 场景1的火力机组发电的成本比场景2的火力发电成本低, 对应的火力发电机组也比场景2的少。由于场景1减少了火力发电量, 为了满足系统负荷的平衡, 所以相对应的风力发电量就会多于场景2, 从而带来更高的风力发电成本。但是对比两种场景下的碳排放成本, 可以看出场景2的碳排放成本更低, 这是因为场景1是以火电机组的发电成本最小为目标函数, 所以在发电时, 优先让发电成本较小的机组发电, 但是较小的发电成本机组就具有较高的碳排放系数, 进一步导致了场景1的碳排放成本高于场景2。由于场景2是以火电、风电和碳排放三者总的发电成本为目标函数, 使得场景2总的发电成本低于场景1, 从而验证了本文提出的碳排放模型的经济性优于传统的经济调度模型。
7 结语
风电的大规模接入和碳交易的引入, 对传统的调度模型产生了影响。由于传统的调度模型仅仅基于风电和火电的组合发电成本, 并未考虑到低碳因素的影响, 因此其机组的开停机顺序更注重的是调度经济性。碳交易的引入使得机组组合方式不能再忽略碳排放成本这一因素。本文基于GA算法和PSO算法的改进算法求解机组的出力, 并且通过3种调度模式的对比, 讨论了碳交易引入对调度成本的影响、不同的碳权比重对于调度结果的影响及碳交易价格对于调度成本的影响。最终的算例分析证明了机组组合的优越性。
参考文献
-
[1]周玮, 彭昱, 孙辉, 等. 含风电场的电力系统动态经济调度[J]. 中国电机工程学报, 2009, 29(25): 13-18. DOI:10.3321/j.issn:0258-8013.2009.25.003
-
[2]袁铁江, 晁勤, 吐尔逊, 等. 电力市场环境下含风电机组的环境经济调度模型及仿真[J]. 电网技术, 2009, 33(6): 13-18. DOI:10.3969/j.issn.1674-0629.2009.06.003
-
[3]CHEN X Y, KANG C Q, CHEN M J. Short term probabilistic prediction of the magnitude and timing of extreme load[J]. Proc CSEE, 2011, 31(22): 64-72.
-
[4]盛四清, 孙晓霞. 利用风蓄联合削峰的电力系统经济调度[J]. 电网技术, 2014, 38(9): 2484-2489.
-
[5]HOLGER H, WERNER R. Scenario reduction algorithms in stochastic programming[J]. Computational Optimization and Applications, 2003, 24: 187-206. DOI:10.1023/A:1021805924152
-
[6]张歩涵, 邵剑, 吴小珊, 等. 基于场景树和机会约束规划的含风电场电力系统机组组合[J]. 电力系统保护与控制, 2013, 41(1): 127-135.
-
[7]张晓辉, 闫柯柯, 卢志刚, 等. 基于场景概率的含风电系统多目标低碳经济调度[J]. 电网技术, 2014, 38(7): 1835-1841.
-
[8]LI L, WANG Y M, LIU Y Q. Impact of wake effect on wind power prediction[C]//2nd IET Renew Power Generation Conference. Beijing, China, 2013: 1-4.
-
[9]BAGHERI A, MONSEF H, LESANI H. Integrated distribution network expansion planning incorporating distributed generation considering uncertainties, reliability, and operational conditions[J]. Int J Electr Power Energy Syst, 2015, 73: 56-70. DOI:10.1016/j.ijepes.2015.03.010
-
[10]CHEN S P, DONG R, LUO X L. Analysis of 30 Cases of MATLAB Neural Network[M]. Beijing: Beihang University Press, 2010: 73-74.
-
[11]ZHOU W, SUN H, GU H. Dynamic economic dispatch of wind integrated power systems based on risk reserve constraints[J]. Proceedings of the CSEE, 2012, 32(1): 47-55.
-
[12]程昊汝. 我国碳排放权机制设计的研究[D]. 上海: 华东师范大学, 2011.
-
[13]袁铁江, 晁勤, 吐尔逊, 等. 大规模风电并网电力系统动态清洁经济优化调度的建模[J]. 中国电机工程学报, 2010, 30(31): 7-13.
-
[14]WANG C X, QIAO Y, LU Z X, et al. Day-ahead dispatch mode for wind-thermal power system in low-carbon economy[J]. Automation of Electric Power Systems, 2011, 35(22): 111-117.
-
[15]YUAN T J, CHAO Q, TOERXUN Y. Optimized economic and environment friendly dispatching modeling for large-scale wind power integration[J]. Proceedings of the CSEE, 2010, 30(31): 7-13.
-
[16]DONG X T, YAN Z, FENG D H, et al. Power system economic dispatch considering penalty cost of wind farm output[J]. Power System Technology, 2012, 36(8): 76-80.
-
[17]LEE J C, LIN W M, LIAO G C, et al. Quantum genetic algorithm for dynamic economic dispatch with valve-point effects and including wind power system[J]. Electrical Power and Energy Systems, 2011, 33(2): 189-197. DOI:10.1016/j.ijepes.2010.08.014
-
[18]WANG L F, SINGH C. Tradeoff between risk and cost in economic dispatch including wind power penetration using particle swarm optimization[C]//International Conference on Power System Technology. Chongqing, China, 2006: 1-7.
-
[19]国家发展和改革委员会应对气候变化司. 关于公布2012年中国区域电网基准线排放因子的公告[EB/OL]. (2020-05-07)[2012-01-13]. http://cdm.ccchina.gov.cn/Website/CDM/UpFile/File2975.pdf.
-
[20]ROMBAUTS Y, DELARUE E, D'HAESELEERS W. Optimal portfolio-theory-based allocation of wind power: taking into account cross-border transmission-capacity constraints[J]. Renew Energy, 2011, 36(9): 2374-2387. DOI:10.1016/j.renene.2011.02.010
-
[21]ZHANG L Y, YE T L, XIN Y Z, et al. Problems and measures of power grid accommodating large scale wind power[J]. Proc CSEE, 2010, 30(25): 1-9.
-
[22]WANG N B, WANG J D, HE S E. Cross-border accommodation method and transmission scheme of Jiuquan wind power[J]. Autom Electr Power Syst, 2011, 35(22): 82-89.
-
[23]XU W, YANG Y L, LI Z G, et al. Participation mode of large-scale Jiuquan wind power farm in Gansu province to electricity market and its utilization scheme[J]. Power Syst Tech, 2010, 34(6): 71-77.