|
|
|
发布时间: 2022-02-28 |
清洁安全发电 |
|
|
|
收稿日期: 2021-03-23
基金项目: 国家自然科学基金(51806135)
中图法分类号: TP277
文献标识码: A
文章编号: 2096-8299(2022)01-0029-06
|
摘要
为了实现滚动轴承变工况运行下仍能进行有效的故障诊断, 提出了一种基于二维卷积神经网络的滚动轴承变工况故障诊断方法。该方法将原始信号以及运行载荷这一工况变量作为输入信号, 无需人工提取特征向量, 减少特征提取过程中的损失, 实现端到端检测, 并将该方法与传统卷积神经网络模型进行了实验对比。结果表明, 相较于传统卷积神经网络, 该方法在故障的识别准确率和诊断的实时性上都有很大程度的提升。
关键词
二维卷积; 神经网络; 变工况; 故障诊断; 端到端检测
Abstract
In order to effectively diagnose the rolling bearing under variable operating conditions, a fault diagnosis method based on two-dimensional convolutional neural network for rolling bearing variable operating conditions is proposed.By using the original signal and operating load as the input signal, no manual operation is required.The feature vector is extracted to reduce the loss in the process of feature extraction and realize end-to-end detection, and is compared with the traditional convolutional network model.The results show that compared with the traditional convolutional neural network, this method has greatly improved the accuracy of fault recognition and the real-time performance of the diagnosis.
Key words
two-dimensional convolution; neural network; variable conditions; fault diagnosis; end-to-end detection
滚动轴承作为旋转机械设备(如涡轮机、发电机等)的重要零部件, 由于其本身的磨损、变形等损伤所引起的设备故障占机械设备故障的50%[1]。在设备实时运行中, 实时故障诊断可以在最大程度上减少重大事故的发生[2]。轴承故障诊断方法的基本原理就是从轴承设备端所采集到的数据中提取信号的特征并且进行分类, 从而实现对设备的故障检测。
2016年之前, 基于应用统计学的传统机器学习方法, 例如基于支持向量机的风险最小化原理的故障诊断方法[3]、基于人工神经网络的故障诊断系统[4], 作为当时极其有效且流行的方法, 得到了广泛的应用[5]。
近年来, 随着机械设备的监测传感器所采集的数据变得越来越多样化、抽象化和复杂化[6]。以往传统故障诊断方法在时效性和识别准确率方面差强人意, 但基于深度学习[7]的神经网络, 例如深度置信网络、堆叠稀疏自编码器[8]和卷积神经网络, 有着众多隐含层, 具有很强的自主学习能力, 在复杂数据集上有很大的优势[9]。其中, 卷积神经网络可以通过逐层学习故障信号, 自适应提取特征值[10-12], 并且随着模型网络深度的提升, 特征学习和故障分类的效果也会相应地提高, 但在时效性上可能会略有损失[13]。卷积神经网络以原始信号作为输入, 不需要进行特征提取, 从而达到端到端的故障诊断, 不需要额外进行去噪声处理, 解决了工作噪声对故障识别的影响[14]。卷积神经网络在故障识别方面可以极大地减少人为提取信号特征的步骤, 但是以往的卷积网络故障诊断模型在滚动轴承的运行载荷发生改变的情况下, 故障诊断的准确率与实时性并不理想。
因此, 本文提出了一种在轴承运行载荷发生改变时, 可以对其故障进行准确且有效诊断的二维卷积神经网络模型。该模型可以实现对故障进行端到端检测, 仅需输入原始数据, 无需人工提取特征向量, 减少了特征提取过程中的损失, 提高了模型诊断的准确性, 整个故障诊断过程都是在模型当中进行自适应学习、训练和诊断。该模型的数据预处理方法在原始一维信号转化为二维信号时, 无需额外定义任何参数, 减少了以往专家经验对数据信号转化过程的损失。另外, 构建模型时, 可以使特征信号在梯度下降后自适应优化权重参数, 增加故障诊断的识别准确率。最后, 根据多次试验数据和结果证明该故障诊断模型的有效性和准确性。
1 二维卷积神经网络故障诊断模型
1.1 变工况下的二维卷积神经网络构造
在一维卷积神经网络中, 往往需要至少1 024或2 048个数据点[15]来完成特征提取和数据识别, 使得其在故障诊断的时效性方面略有不足, 而且在运行载荷发生变化的变工况状态下, 无法进行有效且准确的诊断。
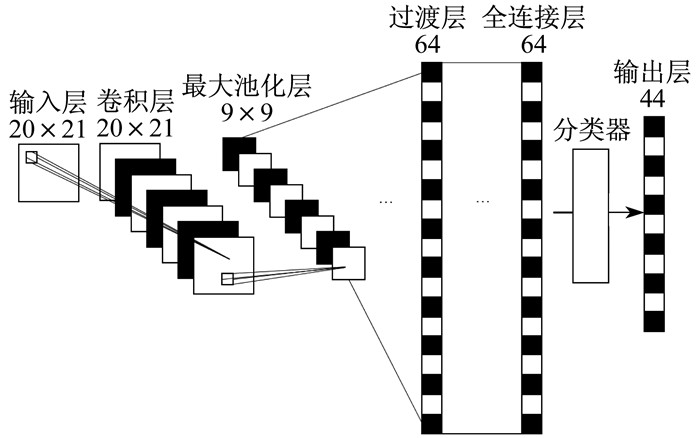
相对于普通一维卷积神经网络, 二维卷积神经网络可以通过较少的样本量全面反映滚动轴承的故障状态, 而且耗时也会减少。为了在轴承的运行载荷发生改变时对轴承故障进行有效及准确的诊断, 对变工况下的二维卷积神经网络进行构造。二维卷积神经网络结构如图 1所示。
该故障诊断模型仅需要420个数据点作为一个样本点, 大大缩短了故障诊断的时间。将轴承工况变量作为输入信号, 包含在420个数据点当中, 增加其对变工况故障诊断的有效性和准确性。在模型中设置5层卷积层, 最后3层卷积与池化层逐步完善特征信号的提取, 其中输入层的尺寸为20×21。为了提取数据集中的特征信号, 降低信号维度, 模型中5层卷积层与3层池化层互相交替, 在输入层与第1层卷积层之间的卷积核大小设置为5×5×1, 在自适应提取特征信号的同时降低维度, 减少模型的学习和训练时间, 第2层卷积层中的卷积核大小为5×5×32, 从第4层卷积层开始, 模型当中的卷积核从第3层卷积层中的3×3×32变成为3×3×64;3层池化层的尺寸与步长相同, 分别为3×3和2;在进入全连接层和最后一层激活函数Softmax之前, 通过过渡层, 形状(4, 4, 64)的输出被展平为形状64的向量, 第11层为全连接层, 其中包含了64个节点; 通过模型最后一层的Softmax分类器完成对变工况下4种故障类型、3种严重程度共44种故障类型的分类。
本文构建的二维卷积神经网络模型的结构参数如表 1所示。
表 1
变工况下模型结构参数
| 层数 | 基本层类型 | 通道数 | 矩阵大小 |
| 1 | 输入层 | 1 | 20×21 |
| 2 | 卷积层1 | 32 | 20×21 |
| 3 | 池化层1 | 32 | 9×9 |
| 4 | 卷积层2 | 32 | 9×9 |
| 5 | 池化层2 | 32 | 4×4 |
| 6 | 卷积层3 | 64 | 4×4 |
| 7 | 卷积层4 | 64 | 4×4 |
| 8 | 卷积层5 | 64 | 4×4 |
| 9 | 池化层3 | 64 | 1×1 |
| 10 | 过渡层 | 1 | 64 |
| 11 | 全连接层 | 1 | 64 |
| 12 | Softmax分类器 | 1 | 44 |
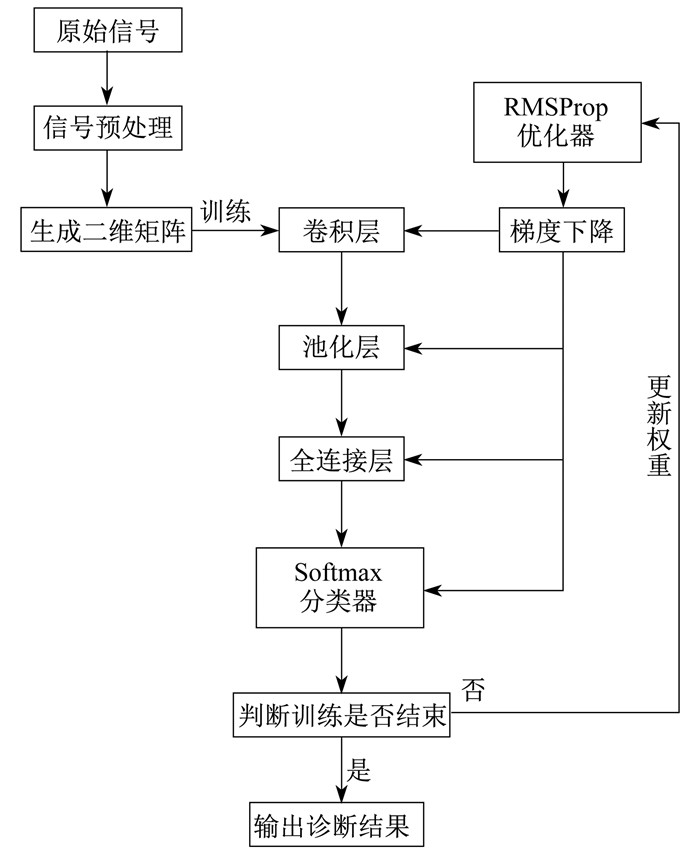
1.2 模型训练
模型采用RMSProp优化器。其数学模型可表达为
| $ {\mathit{\boldsymbol{v}}_t} = \mathit{\rho }{\mathit{\boldsymbol{v}}_{t - 1}} + (1 - \mathit{\rho })\mathit{\boldsymbol{g}}_t^2 $ | (1) |
式中: vt——梯度平方在t时刻的指数平均值;
t——时刻;
ρ——衰减速率;
gt——参数更新之后在各个梯度方向上的投影向量。
RMSProp优化算法中的参数优化公式如下
| $ {\mathit{\boldsymbol{\omega }}_{t + 1}} = {\mathit{\boldsymbol{\omega }}_t} + \Delta {\mathit{\boldsymbol{\omega }}_t} $ | (2) |
| $ \Delta {\mathit{\boldsymbol{\omega }}_t} = - \frac{\mathit{\eta }}{{\sqrt {{v_t} +\epsilon } }}{\mathit{\boldsymbol{g}}_t} $ | (3) |
式中: ωt——t时刻的原始步长;
Δωt——更新过后的步长变量;
η——初始学习率;
等式右边的负号表示它与梯度移动的方向相反。RMSProp算法与一般梯度下降算法最大的不同就是把学习率这个超参数从原来的标量变成了一个向量。
通过消除梯度下降时的摆动从而加速梯度下降的过程, 就能设置较大的学习率, 使得训练加快[16]。为了防止模型运行过程中出现过拟合, 并加强神经网络的泛化能力, 在全连接层后加入一个Dropout层, 采用Dropout正则化, 将其参数大小设置为0.5, 以此加强网络节点的鲁棒性。该二维卷积网络模型可以实现对于故障端到端的诊断, 即从原始信号到故障识别, 同时完成自适应学习, 不需要定义额外参数。网络模型的流程图如图 2所示。
2 实验验证
2.1 数据集介绍
本文使用的数据集来自美国凯斯西储大学轴承数据中心在4种载荷情况下所收集到的数据。该数据集是当前轴承振动信号处理、故障诊断方面应用最为广泛的标准数据集[17-18]。
在12 kHz采样频率下, 电机载荷分别为0 W, 735 W, 1 471 W, 2 206 W, 电机近似转速为1 797 r/min时, 采用了4组内圈故障、滚动体故障和外圈损伤点在6点方向上的10类故障数据集和1类正常数据集。故障分类如表 2所示。
表 2
故障分类
| 电机载荷/W | 故障直径/mm | 内圈故障数据集 | 滚动体故障数据集 | 外圈故障数据集 |
| 0 | 0.177 8 | IR007 | B007 | OR007@6 |
| 0 | 0.355 6 | IR014 | 无 | OR014@6 |
| 0 | 0.533 4 | IR021 | B021 | OR021@6 |
| 0 | 0.711 2 | IR028 | B028 | 无 |
| 735 | 0.177 8 | IR007_1 | B007_1 | OR007@6_1 |
| 735 | 0.355 6 | IR014_1 | 无 | OR014@6_1 |
| 735 | 0.533 4 | IR021_1 | B021_1 | OR021@6_1 |
| 735 | 0.711 2 | IR028_1 | B028_1 | 无 |
| 1 471 | 0.177 8 | IR007_2 | B007_2 | OR007@6_2 |
| 1 471 | 0.355 6 | IR014_2 | 无 | OR014@6_2 |
| 1 471 | 0.533 4 | IR021_2 | B021_2 | OR021@6_2 |
| 1 471 | 0.711 2 | IR028_2 | B028_2 | 无 |
| 2 206 | 0.177 8 | IR007_3 | B007_3 | OR007@6_3 |
| 2 206 | 0.355 6 | IR014_3 | 无 | OR014@6_3 |
| 2 206 | 0.533 4 | IR021_3 | B021_3 | OR021@6_3 |
| 2 206 | 0.711 2 | IR028_3 | B028_3 | 无 |
2.2 变工况下的数据预处理
由于本文所构建的故障诊断模型是二维卷积网络模型, 所以需要将原始的一维数据集进行二维转化处理。首先, 对44类原始信号采集400个一维原始数据作为一个样本, 并将工况变量加入样本信号中, 共计420个数据点, 采集300个样本; 由于原始数据是一维数据, 需要将44类数据集通过reshape函数将其转化为二维矩阵, 并将数据集打乱; 最后, 将标签转化为一位有效编码, 即每一次有且仅有一种状态存在。
2.3 变工况下的模型测试
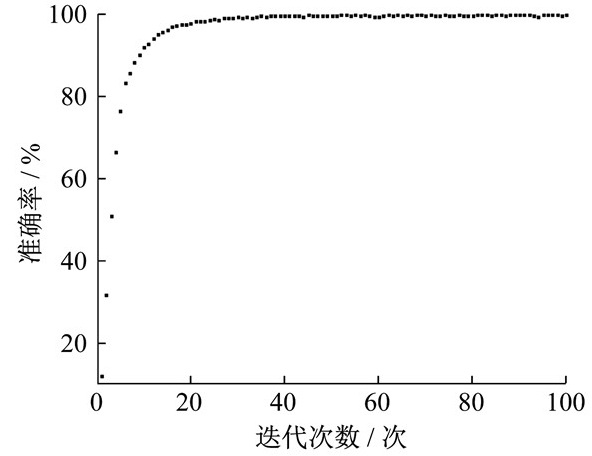
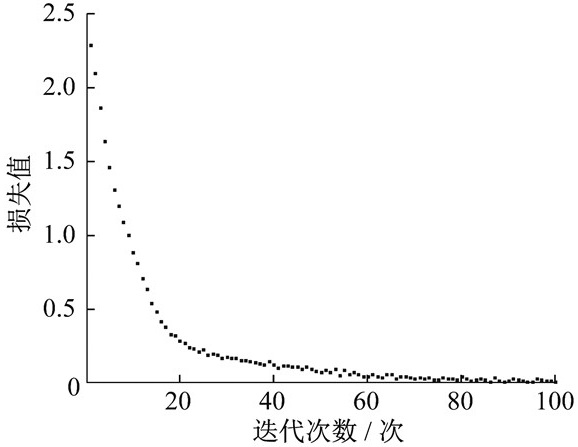
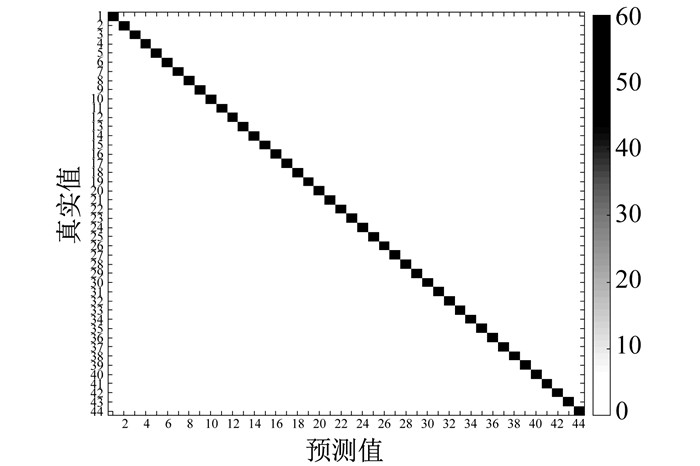
通过数据预处理, 所得到的训练集和测试集样本数据总数量为13 200, 根据实验需要将其按照一定比例随机分配。实验测试采用基于Tensor Flow深度学习架构, 运行环境为Windows 7, 处理器采用的是英特尔公司的i7-4720HQ。将300个样本按照4∶1的比例随机分成训练集和测试集的情况下, 在变工况下对该模型进行100次迭代模拟实验, 实验的训练准确率、损失曲线及可视化的混淆矩阵如图 3、图 4、图 5所示。其中: 训练准确率是指在训练过程中模型的成功率; 损失曲线中的损失值代表了预测值和实际值的相似程度, 损失值越小, 表示相似程度越高; 混淆矩阵是以矩阵形式将模型的故障诊断结果进行汇总表示, 矩阵中的行表示预测值, 列表示真实值, 对角线上的值越高表示诊断结果越好。
模型的诊断结果如表 3所示。模型测试耗时466 s, 单个诊断算列时间约为598 μs, 由于选取的420个数据点少于传统一维卷积神经网络所采用的1 024个, 实验耗时大大减少。由于通过5层卷积和3层池化的特征提取, 基于较少的训练样本, 经过Python软件模拟得到轴承故障诊断的识别准确率可达99.6%, 损失值维持在2.3%。测试集样本数为60, 通过图 5和表 3的模型诊断结果可以看出, 在60次的故障识别中, 其中载荷为735 W时的内圈故障、载荷为735 W时的外圈故障, 载荷为1 471W时的滚动体故障分别有1次未能识别, 其余均正确识别。
表 3
故障诊断结果
| 类别标签 | 误诊样本数目 | 类别标签 | 误诊样本数目 | 类别标签 | 误诊样本数目 | 类别标签 | 误诊样本数目 | |||
| 1 | 0 | 12 | 0 | 23 | 0 | 34 | 0 | |||
| 2 | 0 | 13 | 1 | 24 | 0 | 35 | 0 | |||
| 3 | 0 | 14 | 0 | 25 | 0 | 36 | 0 | |||
| 4 | 0 | 15 | 0 | 26 | 0 | 37 | 0 | |||
| 5 | 0 | 16 | 0 | 27 | 0 | 38 | 0 | |||
| 6 | 0 | 17 | 0 | 28 | 0 | 39 | 0 | |||
| 7 | 0 | 18 | 0 | 29 | 0 | 40 | 0 | |||
| 8 | 0 | 19 | 0 | 30 | 1 | 41 | 0 | |||
| 9 | 0 | 20 | 0 | 31 | 0 | 42 | 0 | |||
| 10 | 0 | 21 | 0 | 32 | 0 | 43 | 0 | |||
| 11 | 0 | 22 | 1 | 33 | 0 | 44 | 0 |
随着迭代次数的增加, 准确率与损失值在迭代次数为40之后趋于平稳, 变化幅度不超过千分之一, 基本可以忽略。在变工况下对该模型进行40次迭代模拟, 模型测试耗时299 s, 单个诊断算列时间约为598 μs, 轴承故障诊断的识别准确率为99.7%, 损失维持在2.4%。与图 3和图 4的结果相符。
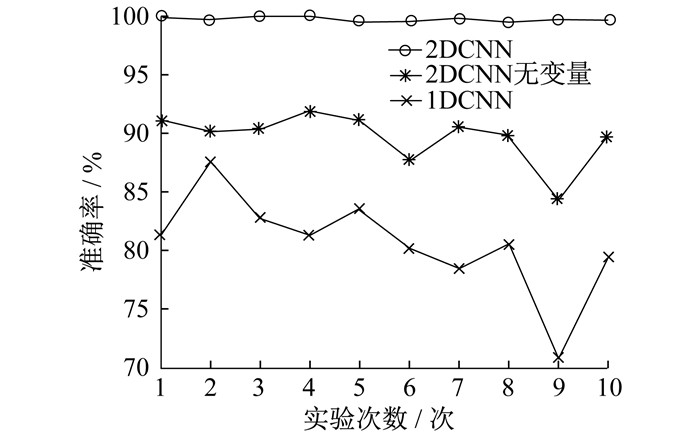
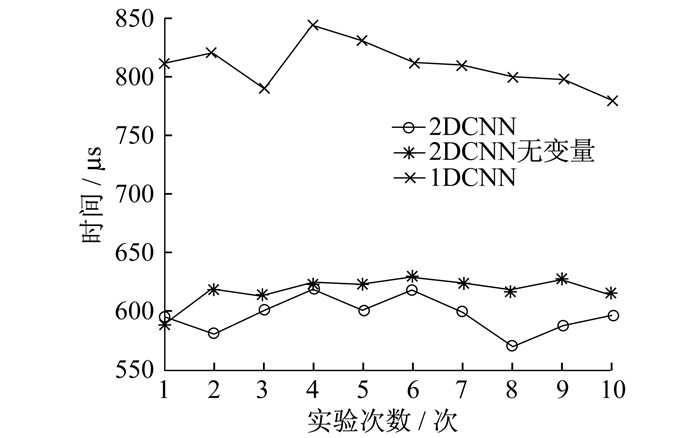
同时将本文所提的变工况下二维卷积神经网络(2DCNN)与传统一维卷积神经网络(1DCNN)、未将工况变量作为输入信号的二维神经卷积网络(2DCNN无变量)进行10次轴承故障诊断的实验对比。将信号直接输入到传统一维卷积神经网络和未将工况变量加入样本信号的二维卷积神经网络中, 样本同样包含420个数据点, 模型的结构为表 2所示的12层, 进行40次迭代。识别准确率与实验耗时的对比情况如图 6和图 7所示。实验数据对比如表 4所示。
表 4
实验数据对比
| 实验次数 | 2DCNN | 2DCNN无变量 | 1DCNN | |||||
| 识别准确率/% | 实验耗时/μs | 识别准确率/% | 实验耗时/μs | 识别准确率/% | 实验耗时/μs | |||
| 1 | 99.92 | 597 | 91.24 | 590 | 81.33 | 810 | ||
| 2 | 99.64 | 582 | 90.16 | 620 | 87.54 | 820 | ||
| 3 | 99.89 | 602 | 90.42 | 614 | 82.80 | 790 | ||
| 4 | 99.96 | 620 | 91.93 | 625 | 81.36 | 844 | ||
| 5 | 99.51 | 601 | 91.10 | 624 | 83.60 | 831 | ||
| 6 | 99.62 | 619 | 87.69 | 630 | 80.19 | 813 | ||
| 7 | 99.66 | 600 | 90.57 | 626 | 78.56 | 810 | ||
| 8 | 99.43 | 571 | 89.85 | 618 | 80.57 | 800 | ||
| 9 | 99.67 | 588 | 84.32 | 628 | 70.95 | 799 | ||
| 10 | 99.56 | 597 | 89.85 | 617 | 79.55 | 780 | ||
通过图 6和图 7可以看出: 一维卷积神经网络在迭代次数和样本容量较小的情况下, 无法完成对多工况、多故障的有效诊断, 在40次的迭代后, 故障诊断的识别准确率仅为70%~88%;但在另外两种二维卷积神经网络模型中, 在相同的迭代次数和样本量情况下, 故障诊断的识别准确分别在99%和90%左右, 均高于一维卷积神经网络; 在故障诊断的时间方面, 相同参数的情况下, 一维卷积神经网络的单个诊断算列的识别时间远远多于另外两种二维卷积神经网络模型, 均超过780 μs。
通过对比实验结果得出, 在较少的迭代次数和样本量的情况下, 本文所提方法在变工况下的识别准确率和故障诊断识别时间上都更有优势。
3 结论
本文提出了一种适用于轴承运行载荷发生改变时, 可以对其故障进行准确且有效诊断的二维卷积神经网络模型。通过变工况的模拟实验, 证明了该模型的有效性以及可行性, 并得出了以下结论。
(1) 本文原始一维信号的处理与转化方式更能完整且有效地保留轴承故障的特征信号, 无需额外定义任何参数, 尽量消除了专家经验所带来的影响, 提高了模型的识别准确率。
(2) 本文提出的变工况下二维卷积神经网络在轴承载荷发生改变的情况下, 实现了对44种故障类型及其严重程度的端到端故障诊断, 轴承故障诊断的识别准确率达到了99.6%。
(3) 本文所提方法模型测试总耗时为466 s, 单个诊断算列时间约为598 μs, 模型的故障识别准确率和诊断的实时性均优于传统卷积神经网络。
参考文献
-
[1]徐文学, 夏懿, 张德祥. 基于稠密卷积网络的轴承故障诊断[J]. 噪声与振动控制, 2020, 40(4): 80-86. DOI:10.3969/j.issn.1006-1355.2020.04.015
-
[2]XU L, CHATTERTON S, PENNACCHI P. Rolling element bearing diagnosis based on singular value decomposition and composite squared envelope spectrum[J]. Mechanical Systems and Signal Processing, 2021, 148: 107174. DOI:10.1016/j.ymssp.2020.107174
-
[3]吴春光, 王建朝, 化麒. 基于NSP和SVM的滚动轴承故障诊断方法[J]. 轴承, 2016(12): 39-42. DOI:10.3969/j.issn.1000-3762.2016.12.011
-
[4]李莉. 采煤机故障分析与诊断探讨[J]. 机械管理开发, 2016, 31(11): 63-65.
-
[5]LAI Z H, WANG S B, ZHANG G Q, et al. Rolling bearing fault diagnosis based on adaptive multiparameter-adjusting bistable stochastic resonance[J]. Shock and Vibration, 2020(9): 1-15.
-
[6]李恒, 张氢, 秦仙蓉, 等. 基于短时傅里叶变换和卷积神经网络的轴承故障诊断方法[J]. 振动与冲击, 2018, 37(19): 124-131.
-
[7]TANG S H, SHEN C Q, WANG D, et al. Adaptive deep feature learning network with Nesterov momentum and its application to rotating machinery fault diagnosis[J]. Neurocomputing, 2018, 305: 1-14. DOI:10.1016/j.neucom.2018.04.048
-
[8]史光宇, 徐健, 杨强. 基于卷积神经网络的风电机组轴承机械故障智能诊断方法[J]. 华北电力大学学报(自然科学版), 2020, 47(4): 71-79. DOI:10.3969/j.ISSN.1007-2691.2020.04.09
-
[9]张西宁, 郭清林, 刘书语. 深度学习技术及其故障诊断应用分析与展望[J]. 西安交通大学学报, 2020(12): 1-13.
-
[10]GUO X J, CHEN L, SHEN C Q. Hierarchical adaptive deep convolution neural network and its application to bearing fault diagnosis[J]. Measurement, 2016, 93: 490-502. DOI:10.1016/j.measurement.2016.07.054
-
[11]ZAHEDINASAB R, MOHSENI H. Neuroevolutionary based convolutional neural network with adaptive activation functions[J]. Neurocomputing, 2020, 381: 306-313. DOI:10.1016/j.neucom.2019.11.090
-
[12]何成兵, 王润泽, 张霄翔. 基于改进一维卷积神经网络的汽轮发电机组轴系扭振模态参数辨识[J]. 中国电机工程学报, 2020, 40(16): 1-9.
-
[13]周奇才, 刘星辰, 赵烔, 等. 旋转机械一维深度卷积神经网络故障诊断研究[J]. 振动与冲击, 2018, 37(23): 31-37.
-
[14]ZHANG W, LI C H, PENG G L, et al. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load[J]. Mechanical Systems and Signal Processing, 2018, 100: 439-453. DOI:10.1016/j.ymssp.2017.06.022
-
[15]应雨龙, 李靖超, 柴萍萍, 等. 基于多特征提取的滚动轴承故障诊断方法[J]. 上海电力学院学报, 2018, 34(5): 413-421. DOI:10.3969/j.issn.1006-4729.2018.05.001
-
[16]JUN S H, BYEOL L E, JOON J H, et al. Evaluation of classification and accuracy in chest X-ray images using deep learning with convolution neural network[J]. Journal of the Korean Society of Radiology, 2020, 14(1): 39-44.
-
[17]LI X, YANG Y, PAN H Y, et al. A novel deep stacking least squares support vector machine for rolling bearing fault diagnosis[J]. Computers in Industry, 2019, 110: 36-47. DOI:10.1016/j.compind.2019.05.005
-
[18]YING Y L, LI J C, CHEN Z M, et al. Study on rolling bearing on-line reliability analysis based on vibration information processing[J]. Computers and Electrical Engineering, 2018, 69: 842-851. DOI:10.1016/j.compeleceng.2017.11.029