|
|
|
发布时间: 2022-02-28 |
清洁安全发电 |
|
|
|
收稿日期: 2020-12-24
基金项目: 上海市自然科学基金(19ZR1420400);新能源与储能运行控制国家重点实验室(中国电力科学研究院有限公司)开放基金(NYB51202001608)
中图法分类号: TB657
文献标识码: A
文章编号: 2096-8299(2022)01-0035-05
|
摘要
通过Fluent软件对CO2工质在喷射器中的流动进行模拟, 同时通过改变工作流体和引射流体的入口压力研究喷嘴临界截面直径对喷射系数的影响。模拟结果表明: 当保持喷射器的基本工作参数不变, 引射流体入口压力为一定值时, 喷射器喷射系数随喷嘴临界截面直径的减小而逐渐增大; 当保持喷射器的基本工作参数不变, 工作流体入口压力为一定值时, 喷射器喷射系数随喷嘴临界截面直径的增大而逐渐减小; 在喷射器的基本工作参数保持稳定时, 可以通过提高引射流体入口压力及工作流体入口压力2种方法提高喷射系数。
关键词
喷射器; 喷嘴直径; 数值模拟
Abstract
The flow of CO2 working fluid in ejector is simulated by Fluent software, and the influence of nozzle critical cross-section diameter on injection coefficient is studied by changing the inlet pressure of working fluid and ejector fluid.The simulation results show that when the basic working parameters of the ejector are kept unchanged and the inlet pressure of the ejector fluid is a certain value, the ejector injection coefficient increases gradually with the decrease of the critical cross-section diameter of the nozzle.When the basic working parameters of the injector are kept unchanged and the inlet pressure of the working fluid is a certain value, the injection coefficient of the injector decreases gradually with the increase of the critical cross-section diameter of the nozzle.While keeping the basic working parameters of the ejector stable, the injection coefficient can be improved by increasing the inlet pressure of the working fluid and injecting.
Key words
ejector; nozzle diameter; numerical simulation
朗肯循环[1]是一种高效的循环模式, 具有结构简单、适应性强等特点, 为使朗肯循环能够高效运行, 研究人员对工质进行了广泛的研究, 许多传统有机工质在运行时都会对环境造成极大伤害, 因此寻找一种环保安全的新型工质至关重要。CO2作为一种无机工质, 由于其具有优秀的热力学性质, 无毒无害不可燃, 所以是一种非常适合朗肯循环的高效工质。在超临界CO2热泵系统中[2], 喷射器是重要组成部件。朗肯循环效率与喷射器性能之间有紧密的联系, 而喷射器性能与工质的运行状态密不可分, 工质CO2的流动状态、相态等物理性质又受喷射器几何结构参数影响, 其中拉瓦尔喷嘴是将工作流体的压力能转化为速度能的核心部件, 其参数的变化将直接影响喷射器的整体工作性能, 因此有必要对喷射器的几何结构参数进行研究。
1 喷射器几何结构参数研究综述
NAKAGAWA M等人[3]通过实验对比研究了5 mm, 15 mm, 25 mm混合室长度的喷射器对有/无回热器的跨临界CO2制冷系统能效比(Coefficient of Performance, COP)的影响。研究结果表明: 混合室长度与喷射器效率之间有直接的联系, 混合室长度为15 mm时, 能使喷射器效率及系统COP达到最高, 提高约26%;而当混合室长度为5 mm且在无回热器的情况下, 最多可使COP下降10%。LIU F等人[4]探讨了喷嘴出口直径与混合室直径对喷射性能的影响。结果表明, 喷嘴出口直径与混合室直径的比值对喷射器的效率有重要的影响。何丽娟等人[5]通过搭建实验台, 以CO2, N2及R290为工质, 保持入口温度恒定, 通过改变引射压力和主流体压力, 研究了喷嘴截面直径对喷射器引射比的影响。结果表明: 在工作流体压力一定时, 喷射系数随着喷嘴截面直径的增大而减小; 在引射流体压力一定时, 喷射系数增大且随着喷嘴临界截面直径的增大而减小。夏在超等人[6]运用实验与模拟结合的方法, 对工质R236fa进行了喷射器性能研究。研究表明: 在喷射器处于给定工作参数条件时, 喷射器的喷嘴收敛段长度、喷嘴距、混合室长度参数均存在一个最佳值。此时喷射器的引射比、升压比将达到最大值; 而当扩散室的出口角度α增大时, 引射比、升压比将随之下降。
刘恒[7]对建立的CO2跨临界两相喷射器的三维计算流体力学(Computational Fluid Dynamics, CFD)模型进行了内部流动预测, 利用超临界CO2沸腾空化相变模型以及声速模型, 研究了喷射器几何结构混合段和扩散段尺寸对喷射器性能的影响。结果表明: 喷射器的扩散角最佳值为6°(设计工况值为8.2°); 在一定工况下存在最佳混合室长度和直径使喷射系数, 混合室长度的最佳值为27 mm(与设计工况值一致), 混合室直径的最佳值为2.5 mm(设计工况值为2.7 mm)。减小或增大混合室直径都会使喷射器接收室中的回流区域范围变大。
徐慧强等人[8]通过CFD模拟的方法对喷射器提高喷射系数的方法进行了研究。研究表明, 当喷嘴喉部及出口直径、喷嘴距、接收室收缩角、混合室长度及直径均处于一个最佳的区间时, 喷射器的最大流速、激波规模等物理状态会有一个较大的提升, 喷射系数达到最大值。
总之, 目前国内外大多数模拟超临界CO2相变均采取Zwart空化模型, 但对模型中蒸发冷凝系数鲜有关注。本文在传统Zwart空化模型的基础上改进系数, 进一步完善超临界CO2相变过程, 分析喷射器内部流动的速度和压力场, 同时, 对在不同引射流体和工作流体压力下, 喷嘴临界截面直径对喷射器喷射系数的影响进行了分析。
2 模型的建立
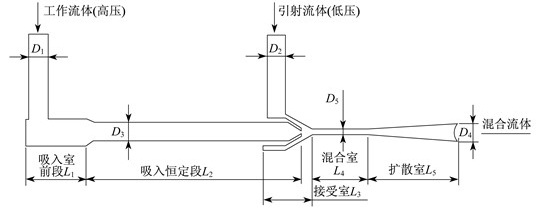
两相流喷射器结构如图 1所示。喷射器设计方案是根据文献[7]中两相流喷射器的设计方法确定的。其中: D1为主进口直径, D2为次进口直径, D3为吸入室恒定段直径, D4为扩散室出口直径, D5为混合室直径; L1为吸入室前段长度, L2为吸入式室恒定段长度, L3为接受室长度, L4为混合室长度, L5为扩散室长度。
连续性方程为
| $ \frac{{\partial {\mathit{\rho }_{\rm{m}}}}}{{\partial t}} + \nabla \left( {{\mathit{\rho }_{\rm{m}}}{\mathit{\boldsymbol{u}}_{\rm{m}}}} \right) = {{\dot S}_{\rm{m}}} $ | (1) |
式中: ρm——喷射器中所有流体混合密度, kg/m3;
▽——哈密顿算子;
um——混合流体速度矢量, m/s;
动量守恒方程为
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left( {{\mathit{\rho }_{\rm{m}}}{\mathit{\boldsymbol{u}}_{\rm{m}}}} \right) + \nabla \left( {{\mathit{\rho }_{\rm{m}}}{\mathit{\boldsymbol{u}}_{\rm{m}}}{\mathit{\boldsymbol{u}}_{\rm{m}}}} \right) = \\ - \nabla \mathit{p} + \nabla \left[ {{\mathit{\boldsymbol{\mu }}_{\rm{m}}}\left( {\nabla {\mathit{\boldsymbol{u}}_{\rm{m}}} + \nabla \mathit{\boldsymbol{u}}_{\rm{m}}^{\rm{T}}} \right)} \right] + \\ {\mathit{\rho }_{\rm{m}}}g + F + \nabla \left( {\sum\limits_{k = 1}^n {{\alpha _k}} {\mathit{\rho }_k}{v_{{\rm{dr}}, k}}} \right) \end{array} $ | (2) |
式中: ▽ρ——压力梯度, Pa/m;
μm——混合流体的黏度系数, Pa/s;
▽umT——混合流体速度矢量求偏导后的转置;
g——重力加速度, m/s2;
F——外部体积力, N/m3;
αk——相k的体积分数;
ρk——相k的密度, kg/m3;
vdr, k——第k相的偏移速度, m/s。
能量守恒方程为
| $ \begin{array}{c} \frac{\partial }{{\partial t}}\sum\limits_{k = 1}^n {\left( {{\mathit{\alpha }_k}{\mathit{\rho }_k}{E_k}} \right)} + \nabla \sum\limits_{k = 1}^n {\left[ {{\mathit{\alpha }_k}{\mathit{\boldsymbol{u}}_k}\left( {{\mathit{\rho }_k}{E_k} + p} \right)} \right]} = \\ \nabla {l_{{\rm{eff}}}}\nabla T + {S_{\rm{E}}} \end{array} $ | (3) |
式中: Ek——机械能, J/kg;
uk——相k的速度矢量, m/s;
p——运动压力, Pa;
leff——有效热传导系数, W/(m·K);
T——温度, K;
SE——流体的内热源, J。
超临界CO2空化相变采用文献[7]中的控制方程, 之后根据本文喷射器模型进行修改, 对蒸发系数及冷凝系数进行模拟试验。其中, 空化相变模型可简化为
| $ {m_{\rm{e}}} = {F_{\rm{e}}}\frac{{3{\mathit{\alpha }_{{\rm{nuc}}}}(1 - \mathit{\alpha }){\mathit{\rho }_{\rm{g}}}}}{{{R_{\rm{B}}}}}\sqrt {\frac{2}{3} \cdot \frac{{{p_{\rm{g}}} - p}}{{{\mathit{\rho }_1}}}} $ | (4) |
| $ {m_{{\rm{cond}}}} = {F_{{\rm{cond}}}}\frac{{3\mathit{\alpha }{\mathit{\rho }_{\rm{g}}}}}{{{R_{\rm{B}}}}}\sqrt {\frac{2}{3} \cdot \frac{{p - {p_{\rm{g}}}}}{{{\mathit{\rho }_1}}}} $ | (5) |
式中: me——蒸发速率;
Fe——蒸发系数;
αnuc——成核位置体积分数;
α——气相体积分数;
ρg——气相密度;
pg——气相压力;
ρ1——液相密度;
mcond——冷凝速率;
Fcond——冷凝系数;
RB——气泡半径。
为使模型达到较好的收敛效果, 取Fe=0.5, Fcond=0.000 1, RB=1×10-6m, αnuc=5×10-4。
3 模型验证
3.1 数值方法及边界条件
本文采用Fluent软件模拟喷射器内部流动, 模拟基于压力求解器, 使用Mixture混合物模型, 主进口流体设为超临界态CO2, 次进口流体设为气态CO2, 使用非均相模型完成两相间滑移速度。喷射器内部流动情况剧烈。为精确描述喷射器内的两相流动及相变, 选取Realizable的k-ε湍流模型。该模型对复杂几何的内外部流动问题特别适用。同时对喷射器的近壁面采取标准壁面函数, 避免因喷射器内雷诺数太高而引起的计算误差问题。模拟计算耦合方式设为coupled, 壁面设置为两相之间无滑移条件, 温度设置为绝热条件, 具体边界条件及模拟方法如表 1所示。
表 1
喷射器的边界条件及模拟方法
| 位置 | 压力/MPa | 温度/K | 流体工质 | 气相体积分数 | 热力学状态 | 密度/(kg·m-3) | 比热/[J·(kg·K)-1] |
| 工作流体入口 | 8.0~10.0 | 313 | CO2 | αv=0 | 超临界态 | 202.930 | 1 652.4 |
| 引射流体入口 | 4.2~4.6 | 289 | αv=1 | 气态 | 53.407 | 1 085.8 | |
| 混合流体出口 | 5.0 | 气液两相 |
3.2 模型和网格验证
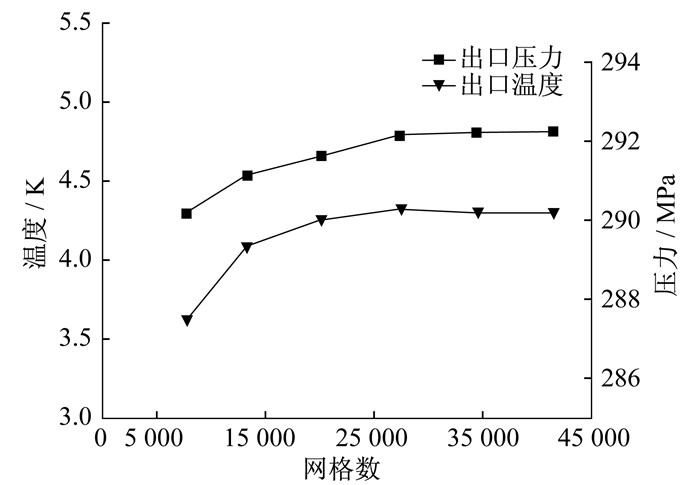
由于喷射器内流动复杂, 故对模型全局使用计算能力更高的结构化网格, 同时对壁面边界层采用加密方式提高计算精确度, 总体网格质量参数Skewness在0.9附近[9]。在网格无关性验证中, 划分6种数量不同的网格, 以此来准确描述喷射器内部复杂的几何结构。图 2展示了在9.5 MPa下不同网格尺度下的模拟结果, 网格数量分别为7 739, 13 256, 20 102, 27 360, 34 360, 41 360。从曲线的趋势可以看出, 随着网格数的增多, 喷射器出口温度与压力逐渐趋于稳定。因此, 本文采用网格数为27 360来进行模拟。
表 2为不同工况下模拟结果与实验结果对比[10]。其中, pd表示工作流体入口压力, pc表示引射流体入口压力, d表示喷嘴临界截面直径, μexp表示喷射系数实验值, μcfd表示喷射系数模拟值。通过喷射系数数据对比检验模拟的正确性。由模拟结果可知, 在相同的入口压力和喷嘴临界截面直径、不同的引射压力下, 喷射系数最大误差δ为8.5%, 模拟误差在工程实践中均为合理范围, 因此认定模拟准确、合理。
表 2
不同工况下模拟结果与实验结果对比
| 工况 | pd /MPa | pc /MPa | d/mm | μexp | μcfd | δ/% |
| 1 | 9.5 | 4.6 | 1.5 | 0.35 | 0.38 | 8.5 |
| 2 | 10.0 | 4.1 | 1.5 | 0.47 | 0.44 | 6.3 |
| 3 | 11.3 | 3.4 | 1.5 | 0.56 | 0.51 | 7.1 |
4 模拟结果分析与讨论
4.1 喷射器流动分析
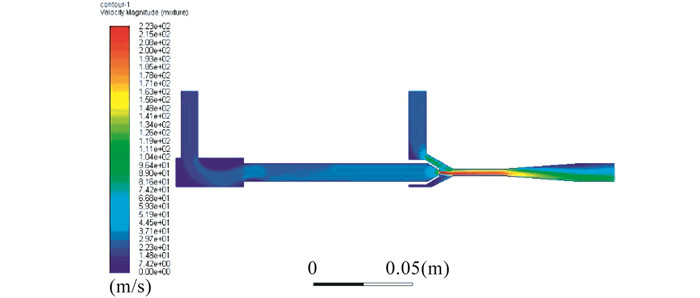
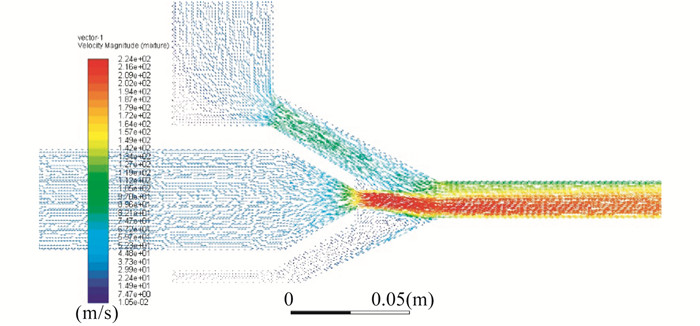
图 3和图 4分别为喷射器内制冷剂的流体速度分布云图和速度矢量分布图。此时工况为主进口9.5 MPa, 313 K, 次进口为4.6 MPa, 289 K, 喷射器背压为5 MPa, 喉口直径为1.5 mm。
从图 3和图 4可以看出: 速度较低(15.8 m/s)的主流体进入后, 主流体速度不断增加, 逐渐增加到吸入室水平段的28 m/s, 在喉口前达到90 m/s, 而在喉口出口, 速度达到最大值223 m/s; 同时, 引射流体被低压高速的主流体引射, 以25 m/s的初速度进入, 之后二者进行初步混合; 在混合室渐缩段, 引射流体速度迅速上升, 在混合室恒定段内继续进行混合, 水平中心速度约为210 m/s, 最后在扩散室中速度减小, 喷嘴出口的速度约为60 m/s。
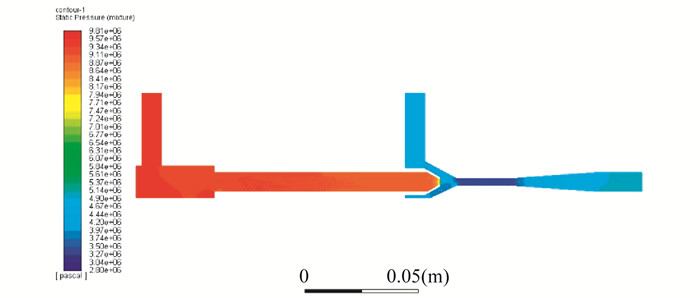
图 5为喷射器内压力分布云图。从图 5可以看出: 高压(9.5 MPa)主流体进入后, 在吸入室中变化不大, 在喉口出口由于喷嘴结构特点, 压力降至4 MPa, 超临界CO2发生相变; 同时卷吸低压(4.60 MPa)的被引射流体开始进行混合, 在混合室和扩散室中, 压力出现先减小后增大的阶跃性变化, 最后扩散室出口压力为5 MPa。
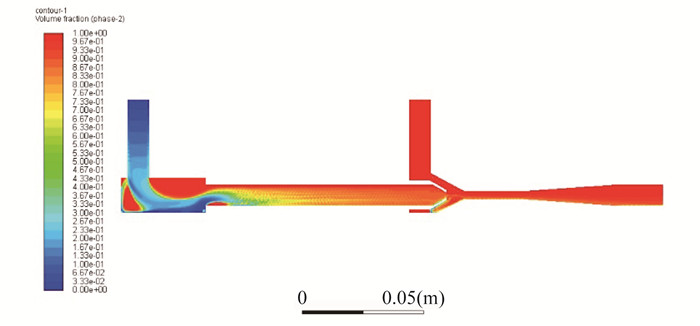
喷射器内部的气相体积分数分布云图如图 6所示。从图 6可以看出: 主进口全部为液相, 进入后不久即发生相变, 相变速率随着液相不断前进不断增大, 气相也逐渐增多, 在吸入室中气相体积分数从0增加至喉口前0.8左右, 说明在喉口前相变已经发生; 主流体通过喉口后, 气相体积分数继续增加至0.9左右, 经混合室和扩散室后, 最终在扩散出口气相体积分数为0.95。
4.2 不同引射流体入口压力下喷嘴临界截面直径对喷射器性能的影响
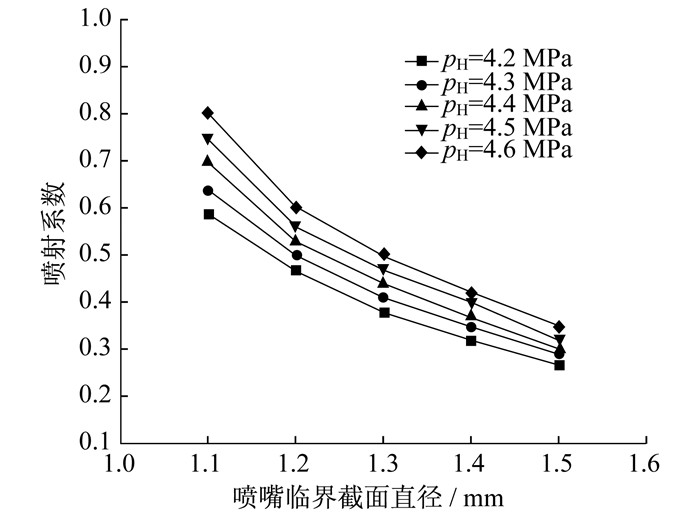
当喷射器工作流体的参数保持一定(工作流体入口温度为40 ℃, 工作流体入口压力为9.5 MPa, 喷射器背压为5 MPa)时, 改变引射流体的入口压力PH由4.2 MPa至4.6 MPa变化和喷嘴的临界截面直径由1.1 mm至1.5 mm变化, 则此时喷射器性能变化规律如图 7所示。
由图 7可知, 在模拟范围内, 当工作流体入口压力一定时, 喷射系数随着临界截面直径的增大而不断减小。其主要原因是, 随着喷嘴临界截面直径增大, 工作流体的质量流量增大, 工作流体所需流通面积随之增大, 从而减小了引射流体的有效流通面积, 引射流体质量流量随之较小, 致使喷射系数随之减小。
同时, 喷射系数随引射流体入口压力的提升而增大。其主要原因是工作流体入口压力一定时, 喷嘴的出口压力固定, 此时若引射流体压力增大, 则二者的压差增大, 对引射流体的吸引力增强, 吸入量也增大, 入口流量变化不大, 导致引射比增大。
4.3 不同工作流体入口压力下喷嘴临界截面直径对喷射器性能的影响
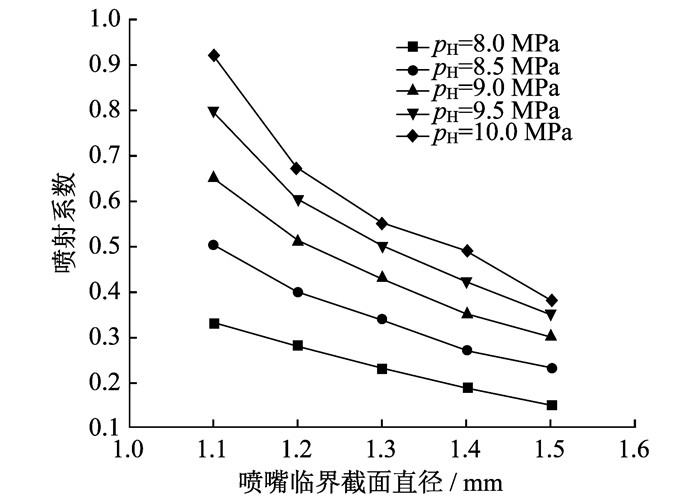
当喷射器工作流体的参数保持一定(工作流体入口温度为40 ℃, 引射流体入口压力为4.6 MPa, 喷射器背压为5 MPa)时, 改变工作流体的入口压力由8 MPa至10 MPa变化, 喷嘴的临界截面直径由1.1 mm至1.5 mm变化, 则此时喷射器性能变化规律如图 8所示。
由图 8可知, 当工作流体入口压力为一定值时, 喷射器喷射系数随喷嘴临界截面直径的增大而逐渐减小。这是因为当喷嘴临界截面直径减小时, 喷嘴出口处流速增大, 同时吸入室内压力降低, 工作流体卷吸引射流体能力升高, 导致引射流体流量增加, 由引射比公式可知, 引射比也随之增大。另外, 当工作流体的入口压力增大时, 喷射器的引射比也随之增大。主要原因为, 当工作流体压力增大时, 流体所具有的能量增大, 在喷嘴出口处具有更高的速度, 压力降低更大, 引射流体吸入量相应增加, 引射比随之增大。
5 结论
(1) 液相在进入喷射器后, 速度逐渐增大, 至喉口处速度发生突变, 出口处达到最大值223 m/s。
(2) 进入扩散室后, 压力增大, 速度降低, 在出口处降低至60 m/s; 当工作流体温度为40 ℃、喷射器背压为5 MPa、工作流体入口压力为10 MPa、引射流体入口压力在4.2~4.6 MPa变化时, 喷射器喷射系数随喷嘴临界截面直径的减小而逐渐增大。
(3) 当工作流体温度为40 ℃、喷射器背压为5 MPa、引射流体入口压力为2.6 MPa、工作流体入口压力在8.0~10.0 MPa变化时, 喷射器喷射系数随喷嘴临界截面直径的减小而逐渐增大。
(4) 在保持喷射器的基本工作参数稳定时, 喷射系数的提高可以采取提高引射流体入口压力及工作流体入口压力2种方法。
参考文献
-
[1]张鑫, 赵贤聪, 苍大强, 等. 超临界朗肯循环热力性能研究[J]. 热能动力工程, 2015, 30(2): 228-232.
-
[2]丁涛, 梁立军, 李震. 以二氧化碳为工质的朗肯循环特性分析[J]. 工程热物理学报, 2015, 36(2): 410-413.
-
[3]NAKAGAWA M, MARASIGAN A R, MATSUKAWA T, et al. Experimental investigation on the effect of mixing length on the performance of two-phase ejector for CO2 refrigeration cycle with and without heat exchanger[J]. International Journal of Refrigeration, 2010, 34(7): 1604-1613.
-
[4]LIU F, LI Y, ECKHARD A G. Performance enhancement of CO2 air conditioner with a controllable ejector[J]. International Journal of Refrigeration, 2012, 35(6): 1604-1616. DOI:10.1016/j.ijrefrig.2012.05.005
-
[5]何丽娟, 王飒, 王淑旭, 等. 几何结构参数对喷射器性能影响实验研究[J]. 低温工程, 2019(6): 6-11. DOI:10.3969/j.issn.1000-6516.2019.06.002
-
[6]夏在超, 李建新, 高德, 等. 几何结构对喷射器性能影响的CFD分析及实验研究[J]. 制冷学报, 2014, 35(3): 45-49. DOI:10.3969/j.issn.0253-4339.2014.03.045
-
[7]刘恒. 基于沸腾空化的跨临界CO2两相喷射器的数值模拟及优化[D]. 南宁: 广西大学, 2018.
-
[8]徐慧强, 王景富, 张东洋, 等. 结构参数对热压机喷射特性影响效果探究[J]. 应用科技, 2020, 47(4): 95-99.
-
[9]汤本凯. 压缩-喷射制冷系统及喷射器的研究[D]. 郑州: 郑州大学, 2013.
-
[10]邓嘉欣, 刘方, 朱威全. 跨临界CO2喷射式热泵热电池控制优化[J]. 低温与超导, 2019, 47(6): 84-90.