|
|
|
发布时间: 2022-02-28 |
计算机与信息科学 |
|
|
|
收稿日期: 2021-08-20
基金项目: 国家重点研发计划(2020YFB1711001)
中图法分类号: TP301.6;TP23
文献标识码: A
文章编号: 2096-8299(2022)01-0089-05
|
摘要
自动化分拣仓储包含大量的分拣任务, 需要多个自动导引车(AGV)来辅助人工完成快速分拣任务。为了提高效率, 在保障AGV电量的前提下, 以AGV完成任务的空载时间与AGV的空置率为优化目标, 对多AGV的碰撞进行了冲突分析, 并通过改进的Q-learning算法来生成AGV的无冲突搬运路径; 为了完成多AGV路径和调度综合优化, 提出了一种改进遗传算法, 算法采用精英保留和轮盘赌的方式选择个体, 运用自适应的交叉和变异算子来进行进化操作。最后, 通过仿真验证了算法的有效性。
关键词
多AGV; 路径规划与任务调度; Q-learning算法; 改进遗传算法
Abstract
Automated sorting warehousing involves a large number of sorting tasks and requires multiple automated guided vehicles (AGVs) to assist manually in completing quick sorting tasks.In order to improve efficiency, under the premise of guaranteeing AGV power, the empty load time of AGV task and AGV's vacancy rate are optimized, the collision of multi-AGV is analyzed, and the conflict-free handling path of AGV is generated by the improved Q-learning algorithm.Finally, the validity of the algorithm is verified by simulation.
Key words
multi-automated guided vehicle; path planning and task scheduling; Q-learning algorithm; improved genetic algorithm
随着电子商务与工业自动化等行业的飞速发展, 仓储物流行业在各个领域扮演的角色也越来越重要, 人们迫切需要构建一个更加高效的自动化仓储系统。其中, 自动导引车(Automated Guided Vehicle, AGV)是实现整个自动化仓储系统的关键因素之一。订单拣选作为仓库集成系统的关键环节之一, 是影响物流配送中心作业效率的重要因素, AGV的出现实现了仓储系统从“人到货”到“货到人”的转变, 拣选效率提高了2~4倍[1-2]。
目前, 关于AGV任务调度与路径规划问题的研究都聚焦于单一问题[3], 然而两者存在相同的优化目标, 综合优化能更好地提高AGV分拣效率。
对于AGV任务调度问题, 文献[4]建立了一个混合整数规划模型, 采用文化算法和改进遗传算法的混合算法进行优化调度; 文献[5]将AGV无冲突路径的任务调度问题描述为整数规划问题进行求解; 文献[6]通过改进的Memetic算法来对多AGV调度问题进行求解, 但并未考虑AGV之间的碰撞冲突以及死锁。
AGV路径规划的好坏直接影响系统的效率[7]。路径规划问题的常用算法包括传统的Dijkstra算法[8]与A*算法[9], 近年来Q-learning算法[10]、遗传算法[11], 以及PSO算法[12]也陆续出现在求解路径规划问题上, 但是大多仅能求解单AGV的路径问题。对于多AGV系统, 如何避免AGV的路径冲突尤为重要。文献[13]提出了一种在线学习的Q-learning算法, 通过构建奖惩矩阵的形式, 实现了多AGV的无冲突路径规划; 文献[14]通过预约表、改进A*算法与动态加权地图, 实现了多AGV的路径协同优化。
上述文献在研究AGV任务调度问题时, 大多将AGV运行路径进行固定且很少考虑AGV间的碰撞冲突, 同时, 研究AGV路径优化问题时, 大多默认分配给AGV的任务调度是固定的。另外, 当前研究大都忽略了AGV电量的影响。因此, 本文针对自动化拣选仓储的多AGV环境, 在考虑AGV电量的情况下, 综合研究任务调度和路径优化问题。首先, 针对路径规划问题, 设计了多AGV的路径规划算法, 同时考虑AGV电量的影响, 综合优化多AGV任务调度和路径规划, 最终通过本文设定的AGV冲突优先级, 生成多AGV的无冲突路径。
1 任务调度与路径规划问题描述
通过栅格化建模方式建立的自动化仓储模型如图 1所示。
图 1中, 仓储的货架排列是整齐对称的, 多AGV在仓储环境中工作。其中, ①为拣选区, 人工拣选区域; ②为空载AGV, 前往目标点搬运货架; ③为载货AGV, 搬运货架中; ④为货架, AGV的搬运目标; ⑤为充电区, AGV电量不足时会驶入充电。
为了便于求解, 本文对多AGV的运行场景简化如下
(1) AGV的每条通行道是单向的, 且相邻通行道的通行方向相反;
(2) 每个货架仅搬运1次;
(3) 忽略货架重量的影响, AGV装货与卸货时间固定为2 s;
(4) AGV运行速度是固定的, AGV运动一个栅格的时间为1 s;
(5) AGV执行一次启停操作时间为2 s, AGV执行一次转弯操作时间为3 s;
(6) AGV在载货状态的电量是空载状态的2倍, 空载AGV运行1 s消耗电量1;
(7) AGV不可沿对角线跨越栅格。
AGV在执行任务过程中, 根据其运行状态的不同, 将其分为载货和空载2个工作状态。载货状态指AGV将目标货架搬运到拣选区再返回时的状态, 此时AGV只能在规定巷道内行驶, AGV的运动障碍点为固定货架与其他AGV; 空载状态, 即AGV前往目标货架点时的状态, AGV可从规定巷道内行驶, 亦可从货架下方行驶, 此时AGV在仓储环境中运动时, 障碍仅为其他AGV。
为方便描述, 本文定义以下符号: i表示AGV编号; j表示任务编号; n表示机器人数量; m表示任务数量; AGVi表示编号为i的AGV; Yi表示AGVi的任务搬运序列; Yi(r) 表示Yi的第r个任务; D表示AGV设定的最低电量; Ei表示AGVi的电量; hij表示AGVi执行第j个任务载货运行时间; kij表示AGVi执行第j个任务空载运行时间; Ti表示AGVi的搬运任务完成时间; Tes表示为电量充足的AGV搬运任务完成时间最大值与最小值的差值; S1i表示AGVi空载状态下的停车等待次数; S2i表示AGVi载货状态下的停车等待次数; Ts表示AGV单次停车避让时间。
Ti的计算公式为
| $ T_{i}=\sum\limits_{r=1}^{Y_{i}} h_{i r}+k_{i r}+T_{\mathrm{s}}\left(S_{1 i}+S_{2 i}\right) $ | (1) |
AGV完成任务的空载时间与AGV空置率的优化目标函数为
| $ \text { fitness }=\min \left(\sum\limits_{i=1}^{n} \sum\limits_{r=1}^{Y_{i}} k_{i r}+T_{\mathrm{es}}\right) $ | (2) |
考虑AGV电量的影响, 设置AGV完成任务后的电量不能低于设定值D, 即
| $ \begin{gathered} E_{i}-\sum\limits_{r=1}^{Y_{i}}\left[h_{i r} \times 2+k_{i r}+\right. \\ \left.T_{\mathrm{s}}\left(S_{1 i}+2 \times S_{2 i}\right)\right] \geqslant D \end{gathered} $ | (3) |
在调度过程中, 若AGV电量低于设定值时, 应对AGV所承担任务进行舍弃, 使之电量不能低于设定值, 且将此AGV设定为低电量状态。
2 多AGV路径规划算法
若搬运路径确认的情况下, 多AGV搬运问题可以理解为多旅行商问题, 针对多AGV调度问题本文设计了一种改进的遗传算法。
在执行任务序列Yi时, 采用一种基于Q-learning的路径规划算法。Q-learning算法通过建立奖励函数R和Q值表, 分别用来存储瞬时奖励和Q值函数值。通过AGV的当前位置s和相应的路径动作a, 计算并更新对应的Q值函数值, 记为Q(s, a)。最终通过选择最大的累计回报值, 选择AGV的下一位置s′, 从而生成AGV的运动路径。
将奖励函数R分为主奖励函数R1与辅助奖励函数R2, 即
| $ R=R_{1}+R_{2} $ | (4) |
首先, 建立主奖励函数R1为
| $ R_{1}= \begin{cases}100, \quad\text { 到达目标点 } \\ -100, \quad\text { 发生碰撞 } \\ -5, \quad \text { 转弯操作 } \\ 0, \quad\text { 其他动作 }\end{cases} $ | (5) |
对于传统的Q-learning算法, 存在收敛速度慢等问题, 因此本文引入了导向机制, 用以建立辅助奖励函数R2。
| $ R_{2}=C_{(s, \text { goal })}-C_{\left(s^{\prime}, \text { goal }\right)} $ | (6) |
式中: C(s, goal)——AGV当前位置点到目标点的欧式距离;
C(s′, goal)——AGV下一位置点到目标点的欧式距离。
当R2为正值时, 表示AGV正在向目标点靠近, 应给予奖励; 反之, 应给予惩罚。引入导向机制, 可以加快Q-learning算法的迭代速度, 使得AGV更快地向目标点靠近。
本文对Q值函数值进行初始化操作, 同时在Q值函数值中加入导向机制, 减少算法前期大量的无用迭代, 以提高算法效率。具体公式为
| $ Q_{(s, a)}=C_{(s, \text { goal })}-C_{\left(s^{\prime}, \text { goal }\right)} $ | (7) |
| $ \begin{aligned} Q_{(s, a)}^{\prime}=&(1-\alpha) Q_{(s, a)}+\alpha\left(R_{(s, a)}+\right.\\ &\left.\beta \max Q_{\left(s^{\prime}, a^{\prime}\right)}\right) \end{aligned} $ | (8) |
式中: Q′(s, a)——更新后的Q值函数值;
α——学习率, α∈[0, 1], 定义了Q值更新占原Q值的比例;
R(s, a)——当前状态下, 系统采取的路径动作获得的奖励;
β——折扣因子, β∈[0, 1], 定义未来奖励的重要程度;
a′——下一状态所采取的路径动作;
Q(s′, a′)——下一状态下所能得到的最大Q值函数值。
AGV在运行过程中, 如果同一时间内有2台或以上AGV占据了同一栅格, 即发生了AGV冲突。为了解决AGV的冲突问题, 本文设置AGV冲突避让规则如下。
规则1 低电量机器人获得最高优先级, 即: AGV设置2个电量等级, 机器人电量不可低于20%的电量, 否则, 将前往充电区; 对低电量机器人赋予高优先级。
规则2 若不满足规则1, 即AGV的电量充足, 则先判断AGV是否为载货状态, 载货状态的AGV赋予高优先级。
规则3 若不满足规则1和规则2, 即AGV电量充足且在相同工作状态下发生冲突, 则计算各个AGV完成分配的任务序列总时间长短, 赋予搬运时间长的机器人高优先级。
规则4 若AGV均不满足以上3条规则, 则随机确定AGV的冲突优先级。
规则1的制定是为了保证AGV的电量充足, 避免AGV因为电量不足, 从而导致碰撞或死锁; 规则2的制定, 是为了减少AGV的电量消耗; 规则3的制定, 使得AGV的最大搬运时间不会再增加, 降低AGV空置率。根据以上规则, 在AGV发生冲突时, 使得高优先级AGV直接通过, 低优先级AGV停车避让。
3 改进遗传算法求解调度问题
本文针对AGV搬运任务序列提出了一种改进的遗传算法, 设计了双重染色体编码方案, 使得每个个体中都包含各AGV的搬运任务序列; 然后通过本文设置的自适应交叉和变异因子对个体进行进化。AGV的搬运任务序列表示为Y={r1, r2, r3, …, rm}。为了提高AGV的运行效率, 需要通过调度来生成一条有序地任务序列, 使AGV按照序列有序地执行订单任务, 以保障: 低电量机器人不会承担超过设定值电量的任务; AGV执行任务的路径最短; 降低AGV最大任务完成时间, 从而降低AGV空置率。
3.1 种群初始化
本文为解决多AGV的任务调度问题, 设计了一种双重染色体编码方案。染色体分为2层: 第1层决定任务序列; 第2层决定AGV编码。例如, 任务数m为4, AGV数量n为2。染色体Ca为
| $ C_{\mathrm{a}}=\left[\begin{array}{llll} 4 & 2 & 3 & 1 \\ 1 & 2 & 2 & 1 \end{array}\right] $ | (9) |
此时AGV的搬运序列为: Y1为4-1;Y2为2-3。
3.2 选择
遗传算法通过选择最优的个体作为父代, 然后通过进化操作产生新的子代, 但如果将所有的个体都放入进化过程, 个体中的优质基因很容易被破坏, 因此本文通过轮盘赌和精英保留的方式进行个体选择。将种群中适应度值前10%的个体进行保留, 确保种群的群优良, 然后再通过轮盘赌的方式选择个体成为父代。
3.3 交叉变异
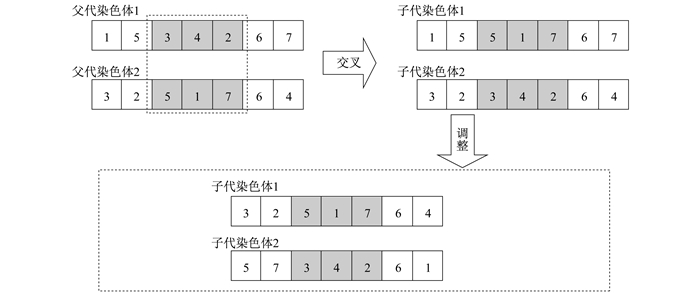
遗传算法的交叉过程为随机产生两个数(大小不能超过染色体的长度), 通过两个随机数可选中父代染色体的两段基因片段, 然后将两个基因片段进行互换, 即可生成两个子代染色体, 染色体进行基因片段互换后, 可能会使得个体中出现重复任务, 需要对染色体进行调整, 最终生成交叉后的子代染色体。具体交叉操作如图 2所示。
染色体交叉过程中, AGV编码可与任务序列编码一起变动。在算法进化过程中, 如果给予所有个体相同的交叉概率Cr, 在进化过程中会造成种群优良基因的流失, 因此本文提出一种自适应交叉因子。对每1对交叉的个体赋予1个交叉概率, 当该个体的质量较好时, 赋予较低的交叉概率, 希望将个体保留下来; 反之, 则提高交叉概率, 希望生成更好的个体。
| $ C_{\mathrm{r}}=\left\{\begin{array}{l} C_{\mathrm{rmax}}-\left(C_{\mathrm{rmax}}-C_{\mathrm{rmin}}\right) \times\left(\frac{f^{\prime}-f_{\mathrm{avg}}}{f_{\max }-f_{\mathrm{avg}}}\right), \\ \ \ \ \ \ \ \ \ f^{\prime} \leqslant f_{\mathrm{arg}} \\ C_{\mathrm{rmax}}, f^{\prime}>f_{\mathrm{avg}} \end{array}\right. $ | (10) |
式中: Crmax, Crmin——最大和最小交叉概率;
f′——当前2个个体中最高的适应度值;
favg, fmax——种群中个体平均和最高适应度值。
在算法迭代前期, 种群个体的适应差值较大, 需要较大的交叉概率来生成新的个体, 而随着迭代逐渐靠近中后期, 此时的种群个体的适应差值逐渐减小, 需要减小交叉概率, 因此设计了随算法迭代次数而变化的最大交叉概率为
| $ C_{\mathrm{rmax}}=\left\{\begin{array}{l} 0.8,0<g_{\mathrm{en}} \leqslant \frac{1}{4} G_{\mathrm{en}} \\ 0.7, \frac{1}{4} G_{\mathrm{en}}<g_{\mathrm{en}} \leqslant \frac{1}{2} G_{\mathrm{en}} \\ 0.6, \frac{1}{2} G_{\mathrm{en}}<g_{\mathrm{en}} \leqslant G_{\mathrm{en}} \end{array}\right. $ | (11) |
式中: gen, Gen——当前和最大迭代次数。
变异操作时, 采用单点变异的方式, 即产生两个随机数, 确定父代个体中2个基因点, 将选中的2个基因点位置进行互换, 即可得到变异后子代个体。AGV染色体编码与任务序列编码一起变动用来避免算法早熟且可以改善算法的局部搜索能力。本文设计的自适应变异算子Mr计算公式如下
| $ M_{\mathrm{r}}=\left\{\begin{array}{l} M_{\mathrm{rmax} }-\left(M_{\mathrm{rmax}}-M_{\mathrm{rmin}}\right) \times \\ \ \ \ \ \ \ \ \ \left(\frac{f^{\prime}-f_{\mathrm{avg}}}{f_{\mathrm{max}}-f_{\mathrm{avg}}}\right), f^{\prime} \leqslant f_{\mathrm{avg}} \\ M_{\mathrm{r} \max }, f^{\prime}>f_{\mathrm{avg}} \end{array}\right. $ | (12) |
| $ M_{\mathrm{rmax}}=\left\{\begin{array}{l} 0.2,0<g_{\mathrm{en}} \leqslant \frac{1}{4} G_{\mathrm{en}} \\ 0.3, \frac{1}{4} G_{\mathrm{en}}<g_{\mathrm{en}} \leqslant \frac{1}{2} G_{\mathrm{en}} \\ 0.4, \frac{1}{2} G_{\mathrm{en}}<g_{\mathrm{en}} \leqslant G_{\mathrm{en}} \end{array}\right. $ | (13) |
式中: Mrmax, Mrmin——最大和最小变异概率。
4 仿真验证
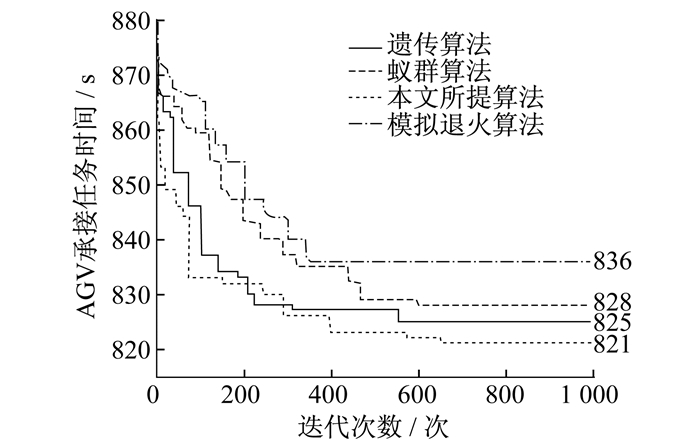
构建仿真场景模型, 设置基本参数如下: AGV数量为5, 任务数量为100, 2#AGV初始电量为低电量4 000, 其他编号的AGV初始电量为满电量10 000, AGV最低运行电量D为2 000。算法参数设置如下: α为0.6, β为0.2;初始种群数量为100, 最大迭代次数为2 000, 最小交叉概率为0.3, 最小变异概率为0.1。为了更加直观地观察算法的性能, 将本文所提算法与其他算法进行对比, 结果如图 3所示。
由图 3可知: 本文所提算法在650代取得了最小值821, 而遗传算法、蚁群算法和模拟退火算法分别在555, 596, 343取得最小值825, 828, 836;本文所提算法在396代收敛到823, 就已经超越其他算法的最优收敛值。因此, 本文所提算法在收敛速度上要优于其他算法。
在最终求解的路径结果上, 表 1和表 2分别给出了4种算法的AGV运行时间以及AGV空置时间。
表 1
AGV运行时间对比
| AGV编号 | AGV运行时间 | |||
| 遗传算法 | 蚁群算法 | 模拟退火算法 | 本文所提算法 | |
| 1# | 1 689 | 1 700 | 1 670 | 1 663 |
| 2# | 1 261 | 1 261 | 1 261 | 1 261 |
| 3# | 1 658 | 1 618 | 1 618 | 1 668 |
| 4# | 1 702 | 1 689 | 1 752 | 1 652 |
| 5# | 1 690 | 1 650 | 1 650 | 1 680 |
表 2
AGV空置时间对比
| 算法 | 空置时间 |
| 遗传算法 | 44 |
| 蚁群算法 | 82 |
| 模拟退火算法 | 134 |
| 本文所提算法 | 28 |
由表 1和表 2可以看出: 对低电量2#AGV的调度和路径优化, 所有算法都得出了相同的规划结果; 而对于其他编号的AGV, 本文所提算法的AGV运行时间和AGV空置时间更短, 系统的运行效率更高。由此可以得出本文所提算法在求解质量上优于其他算法。
5 结语
本文针对多AGV的路径及调度优化问题, 综合AGV完成任务的空载时间与AGV的空置时间为目标展开研究。针对路径优化过程, 通过加入导向机制用来改善Q-learning算法的效率低下问题。针对多AGV路径和调度的综合优化, 本文通过设计自适应的交叉和变异因子来改善遗传算法的效率以及局部最优问题。最后通过仿真验证, 本文算法在收敛速度和求解质量方面要优于其他算法, 在一定程度上体现了该算法的高效性。
参考文献
-
[1]邹爽心. 仓储机器人的应用现状与发展战略探讨[J]. 物流工程与管理, 2013, 35(6): 171-172.
-
[2]吴颖颖, 孟祥旭, 王艳艳, 等. "货到人"拣选系统订单排序优化[J]. 机械工程学报, 2016, 52(4): 206-212.
-
[3]余娜娜, 李铁克, 王柏琳, 等. 自动化分拣仓库中多AGV调度与路径规划算法[J]. 计算机集成制造系统, 2020, 26(1): 171-180.
-
[4]曾亮, 詹逸鹏, 王粟. 基于文化混合算法的多AGV调度研究[J]. 现代电子技术, 2021, 44(9): 105-109.
-
[5]MIYAMOTO T, INOUE K. Local and random searches for dispatch and conflict free routing problem of capacitated AGV systems[J]. Computers & Industrial Engineering, 2016, 91: 1-9.
-
[6]徐立云, 陈延豪, 高翔宇, 等. 混流柔性加工单元自动导引小车的调度优化[J]. 同济大学学报(自然科学版), 2017, 45(12): 1839-1846.
-
[7]贺丽娜, 楼佩煌, 钱晓明, 等. 基于时间窗的自动导引车无碰撞路径规划[J]. 计算机集成制造系统, 2010, 16(12): 2630-2634.
-
[8]王海霞. 一种仓储AGV路径规划最优策略方法的实现[J]. 计算机与网络, 2021, 47(9): 63-66.
-
[9]王云峰, 曹小华, 郭兴.基于改进A*算法和系统短期状态预测的仓储AGV路径规划方法[J/OL].计算机集成制造系统: 1-22[2021-08-17].
http://kns.cnki.net/kcms/detail/11.5946.TP.20210809.1137.008.html . -
[10]王鼎新. 基于改进Q-learning算法的AGV路径规划[J]. 电子设计工程, 2021, 29(4): 7-10.
-
[11]徐梦颖, 王娇娇, 刘宝, 等. 基于改进遗传算法的AGV路径规划[J]. 石河子大学学报(自然科学版), 2021, 39(3): 391-396.
-
[12]康玉祥, 姜春英, 秦运海, 等. 基于改进PSO算法的AGV路径规划及实验[J]. AGV, 2020, 42(1): 71-78.
-
[13]王毅然, 经小川, 田涛, 等. 基于强化学习的多Agent路径规划方法研究[J]. 计算机应用与软件, 2019, 36(8): 165-171.
-
[14]张丹露, 孙小勇, 傅顺, 等. 智能仓库中的多AGV协同路径规划方法[J]. 计算机集成制造系统, 2018, 24(2): 410-418.