|
|
|
发布时间: 2022-02-28 |
应用基础研究 |
|
|
|
收稿日期: 2021-05-12
基金项目: 国家自然科学基金(11801356)
中图法分类号: O153.3
文献标识码: A
文章编号: 2096-8299(2022)01-0094-04
|
摘要
零因子图主要是利用图论的语言和工具来研究并解决代数中的一些难题。对于任意的有限交换局部环, 其代数结构一直是研究难点。通过对零因子图团数的分类, 讨论了当团数为5时, 对应的有限交换局部环R的代数性质, 刻画了环R的极大理想 的幂零指数。特别是, 当极大理想
的幂零指数。特别是, 当极大理想 的幂零指数为5时, 对极大理想
的幂零指数为5时, 对极大理想 的代数结构及极小生成元集进行了具体刻画。
的代数结构及极小生成元集进行了具体刻画。
关键词
有限交换局部环; 星图加细; 代数结构; 团数
Abstract
In recent years, zero-divisor graph mainly uses the language and tools of graph theory to study and solve some research problems in algebra.For any finite local ring R, the algebraic structure of ring R is always a difficult problem.We study the algebraic properties of rings R whose zero-divisor graph Γ(R) has clique number five.Furthermore, we give the complete characterizations of the maximal ideal of the finite commutative local rings with ω(Γ(R))=5 and N( )=5.
)=5.
Key words
finite commutative local rings; refinements of a star graph; structure; clique number
零因子图是近年来一个新的研究领域, 主要研究环与半群的代数结构、性质与其零因子图的图结构、图性质之间的关联关系。零因子图的概念首先是由BECK I[1]在1988年提出的, 后来又有许多数学工作者对这一概念进行了研究和推广[2-8]。本文主要是利用零因子图的团数来研究相应的有限交换局部环(以下简称“有限局部环”)的代数结构与性质。
设(R, 





1 引理介绍
引理1 设(R, 

证明 令k=N(


因为
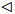









假设k≥6, 可知a2=b2=c2=ac=ab=bc=0。由(a+c)u=0, 可知a+c≠b。同理可证: a+b≠c, b+c≠a。
由此可知, 点集{a, b, c, a+c, a+b, b+c}构成完全图K6, 这与已知条件ω(Γ(R))=5矛盾。故假设不成立, 即N(
引理2 设(R, 

证明 反设Γ(R)至少有两个中心c和e, 则c

因为










2 主要结论
定理3 设(R, 

(1) 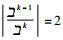
(2) 极大理想
证明 (1) 由已知条件及前面两个引理可知: 


易知, 




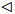



假设|







综上分析可知, 点集{a, c, a+c, b, b+c, t}构成完全图K6。这与已知矛盾, 故假设不成立。因此, |
不妨假设






假设b2=0。因为ab∈



由点b的取法可知, 点集{0, a, c, a+c, b, b+c, a+b, a+b+c}中的点两两互不相等, 且都包含在


反设|



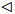

| $ \begin{array}{c} c=(b+d)^{2}=b^{2}+2 b d+d^{2}= \\ b^{2}+d^{2}+2 b d=2 c+2 b d \end{array} $ | (1) |
由引理2可知, Γ(R)是中心c的星图加细, 由中心的唯一性可知2c=0。故2∈


(2) 由(1)的证明, 不妨令



反设n≤2。若n=1, 即
令



下面分情况考虑α12和α22的值。
情况1 若α12=α22, 由上面的分析可知, α12和α22不能同时为0。
① 若α12=α22=b, 则α13=bα1, α23=bα2=α1(α1α2)。下面考虑α1α2的值。易知, α1α2∈
若α1α2=c, 则α13=α12α1=α22α1=α2(α2α1)=0。同理可证, α23=0。这与
若α1α2=a, 则α13=α12α1=α22α1=α2(α2α1)= aα2=0。同理可证, α23=aα1=c, α24=0。这与
若α1α2=b, 则α13=α12α1=α22α1=α2(α2α1)=α2b=α23, 又因为
若α13=α23=c, 则b2=(α12)2=α14=cα1=0。这与前面讨论中b2=c相矛盾, 故αi3不可能同时为c(i=1, 2)。
若α13=α23=a, 则b2=(bα1)α2=α13α2=aα2=0。根据类似上述的讨论可知, 假设不成立, 故αi3不可能同时为a。同理可证, αi3不可能同时为a+c。
由上述的讨论可知, αi3(i=1, 2)不可能同时为0, c, a, a+c。这与αi2∈
综上所述, α1α2≠0, c, a, a+c, b, b+c, a+b, a+b+c。这与α1α2∈
② 若α12=α22=a, 下面考虑α1α2的值。
若α1α2=c, 则c=aα1=α22α1=α2c=0。这与c不为0相矛盾, 故α1α2≠c。同理可证α1α2≠0。
若α1α2=a, 则α13=(α22)α1=aα1=c, α14=0, α23=aα2=0。由此可得, 

若α1α2=b, 则bα1=(α1α2)α1=aα2=0, c=b2=b(α1α2)=0。这与c不为0相矛盾, 故α1α2≠b。同理可证, α1α2≠b+c, a+b, a+b+c。
综上所述, α1α2≠0, c, a, a+c, b, b+c, a+b, a+b+c。这与α1α2∈
根据上述情况1的讨论可知, 情况1的前提假设不成立, 故α12≠α22。
先考虑α22的值。假设α22=b, 则α23=bα2∈
又因为α22∈
情况2 若α22=c, 考虑α12的值。若α12=a, 则α14=0, α23=0。由此可得, 

① 若α1α2=0, 则bα2=α12α2=α1(α1α2)=0, (b+α2)2=b2+2bα2+α22=0。
又因为a(b+α2)=0, 这与(1)中的证明相矛盾, 故α1α2≠0。同理可证, α1α2≠c。
② 若α1α2=a, 则bα2=α1(α1α2)=aα1=c, (b+α2)2=b2+2bα2+α22=c+2c+c=0。与上面的讨论类似, 可得出相矛盾。
③ 若α1α2=b, 则bα2=(α1α2)α2=α1α22=α1c=0。与上述的讨论类似, 可知假设不成立。由上面的分析可知, α22≠c。同理可证, α22≠0。
目前, 只剩下1种情况, 即α12=b, α22=a。此时, c=aα1=α22α1=α2(α2α1), 由α2α1∈


3 结语
本文讨论了当零因子图Γ(R)的团数是5, 并且极大理想


参考文献
-
[1]BECK I. Coloring of commutative rings[J]. Journal of Algebra, 1988, 116(1): 208-226. DOI:10.1016/0021-8693(88)90202-5
-
[2]ANDERSON D F, LEWIS E F. A general theory of zero-divisor graphs over a commutative ring[J]. International Electronic Journal of Algebra, 2016, 20(20): 111-135. DOI:10.24330/ieja.266187
-
[3]ANDERSON D F, LIVINGSTON P S. The zero-divisor graph of a commutative ring[J]. Journal of Algebra, 1999, 217(2): 434-447. DOI:10.1006/jabr.1998.7840
-
[4]HAOUAOUI A, BENHISSI A. Zero-divisors and zero-divisor graphs of power series rings[J]. Ricerche Di Matematica, 2016, 65(1): 1-13. DOI:10.1007/s11587-015-0235-y
-
[5]LIU Q, WU T S. On zero-divisor graphs whose cores contain no rectangles[J]. Algebra Colloquium, 2011, 18(4): 675-684. DOI:10.1142/S1005386711000526
-
[6]ANDERSON D F, FRAZIER A, LAUVE A, et al. The zero-divisor graph of a commutative ring Ⅱ[M]//ANDERSON D D, PAPICK I J. Ideal theoretic methods in commutative algebra. New York: CRC Press, 2001: 61-72.
-
[7]ZHURAVLEV E V, MONASTYREVA A S. Compressed zero-divisor graphs of finite associative rings[J]. Siberian Mathematical Journal, 2020, 61(1): 76-84.
-
[8]RAD N J, JAFARI S H. A characterization of bipartite zero-divisor graphs[J]. Canadian Mathematical Bulletin, 2014, 57(1): 188-193. DOI:10.4153/CMB-2013-011-6
-
[9]ATIYAH M F, MACDONALD I G. Introduction to commutative algebra[M]. Reading: Addison-Wesley, 1969: 36-50.
-
[10]BUCKLEY F, LEWINTER M. A friendly introduction to graph theory[M]. Upper Saddle River: Prentice-Hall, 2003: 23-53.




