|
|
|
发布时间: 2022-02-28 |
应用基础研究 |
|
|
|
收稿日期: 2021-11-06
基金项目: 国家自然科学基金青年项目(11601318)
中图法分类号: O221
文献标识码: A
文章编号: 2096-8299(2022)01-0098-07
|
摘要
提出了一种新的基于邻近梯度的对偶方法。该方法求解Frobenius范数意义下的相关系数矩阵的稀疏逼近问题。首先, 推导出一种新的有界约束的对偶问题; 然后, 提出一个相应的具有全局收敛性的邻近梯度算法; 最后, 通过在随机数据集上的数值结果验证了该算法的可行性。
关键词
相关系数矩阵; 稀疏逼近; 对偶邻近梯度算法; 全局收敛性
Abstract
In this paper, we propose a novel dual method based on proximal gradient method for the sparse approximation of correlation matrices in the sense of Frobenius norm.A new dual formulation with bound constraints is derived.To solve the dual, a global convergent proximal gradient algorithm is developed.Some preliminary numerical results on synthetic data sets are given to confirm the feasibility of our algorithm.
Key words
correlation matrices; sparse approximation; dual proximal gradient algorithm; global convergence
近年来, 利用半正定协方差矩阵的稀疏逼近在声纳数据处理[1]、细胞信号恢复[2]、基因聚类[3]、语音信号分类[4-5]等领域都有着广泛的应用。正如文献[6]提到的, 协方差矩阵不是尺度不变的。稀疏半正定相关系数矩阵在基因聚类的实际应用中也发挥着重要作用[6-7]。因此, 寻求一种新的、高效求解半正定相关系数矩阵稀疏逼近问题的算法是非常必要的。
CUI Y等人[6]首次提出采用对偶方法, 通过加速近端梯度来求解稀疏逼近问题的某种对偶问题。该方法是对已被广泛研究的协方差矩阵稀疏逼近[1-5]的推广。本文针对稀疏逼近优化问题推导出一个新的对偶问题, 并利用邻近梯度法求解该新对偶问题。
本文首先将引入稀疏逼近优化问题的一个新对偶, 并给出一阶最优性条件; 然后提出一种新的基于近邻梯度的对偶方法来求解所得到的新对偶问题, 并证明其具有全局收敛性; 最后通过数值对比验证了该算法的有效性。
1 对偶问题及其最优性条件
1.1 稀疏逼近优化问题
本文主要考虑如下形式的稀疏优化问题
| $ \begin{gathered} \min \frac{1}{2}\|\boldsymbol{X}-\boldsymbol{C}\|_{\mathrm{F}}^{2}+|\boldsymbol{P} \circ \boldsymbol{X}|_{1} \\ \text { s. t. }\left\langle\boldsymbol{A}_{i}, \boldsymbol{X}\right\rangle=b_{i}, \\ \left\langle\boldsymbol{B}_{j}, \boldsymbol{X}\right\rangle \leqslant u_{j}, \\ \boldsymbol{X}-\epsilon I \in S_{+}^{n} \end{gathered} $ | (1) |
其中: C∈Sn; Ai, Bj∈Sn; bi, uj∈ R; i∈
若对于矩阵P中某些元素, Pij=0, 那么对Xij不要求具有稀疏性。若要求矩阵X的对角线元素为1, 即定义Ai的第s行第t列中的元素为
| $ \left[\boldsymbol{A}_{i}\right]_{s t}=\left\{\begin{array}{l} 1, s=t=i \\ 0, \text { 其他 } \end{array}\right. $ | (2) |
其中: s=1, 2, 3, …, n; t=1, 2, 3, …, n。b的第i个元素bi=1, i=1, 2, 3, …, n。则可以得到式(1)模型的一个特例, 即具有以下形式的相关系数矩阵的稀疏逼近:
| $ \begin{gathered} \min \frac{1}{2}\|\boldsymbol{X}-\boldsymbol{C}\|_{\mathrm{F}}^{2}+|\boldsymbol{P} \circ \boldsymbol{X}|_{1} \\ \text { s. t. } X_{i i}=1, i \in[n], \\ \boldsymbol{X}- {\mathit{\pmb{\epsilon}}} \boldsymbol{I} \in S_{+}^{n} \end{gathered} $ | (3) |
其中: [n]表示集合{1, 2, 3, …, n}。
在引入问题式(1)的新对偶之前, 先定义线性映射A: Sn→R|
| $ \begin{aligned} \boldsymbol{A}(\boldsymbol{X}) &=\left[\begin{array}{l} \left\langle\boldsymbol{A}_{1}, \boldsymbol{X}\right\rangle \\ \left\langle\boldsymbol{A}_{2}, \boldsymbol{X}\right\rangle \\ \left\langle\boldsymbol{A}_{3}, \boldsymbol{X}\right\rangle \\ \vdots \\ \left\langle\boldsymbol{A}_{|\mathcal{E}|}, \boldsymbol{X}\right\rangle \end{array}\right], \\ \boldsymbol{B}(\boldsymbol{X}) &=\left[\begin{array}{l} \left\langle\boldsymbol{B}_{1}, \boldsymbol{X}\right\rangle \\ \left\langle\boldsymbol{B}_{2}, \boldsymbol{X}\right\rangle \\ \left\langle\boldsymbol{B}_{3}, \boldsymbol{X}\right\rangle \\ \vdots \\ \left\langle\boldsymbol{B}_{|\mathcal{I}|}, \boldsymbol{X}\right\rangle \end{array}\right] \end{aligned} $ | (4) |
其中: |
| $ \begin{gathered} \min \frac{1}{2}\|\boldsymbol{X}-\boldsymbol{C}\|_{\mathrm{F}}^{2}+|\boldsymbol{P} \circ \boldsymbol{X}|_{1} \\ \text { s. t. } \boldsymbol{A}(\boldsymbol{X})=\boldsymbol{b}, \boldsymbol{B}(\boldsymbol{X}) \leqslant \boldsymbol{u}, \\ \boldsymbol{X}-{{\mathit{\pmb{\epsilon}}}} \boldsymbol{I} \in S_{+}^{n} \end{gathered} $ | (5) |
其中: b=[b1, b2, b3, …, b|
于是, 在式(3)中, A(X)=diag(X), |
1.2 一个新的对偶问题
根据文献[8], 考虑问题式(5)的广义拉格朗日函数为
记C=C+Λ+A*(γ)-B*(λ)。A*, B*分别表示A, B的伴随算子, 具体形式为A*(γ)=
经过计算可得问题式(5)的对偶问题如下
| $ \begin{aligned} \min\ & \varPsi(\boldsymbol{\varLambda}, \boldsymbol{\gamma}, \boldsymbol{\lambda})=\\ & \frac{1}{2}\left\|\left(\boldsymbol{C}+\boldsymbol{\varLambda}+\boldsymbol{A}^{*}(\boldsymbol{\gamma})-\boldsymbol{B}^{*}(\boldsymbol{\lambda})- {\mathit{\pmb{\epsilon}}} \boldsymbol{I}\right)+\right\|_{\mathrm{F}}^{2}+\\ & {\mathit{\pmb{\epsilon}}}\left\langle\boldsymbol{A}(\boldsymbol{I})-\frac{\boldsymbol{b}}{{{\mathit{\pmb{\epsilon}}}}}, \boldsymbol{\gamma}\right\rangle, \boldsymbol{\gamma}-{{\mathit{\pmb{\epsilon}}}}\left\langle\boldsymbol{B}(\boldsymbol{I})-\frac{\boldsymbol{u}}{{\mathit{\pmb{\epsilon}}}}, \boldsymbol{\lambda}\right\rangle+\\ & {{\mathit{\pmb{\epsilon}}}}\langle\boldsymbol{\varLambda}, \boldsymbol{I}\rangle \\ & \text {s. t. }(\boldsymbol{\varLambda}, \boldsymbol{\lambda}) \in \varOmega \end{aligned} $ | (6) |
其中: Ω是可行集, 即
| $ \begin{aligned} \boldsymbol{\varOmega}=&\left\{(\boldsymbol{\varLambda}, \boldsymbol{\lambda}) \in S^{n} \times {\bf{R}}^{|\tau|} \mid-\boldsymbol{P} \leqslant\right.\\ &\boldsymbol{\varLambda} \leqslant \boldsymbol{P}, \boldsymbol{\lambda} \geqslant \boldsymbol{o}\} \end{aligned} $ | (7) |
注意到对偶问题式(6)中的目标函数Ψ(Λ, γ, λ)是凸的、连续可微的[9], 且当Slater约束条件满足时, 还是强制的[10-11](即当‖Λ‖F→∞或‖γ‖→∞, ‖λ‖→∞时, Ψ(Λ, γ, λ)→∞)。此外, 对偶目标函数Ψ(Λ, γ, λ)关于Λ, γ, λ的梯度分别为
| $ \begin{aligned} \nabla_{\boldsymbol{\varLambda}} \varPsi(\boldsymbol{\varLambda}, \boldsymbol{\gamma}, \boldsymbol{\lambda})=&\left(\boldsymbol{C}+\boldsymbol{A}^{*}(\boldsymbol{\gamma})-\boldsymbol{B}^{*}(\boldsymbol{\lambda})+\right.\\ &\boldsymbol{\varLambda}-{\mathit{\pmb{\epsilon}}} \boldsymbol{I})_{+}+{\mathit{\pmb{\epsilon}}} \boldsymbol{I} \\ \nabla_{\boldsymbol \gamma} \varPsi(\boldsymbol{\varLambda}, \boldsymbol{\gamma}, \boldsymbol{\lambda})=& \boldsymbol{A}\left(\boldsymbol{C}+\boldsymbol{A}^{*}(\boldsymbol{\gamma})-\boldsymbol{B}^{*}(\boldsymbol{\lambda})+\right.\\ &\boldsymbol{\varLambda}-{\mathit{\pmb{\epsilon}}} \boldsymbol{I})_{+}+{{\mathit{\pmb{\epsilon}}}} \boldsymbol{A}(\boldsymbol{I})-\boldsymbol{b}\\ \nabla_{\boldsymbol{\lambda}} \varPsi(\boldsymbol{\varLambda}, \boldsymbol{\gamma}, \boldsymbol{\lambda})=& \boldsymbol{B}\left(\boldsymbol{C}+\boldsymbol{A}^{*}(\boldsymbol{\gamma})-{{\mathit{\pmb{\epsilon}}}} \boldsymbol{B}^{*}(\boldsymbol{\lambda})+\right.\\ &\left.\boldsymbol{\varLambda}-{{\mathit{\pmb{\epsilon}}}} \boldsymbol{I})+{{\mathit{\pmb{\epsilon}}}}_{+} \boldsymbol{B}(\boldsymbol{I})+\boldsymbol{u}\right) \end{aligned} $ | (8) |
式(8)中的梯度都是Lipschitz连续的, 且当Slater约束规范条件成立时, 问题式(5)和对偶问题式(6)之间的对偶间隙为零。从而, 只需求解对偶问题式(6)即可。
1.3 最优性条件
由于不等式约束-Pij≤Λij≤Pij, i, j∈[n], λ≥ o的特殊结构, Mangasarian-Fromovitz约束规范条件在对偶问题式(6)的任意可行点都成立[12], 于是可以得到对偶问题式(6)的一阶最优性条件。
引理1 若(Λ*, γ*, λ*)是对偶问题式(6)的最优解, 则存在Θ1*∈Sn, Θ2*∈Sn, Θ3*∈R|
| $ \left\{\begin{array}{l} \nabla_{\boldsymbol{\varLambda}}\left(\boldsymbol{\varLambda}^{*}, \boldsymbol{\gamma}^{*}, \boldsymbol{\lambda}^{*}\right)-\boldsymbol{\varTheta}_{1}^{*}+\boldsymbol{\varTheta}_{2}^{*}=\boldsymbol{O} \\ \nabla_{\boldsymbol \gamma}\left(\boldsymbol{\varLambda}^{*}, \boldsymbol{\gamma}^{*}, \boldsymbol{\lambda}^{*}\right)=\boldsymbol{O} \\ \nabla_{\boldsymbol \lambda}\left(\boldsymbol{\varLambda}^{*}, \boldsymbol{\gamma}^{*}, \boldsymbol{\lambda}^{*}\right)-\boldsymbol{\varTheta}_{3}^{*}=\boldsymbol{o} \\ \boldsymbol{\varTheta}_{1}^{*} \circ\left(\boldsymbol{\varLambda}^{*}+\boldsymbol{P}\right)=\boldsymbol{O} \\ \boldsymbol{\varTheta}_{2}^{*} \circ\left(\boldsymbol{\varLambda}^{*}-\boldsymbol{P}\right)=\boldsymbol{O} \\ \left\langle\boldsymbol{\lambda}^{*}, \boldsymbol{\varTheta}_{3}^{*}\right\rangle=\boldsymbol{o} \\ -\boldsymbol{P} \leqslant \boldsymbol{\varLambda}^{*} \leqslant \boldsymbol{P}, \boldsymbol{\varTheta}_{1}^{*} \geqslant \boldsymbol{O}, \boldsymbol{\varTheta}_{2}^{*} \geqslant \boldsymbol{O} \\ \ \ \ \ \boldsymbol{\varTheta}_{3}^{*} \geqslant \boldsymbol{o}, \boldsymbol{\lambda}^{*} \geqslant \boldsymbol{o} \end{array}\right. $ | (9) |
称引理1中的Θ1*和Θ2*为最优乘子矩阵, Θ3*为最优乘子向量。若数组(Λ*, γ*, λ*, Θ1*, Θ2*, Θ3*)满足式(9), 则称其为KKT数组, 称(Λ*, γ*, λ*)为KKT点。为了方便起见, 用‖(Λ, λ)‖F表示
| $ r\left(\boldsymbol{\varLambda}^{k}, \boldsymbol{\gamma}^{k}, \boldsymbol{\lambda}^{k}\right)=\frac{\max \left\{\left\|\left(\boldsymbol{\varLambda}^{k}, \boldsymbol{\lambda}^{k}\right)-\Pi_{\varOmega}\left(\overline{\boldsymbol{\varLambda}}{}^{k}, \overline{\boldsymbol{\lambda}}{}^{k}\right)\right\|_{\mathrm{F}},\left\|\nabla_{\boldsymbol\gamma} \varPsi\left(\boldsymbol{\varLambda}^{k}, \boldsymbol{\gamma}^{k}, \boldsymbol{\lambda}^{k}\right)\right\|\right\}}{1+\left\|\boldsymbol{\varLambda}^{k}\right\|_{\mathrm{F}}+\left\|\boldsymbol{\gamma}^{k}\right\|+\left\|\boldsymbol{\lambda}^{k}\right\|} $ | (10) |
其中:
| $ \left[\boldsymbol{P}_{Y}\right]_{i j}=\left\{\begin{array}{l} -P_{i j}, \text { 当 } Y_{i j}<-P_{i j} \\ P_{i j}, \text { 当 } Y_{i j}>P_{i j}, \\ Y_{i j}, \text { 其他 } \end{array}\ \ i, j \in[n]\right. $ | (11) |
| $ \left[\boldsymbol{P_{Z}}\right]_{j}=\left\{\begin{array}{l} 0, \text { 当 } Z_{j}<0, \\ Z_{j}, \text { 当 } Z_{j} \geqslant 0, \end{array},j\in \mathcal{I}\right. $ | (12) |
此外, 容易验证一阶最优性条件式(9)等价于
| $ r\left(\boldsymbol{\varLambda}^{k}, \boldsymbol{\gamma}^{k}, \boldsymbol{\lambda}^{k}\right)=0 $ | (13) |
因此, KKT误差rk=r(Λk, γk, λk)可以用来度量最优性。
2 一种新的对偶方法及其收敛性分析
本节将应用邻近梯度法求解对偶问题式(6)。
2.1 求解对偶问题的邻近梯度法
邻近梯度法[13]一般用于求解可分解的、非光滑的无约束优化问题, 即
| $ \min f_{1}(x)+f_{2}(x) $ | (14) |
其中: f1是凸的且可微的; f2是凸的邻近映射(但不一定是可微的)。在当前迭代点, 邻近梯度法的迭代公式为
| $ x^{k+1}=\operatorname{prox}_{\alpha^{k} f_{2}}\left(x^{k}-\alpha^{k} \nabla f_{1}\left(x^{k}\right)\right) $ | (15) |
其中: αk>0是步长。
针对问题式(5), 核心是计算邻近梯度方向作为搜索方向。具体地说, 在点(Λk, γk, λk), 可以分别通过求解子问题得到搜索方向(DΛk, dγk)∈Sn×R|
| $ \begin{aligned} &\min \left\langle\nabla_{\boldsymbol{\varLambda}} \varPsi\left(\boldsymbol{\varLambda}^{k}, \boldsymbol{\gamma}^{k}, \boldsymbol{\lambda}^{k}\right), \boldsymbol{\varLambda}^{k}+\boldsymbol{D}_{\boldsymbol{\varLambda}}\right\rangle+ \\ &\left\langle\nabla_{\boldsymbol{\lambda}} \varPsi\left(\boldsymbol{\varLambda}^{k}, \boldsymbol{\gamma}^{k}, \boldsymbol{\lambda}^{k}\right), \boldsymbol{\lambda}^{k}+\boldsymbol{d}_{\boldsymbol{\lambda}}\right\rangle+\frac{1}{2}\left\|\boldsymbol{D}_{\boldsymbol{\varLambda}}\right\|_{\mathrm{F}}^{2}+ \\ &\frac{1}{2}\left\|\boldsymbol{d}_{\boldsymbol{\lambda}}\right\|_{\mathrm{F}}^{2}+\delta_{\varOmega}\left(\boldsymbol{\varLambda}^{k}+\boldsymbol{D}_{\boldsymbol{\varLambda}}, \boldsymbol{\lambda}^{k}+\boldsymbol{d}_{\boldsymbol{\lambda}}\right) \end{aligned} $ | (16) |
| $ \min \nabla_{\boldsymbol\gamma} \varPsi\left(\boldsymbol{\varLambda}^{k}, \boldsymbol{\gamma}^{k}, \boldsymbol{\lambda}^{k}\right)^{\mathrm{T}} \boldsymbol{d}_{\boldsymbol\gamma}+\frac{1}{2}\left\|\boldsymbol{d}_{\boldsymbol\gamma}\right\|^{2} $ | (17) |
其中: δΩ(Λ, λ)是Ω的指示函数, 即
| $ \delta_{\varOmega}(\boldsymbol{\varLambda}, \boldsymbol{\lambda})=\left\{\begin{array}{l} 0,(\boldsymbol{\varLambda}, \boldsymbol{\lambda}) \in \varOmega \\ \infty, \text { 其他 } \end{array}\right. $ | (18) |
注意到式(16)中目标函数的前4项是连续可微的, 最后1项是凸函数, 其邻近映射可由式(19)计算得到
| $ \begin{gathered} \operatorname{prox}_{\delta_{\varOmega}}\left(\boldsymbol{\varLambda}^{k}+\boldsymbol{D}_{\boldsymbol{\varLambda}}, \boldsymbol{\lambda}^{k}+\boldsymbol{d}_{\boldsymbol{\lambda}}\right)= \\ \Pi_{\varOmega}\left(\boldsymbol{\varLambda}^{k}+\boldsymbol{D}_{\boldsymbol{\varLambda}}, \boldsymbol{\lambda}^{k}+\boldsymbol{d}_{\boldsymbol{\lambda}}\right) \end{gathered} $ | (19) |
其中:
ΠΩ(·)由式(11)计算可得。容易推出式(16)和式(17)闭合形式的解分别如下
| $ \begin{aligned} \left(\boldsymbol{D}_{\boldsymbol{\varLambda}}^{k}, \boldsymbol{d}_{\lambda}^{k}\right)=& \Pi_{\varOmega}\left(\boldsymbol{\varLambda}^{k}-\nabla_{\boldsymbol{\varLambda}} \varPsi\left(\boldsymbol{\varLambda}^{k}, \boldsymbol{\gamma}^{k}, \boldsymbol{\lambda}^{k}\right),\right.\\ &\left.\boldsymbol{\lambda}^{k}-\nabla_{\boldsymbol\lambda} \varPsi\left(\boldsymbol{\varLambda}^{k}, \boldsymbol{\gamma}^{k}, \boldsymbol{\lambda}^{k}\right)\right)-\\ &\left(\boldsymbol{\varLambda}^{k}, \boldsymbol{\lambda}^{k}\right) \end{aligned} $ | (20) |
| $ \boldsymbol{d}_{\boldsymbol\gamma}^{k}=-h\left(\boldsymbol{\varLambda}^{k}, \boldsymbol{\gamma}^{k}\right) $ | (21) |
DΛk, dλk和dγk为投影梯度步, 对算法的全局收敛性起着重要作用。
2.2 主要算法
下面将给出完整的对偶邻近梯度算法(Dual Proximal Gradient Algorithm, DPGA)。令(Λk, γk, λk)为当前迭代点, 通过式(16)和式(17)(或式(20)和式(21))可得邻近梯度步。定义Ψ(Λ, γ, λ)的预计线性下降量Δk为
| $ \begin{aligned} \varDelta^{k}=&\left\langle\nabla_{\boldsymbol{\varLambda}} \varPsi\left(\boldsymbol{\varLambda}^{k}, \boldsymbol{\gamma}^{k}, \boldsymbol{\lambda}^{k}\right), \boldsymbol{D}_{\boldsymbol{\varLambda}}^{k}\right\rangle+\\ &\left\langle\nabla_{\boldsymbol\gamma} \varPsi\left(\boldsymbol{\varLambda}^{k}, \boldsymbol{\gamma}^{k}, \boldsymbol{\lambda}^{k}\right), \boldsymbol{d}_{\boldsymbol\gamma}^{k}\right\rangle+\\ &\left\langle\nabla_{\boldsymbol{\lambda}} \varPsi\left(\boldsymbol{\varLambda}^{k}, \boldsymbol{\gamma}^{k}, \boldsymbol{\lambda}^{k}\right), \boldsymbol{d}_{\boldsymbol{\lambda}}^{k}\right\rangle \end{aligned} $ | (22) |
利用线搜索回溯技术, 在{1, τ, τ2, …}中寻找最大的αk, 使得Ψ(Λ, γ, λ)满足充分下降条件
| $ \begin{gathered} \varPsi\left(\Pi_{\varOmega}\left(\boldsymbol{\varLambda}^{k}+\alpha^{k} \boldsymbol{D}_{\boldsymbol{\varLambda}}^{k}, \boldsymbol{\gamma}^{k}+\alpha^{k} \boldsymbol{d}_{\boldsymbol\gamma}^{k}\right), \boldsymbol{\lambda}^{k}+\alpha^{k} \boldsymbol{d}_{\boldsymbol{\lambda}}^{k}\right) \leqslant \\ \varPsi\left(\boldsymbol{\varLambda}^{k}, \boldsymbol{\gamma}^{k}, \boldsymbol{\lambda}^{k}\right)+\sigma \alpha^{k} \varDelta^{k} \end{gathered} $ | (23) |
其中: τ∈(0, 1);σ∈(0, 1)是给定的常数。从而, 可得DPGA算法的迭代公式为
| $ \begin{gathered} \boldsymbol{\varLambda}^{k+1} =\boldsymbol{\varLambda}^{k}+\alpha^{k} \boldsymbol{D}_{\boldsymbol{\varLambda}}^{k}, \\ \boldsymbol{\gamma}^{k+1} =\boldsymbol{\gamma}^{k}+\alpha^{k} \boldsymbol{d}_{\boldsymbol\gamma}^{k} ,\\ \boldsymbol{\lambda}^{k+1} =\boldsymbol{\lambda}^{k}+\alpha^{k} \boldsymbol{d}_{\boldsymbol{\lambda}}^{k} \end{gathered} $ | (24) |
对于算法的终止条件, 将类似于文献[6], 用ηgap来表示原始-对偶的间隙, 可以衡量原始目标与对偶目标函数值之间的差异, 即
| $ \eta_{\mathrm{gap}}=\frac{\left|j_{\mathrm{prob}}-j_{\mathrm{dob}}\right|}{1+\left|j_{\mathrm{prob}}\right|+\left|j_{\mathrm{dob}}\right|} $ | (25) |
其中: jprob和jdob分别表示原始目标函数值和对偶目标函数值。
当式(26)成立时, DPGA算法停止。
| $ \max \left(r^{k}, \eta_{\mathrm{gap}}^{k}\right) \leqslant \varepsilon $ | (26) |
其中: ε>0是给定的误差; rk是式(10)中定义的残差; ηgapk是在点(Λk, γk, λk)处的间隙。
定理1 由DPGA算法生成的序列{(Λk, γk, λk)}的任何聚点都是对偶问题式(6)的最优解。
证明: 应用邻近梯度方法收敛性结论立即可得到所提算法的全局收敛性。
3 数值实验
为了验证DPGA算法的有效性, 本文将其与文献[6]中的相关系数矩阵稀疏估计(Sparse Estimation of the Correlation matrix, SEC)算法进行了比较。为了公平比较, 本文还将SEC算法代码中的EIG(·)替换为Mexeig(·)。
3.1 设置问题
本文实验中的测试问题形式如下
| $ \begin{gathered} \min \frac{1}{2}\|\boldsymbol{X}-\boldsymbol{C}\|_{\mathrm{F}}^{2}+\rho|\boldsymbol{W} \circ \boldsymbol{X}|_{1} \\ \text { s. t. } X_{i i}=1, i \in[n] ,\\ \boldsymbol{X}-{\mathit{\pmb{\epsilon}}} \boldsymbol{I} \in S_{+}^{n} \end{gathered} $ | (27) |
其中: ϵ>0用于保证X的正定性; ρ>0是正则化参数; W∈Sn是一个权重矩阵。注意, 当P=ρW时, 问题式(3)与问题式(27)相同。这里, 选择权重矩阵W作为经典的l1惩罚[6]。
取ε=10-6。当DPGA算法满足终止条件式(26), 或达到最大迭代次数(5 000次)时停止。DPGA算法中的其他参数设置如下: Λ0=O, γ0=o, σ=10-4, τ=0.5。此外, SEC算法采用默认参数。
3.2 合成数据集
本文生成矩阵C有以下两种方法。
(1) 测试问题E1 式(27)中的矩阵C由MATLAB命令实现生成。具体为: C=rand(n, n); C=(C+C′)/2;C(1:n+1:end)=1。
(2) 测试问题E2 式(27)中的矩阵C是一个样本相关系数矩阵, 是由一组N(0, Σ)样本计算生成的, 均值为零。其中: Σ是一个的n×n的协方差矩阵。特别地, 定义
| $ \begin{gathered} \boldsymbol{\varSigma}_{i j}=\max \left(0,\left(1-\frac{|i-j|}{10}\right)\right), \\ i, j \in[n] \end{gathered} $ | (28) |
接下来, 将从N(0, Σ)中抽取p个独立同分布的样本, 用D∈ Rp×n来表示。最后, 应用zscore方法对D进行归一化, 使得每个特征的均值为零, 单位方差为1。在归一化数据上, 样本协方差矩阵与样本相关系数矩阵相同。在本文的数值实验中, 对所有给定的矩阵C, ρ=0.01, 将通过求解式(27)来估计相关系数矩阵。
本文从式(27)对偶问题的残差、CPU时间、总迭代次数、原始目标值, 以及估计的相关系数矩阵的稀疏性等5个方面与算法SEC进行比较。实验结果表明, SEC算法和DPGA算法都能在预设误差小于10-6和最大迭代次数内成功地解决所有测试问题。
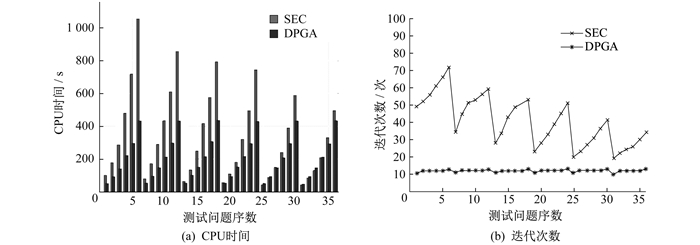
图 1显示了SEC和DPGA算法在E1上的数值结果。其中, ϕ和ϕmin分别为目标函数值和其最小值。由图 1(a)可以看出, 在n∈[1 000, 2 800]之间所有10个测试问题上, 尽管差距很小, 但DPGA算法得到的原始目标值都优于SEC算法。对于残差, 图 1(b)显示DPGA算法在所有情况下都比SEC算法更精确。此外, 由图 1(c)和图 1(d)可以看出, DPGA算法在E1上的迭代次数不仅小于SEC算法的1/4, 而且CPU时间也少了一半, 这说明本文所提出的DPGA算法更具优越性。
此外, 通过设置n∈[1 000, 2 000]和样本数p∈[1 000, 2 000], 对E2进行了实验研究。图 2和表 1给出了E2的相关数值结果。由图 2可以看出, 与SEC算法相比, DPGA算法在E2上几乎都能以更少的迭代次数获得更高精度的解。从表 1可以观察到, SEC和DPGA算法在E2上都可以达到几乎相同的原始目标值及相同的稀疏程度。
表 1
E2上的数值结果
| n | p | SEC算法 | DPGA算法 | |||||
| 残差 | 原始目标值 | 稀疏程度 | 残差 | 原始目标值 | 稀疏程度 | |||
| 1 000 | 1 000 | 9.24×10-7 | 288.26 | 7.77×105 | 7.17×10-7 | 288.26 | 8.67×105 | |
| 1 200 | 1 000 | 8.90×10-7 | 397.09 | 1.13×106 | 1.87×10-7 | 397.09 | 1.13×106 | |
| 1 400 | 1 000 | 9.20×10-7 | 528.12 | 1.55×106 | 3.21×10-7 | 528.12 | 1.60×106 | |
| 1 600 | 1 000 | 8.83×10-7 | 668.89 | 2.03×106 | 5.58×10-7 | 668.89 | 2.23×106 | |
| 1 800 | 1 000 | 9.42×10-7 | 824.63 | 2.58×106 | 8.75×10-7 | 824.63 | 2.95×106 | |
| 2 000 | 1 000 | 9.86×10-7 | 1 005.08 | 3.20×106 | 6.69×10-7 | 1 005.08 | 3.55×106 | |
| 1 000 | 1 200 | 9.93×10-7 | 268.44 | 7.54×105 | 6.18×10-7 | 268.44 | 8.29×105 | |
| 1 200 | 1 200 | 9.51×10-7 | 369.79 | 1.09×106 | 1.69×10-7 | 369.79 | 1.10×106 | |
| 1 400 | 1 200 | 6.61×10-7 | 482.97 | 1.50×106 | 3.35×10-7 | 482.97 | 1.55×106 | |
| 1 600 | 1 200 | 7.81×10-7 | 614.09 | 1.96×106 | 5.18×10-7 | 614.09 | 2.14×106 | |
| 1 800 | 1 200 | 9.23×10-7 | 759.03 | 2.50×106 | 7.88×10-7 | 759.03 | 2.87×106 | |
| 2 000 | 1 200 | 9.77×10-7 | 921.22 | 3.10×106 | 5.98×10-7 | 921.22 | 3.43×106 | |
| 1 000 | 1 400 | 8.84×10-7 | 252.02 | 7.33×105 | 5.90×10-7 | 252.02 | 8.06×105 | |
| 1 200 | 1 400 | 9.70×10-7 | 346.86 | 1.06×106 | 1.72×10-7 | 346.86 | 1.07×106 | |
| 1 400 | 1 400 | 8.86×10-7 | 455.79 | 1.46×106 | 2.78×10-7 | 455.79 | 1.49×106 | |
| 1 600 | 1 400 | 9.72×10-7 | 569.54 | 1.90×106 | 5.01×10-7 | 569.54 | 2.08×106 | |
| 1 800 | 1 400 | 8.31×10-7 | 703.52 | 2.42×106 | 7.63×10-7 | 703.52 | 2.80×106 | |
| 2 000 | 1 400 | 7.90×10-7 | 849.56 | 3.00×106 | 5.82×10-7 | 849.56 | 3.33×106 | |
| 1 000 | 1 600 | 8.08×10-7 | 242.61 | 7.14×105 | 5.64×10-7 | 242.61 | 7.80×105 | |
| 1 200 | 1 600 | 7.67×10-7 | 326.60 | 1.03×106 | 1.69×10-7 | 326.60 | 1.04×106 | |
| 1 400 | 1 600 | 9.10×10-7 | 426.14 | 1.41×106 | 3.01×10-7 | 426.14 | 1.45×106 | |
| 1 600 | 1 600 | 8.87×10-7 | 535.53 | 1.85×106 | 4.93×10-7 | 535.53 | 2.01×106 | |
| 1 800 | 1 600 | 8.76×10-7 | 657.09 | 2.35×106 | 7.48×10-7 | 657.09 | 2.73×106 | |
| 2 000 | 1 600 | 3.10×10-7 | 793.03 | 2.91×106 | 6.12×10-7 | 793.03 | 3.26×106 | |
| 1 000 | 1 800 | 9.87×10-7 | 228.78 | 6.92×105 | 6.36×10-7 | 228.78 | 7.65×105 | |
| 1 200 | 1 800 | 9.22×10-7 | 310.88 | 1.01×106 | 1.59×10-7 | 310.88 | 1.01×106 | |
| 1 400 | 1 800 | 8.79×10-7 | 404.45 | 1.37×106 | 3.01×10-7 | 404.45 | 1.40×106 | |
| 1 600 | 1 800 | 8.97×10-7 | 503.11 | 1.79×106 | 5.13×10-7 | 503.11 | 1.97×106 | |
| 1 800 | 1 800 | 9.83×10-7 | 625.47 | 2.30×106 | 7.38×10-7 | 625.47 | 2.67×106 | |
| 2 000 | 1 800 | 9.57×10-7 | 752.27 | 2.84×106 | 5.69×10-7 | 752.27 | 3.16×106 | |
| 1 000 | 2 000 | 5.95×10-7 | 220.41 | 6.76×105 | 9.86×10-7 | 220.41 | 8.28×105 | |
| 1 200 | 2 000 | 9.26×10-7 | 298.12 | 9.79×105 | 1.63×10-7 | 298.12 | 9.81×105 | |
| 1 400 | 2 000 | 6.63×10-7 | 381.62 | 1.33×106 | 3.08×10-7 | 381.62 | 1.36×106 | |
| 1 600 | 2 000 | 9.97×10-7 | 483.11 | 1.75×106 | 4.84×10-7 | 483.11 | 1.90×106 | |
| 1 800 | 2 000 | 9.47×10-7 | 595.84 | 2.24×106 | 7.14×10-7 | 595.84 | 2.60×106 | |
| 2 000 | 2 000 | 8.17×10-7 | 713.57 | 2.77×106 | 5.71×10-7 | 713.57 | 3.08×106 | |
综上所述, 针对本文所提出的新对偶问题式(6), DPGA算法可以较低的计算量获得相关系数矩阵稀疏逼近的最优解。
4 结语
本文提出了一种Frobenius范数下稀疏矩阵逼近问题的对偶邻近梯度算法, 用于求解由原始问题导出的一种新的对偶问题。该算法利用邻近梯度产生搜索方向, 并使用线搜索技术来寻找合适的步长以确保算法具有全局收敛性。此外, 本文还对相关模型随机生成数据进行了初步的数值实验, 并与文献[6]中的SEC算法进行了比较。通过对数值结果比较, 结果显示本文提出的求解对偶问题的DPGA算法优于SEC算法。
参考文献
-
[1]BOYD S, XIAO L. Least-squares covariance matrix adjustment[J]. SIAM Journal on Matrix Analysis & Applications, 2005, 27(2): 532-546.
-
[2]BIEN J. Sparse estimation of a covariance matrix[J]. Biometrika, 2011, 98(4): 807-820. DOI:10.1093/biomet/asr054
-
[3]CAI T, LIU W. Adaptive thresholding for sparse covariance matrix estimation[J]. Journal of the American Statistical Association, 2011, 106: 672-684. DOI:10.1198/jasa.2011.tm10560
-
[4]ROTHMAN J. Positive definite estimators of large covariance matrices[J]. Biometrika, 2012, 99(3): 733-740. DOI:10.1093/biomet/ass025
-
[5]LIU H, WANG L, ZHAO T. Sparse covariance matrix estimation with eigenvalue constraints[J]. Journal of Computational and Graphical Statistics, 2014, 23(2): 439-459. DOI:10.1080/10618600.2013.782818
-
[6]CUI Y, LENG C L, SUN D F. Sparse estimation of high-dimensional correlation matrices[J]. Computational Statistics and Data Analysis, 2016, 93: 390-403. DOI:10.1016/j.csda.2014.10.001
-
[7]SERRA A, CORETTO P, FRATELLO M, et al. Robust and sparse correlation matrix estimation for the analysis of high-dimensional genomics data[J]. Bioinformatics, 2018, 34(4): 625-634. DOI:10.1093/bioinformatics/btx642
-
[8]SHEN C G, XUE W J, ZHANG L H, et al. An active-set proximal Newton algorithm for regularized optimization problems with box constraints[J]. Journal of Scientific Computing, 2020, 85(3): 57. DOI:10.1007/s10915-020-01364-0
-
[9]BORWEIN J M, LEWIS A S. Partially finite convex programming, part Ⅱ: explicit lattice models[J]. Mathematical Programming, 1992, 57: 49-83. DOI:10.1007/BF01581073
-
[10]QI H D, SUN D F. A quadratically convergent Newton method for computing the nearest correlation matrix[J]. SIAM Journal on Matrix Analysis and Applications, 2006, 28(2): 360-385. DOI:10.1137/050624509
-
[11]ROCKAFELLAR T. Conjugate duality and optimization[M]. Philadelphia: Society for Industrial and Applied Mathematics, 1974.
-
[12]NOCEDAL J, WRIGHT S. Numerical optimization[M]. 2nd ed. New York: Springer, 2006.
-
[13]NESTEROV Y. Introductory lectures on convex optimization: a basic course[M]. New York: Springer, 2004.