|
|
|
发布时间: 2022-06-25 |
清洁安全发电 |
|
|
|
收稿日期: 2021-03-04
中图法分类号: TK11
文献标识码: A
文章编号: 2096-8299(2022)03-0227-07
|
摘要
为缓解国家电网压力, 根据国家民用建筑供暖标准, 设计了3种不同结构的固体蓄热装置。用数值模拟的方法研究了不同结构对蓄热装置放热特性的影响。结果表明, 在蓄热体总体积一定的情况下, 2块长方体蓄热体所在的正方体框内的空气温度最高, 其次是2块球形蓄热体所在的正方体, 而1块球形蓄热体所在的正方体框内的空气温度最低。
关键词
固体蓄热装置; 放热特性; 数值模拟
Abstract
In order to reduce the pressure of national state power grid, responding to the offpeak electricity utilization policy, solid regenerative devices with three different kinds of structures are designed according to the national civil building heating standard.The influence of different kinds of structures on the heat dissipation characteristics of the solid regenerative device is studied by the method of numerical simulation.The results show that when the total volume of heat accumulators is constant, the air temperature in the cube with two cubic heat accumulators is the highest, followed by two spherical heat accumulators.The air temperature in the cube with one spherical heat accumulator is the lowest.
Key words
solid regenerative device; heat dissipation characteristics; numerical simulation
由于地理位置的特殊性, 我国北方地区冬季寒冷, 供暖周期长。尤其是农村地区, 采用传统的火炕、土暖气、火炉等供暖方式造成了雾霾天气, 同时还带来了垃圾堆积、煤气中毒、火灾隐患等问题[1]。近年来, 政府出台了一系列政策, 如“煤改气”“煤改电”等, 以解决上述问题。然而由于农村居住分散、基础设施落后等原因, 在一定程度上限制了煤改气的实施。煤改电是指以空气源热泵采暖机组、电采暖以及电锅炉供暖的方式, 代替传统燃煤锅炉供暖[2]。单独使用空气源热泵的供暖系统存在输配能耗较高、系统循环性能系数(Coefficient of Performance, COP)低、热泵机组和水泵启停控制不合理等问题[3]。
采用固体蓄热装置, 将晚上用电低谷时成本低廉的电能储存起来, 在白天用电高峰时放出, 同时用于居民的采暖。这样既可以有效缓解发电系统的供需矛盾, 又可以使用户利用峰谷差电价降低用电成本。目前, 固体蓄热装置已成为国内外学者研究的热点。张培亭等人[4]针对10 kW固体电蓄热装置的蓄热过程进行了实验研究。李鹏程等人[5]采用瞬态实验方法, 研究了3种排列角度(15°, 30°, 45°)下扰流孔波纹板蓄热元件的传热性能。毕树茂等人[6]利用CFX程序对带电热板的矩形通道进行了流固耦合传热模拟。徐德玺等人[7]运用有限元法, 对固体蓄热装置的蓄热过程进行了模拟, 得到了蓄热体在不同时刻的温度场, 发现蓄热体的热效率随着通孔直径的增大而降低。梁炬祥[8]采用数值分析与实验结合的方法, 研究了加热元件(矩形加热板、圆形加热板、加热管)、热导率及加热强度等因素对固体蓄热的影响。胡思科等人[9]对蓄热体建立了二维模型, 分析了蓄热体放热孔形以及孔数对蓄放热性能的影响。杨小平等人[10]对蓄热介质为蓄热球的蓄热装置进行了研究, 对其蓄热过程中流固传热温差的不同形成原因进行了理论分析。SOROUR M M[11]通过实验研究了小型固体蓄热单元(蓄热材料为石膏岩填充床)的工作性能。PRAVEEN B等人[12]研究了新型乙二醇/CuO复合固体相变材料在储热散热器中的传热性能。GARCIA E L等人[13]分析了初始温度均匀的混凝土蓄热系统的放热效率、放热时间以及存储成本, 研究了不同管径下蓄热体在层流和湍流状态下对流热阻和导热热阻的变化, 发现湍流状态下, 在蓄热材料中添加高导热材料可使其导热热阻降低一个数量级, 提高放热效率。李晶晶等人[14]用数值模拟的方法研究了在自然对流状态下, 开设的孔数和孔形对蓄热装置放热特性的影响。结果表明: 椭圆形孔道中心线及孔出口温度明显高于圆形孔道相应位置处的温度; 如果孔形相同, 孔中心温度会随着孔数的增多而升高; 孔中心空气流速会随着孔数的增多而减小, 与孔形无关。
综上所述, 固体蓄热装置的研究主要集中于蓄热性能方面, 对放热性能的研究较少, 然而其放热速率直接影响居民的舒适度及房间内温度的平稳程度。为此, 本文根据GB 50736—2012《民用建筑供暖通风与空气调节设计规范》[15]与ASTM-C16.30标准[16], 设计了蓄热装置, 利用数值模拟方法, 研究了在蓄热体体积相同的情况下, 不同蓄热体结构对固体蓄热装置放热特性的影响, 以期为固体蓄热装置的使用提供参考。
1 固体蓄热装置放热特性模型建立
1.1 物理模型
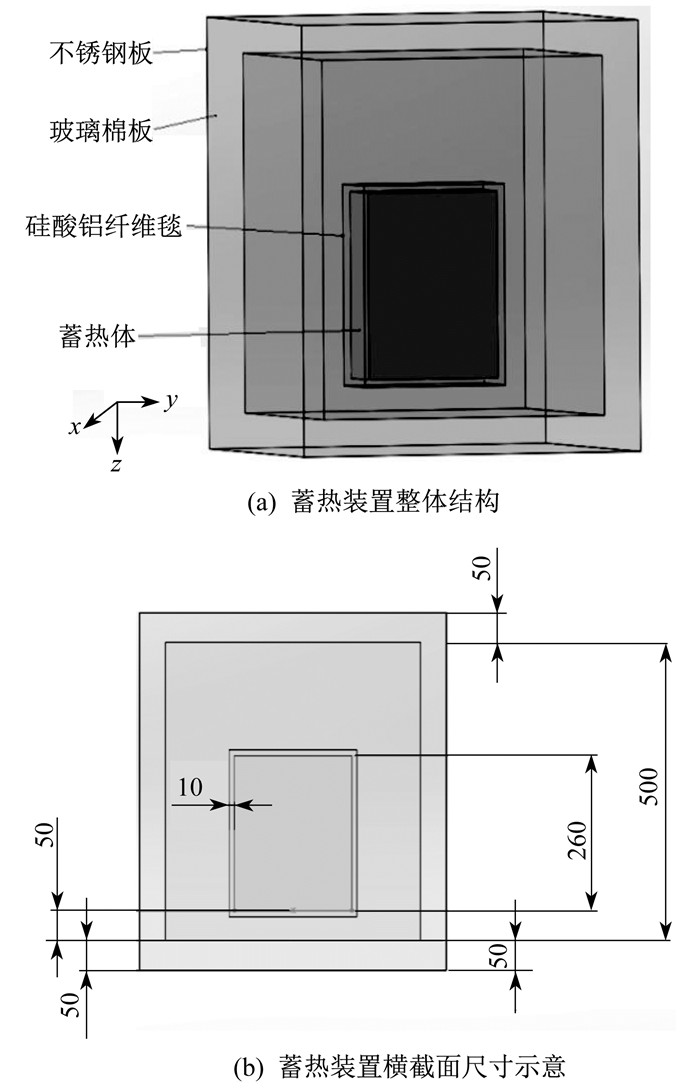
文献[17]中实验所用的蓄热体(S型蓄热体)由4块标准高铝砖砌成, 其中蓄热体的总体尺寸为230 mm×114 mm×260 mm, 保温层厚度为10 mm, 保温材料为硅酸铝纤维毯。正方体箱体边长为500 mm, 在厚度方向上分为3层, 从外到内分别是10 mm厚的不锈钢、50 mm厚的玻璃棉板和10 mm厚的不锈钢, 蓄热体距侧面100 mm, 距底面50 mm的位置。用Solid Works软件建立蓄热装置的三维模型, 如图 1所示。
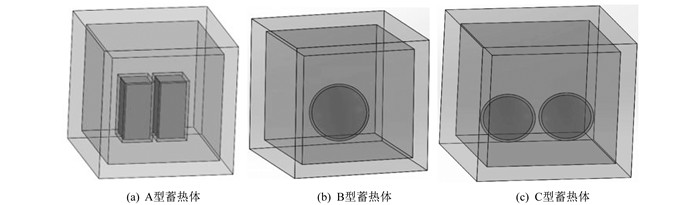
为了研究在蓄热体体积相同的情况下, 不同蓄热体结构对固体蓄热装置放热特性的影响, 根据文献[15-16]设计蓄热模型尺寸如下: 第1种蓄热体为2块长方体实心(A型)蓄热体, 长方体尺寸均为115 mm×114 mm×260 mm, 2块蓄热体关于x方向中垂面对称, 距离为40 mm, 底面距正方体框内底面均为50 mm; 第2种蓄热体为1块球形(B型)实心蓄热体, 球半径为117.63 mm, 球体关于x方向中垂面对称, 球心在正方体框内底面中心的正上方167.63 mm处; 第3种蓄热体为2块球形实心(C型)蓄热体, 球半径均为93.36 mm, C型蓄热体关于x方向中垂面对称, 球心距离为226.72 mm。
用Solid Works软件建立上述3种蓄热装置三维模型, 如图 2所示。4种材料的物性参数如表 1所示。
表 1
4种材料物性参数
| 材料名称 | 密度/(kg·m-3) | 导热系数/[W·(m·K)-1] | 比热容/[J·(kg·K)-1] |
| 高铝砖 | 2 400 | 0.500 | 1 000 |
| 硅酸铝纤维砖 | 120 | 0.126 | 1 340 |
| 玻璃棉板 | 80 | 0.050 | 1 220 |
| 不锈钢 | 7 930 | 20.000 | 480 |
1.2 数学模型
固体蓄热装置的实际传热是包含热传导、热对流和热辐射的复杂过程。为了分析影响研究对象运行特性的主要因素, 使得计算更加简便, 需要对研究模型进行合理简化, 并作出如下假设: 蓄热高铝砖是一种固态导热介质, 内部是均匀且连续的, 因此将内部的蓄热砖结构简化为长、宽、高固定的立体结构; 蓄热材料采用基于平均温度下的导热系数值。根据蓄热装置的结构, 分3部分建立数学模型。
1.2.1 空气流动区域控制方程
连续性方程为
| $ \frac{\partial \rho}{\partial t}+\frac{\partial \rho \boldsymbol{u}}{\partial x}+\frac{\partial \rho \boldsymbol{v}}{\partial y}+\frac{\partial \rho \boldsymbol{w}}{\partial z}=0 $ | (1) |
式中: ρ——密度;
t——时间;
u, v, w——x, y, z方向上的速度矢量。
动量方程为
| $ \frac{\partial \rho \boldsymbol{u}}{\partial t}+\operatorname{div}(\rho \boldsymbol{u} \boldsymbol{u})=-\frac{\partial p}{\partial x}+\frac{\partial \tau_{x x}}{\partial x}+\frac{\partial \tau_{y x}}{\partial y}+\frac{\partial \tau_{z x}}{\partial z} $ | (2) |
| $ \frac{\partial \rho \boldsymbol{v}}{\partial t}+\operatorname{div}(\rho \boldsymbol{v} \boldsymbol{u})=-\frac{\partial p}{\partial y}+\frac{\partial \tau_{x y}}{\partial x}+\frac{\partial \tau_{y y}}{\partial y}+\frac{\partial \tau_{z y}}{\partial z} $ | (3) |
| $ \begin{aligned} &\frac{\partial \rho \boldsymbol{w}}{\partial t}+\operatorname{div}(\rho \boldsymbol{w} \boldsymbol{u})= \\ &-\frac{\partial p}{\partial z}+\frac{\partial \tau_{z x}}{\partial x}+\frac{\partial \tau_{z y}}{\partial y}+\frac{\partial \tau_{z z}}{\partial z}-\rho g \end{aligned} $ | (4) |
式中: p——流体微元体上的压力;
τij——作用在微元体表面上的黏性应力τ的分量, i, j=x, y, z;
g——重力加速度, 。
能量方程为
| $ \frac{\partial \rho T}{\partial t}+\operatorname{div}(\rho \boldsymbol{u} T)=\operatorname{div}\left(\frac{\lambda}{C_{\mathrm{P}}} \operatorname{grad} T\right)+S_{\mathrm{T}} $ | (5) |
式中: T——热力学温度;
λ——流体的导热系数;
CP——比热容;
ST——黏性耗散量。
1.2.2 固体区域控制方程
固体区域的连续性方程和动量方向与空气流动区域相同, 能量方程为
| $ \frac{\partial \rho_{\mathrm{s}} h_{\mathrm{s}}}{\partial t}+\nabla\left(\rho_{\mathrm{s}} \boldsymbol{u}_{\mathrm{s}} h_{\mathrm{s}}\right)=\nabla\left(\lambda_{\mathrm{s}} \nabla T_{\mathrm{s}}\right)+S $ | (6) |
式中: ρs——蓄热体的密度;
hs——蓄热体的焓;
▽——梯度;
us——速度;
λs——蓄热体的导热系数;
Ts——蓄势体的温度;
S——源项。
1.2.3 流固耦合界面方程
由能量守恒定律可知, 在流固耦合交界面处, 蓄热砖释放的热量应该与空气吸收的热量相等, 公式表示为
| $ T_{\mathrm{s}}=T_{\mathrm{f}} $ | (7) |
| $ q_{\mathrm{s}}=-\lambda_{\mathrm{s}} \frac{\partial T_{\mathrm{s}}}{\partial \boldsymbol{n}}=-\lambda_{\mathrm{f}} \frac{\partial T_{\mathrm{f}}}{\partial \boldsymbol{n}}=q_{\mathrm{f}} $ | (8) |
式中: Tf, λf——空气的温度和导热系数;
qf, qs——空气侧和蓄热体侧的热流密度;
n——流-固交界面法向量。
1.3 网格划分
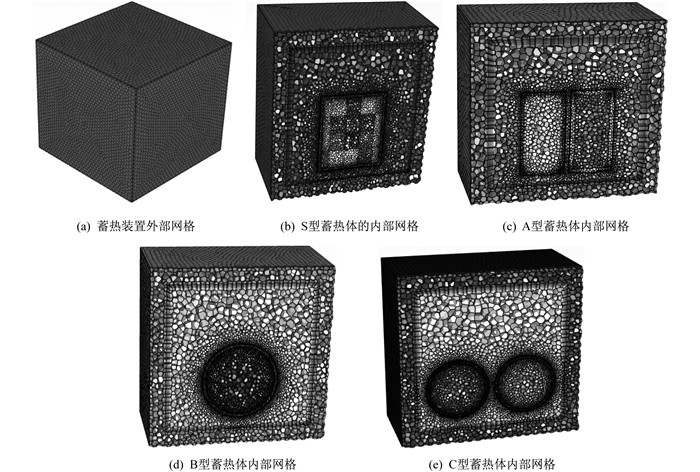
利用Fluent Meshing软件对4种蓄热体模型进行多面体网格划分, 如图 3所示。蓄热装置的放热过程是流固耦合传热的过程, 因此将流体区域与固体区域分离开, 以便在数值模拟计算时设置边界条件。数据通过流固耦合界面直接传递。网格质量和网格扭曲度均满足计算要求。
1.4 数值模拟条件及参数设定
采用Fluent软件进行模拟计算, 选用压力耦合求解器, 模拟时间为20 000 s。蓄热装置内空气流动属于湍流流动。由于realizable k-epsilon模型是非常流行的两方程模型, 具有可靠、收敛性好、内存需求低等优点, 因此本文采用该模型。
选用可放缩壁面函数来处理近壁面的区域。考虑辐射换热, 其模型为表面辐射(Surface to Surfaue, S2S)模型, 适用于在没有参与性介质的封闭空间内的辐射换热计算。在3 500 s时刻开启S2S模型。算法选用Simple算法。
具体模拟条件设置如下。
(1) 初始条件蓄热体初温为300 ℃, 房间空气初始温度为20 ℃。
(2) 边界条件正方体外壁温度为-5 ℃, 内壁和蓄热体(包含保温层)外表面均与空气耦合。
(3) 残差标准连续性方程、动量方程及能量方程收敛残差分别设为10-3, 10-6, 10-8。
2 数值模拟结果与对比分析
2.1 S型蓄热体实验结果与数值模拟结果对比
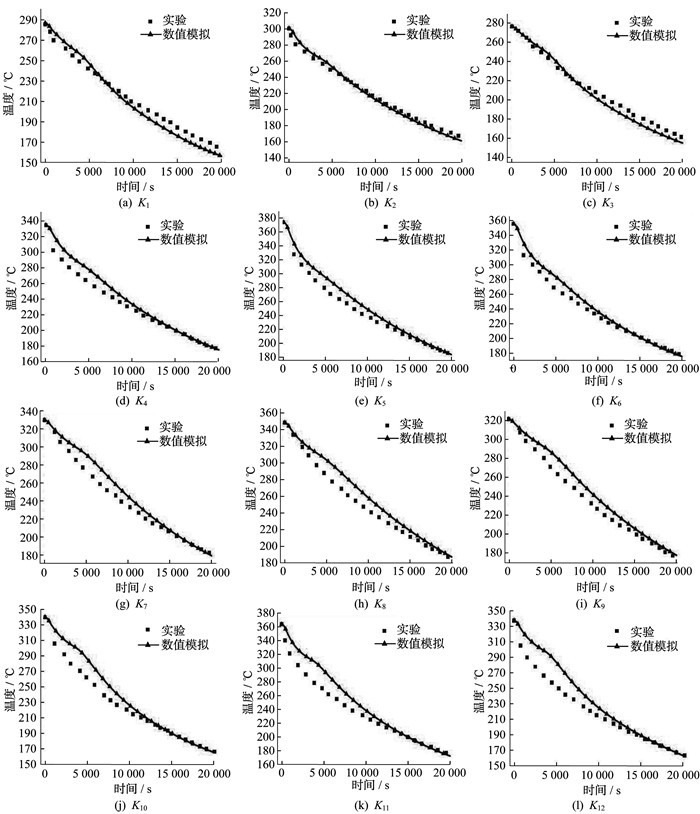
在S型蓄热体宽边方向的中垂面上, 沿着蓄热体的x方向和z方向设置12个温度监测点K1~K12。实验中, 在蓄热体的12个温度监测点使用镍铬-镍硅K型热电偶进行测温。测温结果与数值模拟结果如图 4所示。
从图 4可以看出, 在实验和数值模拟计算的情况下, 蓄热体上12个监测点的温度都会随着时间的延长而降低, 变化趋势相同。在模拟的前期与实验数据有一定误差, 计算后期差距很小。这是由于在模拟计算中, 初始条件只给了蓄热体一个初始温度300 ℃, 周围流体温度设定为20 ℃, 而蓄热体周围的空气温度实际上是随着蓄热体温度的升高而升高的, 不会是常温, 但具体的温度场是未知的, 在初始条件中无法给出; 而且正方体框内空气的流场有一定的流速, 不是绝对静止的, 但具体的流速大小是未知的, 在初始条件中无法给出的。因此, 前期模拟结果与实验数据有一定差距, 但所有温度监测点的相对误差都在5%以下。随着放热过程的进行, 所有监测点数值模拟得出的曲线斜率与实验得出的曲线斜率差距越来越小, 到后期几乎完全相同。这一结果验证了模型的正确性。
2.2 不同结构的固体蓄热装置放热特性的数值模拟结果分析
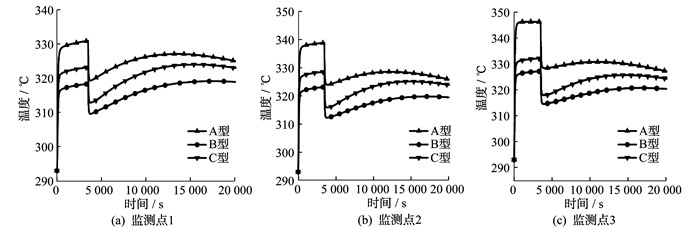
在3种不同结构的蓄热体中同一空间位置的监测点进行测温, 温度随时间变化的曲线如图 5所示。
3个监测点均位于y方向左右两侧的中垂面上, 监测点1在正方体框质心正前方157 mm处, 监测点2在监测点1的正上方150 mm处, 监测点3在监测点2的正上方150 mm处。
由图 5可以看出, 3种蓄热体的正方体框内温度变化规律基本相同。由图 5(a)可知, 在监测点1处3 500~20 000 s之间, B型蓄热体在约17 441 s达到最高值, A型蓄热体在约13 432 s达到最高值, C型蓄热体在约15 483 s达到最高值。由图 5(b)可知, 在监测点2处, B型蓄热体在约17 052 s达到最高值, A型蓄热体在约12 354 s达到最高值, C型蓄热体在约15 035 s达到最高值。由图 5(c)可知, 在监测点3处, B型蓄热体在约16 670 s达到最高值, A型蓄热体在约11 026 s达到最高值, C型蓄热体在约14 633 s达到最高值。说明A型蓄热体正方体框内的空气最先达到温度最高值, 其次是C型蓄热体,B型蓄热体的正方体框内的空气达到温度最高值所需时间最多。
由图 5还可以看出, 其次是C型蓄热体, B型蓄热体的正方体框内的空气温度变化曲线斜率最小, 说明温度最平稳, 从3 500 s开始温度逐渐升高, 当温度达到最高值后一直保持平稳状态; A型蓄热体和C型蓄热体的正方体框内空气温度变化规律相似, 都是从3 500 s开始, 空气温度开始升高, 达到最高值后开始缓慢下降。C型蓄热体的正方体框内空气温度变化曲线斜率大于A型蓄热体。在3 500~21 000 s之间, A型蓄热体所在正方体框内空气温度最高, 其次是C型蓄热体, B型蓄热体所在正方体框内空气温度最低。
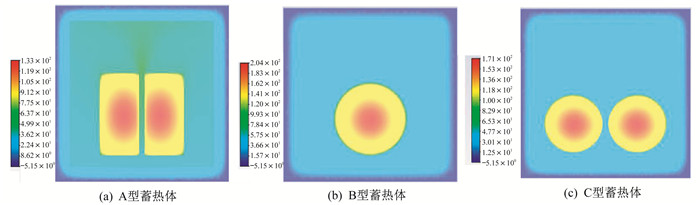
图 6是3种不同结构的蓄热体在20 000 s时刻的内部中垂面上的温度分布云图。
由图 6可以看出, 在20 000 s时刻, B型蓄热体的温度最高, 其次是C型蓄热体中每块蓄热体的温度, A型蓄热体中每块蓄热体的温度最低。在20 000 s时刻, A型蓄热体所在的正方体框内空气温度最高, 其次是C型蓄热体, B型蓄热体所在的正方体框内空气温度最低。这说明A型蓄热体的散热最快。
3 结论
(1) 在蓄热体总体积一定的情况下, A型蓄热体所在的正方体框内空气温度最高, 其次是C型蓄热体, B型蓄热体所在的正方体框内空气温度最低。
(2) 从3 500 s开始, A型蓄热体的正方体框内空气温度最先达到最高值, 其次是C型蓄热体, B型蓄热体的正方体框内空气达到温度最高值所需时间最多。
(3) B型蓄热体的正方体框内空气温度最平稳, A型蓄热体和C型蓄热体的正方体框内空气温度变化规律相似。C型蓄热体的正方体框内的空气温度变化曲线斜率大于A型蓄热体。
参考文献
-
[1]赵俊兰, 龚娴, 孙鹏程, 等. 我国北方农村地区的供暖形式比较[J]. 节能, 2019, 38(6): 161-164.
-
[2]李曾婷. "煤改电": 风生水起, 争议不断[J]. 电器, 2016(8): 24.
-
[3]刘子雄, 周恩泽, 濮延凯, 等. 北京地区"煤改电"供暖系统的分析与思考[J]. 山西建筑, 2017(25): 140-142.
-
[4]张培亭, 黄怡珉. 电热固体蓄热装置蓄热过程的实验研究[J]. 应用能源技术, 2004(6): 31-34. DOI:10.3969/j.issn.1009-3230.2004.06.013
-
[5]李鹏程, 孙志坚, 黄浩, 等. 扰流孔强化波纹板蓄热元件传热性能的实验研究[J]. 动力工程学报, 2016, 36(7): 530-534. DOI:10.3969/j.issn.1674-7607.2016.07.005
-
[6]毕树茂, 刘昌文. 矩形通道的流固耦合传热模拟[J]. 核动力工程, 2012, 33(2): 78-82. DOI:10.3969/j.issn.0258-0926.2012.02.017
-
[7]徐德玺, 金映丽, 邢作霞, 等. 基于有限元的固体电蓄热装置蓄热模拟及实验[J]. 机械工程与自动化, 2016(4): 23-25. DOI:10.3969/j.issn.1672-6413.2016.04.009
-
[8]梁炬祥. 固体蓄热传热过程的模拟分析及实验研究[D]. 合肥: 合肥工业大学, 2017.
-
[9]胡思科, 周林林, 邢姣娇. 圆形和椭圆形孔道固体蓄热装置蓄放热特性模拟[J]. 热力发电, 2018, 47(1): 38-45.
-
[10]杨小平, 杨晓西, 左远志, 等. 高温填充床蓄热过程中流固传热温差分析[J]. 工程热物理学报, 2015, 36(4): 825-828.
-
[11]SOROUR M M. Performance of a small sensible heat energy storage unit[J]. Energy Conversion and Management, 1988, 28(3): 211-217. DOI:10.1016/0196-8904(88)90024-6
-
[12]PRAVEEN B, SURESH S. Experimental study on heat transfer performance of neopentyl glycol/CuO composite solid-solid PCM in TES based heat sink[J]. Engineering Science and Technology, an International Journal, 2018(21): 1086-1094.
-
[13]GARCIA E L, MITSOS A. Effect of heat transfer structures on thermoeconomic performance of solid thermal storage[J]. Energy, 2014, 68: 896-909. DOI:10.1016/j.energy.2014.02.015
-
[14]李晶晶, 李永光, 王治源, 等. 固体蓄热装置圆形和椭圆形孔自然对流放热特性的研究[J]. 上海电力学院学报, 2019, 35(6): 525-530.
-
[15]中国建筑科学研究院. 民用建筑供暖通风与空气调节设计规范: GB 50736—2012[S]. 北京: 中国建筑工业出版社, 2012: 17-33.
-
[16]FEUILLOLEY P, ISSANCHOU G. Greenhouse covering materials measurement and modelling of thermal properties using the hot box method, and condensation effects[J]. Journal of Agricultural Engineering Research, 1996, 65(2): 129-142. DOI:10.1006/jaer.1996.0085
-
[17]李晶晶. 固体蓄热式装置散热特性的数值模拟与实验研究[D]. 上海: 上海电力大学, 2019.