|
|
|
发布时间: 2022-06-25 |
计算机与信息科学 |
|
|
|
收稿日期: 2022-03-08
中图法分类号: TK228
文献标识码: A
文章编号: 2096-8299(2022)03-0280-07
|
摘要
针对目前预测算法的预测时间短和预警不及时等问题,采用极限学习机(ELM)算法,构建了时序预测模型,并通过最小二乘法拟合构建预测值斜率趋势,采用高斯混合聚类得到了动态安全趋势阈值,再结合预测斜率趋势和动态安全趋势阈值实现了斜率趋势预警。结果表明,相比于门控循环单元结构(GRU)神经网络等建模方法,ELM算法具有更好的预警能力,并且斜率趋势预警能够较早发现运行时异常变化,实现准确且及时的预警。
关键词
极限学习机预测; 高斯混合聚类; 动态安全趋势阈值; 斜率趋势预警
Abstract
This paper aims at the problems of short prediction time and untimely early warning of current prediction algorithms.By using Extreme Learning Machine (ELM) algorithm, it builds a time-series forecasting model and constructs a forecasted value slope trend by least squares fit, using Gaussian mixture clustering to obtain dynamic security trend thresholds, combining predicted slope trend and dynamic safety trend threshold to realize slope trend early warning.The results show that the ELM algorithm has better early warning ability than modeling methods such as GRU neural network, and the slope trend early warning can detect abnormal changes in runtime earlier, and achieve accurate and timely early warning.
Key words
extreme learning machine prediction; Gaussian mixture clustering; dynamic security trend thresholds; slope trend warning
随着工业4.0和数字孪生技术的应运而生, 通过状态智慧监控实时掌握设备运行状态已经成为流程工业的必要环节, 能对运行设备即将出现的异常情况提前作出准确预警, 及时隔离或者替换异常设备, 这对整个流程工业系统的安全性和经济性起到积极的作用。
当前基于时序大数据进行预警的方法研究有很多。文献[1-3]使用多元状态估计法, 基于大量的历史数据, 从其正常运行状态中构建历史记忆矩阵, 然后通过当前设备状态值与历史记忆矩阵进行相似度运算, 得出当前运行状态与正常运行范围之间的偏离度, 当偏离度超出一定阈值时设备报警。这种方法采用的是实时运行值, 因此无法通过预测未来状态来进行比较。经典的机器学习模型如支持向量机[4]、贝叶斯网络[5]、高斯过程[6]均能够被用于非线性的时序预测。为了提高其预测的准确率, 需对影响时序预测的不同因素进行综合考虑, 本质是利用了其强大的回归分析能力[7]。这些学习算法依赖于历史数据的支持, 能够学习到数据在时序上的非线性关系, 其预测效果往往比基于物理模型和数据模型的算法更好。
随着计算机运算能力的提升, 神经网络[8]以及深度神经网络模型, 例如循环神经网络、卷积神经网络(Convolutional Neural Networks, CNN)、长短期记忆(Long Short-Term Memory, LSTM)网络等也被广泛用于时序预测之中[9-11]。文献[12]采用CNN - LSTM模型对黄金价格进行预测。文献[13]提出采用随机森林法、极端随机树和梯度提升决策树集成的算法进行预测。文献[14]提出利用XGBoost与随机森林两种集成算法相结合进行预测。也可以是不同类别的模型混合, 如利用神经网络和小波变化的风电预测[15], 线性模型与非线性模型的组合[16]等。由于这些人工智能预测方法存在预测精度差、预测长度短以及运算时间长等缺点, 并且设备运行参数的阈值对于数据的异常变化趋势难以表述, 因此采用以上预测与常规运行阈值比较的预警方法导致不能及时预警以及预警不正确等问题, 未能满足实际现场状态预警所要求的快速性和准确性。
针对以上问题, 本文提出了一种双重趋势分析结合的预警方法, 即基于极限学习机(Extreme Learing Machine, ELM)模型预测趋势和根据预测值拟合构建的斜率趋势, 结合参数的历史正常趋势以及安全斜率趋势阈值, 实现状态趋势预警。本文采用的ELM模型预测趋势方法可以有效克服传统神经网络学习时间长、运算速度慢等问题, 进一步采用最小二乘法拟合预测趋势为斜率趋势函数, 通过与聚类法得到动态安全趋势阈值的比较, 确定预警状态。
1 状态趋势预警研究
1.1 基于ELM的状态预测方法
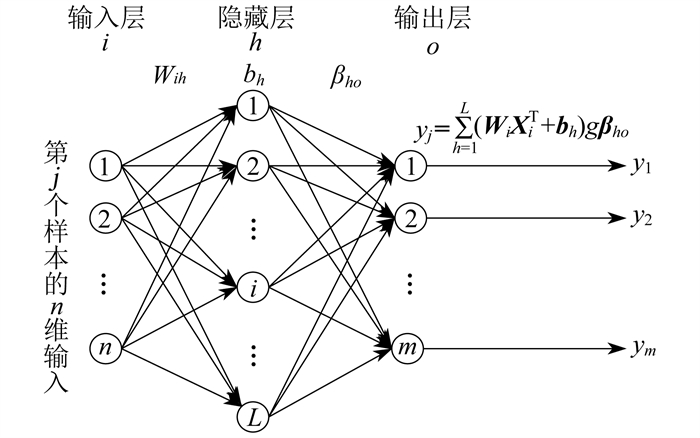
ELM是一种单隐层神经网络, 由一个输入层、一个隐藏层和一个输出层组成。其结构如图 1所示。
假设有N个样本(Xj, Yj), Xj为历史序列, Yj为预测序列, 预测周期为T。
每个样本输入层有n维, 隐藏层L维, 而输出层m维。其中: j=1, 2, 3, …, N, Xj=[xj1, xj2, xj3, …, xjn], Yj=[yj1, yj2, yj3, …, yjm]∈RN×m。一个单隐藏层神经网络的输出可以表示为
| $ {\mathit{\boldsymbol{Y}}_j} = \sum\limits_{h = 1}^L {\left( {{\mathit{\boldsymbol{W}}_i}\mathit{\boldsymbol{X}}_j^{\rm{T}} + {\mathit{\boldsymbol{b}}_h}} \right)} g{\mathit{\boldsymbol{\beta }}_{ho}} $ | (1) |
式中: Wi——输入权重, Wi=[w1h, w2h, w3h, …, wnh];
bh——第h个隐藏层单元的偏置, bh=[b1, b2, b3, …, bL];
g——激活函数;
βho——输出权重矩阵, βho=[β1, β2, β3, …, βL]T∈RL×m。
将式(1)写为矩阵形式, 即
| $ \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{\beta }}_{ho}} = {\mathit{\boldsymbol{Y}}_j} $ | (2) |
式中: H——隐藏层的输出矩阵。
其中, H, Yj, βho可分别表示为
| $ \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} {g\left( {{w_1}{x_1} + {b_1}} \right)}& \cdots &{g\left( {{w_L}{x_1} + {b_L}} \right)}\\ \vdots & \vdots & \vdots \\ {g\left( {{w_1}{x_N} + {b_1}} \right)}& \cdots &{g\left( {{w_L}{x_N} + {b_L}} \right)} \end{array}} \right] \in {R^{N \times L}} $ | (3) |
| $ {\mathit{\boldsymbol{Y}}_j} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Y}}_{11}}}& \cdots &{{\mathit{\boldsymbol{Y}}_{1m}}}\\ \vdots & \vdots & \vdots \\ {{\mathit{\boldsymbol{Y}}_{N1}}}& \cdots &{{\mathit{\boldsymbol{Y}}_{Nm}}} \end{array}} \right] \in {R^{N \times m}} $ | (4) |
| $ {\mathit{\boldsymbol{\beta }}_{ho}} = \left[ {\begin{array}{*{20}{c}} {{\beta _{11}}}& \cdots &{{\beta _{1m}}}\\ \vdots & \vdots & \vdots \\ {{\beta _{L1}}}& \cdots &{{\beta _{Lm}}} \end{array}} \right] \in {R^{L \times m}} $ | (5) |
当输入权重Wi和隐藏层偏置bh被随机确定为
| $ {\mathit{\boldsymbol{\beta }}_{ho}} = {\mathit{\boldsymbol{H}}^{\dagger} }{\mathit{\boldsymbol{Y}}_j} $ | (6) |
式中: H†——H的Moore-Penrose广义逆矩阵。
由于H∈RN×L, 而样本数N>>L, 故H†可表示为
| $ {\mathit{\boldsymbol{H}}^{\dagger} } = \mathit{\boldsymbol{V}}{\mathit{\boldsymbol{D}}^{\dagger} }{\mathit{\boldsymbol{U}}^{\rm{T}}} $ | (7) |
式中: U, V——相互正交的矩阵, U∈RN×N, V∈RL×L;
D†——主对角线为奇异值的对角矩阵D>非零元素取倒数再转置的矩阵, D∈RN×L。
其中, D, U, V可由矩阵H按奇异值分解得到, 即
| $ \mathit{\boldsymbol{H}} = \mathit{\boldsymbol{UD}}{\mathit{\boldsymbol{V}}^{\rm{T}}} $ | (8) |
其中, U由左奇异向量μi组成, V则是由右奇异向量vi组成, D则是主对角线为奇异值σi组成的对角矩阵。μi, vi, σi的计算公式分别为
| $ {\mathit{\boldsymbol{\mu }}_i} = \frac{1}{{{\mathit{\boldsymbol{\sigma }}_i}}}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{v}}_i} $ | (9) |
| $ \left( {{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H}}} \right){\mathit{\boldsymbol{v}}_i} = {\mathit{\boldsymbol{\lambda }}_i}{\mathit{\boldsymbol{v}}_i} $ | (10) |
| $ {\mathit{\boldsymbol{\sigma }}_i} = \sqrt {{\mathit{\boldsymbol{\lambda }}_i}} $ | (11) |
由于训练样本数N>>L, 矩阵H的行数远大于列数, 故Hβho=Yj为非一致方程, 对于使用Moore - Penrose广义逆矩阵求解超定问题(非一致方程), 其解βho为最小二乘最小范数解且唯一。
综上所述, ELM的训练步骤大致可分为3步:
(1) 为输入层和隐藏层之间的输入权重Wi和隐藏层偏置bh分配随机数值;
(2) 计算隐藏层的输出矩阵H;
(3) 求解非一致方程Hβho=Yj得出唯一的最小二乘最小范数解βho。
传统神经网络算法步骤分为: 提供数据给输入层神经元, 产生输出结果; 计算输出层误差, 计算输出层神经元梯度; 将误差逆传播至隐藏层神经元, 计算隐藏层神经元梯度; 更新连接权值与阈值; 反复迭代直到训练误差达到要求。
本文采用ELM模型, 基于前n个时间序列数据进行时间序列m步预测, 其预测周期为T。
1.2 基于最小二乘法拟合的状态趋势函数
基于ELM预测的m个点拟合状态趋势函数, 表示有限时间内的状态趋势变化。最小二乘法对当前预测与之前的预测结果进行线性拟合, 得到线性拟合函数y=at+b, 其中t=kT, T为预测周期。首先, 确定趋势函数的未知参数(通常是一个参数矩阵), 使得真实值与拟合值的误差et(也称残差)平方和最小。其损失函数E的计算公式为
| $ E = \sum\limits_{t = 1}^n {e_t^2} = \sum\limits_{t = 1}^n {{{\left( {{y_t} - y_t^\prime } \right)}^2}} $ | (12) |
式中: yt——真实值;
y′t——对应的拟合值。
要使损失函数最小, 可以将损失函数当作多元函数进行处理, 利用多元函数求偏导的思想计算函数的极小值。作为线性趋势函数, 损失函数可以写为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial f}}{{\partial a}} = \sum\limits_{t = 1}^n {\left[ {\left( {{y_t} - at - b} \right)t} \right]} = 0}\\ {\frac{{\partial f}}{{\partial b}} = \sum\limits_{t = 1}^n {\left( {{y_t} - at - b} \right)} = 0} \end{array}} \right. $ | (13) |
式(13)可变换为
| $ \left\{ {\begin{array}{*{20}{l}} {\sum\limits_{t = 1}^n t {y_t} - a\sum\limits_{t = 1}^n {{t^2}} - b\sum\limits_{t = 1}^n t = 0}\\ {\sum\limits_{t = 1}^n {{y_t}} - a\sum\limits_{t = 1}^n t - nb = 0} \end{array}} \right. $ | (14) |
联立上述两个多元方程组, 求解可得:
| $ \left\{ {\begin{array}{*{20}{l}} {a = \frac{{n\sum\limits_{t = 1}^n t {y_t} - \sum\limits_{t = 1}^n t \sum\limits_{t = 1}^n {{y_t}} }}{{n\sum\limits_{t = 1}^n {{t^2}} - \sum\limits_{t = 1}^n t \sum\limits_{t = 1}^n t }}}\\ {b = \frac{{\sum\limits_{t = 1}^n {{t^2}} \sum\limits_{t = 1}^n {{y_t}} - \sum\limits_{t = 1}^n t {y_t}\sum\limits_{t = 1}^n t }}{{n\sum\limits_{t = 1}^n {{t^2}} - \sum\limits_{t = 1}^n t \sum\limits_{t = 1}^n t }}} \end{array}} \right. $ | (15) |
依据式(15)求出线性拟合状态势函数, 采用单调函数直线y=at+b, 其中a为拟合函数的斜率, 代表了数据的趋势。若a>0, 则数据呈上升趋势; 若a < 0, 则数据呈下降趋势。结合基于正常历史时序的动态安全趋势阈值区间[Xl, Xh]进行预警。
1.3 基于聚类法的动态安全趋势阈值
采用高斯混合聚类法, 针对一组一维时序斜率趋势数据样本, 高斯混合模型假定所有的数据样本由k个高斯分布模型混合而成。其公式为
| $ P(x\mid \theta ) = \sum\limits_{i = 1}^k {{\omega _i}} P\left( {x\mid {\mu _i}, {\sigma _i}} \right) $ | (16) |
| $ \begin{array}{l} P\left( {x\mid {\mu _i}, {\sigma _i}} \right) = \\ \;\;\;\;\;\;\;\;\;\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}\sigma _i^2} }}\exp \left( { - \frac{{{{\left( {x - {\mu _i}} \right)}^2}}}{{2\sigma _i^2}}} \right) \end{array} $ | (17) |
式中: ωi——高斯分布模型之间的权重, 且满足
| $ {\omega _i} > 0, \sum\limits_{i = 1}^k {{\omega _i}} = 1; $ |
P(x|μi, σi)——高斯混合模型中的高斯分布模型;
μi, σi——第i个高斯分布的均值和方差, i=1, 2, 3, …, k。
高斯混合模型使用最大似然估计法估算参数的值, 公式为
| $ \begin{array}{c} L = \sum\limits_{j = 1}^N {\ln } P\left( {{x_{(j)}}\mid {\mu _i}, {\sigma _i}} \right) = \\ \sum\limits_{j = 1}^N {\ln } \left[ {\sum\limits_{i = 1}^k {{\omega _i}} P\left( {x\mid {\mu _i}, {\sigma _i}} \right)} \right] \end{array} $ | (18) |
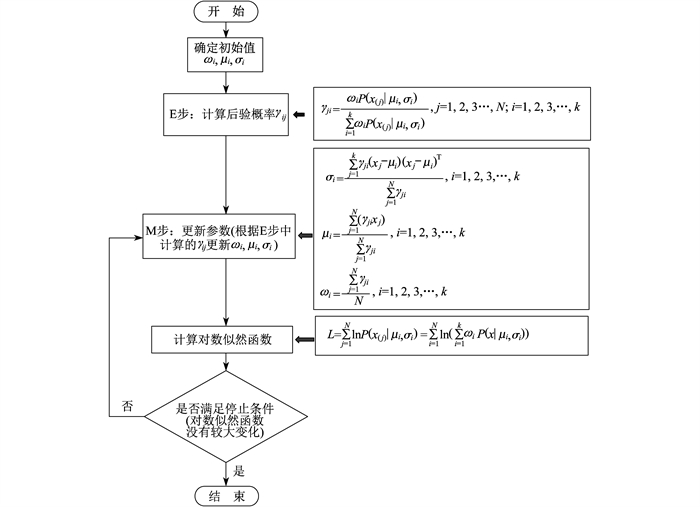
由于高斯混合模型内参数过多, 不能直接通过求导得出结果, 所以采用EM算法对模型进行迭代求解。EM算法求解流程如图 2所示。
通过EM算法求解出高斯混合模型的均值向量μi, 方差向量σi, 以及权重系数向量ωi, 则样本整体的均值为
| $ \bar x = \sum\limits_{i = 1}^k {{\mathit{\boldsymbol{\omega }}_i}} {\mathit{\boldsymbol{\mu }}_i} $ | (19) |
根据高斯概率分布函数的区间分布估计, 取95%置信度, 样本数据的上限向量Xhi与下限向量Xli的计算公式为
| $ {\mathit{\boldsymbol{X}}_{hi}} = {\mathit{\boldsymbol{\mu }}_i} + 1.96{\mathit{\boldsymbol{\sigma }}_i}\;\;\;\;(i = 1, 2, 3, \cdots , k) $ | (20) |
| $ {\mathit{\boldsymbol{X}}_{li}} = {\mathit{\boldsymbol{\mu }}_i} - 1.96{\mathit{\boldsymbol{\sigma }}_i}\;\;\;\;(i = 1, 2, 3, \cdots , k) $ | (21) |
样本整体的上限Xh与下限Xl为
| $ {X_h} = \max \left\{ {{\mathit{\boldsymbol{X}}_{hi}}(i = 1, 2, 3, \cdots , k)} \right\} $ | (22) |
| $ {X_l} = \min \left\{ {{\mathit{\boldsymbol{X}}_{li}}(i = 1, 2, 3, \cdots , k)} \right\} $ | (23) |
将动态安全趋势阈值区间[Xl, Xh]与当前状态趋势进行比较, 预警状态或发生于当前状态趋势斜率大于Xh或者小于Xl。
2 案例分析
2.1 模型预测及结果分析
本文对国内某电厂现场运行多组时序数据进行分析, 其中包含某真实故障运行状态数据, 采样间隔为30 s, 共500 000个数据, 部分数据如表 1所示。
表 1
历史运行数据
| 序号 | 磨煤机电流/A | 磨煤机出口压力/kPa | 磨煤机入口压力/kPa | 磨煤机入口风量/(t·h-1) | 磨煤机磨碗压差/kPa |
| 1 | 76.04 | 4.81 | 4.62 | 143.92 | 2.01 |
| 2 | 77.80 | 4.79 | 4.61 | 144.84 | 1.99 |
| 3 | 77.12 | 4.88 | 4.60 | 145.49 | 1.99 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 9 999 | 68.83 | 8.44 | 8.43 | 107.32 | 2.18 |
| 10 000 | 67.59 | 8.43 | 8.45 | 113.38 | 2.19 |
通过Python编程, 进行数据预处理。选取磨煤机电流经过数据预处理后的N=80 000个数据样本, 其中70 000个数据作为训练集, 剩余的数据作为测试集。ELM模型参数如表 2所示。
表 2
极限学习机模型参数
| 参数 | 数值 |
| 隐藏层维度L | 70 |
| 激活函数 | ‘tanh’ |
| 输入维度n | 40 |
| 输出维度m | 1 |
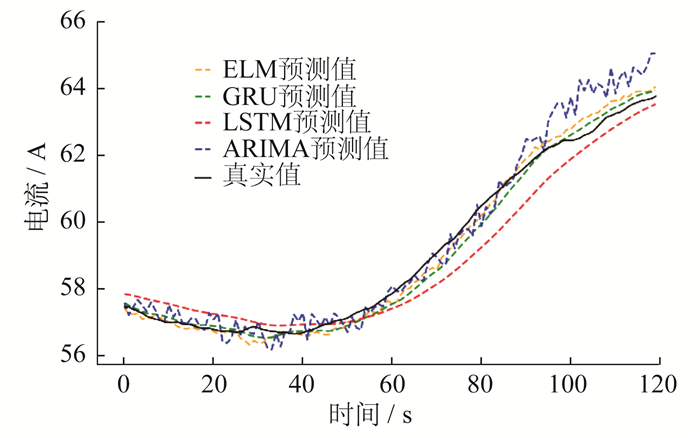
使用ELM模型与LSTM模型、门控循环单元结构(Gated Recurrent Unit, GRU)模型以及差分整合移动平均自回归(Auto Regressive Integated Moving Average, ARIMA)模型进行预测效果的对比。使用平均绝对百分比误差MAPE与决定系数R2作为预测模型的评价指标。各模型在测试集上的预测部分结果如图 3所示, 数据的采样间隔为30 s。
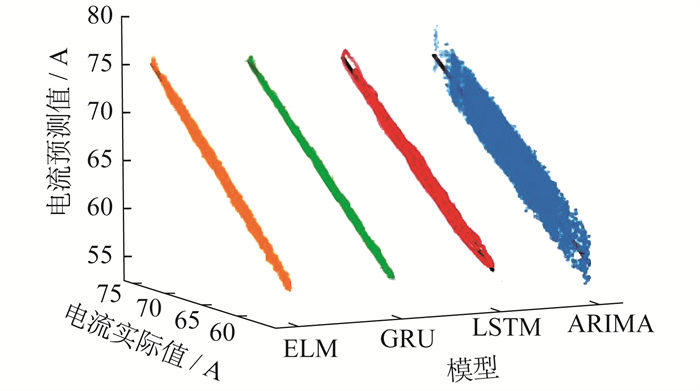
ELM模型与其他3种模型在同一数据集上的预测效果对比如图 4所示。由图 4可知, GRU模型的预测值最靠近理想直线, 预测效果最精确, ELM模型和LSTM模型的预测效果稍差于GRU模型, ARIMA模型的预测效果最差。
表 3为各模型的评价指标值和运算时间。由表 3可知, ELM模型的运算时间最短, 为1.6 s, ARIMA模型的运算时间最长, 为1 067.0 s。虽然ELM模型的预测效果稍差于GRU模型, 但是ELM模型在预测精度较高的条件下, 运算速度极快, 更加能够满足现场实时、即时的运行条件。
表 3
各模型的评价指标和运算时间
| 模型 | 评价指标 | ||
| MAPE/% | R2 | 模型运算时间/s | |
| ELM | 0.42 | 0.982 | 1.6 |
| GRU | 0.22 | 0.997 | 320.0 |
| LSTM | 0.45 | 0.973 | 340.0 |
| ARIMA | 1.99 | 0.844 | 1 067.0 |
2.2 预警结果及分析
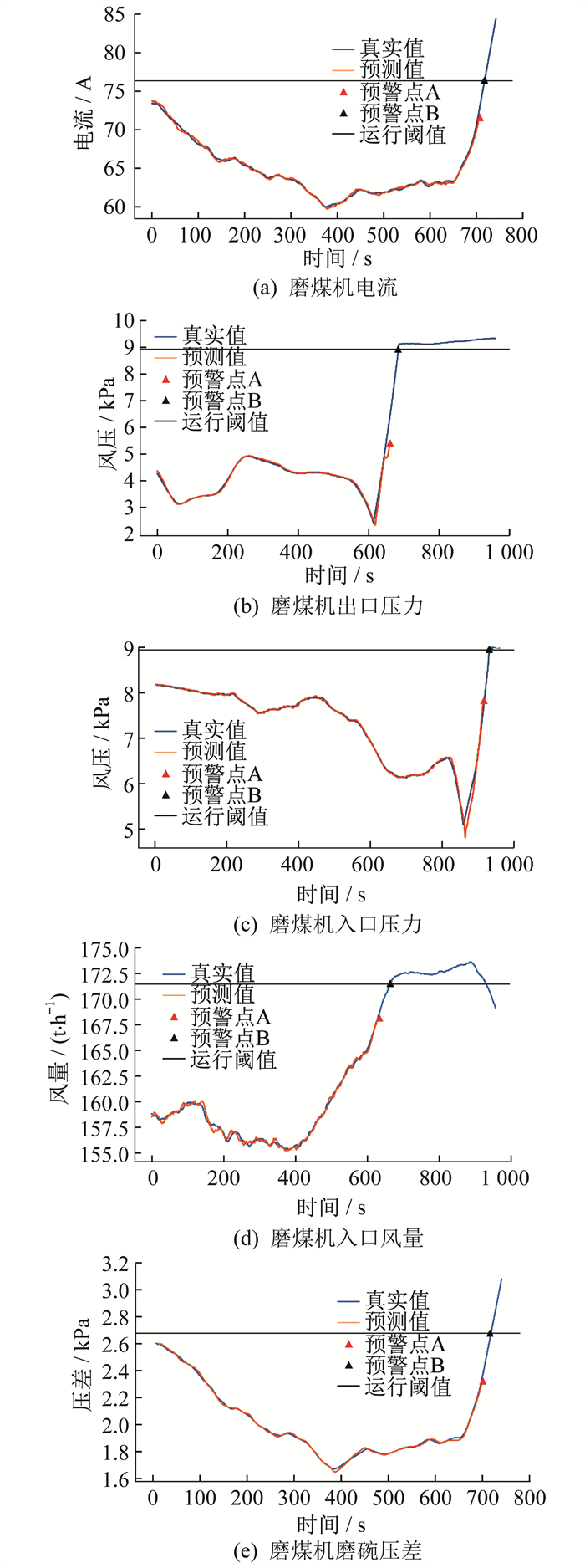
选取磨煤机电流、磨煤机入口压力等5组接近于故障状态的历史运行数据。首先利用最小二乘法对正常运行数据进行拟合得到斜率趋势样本D, 然后通过高斯混合聚类法得到各组正常运行数据的安全趋势阈区间[Xl, Xh], 最后通过本文的预警方法对运行状态进行判断。验证结果如图 5和表 4所示。
表 4
各组数据阈值以及提前预警时间
| 运行数据 | 运行阈值 | 斜率阈值Xh | 预警点A预测斜率 | 提前预警时间/s |
| 磨煤机电流 | 76.81 | 0.223 | 0.245 | 300 |
| 磨煤机出口压力 | 9.10 | 0.025 | 0.093 | 690 |
| 磨煤机入口压力 | 9.13 | 0.053 | 0.054 | 450 |
| 磨煤机入口风量 | 171.66 | 0.092 | 0.097 | 900 |
| 磨煤机磨碗压差 | 2.64 | 0.010 | 0.115 | 450 |
图 5中, 预警点A代表本文提出的预警方法所得到的预警点, 预警点B代表通过运行阈值比较所得到的预警点。由图 5可知, 预警点A的时刻均在预警点B之前。
由表 4可知, 预警点A处的预测斜率超过了安全趋势阈值。由对比结果可得, 本文所提预警方法的预警时间更早, 更加及时。
3 结语
本文提出了一种利用斜率趋势与动态安全趋势阈值相结合的预警方法, 利用ELM算法运算速度快且预测精度高的优点构建时序预测模型, 利用斜率趋势反映动态变化的优点结合动态安全趋势阈值构建预警模型。该预警模型相较于运行阈值预警能够较早发现异常变化的趋势, 克服了预警不及时的问题, 更加适合电厂实际运行中异常的及时发现。在后续工作中, 将对斜率趋势预警模型结合多维特征中的多时间尺度情况作进一步研究, 实现设备状态异常的早期发现。
参考文献
-
[1]滕卫明, 刘林, 卢伟明, 等. 基于SBM技术的发电设备故障预警系统研究[J]. 中国电力, 2015, 48(1): 40-46. DOI:10.3969/j.issn.1007-3361.2015.01.016
-
[2]常剑, 高明. 基于相似性建模的发电机组设备故障预警系统[J]. 机电工程, 2012, 29(5): 576-579. DOI:10.3969/j.issn.1001-4551.2012.05.020
-
[3]常志, 鲍克勤, 傅望安. 基于MSET的电厂引风机故障预警[J]. 上海电力大学学报, 2021, 37(2): 121-126. DOI:10.3969/j.issn.2096-8299.2021.02.004
-
[4]SAPANKEVYCH N I, SANKAR R. Time series prediction using support vector machines: a survey[J]. IEEE Computational Intelligence Magazine, 2009, 4(2): 24-38. DOI:10.1109/MCI.2009.932254
-
[5]XIAO Q K, CHU C Q, LI Z. Time series prediction using dynamic Bayesian network[J]. Optik, 2017, 135: 98-103. DOI:10.1016/j.ijleo.2017.01.073
-
[6]BRAHIM-BELHOUARI S, BERMAK A. Gaussian process for nonstationary time series prediction[J]. Computational Statistics & Data Analysis, 2004, 47(4): 705-712.
-
[7]杨海民, 潘志松, 白玮. 时间序列预测方法综述[J]. 计算机科学, 2019, 46(1): 21-28.
-
[8]蔡凯, 谭伦农, 李春林, 等. 时间序列与神经网络法相结合的短期风速预测[J]. 电网技术, 2008, 32(8): 82-85.
-
[9]ZHANG J, MAN K F. Time series prediction using RNN in multi-dimension embedding phase space[C]//SMG'98 Conference Proceedings. 1998 IEEE International Conference on Systems, Man, and Cybernetics. IEEE, 1998: 1868-1873.
-
[10]JAIN A K, GRUMBER C, GELHAUSEN P, et al. A toy model study for long-term terror event time series prediction with CNN[J]. European Journal for Security Research, 2020, 5: 289-309. DOI:10.1007/s41125-019-00061-w
-
[11]HUA Y X, ZHAO Z F, LI R P, et al. Deep learning with long short-term memory fortune series prediction[J]. IEEE Communications Magazine, 2019, 57(6): 114-119. DOI:10.1109/MCOM.2019.1800155
-
[12]LIVIERIS L E, PINTELAS E, PINTELAS P. A CNN-LSTM model for gold price time-series forecasting[J]. Neural Computing and Applications, 2020, 32: 17351-17360. DOI:10.1007/s00521-020-04867-x
-
[13]傅望安, 张泽发, 黄伟. 基于极端随机树的火电厂再热器故障预警算法研究[J]. 上海电力大学学报, 2020, 36(5): 445-450. DOI:10.3969/j.issn.2096-8299.2020.05.006
-
[14]丁婷婷, 杨明, 于一潇, 等. 基于误差修正的短期风电功率集成预测方法[J]. 高电压技术, 2022, 48(2): 488-496.
-
[15]CATALAN J P S, POUSINHO H M I, MENDES V M F. Short-term wind power forecasting in Portugal by neural networks and wavelet transform[J]. Renewable Energy, 2011, 36(4): 1245-1251. DOI:10.1016/j.renene.2010.09.016
-
[16]SHI J, GUO J, ZHENG S. Evaluation of hybrid forecasting approaches for wind speed and power generation time series[J]. Renewable and Sustainable Energy Reviews, 2012, 16(5): 3471-3480. DOI:10.1016/j.rser.2012.02.044