|
|
|
发布时间: 2022-08-25 |
清洁安全发电 |
|
|
|
收稿日期: 2021-12-15
中图法分类号: TL326
文献标识码: A
文章编号: 2096-8299(2022)04-0347-05
|
摘要
采用蒙特卡洛中子-光子(MCNP)输运程序构建了AP1000压水堆栅元模型, 进行典型燃料组件的栅格反应性模拟计算。研究了不同硼酸溶液浓度和水铀比下栅元的有效增值因数Keff值的变化规律, 得到了AP1000典型燃料组件的栅元反应性变化规律, 以期为核反应堆运行及设计提供数据参考。
关键词
AP1000栅元; 蒙特卡洛中子-光子输运程序; 硼酸溶液浓度; 水铀比; 有效增值因数
Abstract
The MCNP program is used to construct model of the AP1000 pressurized water reactor cell, and the grid reactivity simulation calculation of a typical fuel assembly is carried out.The change law of the effective multiplication factor Keff of the cell under different boron acid solution concentration and water-to-uranium ratios is studied, and the change law of the reactivity ρ of the typical AP1000 fuel cell is obtained to provide a data reference for the operation and design of nuclear reactors.
Key words
AP1000 cell; Monte Carlo neutron-photo transport code; boron acid solution concentration; water to uranium ratio; effective multiplication factor
随着我国经济的高速发展, 能源消耗量不断增长, 对开发和利用安全高效核电的需求也越来越迫切。“十四五”规划明确提出核电运行装机容量达到7 000万kW, 截至2020年底, 国内运行核电机组49台, 装机容量5 102万kW。在建机组16台, 在建总装机容量约1 738万kW。核电作为安全、清洁、低碳高能量密度的战略资源在“十四五”时期将迎来巨大发展[1]。
AP1000压水堆是第3代先进非能动型压水堆核电厂的核心装置, 同时也是具有高强度放射性的特殊部件。为了保证安全、可靠和经济地利用和发展核能, 一般通过模拟压水堆热态在不同条件下的工况, 达到真正安全使用核能的目的。有效增值因数Keff值是决定压水堆能否运行的重要参数, 由控制棒、硼酸质量分数和可燃毒物共同控制, 同时受到燃料芯块富集度、温度、水铀比等因素的影响。本文采用蒙特卡洛中子-光子(Monte Carlo Neutron and Photo, MCNP)输运程序软件构建AP1000压水堆栅元模型, 研究了硼酸溶液浓度和水铀比对有效增值因数Keff值的影响[2]。
1 压水堆反应性控制
目前, 压水堆均大多采用控制棒、固体可燃毒物和化学补偿控制(冷却剂中加入硼酸溶液)3种方式进行联合控制。其中, 化学补偿控制的价值约占53%, 其余为控制棒和固体可燃毒物所控制。因此, 化学补偿控制是压水堆核电厂反应性控制的重要方式之一[3]。为满足AP1000压水堆18个月的燃料循环时间, 在运行初期必须具有足够的剩余反应性, 启动后随时克服温度效应、中毒和燃耗引起的反应性变化。此外, 为使压水堆能够正常启动、停堆、提升或降低功率, 必须采用外部控制的方法来控制反应性[4]。
化学补偿控制只是用来补偿一些慢变化的反应性, 如慢化剂温度效应引起的反应性变化、裂变产物积累引起的反应性变化、平衡钐和平衡氙引起的反应性变化等。相比其他两种控制方式, 化学补偿控制方式加入的硼酸溶液在堆芯中分布更均匀; 不会引起压水堆功率畸变, 可以同步降低功率峰因子, 提高平均功率密度; 而且化学补偿控制具有不占用栅格位置、不使用驱动机构、简化反应堆结构等优势。
2 蒙特卡洛方法及MCNP程序
2.1 蒙特卡洛方法
蒙特卡洛方法, 又称随机抽样方法, 是一种与一般数值计算方法有本质区别的计算方法。它是利用随机数进行统计实验, 以求得的统计特征值(如均值、概率等)作为待解问题的数值解。与确定论方法不同, 实验统计方法不需要对某一特定的方程进行数值求解, 只需对研究问题构造一个随机模型并加以计算, 即可得到实验结果。使用蒙特卡洛方法时, 首先需要构造一系列的随机数对中子在介质中的运动轨迹进行模拟, 并追踪每个中子的历史, 最后对记录的数据信息进行加工就可以得到模拟结果。
蒙特卡洛方法适用于几何结构复杂或中子截面变化大的计算问题, 而且建模过程简单, 计算结果精确度较高, 是一种很有效的堆芯物理计算及屏蔽设计工具。随着现代计算机技术的飞速发展, 蒙特卡洛方法在原子弹工程研究中发挥了极其重要的作用, 已广泛应用于物理工程的各个方面, 如气体放电中的粒子输运过程等[5]。
2.2 MCNP输运程序
MCNP输运程序是由美国Los Alamos国家实验室应用理论物理部研究开发的。自1977年至今, 研究人员利用该程序解决了核能领域很多关键性问题, 其功能也越来越强大。目前, MCNP输运程序可在UNIX, LINUX, DOS, Windows 98, Windows XP等操作系统下工作。其最新版本MCNP-5可用于计算中子、光子、中子-光子耦合以及光-电子耦合的输运问题, 也可计算临界系统(包括次临界及超临界系统)的本征值问题。MCNP输运程序的应用范围十分广泛, 主要包括反应堆设计、核临界安全、辐射屏蔽和核防护、探测器的设计与分析、加速器靶的设计、医学物理与放射性治疗、国家防御、废物处理、射线探伤等[6]。
3 热态压水堆栅元模型的建立
3.1 几何描述
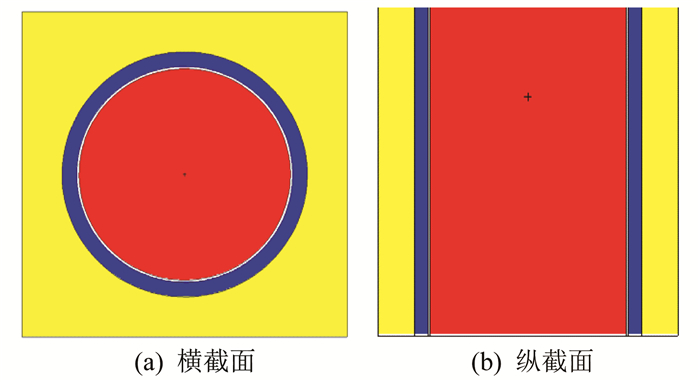
AP1000压水堆栅元结构的横截面和纵截面剖面图如图 1所示。
压水堆栅元尺寸如下: 栅距为1.26 cm; 轴向高度为2 cm; 燃料棒外径为0.819 15 cm; 锆合金包壳内径为0.835 66 cm, 外径为0.949 96 cm; 边界条件为栅元边界面是全反射条件, 等同无限栅元排布[7]。
慢化剂中的氢原子核对中子的慢化起主要作用, 因此慢化剂的用量会直接影响中子的生成数量。本文采用栅元内的慢化剂与燃料芯块的体积比作为水铀比, 其具体的计算公式如下[8]。
慢化剂与栅元的体积比为
| $ \frac{V_{\mathrm{M}}}{V_{\mathrm{PIN}}}=\frac{P^2-\frac{{\rm{ \mathsf{ π} }}}{4} D^2}{\frac{{\rm{ \mathsf{ π} }}}{4} D^2}=\frac{4}{{\rm{ \mathsf{ π} }}}\left(\frac{P}{D}\right)^2-1 $ | (1) |
式中: VM——慢化剂体积;
VPIN——栅元体积;
P——栅距;
D——燃料棒直径。
慢化剂与燃料芯块的体积比为
| $ \frac{V_{\mathrm{M}}}{V_{\mathrm{F}}}=\frac{V_{\mathrm{M}}}{V_{\mathrm{PIN}}} \cdot \frac{V_{\mathrm{PIN}}}{V_{\mathrm{F}}}=\left(\frac{V_{\mathrm{M}}}{V_{\mathrm{PIN}}}\right)\left(\frac{D}{d}\right)^2 $ | (2) |
式中: VF——燃料芯块体积;
d——燃料芯块直径。
栅元的几何参数主要是指燃料芯块的厚度、半径和栅距。本文保持燃料棒直径、燃料芯块直径、燃料密度、慢化剂密度不变, 通过改变栅距来实现水铀比的变化, 经过计算得到的结果如表 1所示。
表 1
不同水铀比对应的栅距
| 水铀比 | 栅距/mm | 水铀比 | 栅距/mm | |
| 0.5 | 9.86 | 3.5 | 15.97 | |
| 1.0 | 11.11 | 4.0 | 16.78 | |
| 1.5 | 12.24 | 5.0 | 18.28 | |
| 1.7 | 12.60 | 6.0 | 19.67 | |
| 2.0 | 13.27 | 7.0 | 20.97 | |
| 2.5 | 14.23 | 8.0 | 22.19 | |
| 3.0 | 15.13 |
3.2 材料描述
燃料棒的材料为UO2, 密度为10.466 8 g/cm3, AP1000压水堆中不同UO2富集度下各原子密度如表 2所示。其中, 原子密度的单位为1024个原子/cm3。本次模拟均采用富集度为3.40%的裂变材料[9]。
表 2
不同UO2富集度下的各原子密度
| UO2富集度/% | 原子密度 | ||
| U235 | U238 | O16 | |
| 2.35 | 5.555×10-4 | 2.279×10-2 | 4.669×10-2 |
| 3.40 | 8.037×10-4 | 2.254×10-2 | 4.670×10-2 |
| 4.45 | 1.051×10-3 | 2.230×10-2 | 4.670×10-2 |
锆合金包壳材料为ZIRLO, 密度为6.55 g/cm3。材料组分采用质量百分比为: Zr(锆)98.1%, Sn(锡)1.5%, Fe(铁)0.2%, Cr(铬)0.1%, O(氧)0.1%。
慢化剂材料为含硼水, 温度为290 ℃, 质量密度为0.746 051 522 3 g/cm3。不同浓度硼酸溶液(采用天然丰度的硼酸)对应的B10和B11的原子密度如表 3所示。
表 3
不同浓度硼酸溶液下B10和B11的原子密度
| 硼酸浓度/×10-6 | 原子密度 | |
| B10 | B11 | |
| 0(C0) | 0 | 0 |
| 200(C1) | 0.000 065 952 1 | 0.000 267 139 5 |
| 300(C2) | 0.000 098 938 1 | 0.000 400 749 3 |
| 400(C3) | 0.000 131 930 7 | 0.000 534 385 8 |
| 500(C4) | 0.000 164 929 8 | 0.000 668 049 1 |
| 700(C5) | 0.000 230 948 0 | 0.000 935 455 9 |
| 1 000(C6) | 0.000 330 024 8 | 0.001 336 766 9 |
| 1 300(C7) | 0.000 429 161 1 | 0.001 738 319 0 |
| 2 000(C8) | 0.000 660 710 9 | 0.002 676 212 7 |
4 实验结果与分析
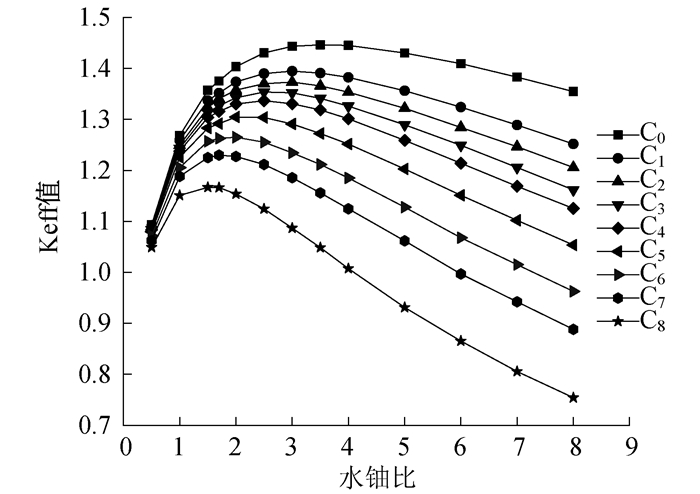
保持燃料富集度为3.40%, 改变硼酸溶液浓度和水铀比, 在MCNP输运程序中设置KCODE临界卡, 每次迭代中子数为5 000, 有效增值因数Keff值的初始尝试值为1, 累计计数前的非活跃代数为50, 迭代总次数为100次。记录实验中的Keff值, 结果如图 2所示。
在没有加入硼酸、水铀比为1.7时, 计算得出Keff值为1.337 21, 与文献[2]中压水堆总被控制价值为0.32基本一致, 同时栅元反应性模拟的相对误差控制在0.5%之内。
由图 2可以看出, 在水铀比相同、栅元栅距固定的条件下, 硼酸溶液的浓度越大, 栅元的Keff值越小, 反映了硼原子对中子的吸收效应。在硼酸溶液的浓度相同时, 随着水铀比的增大, Keff值都是先增加至最大值后开始减小。
图 2中, 曲线左侧为欠慢化区, 此时慢化剂水的比例降低, 抑制了中子的慢化, 使压水堆在较高的中子通量密度下运行, 这样的轻水堆称为欠慢化能谱反应堆; 右侧为过慢化区, 此时慢化剂的吸收效应占据主导地位。为了提高中子利用率, 设计压水堆时一般将水铀比设置在欠慢化区, 本文AP1000压水堆的水铀比为1.7。随着硼酸溶液浓度的增大, 欠慢化区与过慢化区的转折点向左移动。硼酸的加入提高了慢化剂的吸收性能, 使平衡过慢化倾斜, 因此转折点左移。硼酸溶液浓度为0~1.3×10-3时, 压水堆处于欠慢化区; 高于1.3×10-3后, 压水堆处于过慢化区。这也是核电站规定不能采用过高硼浓度(1.3×10-3~1.4×10-3)的原因之一。
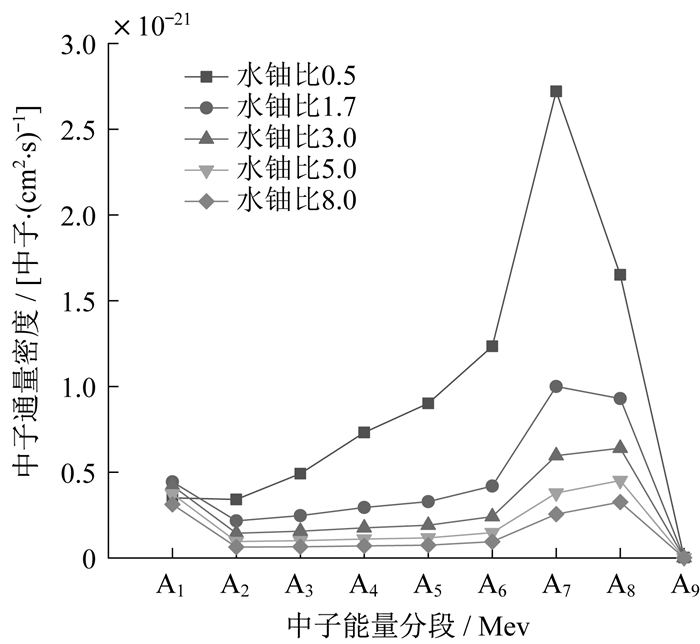
在上述基础设置上, 同时进行水铀比分别为0.5, 1.7, 3.0, 5.0, 8.0的5组能谱分析实验。使用En能量计数卡将中子按照0~1.0×10-6Mev(A1), 1.0×10-6~1.0×10-5Mev(A2), 1.0×10-5~1.0×10-4Mev(A3), 1.0×10-4~1.0×10-3Mev(A4), 1.0×10-3~1.0×10-2Mev(A5), 1.0×10-2~1.0×10-1Mev(A6), 1.0×10-1~1 Mev(A7), 1~10 Mev(A8), 10~20 Mev(A9)的分段进行划分[10], 记录各个能量分段的中子通量密度值, 结果如图 3所示。
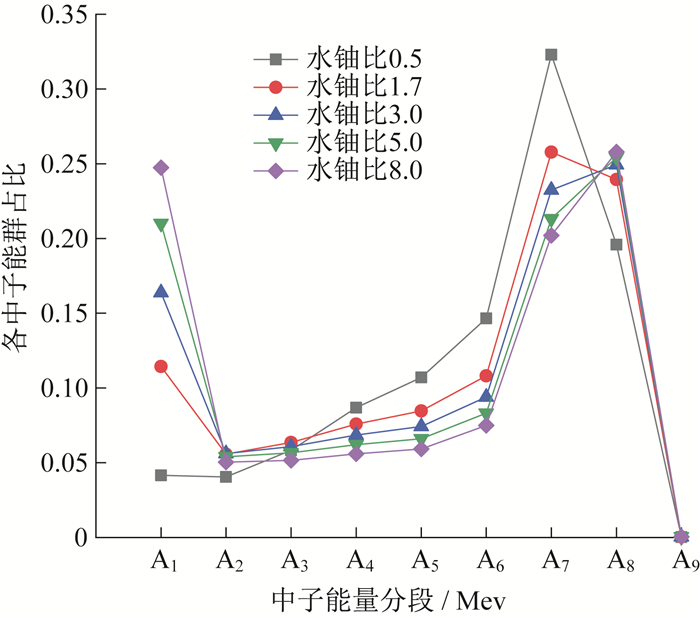
将各个能量分段的中子通量与总中子通量密度做比值, 计算结果如图 4所示。
由图 3可以看出, 随着水铀比的增加, 各个能量段的中子通量密度均有所降低, 中子通量密度最高的分段是1.0×10-1~1 Mev和1~10 Mev, 对应的压水堆裂变产生的中子能量平均值为2 Mev。这些中子通过与原子核发生弹性和非弹性碰撞, 使其能量降低至更容易引起下一次裂变的平均能量[11]。对于压水堆, 绝大多数中子被慢化成中能中子和热中子区域。由图 4可知, 随着水铀比的减小, 热中子减少, 快中子增加, 堆芯能谱变硬。由以上结果可知, 慢化剂与裂变材料UO2的相对比值对中子能谱分布起决定性作用[11]。
5 结论
本文利用MCNP输运程序构建了AP1000压水堆栅元的计算模型, 对压水堆有效增值因数Keff进行了模拟计算。
(1) 在不考虑控制棒和固体可燃毒物对反应堆Keff值的影响下, 随着硼酸溶液浓度的增大, 硼对中子的吸收效应增加, Keff值呈现线性降低。
(2) 随着水铀比的增大, 裂变中子能够得到有效慢化, 使得Keff值先逐渐增大至最大值, 然后由于慢化剂的吸收效应占据主导地位, 故Keff值随后逐渐降低。
(3) 随着水铀比的减小, 裂变产生中子慢化作用减弱, 热中子减少, 快中子增加, 堆芯能谱变硬。
(4) 慢化剂与裂变材料UO2的相对比值对中子能谱分布起决定性作用, 进而对压水堆Keff值造成影响, 因此压水堆设计中需要准确计算水铀比。
参考文献
-
[1]谢玮. "十四五"核电发展再迎新窗口[J]. 中国经济周刊, 2021(9): 68-70.
-
[2]谢仲生, 吴宏春, 张少泓. 核反应堆物理分析[M]. 西安: 西安交通大学出版社, 2004: 207-209.
-
[3]阎昌琪. 核反应堆工程[M]. 哈尔滨: 哈尔滨工程大学出版社, 2004: 115-119.
-
[4]孙汉虹, 程平东, 廖鸿兴. 第三代核电技术AP1000[M]. 北京: 中国电力出版社, 2016: 135-139.
-
[5]许淑艳. 蒙特卡洛方法在实验核物理中的应用[M]. 北京: 原子能出版社, 2006: 107-109.
-
[6]张建生, 蔡勇, 陈念年. MCNP程序研究进展[J]. 原子核物理评论, 2008(1): 48-51.
-
[7]刘建全, 石竟达, 张柳柳, 等. 基于MATLAB的AP1000核电机组反应堆DNBR特性研究[J]. 上海电力学院学报, 2015, 31(6): 505-510.
-
[8]于世和. 高燃耗压水堆堆芯物理特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
-
[9]DARNOWSKI P, IGNACZAK P, OBREBSKI P. Simulations of the AP1000-based reactor core with serpent computer code[J]. Archive of Mechanical Engineering, 2018(3): 295-325.
-
[10]陈德锋. 基于MCNP程序的AP1000反应堆屏蔽分析研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.
-
[11]于世和, 曹欣荣, 兰兵. 中子能谱对压水堆慢化剂温度系数的影响分析[J]. 原子能科学技术, 2013, 47(9): 1594-1598.